組合式螺旋槳重心誤差評價與修正

梁延德　孫捷夫　何福本　魯亞恒

大連理工大學,大連,116024

組合式螺旋槳重心誤差評價與修正

梁延德孫捷夫何福本魯亞恒

大連理工大學,大連,116024

由于槳葉在成形加工過程中受制造精度、材料缺陷及裝配誤差等非設計因素的影響，導致組合式螺旋槳的實際重心位置與理論設計重心位置不一致，對其力學性能會產生不良影響，因此需要對相關槳葉進行重心誤差評價和去重處理以修正重心誤差。提出了重心最小包容球和重心公差球的概念和算法，并以此為依據判斷槳葉是否需要進行重心修正。同時根據重心組合原理，分別以修正質量最小和槳葉重心離散程度最小為標準，提出了相應的修正方案，并利用理論分析和仿真實驗相結合的方法驗證了方案的可行性。

組合式螺旋槳;最小包容球;重心公差球;最小修正質量;重心離散程度

0　引言

組合式螺旋槳是由同種規格的多個槳葉通過焊接或鉚接的方式組裝而成的螺旋槳整體。槳葉的加工制造過程是先將鑄造好的槳葉毛坯件在普通機床上進行粗加工，然后通過數控機床進行精加工以及后期人工修整，但在實際制造過程中,由于存在加工精度以及裝配誤差等非設計因素，各個槳葉的實際重心在空間中位置并非一致[1],組合后螺旋槳重心偏離槳軸軸線，從而使得螺旋槳在轉動過程中產生較大的慣性力，使船舶在運行過程中加劇軸系同軸承間的振動和摩擦,導致軸系在加工制造過程中產生的內部微觀缺陷發展成宏觀裂紋，造成軸系的燒傷或斷裂，影響螺旋槳使用壽命。因此，在槳葉制造完成后，需要對其重心位置進行評價和相應的重心修正處理，以滿足設計指標和工作要求。

目前在槳葉重心評價方面的相關研究成果主要有:戈賁奇等[2]以螺旋槳葉片前端的不平衡質量為標準,對槳葉重心是否合格進行判定;謝偉[3]將傳統的掛重法進行改進，以螺旋槳靜平衡性能為標準，進行槳葉重心的評價。在實際工程中,對槳葉重心的修正主要依靠加工量估算和手工反復打磨，雖然該方法操作簡單、實施靈活，但加工質量難以保證。相關學者針對重心修正問題提出了一些改進方法：于穎等[4]根據槳葉曲面加工精度和公差的要求，應用計算機輔助工藝方法，求取加工過程中最小修正質量；李芳[5]通過圖像處理方法得出槳葉重心位置的偏差值,對槳葉進行打磨加工以修正重心；顧毅君等[6]以槳葉螺距誤差最小為目標，利用粒子群優化算法對螺旋槳加工量進行優化計算；曾艷等[7]針對槳葉毛坯的形狀誤差，利用改進的遺傳算法實現最優加工余量的計算。但目前尚未提出一種具有完整理論依據且計算效率高的重心誤差評價和重心修正方法。

本文針對組合式螺旋槳槳葉重心誤差評價問題，提出重心最小包容球和重心公差球的概念，判定是否需要對槳葉重心誤差進行修正，給出分別以最小修正質量和最小槳葉重心離散程度為評價標準的修正方案，最后利用ADAMS對組合式螺旋槳優化前后主軸力學性能進行仿真對比，驗證該重心評價和修正方案的有效性。

1　重心最小包容球

1.1最小閉包球概念

定義n維空間Rn是一個以c點為中心,以r(r>0)為半徑的球Bcr,可以表示為

Bcr={x∈Rn,‖x-c‖≤r}

(1)

其中,x表示空間Rn中任意一點,則‖x-c‖表示空間任意點距中心的Euclidean范數即距離范數。

在Rn空間中,設定其中m個點的集合為S={P1,P2,…,Pm},那么最小閉包球定義為能夠包含S中所有m個點且具有最小半徑的空間球[8]。

1.2重心最小包容球表式

對于組合式螺旋槳,每個槳葉的重心可以看作槳葉重心集合中的一點。理論上組合式螺旋槳各槳葉形狀完全一致，因而各個槳葉重心完全重合。實際上由于槳葉在成形加工過程中受制造精度、材料缺陷及裝配誤差等非設計因素的影響，組合式螺旋槳的實際重心位置與理論設計重心位置并不一致。

參考最小閉包球的概念可知，有且僅存在一個球域，半徑最小并能夠包含空間所有的重心點,該空間球域即為槳葉重心點的最小包容球。

如果設組合式螺旋槳由n個槳葉片組成,定義n個槳葉的重心坐標分別為C1(x1,y1,z1),C2(x2,y2,z2),…,Cn(xn,yn,zn),根據最小包容球的定義,重心最小包容球可表示為各個槳葉重心坐標的集合C={C1,C2,…,Cn}。

1.3重心最小包容球判定與槳葉最小包容球算法

在提出重心最小包容球概念后，如何確定螺旋槳槳葉的重心最小包容球仍需要詳細說明,但數學上的最小閉包球算法過于復雜,適用于大規模數據點的處理[9],而組合式螺旋槳一般由3到5個槳葉組成,因此本文僅針對組合式船槳提出槳葉重心的最小包容球判定準則與算法。

最小包容球的判定需要滿足以下兩個準則：①點集中所有點到最小包容球球心的距離小于等于最小包容球的半徑;②最小包容球邊界上的點所確定的最小包容球等價于原點集的最小包容球。

由最小包容球判定準則可知，在邊界點確定的情況之下，如果非邊界點都在邊界點所確定的最小包容球內部，則可確定點集的最小包容球即為該邊界點所確定的最小包容球，按照這種思想可以求解出點集的最小包容球。因此，根據常用組合式螺旋槳的槳葉數量分別就三葉槳、四葉槳以及五葉槳三種情況進行討論。

對于三葉槳,在槳葉空間中其重心連線為三角形，若三角形為銳角，作三角形的外接圓，以該外接圓為中截面作球，該球即為槳葉重心的最小包容球，如圖1a所示；若三角形為鈍角三角形或直角三角形，則以最長邊為直徑作球，該球即為重心最小包容球，如圖1b所示。

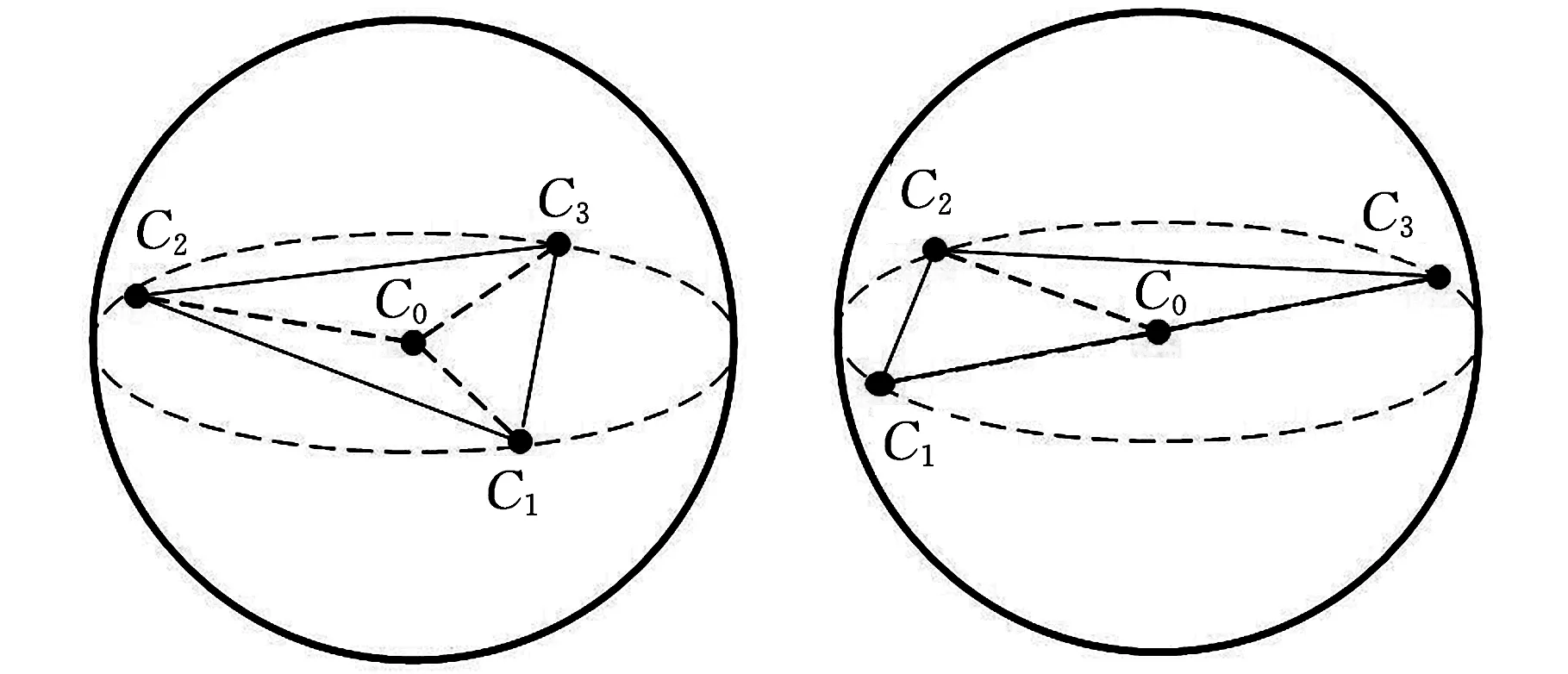
(a)銳角三角形重心連線(b)非銳角三角形重心連線圖1　三葉槳槳葉重心的最小包容球

對于四葉槳，在槳葉空間中其重心連線為四面體，作四面體的外接球。若球心在四面體的內部，則該外接球為槳葉重心的最小包容球，如圖2a所示；若球心在四面體的外部，則找到距離球心最近的四面體表面，過表面三角形作外接圓，以該外接圓為中截面作球，該球即為槳葉重心的最小包容球，如圖2b所示。

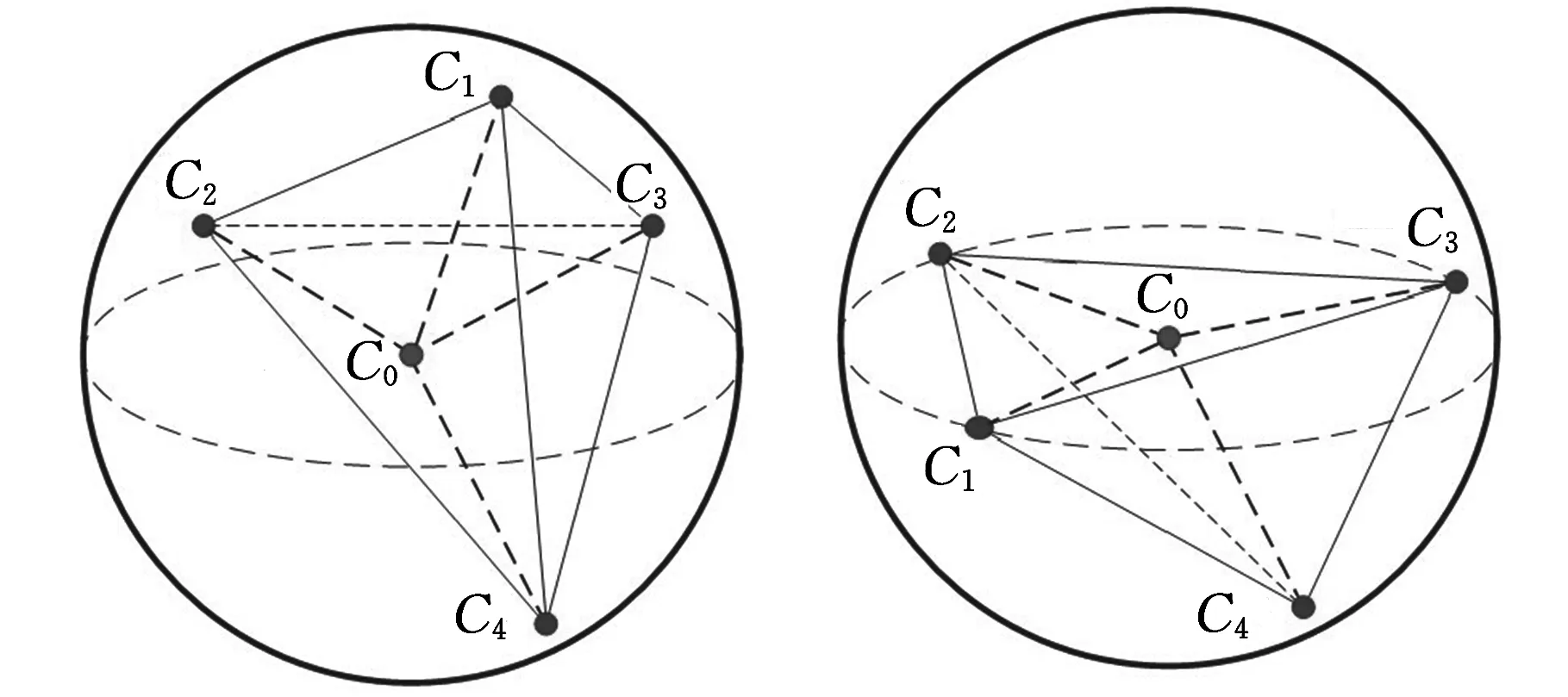
(a)重心在四面體內部(b)重心在四面體外部圖2　四葉槳槳葉重心的最小包容球

對于五葉槳，任選三個槳葉重心作其包容球，其組合數共有10種，再任選4個槳葉重心作其包容球，組合數共有5種。取滿足最小包容球判定原則①且半徑最小的包容球作為五葉槳重心的最小包容球。

為了驗證該算法的有效性,引入一組實際測得的四葉槳槳葉重心數據來求其重心最小包容球,如表1所示,經計算可以得到近似球心位置為C0(-47.154 mm,50.31 mm,685.27 mm),半徑R=1.206 mm。

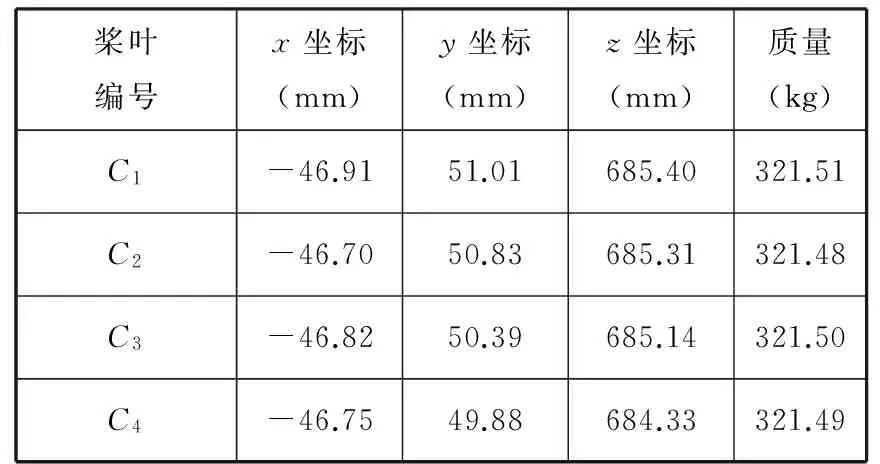
表1　槳葉重心坐標和質量

2　槳葉重心公差球

2.1重心公差球概念

由上文可知,組合式螺旋槳的各個槳葉的重心位置存在于重心最小包容球內。為了調整和優化螺旋槳的重心位置，需要對相關槳葉進行判定與修正，然而如何對槳葉重心進行評價仍需要進一步研究,因此本文提出槳葉重心公差球的概念。重心公差球是指能夠包容盡可能多槳葉重心點的空間球域,其半徑為在滿足性能需求時的最大半徑。

2.2槳葉重心評價準則

基于最小包容球和重心公差球的概念，可以將判定槳葉是否需要進行重心修正的準則描述為：當槳葉重心公差球半徑大于或等于最小包容球半徑時，槳葉合格，不需要對槳葉進行去重處理；當重心公差球半徑小于最小包容球半徑時，需要對螺旋槳槳葉進行修正,并且重心在重心公差球外的槳葉為需要重心修正的槳葉。

2.3重心公差球的確定

重心公差球的半徑為滿足性能需求時的最大半徑。在本問題中,半徑為0.1 mm。因此確定槳葉重心公差球的過程主要是確定其球心位置。具體操作步驟如下:

(1)確定基準槳葉。考慮到槳葉材料強度、水動力學性能等因素,槳葉的修正位置選擇為靠近葉梢的上半部分,因此以重心位置最低的槳葉作為修正基準槳葉,即不對此槳葉進行修正處理,將其槳葉重心位置標記為Cb(xb,yb,zb)。該槳葉重心點在重心公差球的內部。

(2)確定初始球心。以Cb(xb,yb,zb)為球心,以半徑r作空間球，則該球的描述方程為

(x-xb)2+(y-yb)2+(z-zb)2=r2

(2)

如圖3所示,過球心Cb沿著z軸正方向與球外表面的交點作為重心公差球的初始球心,記為Cq(xq,yq,zq)。

圖3　重心公差球球心算法示意圖

(3)確定重心公差球。考慮修正的槳葉越少,越節省資源，因此首先以需要修正槳葉數量最少的球為重心公差球。若存在多個球表明需要修正的槳葉的數量相同，則再以需要的修正質量之和最小的球作為最優重心公差球。為方便計算，將重心公差球球心以球坐標系形式表示。同時給出點(xq,yq,zq)的球坐標表達公式:

(3)

其中,α∈[-π/2,π/2]和β∈[0,2π]為設計變量,定義其初始值為α=π/2和β=0,考慮到計算機計算成本，設定-π/20為α的增量步長,π/20為β的增量步長,參考表1的數據,利用MATLAB編程,可以求得最優重心公差球的球心坐標為Cq(-46.75 mm,49.88 mm,684.43 mm)。

計算的最小包容球和重心公差球如圖4所示,C0為最小包容球球心,Cq為重心公差球球心,4個槳葉的重心坐標分別為C1、C2、C3和C4。由于重心公差球半徑小于最小包容球半徑,且槳葉重心C2不在重心公差球內，因此需要對C2所在的螺旋槳槳葉進行重量去除加工以修正重心。

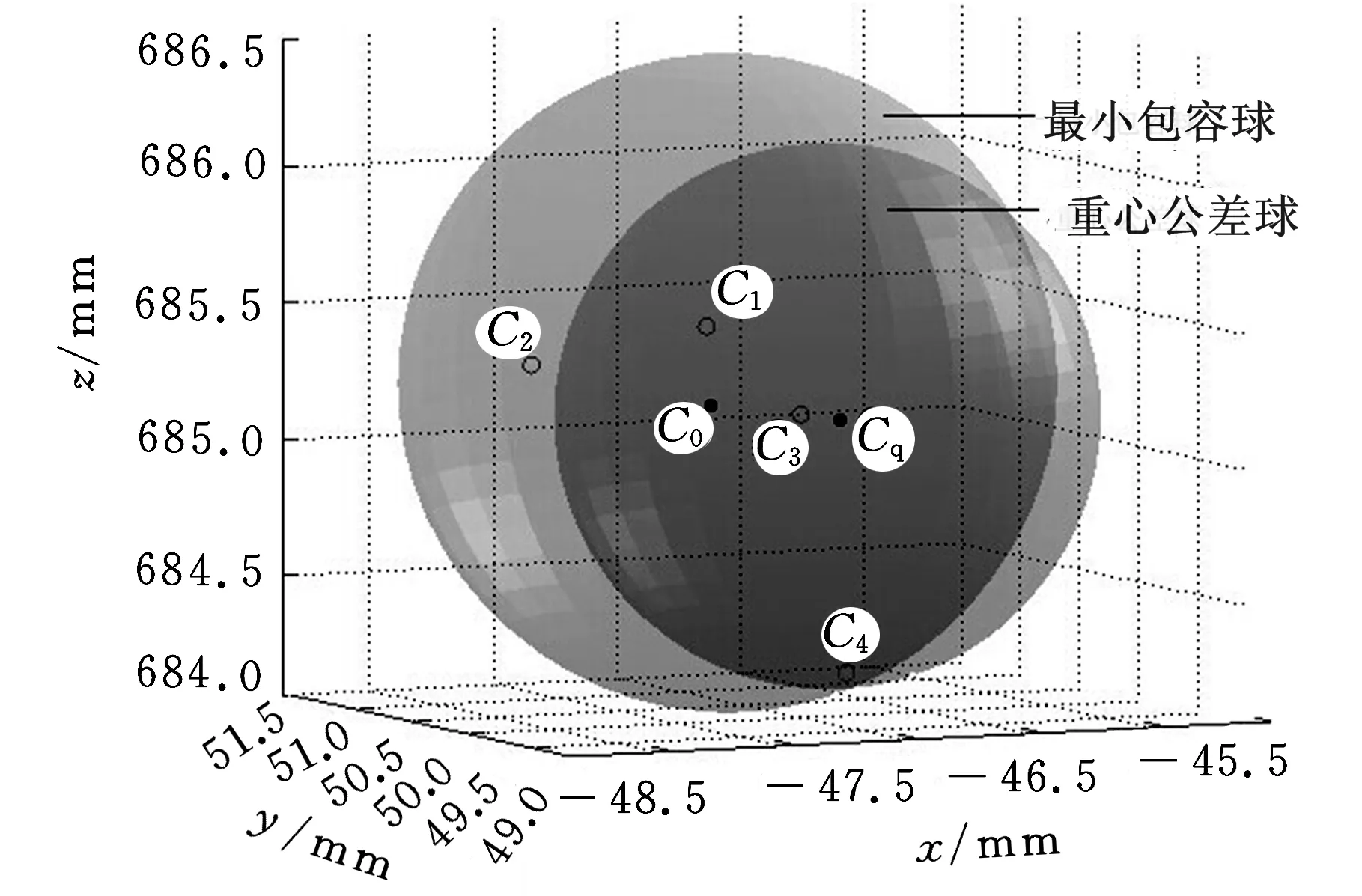
圖4　最小包容球和重心公差球

3　重心修正

3.1槳葉重心修正位置的確定

在確定需要進行重心修正的槳葉后,要確定槳葉的修正區域，要求在該區域進行重心修正后,可以使槳葉重心移動到重心公差球內，滿足使用要求。由于修正之后的槳葉重心滿足重心組合原理，即修正后槳葉的重心和槳葉上修正點合成的位置點為修正之前的槳葉重心。因此，由幾何知識可知，過不合格槳葉重心A，作重心公差球的外切圓錐，該圓錐的反向延長與槳葉的交線所圍成的區域即為槳葉的修正區域。過重心公差球之中的點B，向不合格槳葉重心方向作映射線，與槳葉表面的交點C即為對應的修正位置,如圖5所示。

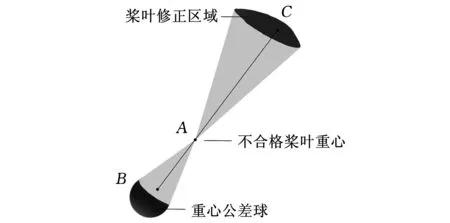
圖5　修正位置確定示意圖

3.2去除質量最小修正方案

在修正區域進行質量去除加工，可以使該槳葉重心移動到重心公差球內，滿足設計要求。考慮螺旋槳水動力性能因素，槳葉在修正加工之后，表面形狀相應發生改變，修正質量越大，槳葉表面形狀改變越大，對水動力性能影響越大，修正質量應該盡可能小，因此提出以最小修正質量為標準，確定槳葉上最優修正位置及修正質量。

設修正點到不合格槳葉重心的距離L1,不合格槳葉重心與重心公差球上對應點的距離L2,重心修正前不合格槳葉的質量為q,修正質量為Δq,根據重心組合原理,可知:

(q-Δq)L2=ΔqL1

(4)

求解式(4)可得：

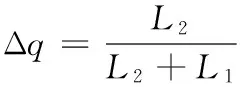
(5)

令a=L1/L2,根據式(5),可以求出在修正區域各點的修正質量,當修正質量Δq最小,即a取得最大值時,修正區域上對應的點為最優修正點。

3.3重心離散程度最小修正方案

在同一坐標系中,各槳葉的重心點離散程度越小，即可認為槳葉相似程度越高，則組裝之后的螺旋槳在轉動過程中的力學性能越好。因此不合格槳葉修正后的重心應該是在重心公差球內使所有槳葉重心離散程度最小的點。在數理統計中，常用描述數據離散程度的度量值有極差(全距)、平均絕對偏差和方差等，但極差容易受到數據極端值的影響，平均絕對偏差在數學處理上不方便，而方差不僅可以反映數據的離散程度又便于數學上的處理，因此選用方差評價各槳葉重心的離散程度。

設組合式螺旋槳由N個槳葉組成,當存在一個不合格槳葉時，設合格槳葉的重心坐標Ci(xi,yi,zi),i=1,2,…,N-1,不合格槳葉經過重心修正后的重心坐標為Ck(xk,yk,zk),則經過修正后的不合格槳葉的重心坐標到其他重心點坐的距離方差可表示為

(6)

式(6)是關于xk、yk、zk的二次曲線,圖形開口向上。其中，所有槳葉重心坐標的平均值為

(7)

當不合格槳葉重心修正后的重心坐標等于其他合格槳葉重心坐標的平均值時,方差取最小值,此時組合式螺旋槳的槳葉重心點離散程度最小,即

(8)

由于各種非設計因素的存在,組合式螺旋槳的各個槳葉的實際重量并不完全相同，因此在計算槳葉平均重心位置時需要考慮各個槳葉的重量wi,進行加權平均值的計算,加權平均值的算法為

(9)

基于上述推導可知,當不合格槳葉經過重心修正后,重心位于合格槳葉重心的加權平均值時,方差最小,各槳葉重心離散程度最小,此時該點為最優重心點。

將表1中各槳葉重心坐標和質量代入式(9)可計算出不合格槳葉的最優重心點坐標為(-47.01 mm,50.94 mm,685.5 mm)。

4　仿真驗證

4.1理論分析

在進行槳葉重心修正之前,由于不合格槳葉重心存在較大偏差,在安裝之后,螺旋槳的重心不在槳軸中心線上,螺旋槳在繞槳軸中心線旋轉過程中，合格槳葉產生的離心力合力大小為F1,不合格槳葉產生的離心力合力大小為F2，它們之間存在一個夾角αo,因而槳軸會產生一個偏心力,大小為FD,如圖6所示,FD的表達式為

(10)

E處和F處軸承會分別給槳軸提供相應的支承力,其大小分別為FE和FF,設EF段長l1,DE段長l2,則由力學平衡可知：

(11)

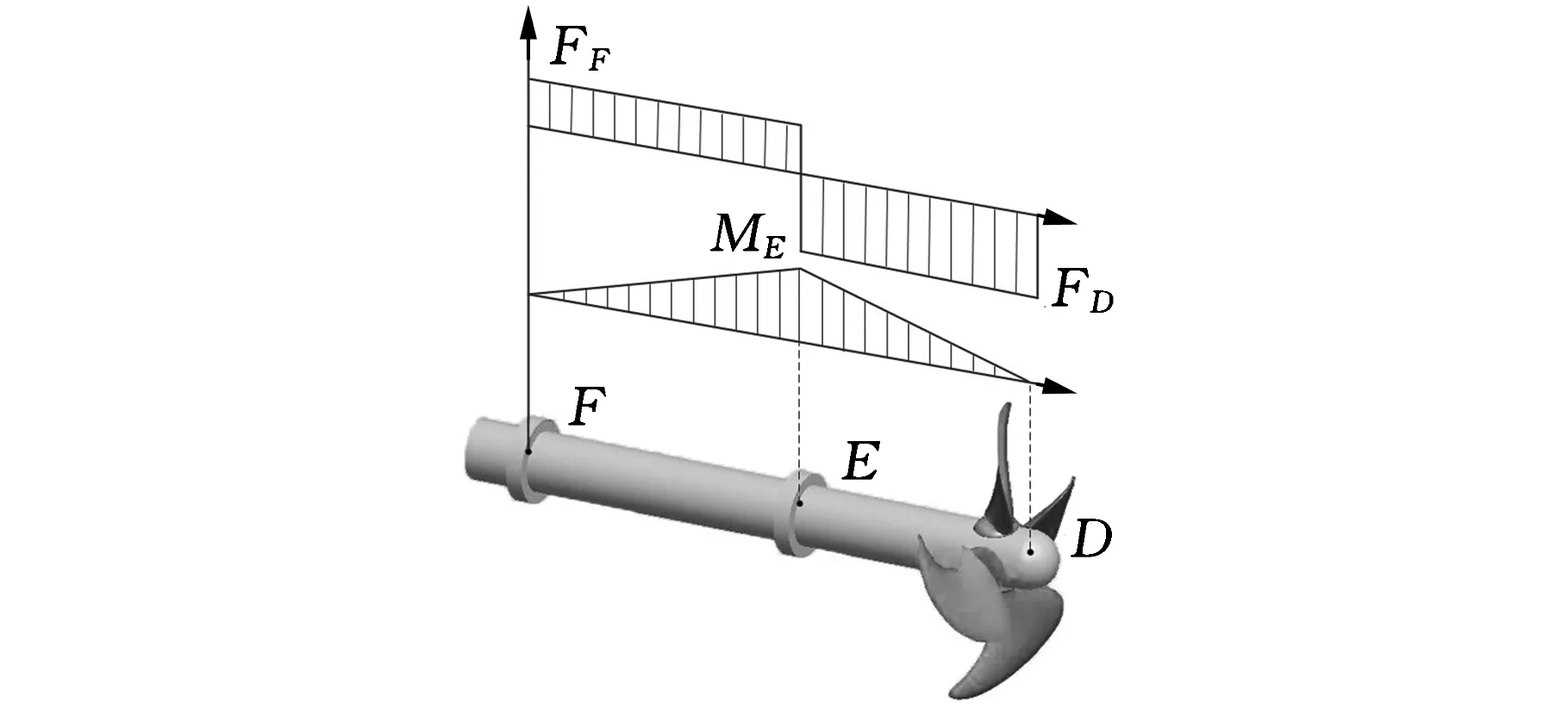
圖6　槳軸受剪力和彎矩圖

E處所受彎矩大小為

ME=FDl2

(12)

由圖6可以看出,槳軸的危險截面即在支承E處,因此對E截面進行力學分析與仿真,由式(9)可知,當不合格槳葉重心修正之后,各槳葉重心坐標更加接近,轉動時產生的離心力F1與F2大小趨于相等,夾角αo趨于180°,相應偏心力FD減小,進而截面E處受到剪力和彎矩均減小,螺旋槳力學性能得到改善。

4.2力學仿真驗證

在動力學分析軟件ADAMS的仿真環境中,剛體在受力情況下無法產生彈性變形[10],而實際工作情況中,槳軸的形變會引起質量分布的改變,槳軸的轉動和柔性槳軸的變形是相耦合的,因此,傳統的剛體動力學分析無法滿足要求,為了模擬實際工作情況，利用ADAMS中Flex模塊實現螺旋槳的剛柔耦合仿真分析。仿真中采用轉速為120r/min,額定轉矩為1.95×105N·m的永磁同步電機定轉速驅動,并設置仿真時間為30s,步長為3000。

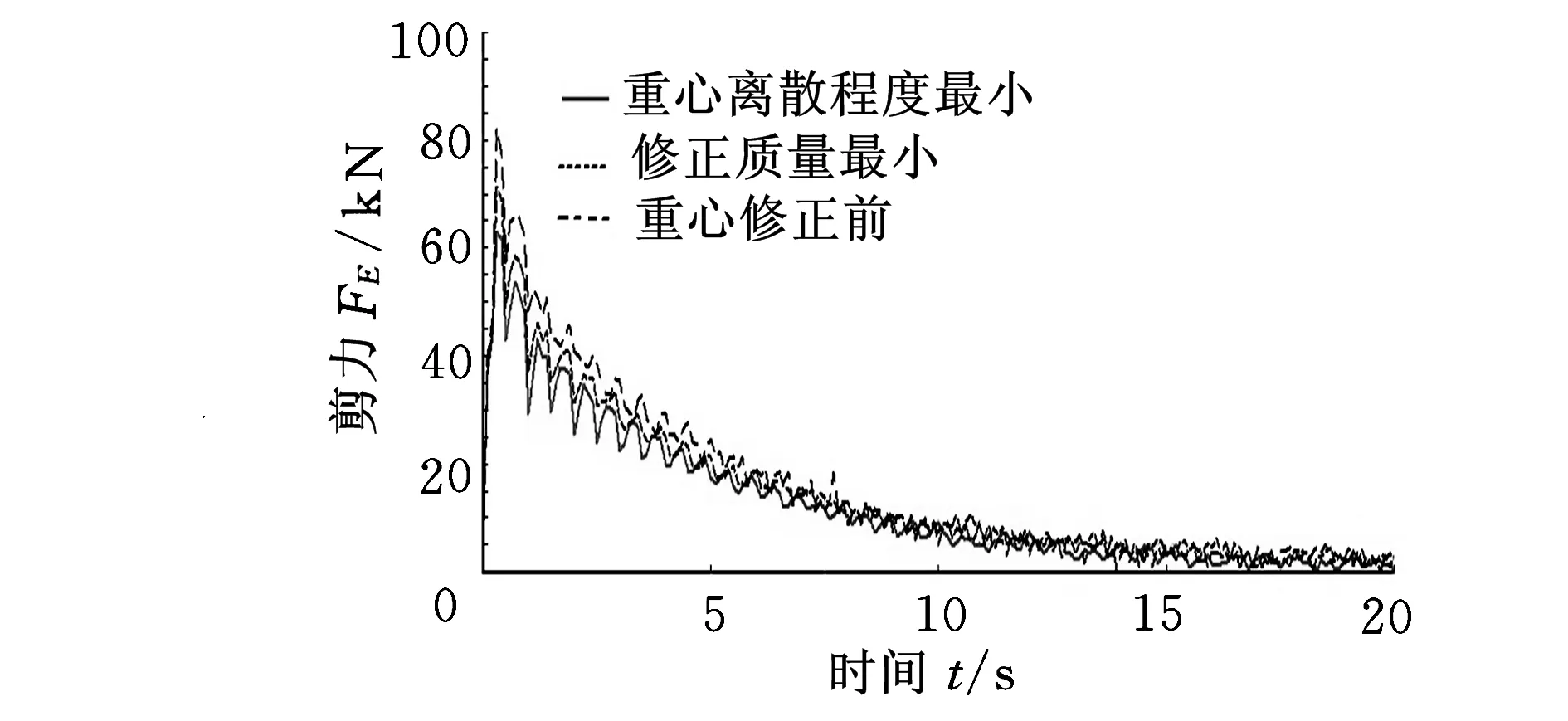
螺旋槳工作過程中,槳軸自由端變形最大,因此對其D處的徑向位移變化情況進行仿真分析,如圖7a所示;根據理論分析可知，槳軸的危險截面在后支承E處,因此以該截面作為仿真對象,對比螺旋槳重心修正前后受到剪力和彎矩變化情況,如圖7b和圖7c所示。

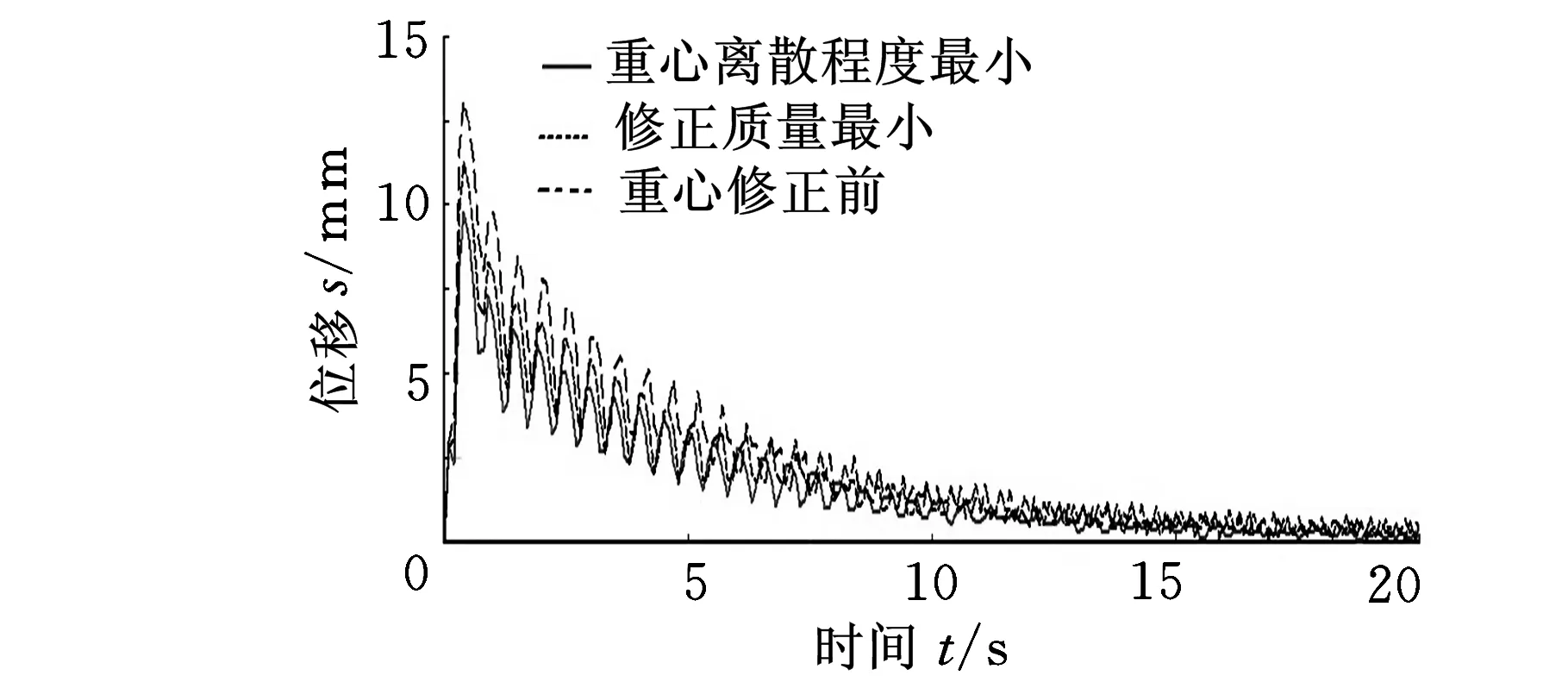
(a)位移變化曲線

(b)剪力變化曲線

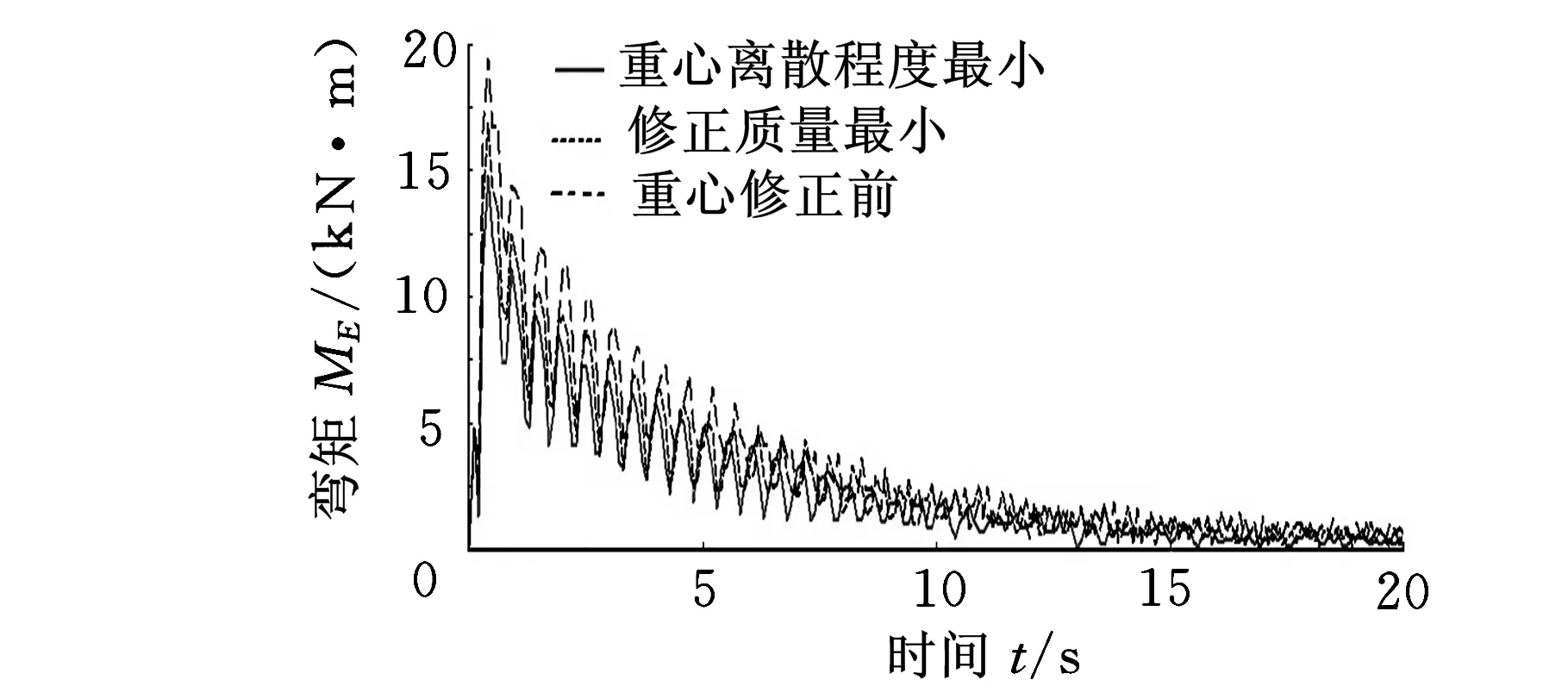
(c)彎矩變化曲線圖7　重心修正前后槳軸力學性能變化曲線

由圖7可知,位移曲線、受力曲線和彎矩曲線在剛啟動時有較大的波動，是因為仿真中施加定轉速驅動，軟件在仿真開始時需要設定系統初值，隨著時間的增長各曲線逐漸收斂，各曲線在穩定后仍有小幅度的波動,這是由柔性體在工作過程中的振顫引起的,與實際情況相符,仿真結果如表2所示。

由表2可知,經過兩種方案進行重心修正后槳軸危險截面處受力和力矩有較大的減小， 自由端振動情況也有不同程度的改善，其中重心離散程度最小方案效果更為明顯，危險截面處受剪力相對修正前減小了68.45%,所受彎矩減少了57.69%,延長了螺旋槳的使用壽命；自由端徑向位移相對修正前減少了63.10%,改善了螺旋槳的動平衡性能，減少了振動和噪聲。

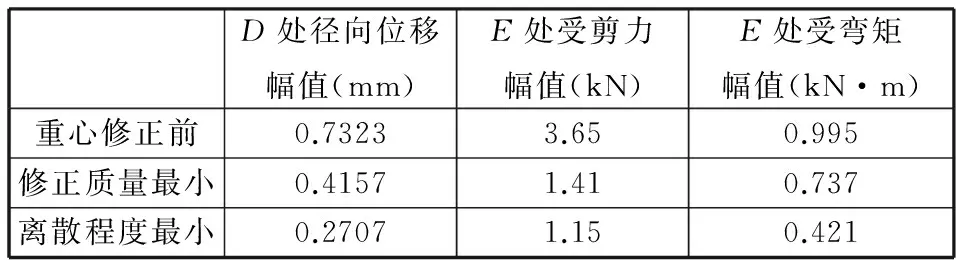
表2　重心修正前后仿真結果

5　結論

(1)針對船槳槳葉重心誤差評價問題,提出重心的最小包容球和重心公差球的概念，并給出具體算法，為槳葉重心評價提供可靠的理論依據。

(2)根據重心組合原理，給出了修正區域的確定方法，并分別以最小修正質量和最小槳葉重心離散程度為標準提出最優修正方案。

(3)對修正前后螺旋槳主軸的力學性能進行分析，仿真結果與理論分析結果相符。

(4)結果表明螺旋槳在重心評價和兩種重心修正方案優化后，力學性能較修正前有不同程度的改善，有效地減小了重心偏差對螺旋槳的影響，其中修正質量最小方案修正后的槳葉表面形狀改變較小，進而對螺旋槳水動力性能影響較小；以最小離散程度方案修正后的螺旋槳的力學性能改善效果更明顯。所提出的重心評價和修正方法也為類似的多槳葉組合槳的重心改善問題提供可靠的參考依據。

[1]梁延德,郭超,王治雄,等.大型復雜曲面工件重心傾側方法研究[J].組合機床與自動化加工技術,2013(12):1-3.

Liang Yande,Guo Chao,Wang Zhixiong,et al.Study on the Tilt Measurement of the Gravity Center for Large Workpiece with Complex Surface[J].Modular Machine Tool and Automatic Manufacturing Technique,2013(12):1-3.

[2]戈賁奇,朱新河.船用銅合金螺旋槳的檢驗要點分析[J].大連海事大學學報,2005,31(2):55-58.

Ge Benqi,Zhu Xinhe.Examination Important Point Analysis of the Marine Propeller Made of Copper Alloy[J].Journal of Dalian Maritime University,2005,31(2):55-58.

[3]謝偉.五葉調距槳的槳葉優化組合及整槳靜平衡方法研究[J].艦船科學技術,2004,26(5):7-10.

Xie Wei.Study on Optimum Combination of Blades of Five-blade Controllable-pitch Propeller and Static Balancing Methods of the Whole Propeller[J].Ship Science and Technology,2004,26(5):7-10.

[4]于穎,於孝春,關琦.螺旋槳槳葉葉面加工過程中加工量的計算[J].機械設計與制造,2003(5):100-101.

Yu Ying,Yu Xiaochun,Guan Qi.Calculation of Manufacturing Value of the Curve Surface of Blades of the Propeller[J].Machinery Design and Manufacture,2003,5:100-101.

[5]李芳.槳葉重心檢測系統設計[C]//中國智能交通年會優秀論文集.北京:中國智能交通協會,2009:90-92.

[6]顧毅君,徐冰強,陸金桂,等.粒子群優化算法在螺旋槳加工量計算中的應用[J].現代制造工程,2009,8(1):6-8.

Gu Yijun,Xu Bingqiang,Lu Jingui,et al.The Application of PSO Algorithm on Computing Manufacturing Allowance of Propeller[J].Modern Manufacturing Engineering,2009,8(1):6-8.

[7]曾艷,李斌,彭芳瑜,等.面向數控加工的大型螺旋槳槳葉的余量估算問題研究[J].中國機械工程,2006,17(3):566-569.

Zeng Yan,Li Bin,Peng Fangyu,et al.Research on the Estimation of the Propeller Allowance in NC Machining[J].China Mechanical Engineering,2006,17(3):566-569.

[8]Yildirim E A.Two Algorithms for the Minimum Enclosing Ball Problem[J].SIAM Journal on Optimization,2009,19(3):1368-1391.

[9]Pan Shaohua,Li Xingsi.An Efficient Algorithm for the Smallest Enclosing Ball Problem in High Dimensions[J].Applied Mathematics and Computation,2006,172(1):49-61.

[10]金鑫,何玉林,劉樺,等.風力發電機耦合振動分析[J].振動與沖擊,2007,26(8):144-147.

Jin Xin,He Yulin,Liu Hua,et al.Coupled Vibration Analysis of Wind Turbine[J].Journal of Vibration and Shock,2007,26(8):144-147.

(編輯袁興玲)

Barycenter Error Evaluation and Correction for Modular Marine Propeller

Liang YandeSun JiefuHe FubenLu Yaheng

Dalian University of Technology,Dalian,116024

In the process of blade manufacturing,there existed the influences of manufacturing precision,material defects,assembling errors and other non-design factors,which caused the difference between actual position and theoretical position of modular marine propeller barycenters.There would have adverse effects on its mechanical properties.Hence,it was necessary to evaluate the barycenters and remove the weights so as to correct the barycenter position errors of relevant blades.The concepts and the algorithms of minimum containing ball and removal processing ball were proposed,which could be applied to determine whether the blade needed to be re-processed.Meanwhile,regarding the barycenter combination,two weight correction solutions were also proposed based on the principles of the minimum amount of correction weight and the minimum dispersion degree of barycenter respectively.In the end,the feasibility of strategy was evaluated by applying theoretical analysis and simulation experiments.

modular marine propeller;minimum containing ball;removal processing ball;minimum correction weight;degree of barycenter dispersion

2014-04-02

TH161DOI：10.3969/j.issn.1004-132X.2015.06.009

梁延德,男,1953年生。大連理工大學機械工程學院教授。研究方向為先進制造技術,精密加工。孫捷夫,男,1991年生。大連理工大學機械工程學院碩士研究生。何福本,男,1984年生。大連理工大學機械工程學院博士研究生。魯亞恒,男,1991年生。大連理工大學機械工程學院碩士研究生。