通用量子門神經網絡在齒輪故障診斷中的應用

李　勝　張培林　李　兵　王國德

1.軍械工程學院,石家莊,050003　　2.武漢軍械士官學校,武漢,430075

通用量子門神經網絡在齒輪故障診斷中的應用

李勝1張培林1李兵1王國德2

1.軍械工程學院,石家莊,0500032.武漢軍械士官學校,武漢,430075

為進一步提高齒輪故障診斷能力,結合目前神經網絡機理的研究進展,建立了一種基于通用量子門的量子神經元模型,提出了通用量子門神經網絡(universal quantum gate neural network,UQGN)算法。首先,該算法將轉換后的量子態訓練樣本作為輸入。然后,利用量子旋轉門和通用量子門完成旋轉、選擇、翻轉和聚合等一系列操作，并完成網絡參數的更新。最后，將訓練后的結果輸出。在數學上，證明了UQGN算法的泛化能力。利用該算法對齒輪的正常、齒面磨損、齒根裂紋和斷齒4種情況進行了模式識別。實驗結果表明，與普通神經網絡和普通量子神經網絡相比，UQGN算法在泛化性能、魯棒性、準確率和執行時間等方面具有較好的效果。

量子計算;通用量子門;量子神經網絡;齒輪;故障診斷

0　引言

目前,應用于齒輪故障診斷中的模式識別方法主要有小波變換、神經網絡、支持向量機等。量子計算具有量子干涉和量子糾纏等特性,與經典計算相比,它可以極大地提高運算速度和縮小存儲空間[1]。由于量子神經網絡(quantum neural network,QNN)具有提高神經網絡的逼近能力和信息處理效率的優點,被廣泛應用在模式識別、函數逼近、優化PID控制參數等方面[2-4]。在齒輪故障診斷方面,文獻[5-6]對齒輪箱故障信號進行量子特征提取,并采用量子神經網絡進行故障診斷,取得了不錯的效果。

目前,量子神經網絡的研究主要體現為以傳統神經網絡的結構,引入量子理論的概念,建立量子神經網絡模型。根據文獻[7]的研究結果,本文提出了一種基于通用量子門的量子神經網絡學習算法。該算法建立了一種新的量子神經元模型,并采用Levenberg-Marquardt(LM)法確定了旋轉角度的大小和方向。運用本文方法對齒輪的正常、齒面磨損、齒根裂紋和斷齒的故障信號進行了模式識別,實驗結果表明,與普通神經網絡CNN和普通量子神經網絡CQN相比,通用量子門神經網絡(universal quantum gate neural network,UQGN)在泛化性能、魯棒性、準確率和執行時間等方面具有明顯的優勢。

1　通用量子門神經網絡

1.1通用量子門神經元模型

U=Φ(δ)Rz(α)Ry(θ)Rz(β)

(1)

其中,α、β、δ、θ為實參數。

本文的通用門量子門神經元主要由輸入、旋轉、選擇、翻轉、聚合、輸出等操作組成。圖1為通用量子門神經元模型。

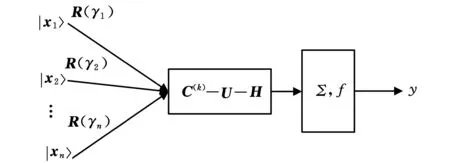
圖1　通用量子門神經元模型

圖1中,輸入為量子位|X〉=[|x1〉|x2〉…|xn〉],R(γn)用于量子相位的旋轉操作,通用量子門C(k)-U-H用于選擇和翻轉操作,C(k)為第k次的受控非門，H為Hadamard門,Σ為求和算子,f為目標函數，y為量子位處于|1〉的概率幅輸出。

設|xi〉=[cosφisinφi]T,則

R(γi)|xi〉=[cos(φi+γi)sin(φi+γi)]T

(2)

HUCR(γi)|xi〉=

(3)

在圖1中,通用量子門神經元的輸入輸出關系為

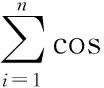
(4)

1.2通用量子門神經網絡模型

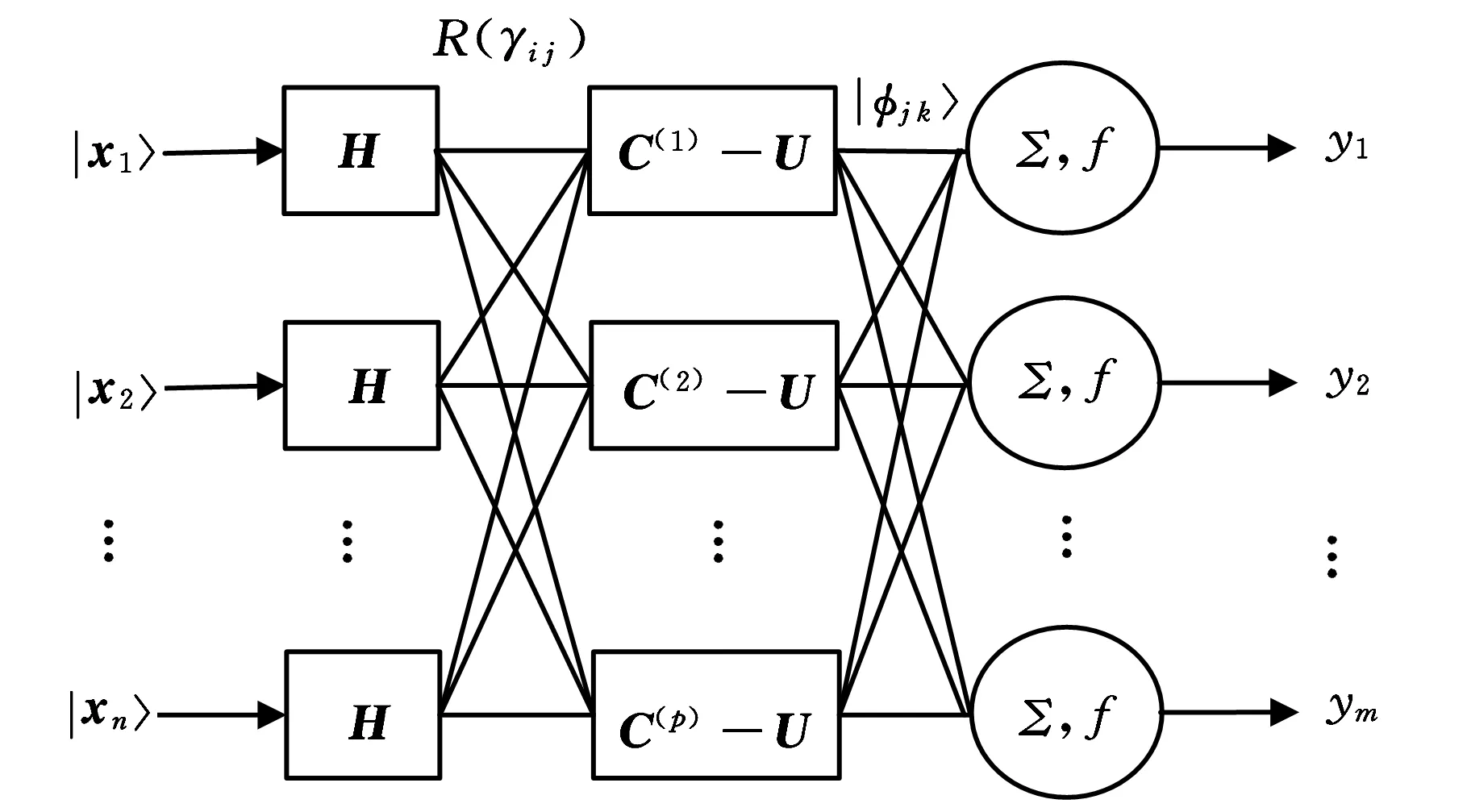
圖2　三層通用量子門神經網絡模型

本文提出的通用量子門神經網絡是按照一定的拓撲結構將若干個通用量子門神經元連接組合而成的。本文采用三層神經網絡,即輸入層、隱含層和輸出層，圖2描述了本文的神經網絡模型。其中,輸入層、隱含層和輸出層分別有n、p和m個神經元。圖2中各參數代表的意義為:|xi〉為網絡輸入,ym為網絡輸出,R(γi j)為輸入層和隱含層之間的連接權值,|φj k〉為隱含層和輸出層之間的連接權值。H和C(p)-U分別為輸入層和隱含層的傳遞函數。通用量子門神經網絡模型的輸入輸出關系為

hj=UCR(γi j)H|xi〉=

(5)

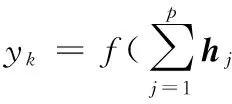
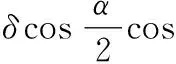
(6)

i=1,2,…,n;k=1,2,…,m

1.3樣本的量子態描述

已知在沒有湍流的情況下，距離出射平面L處的場強可以通過Huygens-Fresnel積分得到輸出場強表達式.在真空中傳輸L距離后的場強UL(r,θ,L) 表示為[15]

由于訓練樣本集初始狀態為實數值，應相應地轉換為神經網絡模型的量子態輸入,即X=[x1x2…xn]T?|X〉=[|x1〉|x2〉…|xn〉]T轉換公式為

|xi〉=cosφi|0〉+sinφi|1〉=[cosφisinφi]T

(7)

1.4模型參數的更新規則

在通用量子門神經網絡模型中,共有6組參數,其中,α、β、δ、θ為給定實數值。參數γi j和φj k采用LM法進行更新。

定義神經網絡的性能指數為

(8)

根據LM方法,γi j和φj k的更新公式為

Δγi j=(JT(γi j)J(γi j)+λ1I)-1JT(γi j)e(γi j)

(9)

Δφj k=(JT(φj k)J(φj k)+λ2I)-1JT(φj k)e(φj k)

(10)

其中,λ1和λ2為0.01;J(γi j)和J(φj k)為雅可比矩陣：

(11)

(12)

與普通量子門神經網絡相比,通用量子門神經網絡主要有以下優勢：①采用通用量子門可以進行任意的幺正變換，能將運算速度提高，便于實施程序編譯。②采用LM方法而不是梯度下降法進行參數更新，可以提高參數的收斂速度，防止陷入局部極小點。③神經網絡模型中的連接權值全部采用量子態描述，達到運算的一致性。

2　通用量子門神經網絡泛化性能分析

在量子計算過程中,一系列量子門的操作會造成一些誤差。假設誤差是幺正的,設為on。幺正誤差越小,所導致的泛化誤差越小,從而神經網絡的性能也就越好。在通用量子門神經網絡模型中,幺正誤差on為

(13)

定理若x∈Cn,y∈Cm,對?ε>0,?σ>0,當|on|<σ,則E<ε。

證明對?σ>0有：

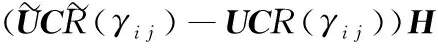
則神經網絡模型的泛化誤差為

設mσ2/2=ε,由于ε>0,σ>0,因此,E

3　齒輪故障診斷及結果分析

采用本文算法進行模式識別,進一步驗證模型的有效性和泛化性，并與普通神經網絡和普通量子神經網絡進行對比分析。

3.1齒輪故障信號的采集和特征提取

齒輪的故障振動信號采集于一個二級傳動齒輪箱，傳感器型號為CA-YD-185,將傳感器安裝在齒輪箱的軸承座上。對齒輪的正常、齒面磨損、齒根裂紋和斷齒等4種狀態進行信號采集。設定齒輪轉速為600r/min,采樣點數為2048,采樣頻率為12 800Hz。齒輪的時域波形圖見圖3。對每一種狀態共采集50個樣本，其中，選取15個作為訓練樣本，其余35個作為測試樣本。

圖3　齒輪4種狀態下的時域波形圖

由圖3可以看出,在時域上,4種工作狀態的振動信號之間有很明顯的差異。齒面磨損時，噪聲稍有加強;齒根裂紋時,在裂紋處有較強的信號;斷齒時,噪聲明顯,且斷齒處的振動信號變強。

齒輪的故障特征集是由時域信號的10個統計參數組成的，這10個統計參數分別為峰峰值、均方值、方差、方根幅值、均方幅值、峭度、波形指標、峰值指標、脈沖指標、邊界指標。因此,共得到40個特征參數。同時，對提取出的特征參數集進行歸一化處理，以降低特征參數間的差異性。歸一化公式為

(14)

3.2齒輪故障信號的模式識別

為了便于比較普通神經網絡、普通量子神經網絡和通用量子門神經網絡的性能，將三個神經網絡的結構統一設定為10-25-4,迭代步數t為1000，限定誤差為0.05。其中，通用量子門神經網絡的參數設置如下：γi j和φj k的初始值為0.01π,α=θ=0.25π,β=0.1π,δ=0.125π。普通神經網絡和普通量子神經網絡的參數設置如下：學習速率為0.9。

(1)迭代步數與泛化誤差。圖4所示為三種算法迭代步數與泛化誤差的關系。由圖4可見，當迭代步數不斷增加時，這三種神經網絡模型的泛化誤差會不斷地減小。其中，UQGN在迭代步數為447時，泛化誤差達到0.049并保持穩定;CQN在迭代步數為686時,泛化誤差達到0.051并保持穩定;CNN在迭代步數為810時,泛化誤差達到0.084并保持穩定。這樣可以說明,UQGN算法的迭代步數遠遠小于CQN和CNN的迭代步數，并且算法的泛化誤差更小,因此,UQGN具有很好的泛化性和魯棒性。

圖4　迭代步數與泛化誤差的關系

圖5　迭代步數與分類準確率的關系

(2)迭代步數與分類準確率。圖5所示為三種算法迭代步數與分類準確率關系的對比結果。由圖5可以看出,隨著迭代步數的增加,分類準確率也跟著提高。UQGN算法在迭代步數為570時,分類準確率達到98.5%;CQN算法在迭代步數為750時，分類準確率達到95.4%;CNN算法在迭代步數為860時,分類準確率達到91.2%。通過對比發現,相比于CNN和CQN算法,UQGN算法的收斂性更好,收斂速度快,并且分類準確率較高。

(3)準確率統計和執行時間。利用UQGN、CQN和CNN算法分別進行20次獨立訓練。表1所示為算法的結果。由表1可以看出,UQGN的最大準確率達到了99.1%,比CQN和CNN算法的準確率要高,同時,UQGN算法的執行時間也縮短了很多。因此,UQGN算法具有較高的分類準確率和較短的執行時間。

表1　三種算法的結果

綜上所述,通用量子門神經網絡在泛化性能、魯棒性、準確率和執行時間上具有明顯好于普通神經網絡和普通量子神經網絡的優勢。

[1]李士勇，李盼池. 量子計算與量子優化算法[M]. 哈爾濱：哈爾濱工業大學出版社，2009.

[2]李飛,趙生妹,鄭寶玉.量子神經網絡及其在CDMA多用戶檢測中的應用[J].信號處理,2005,21(6):555-559.

Li Fei,Zhao Shengmei,Zheng Baoyu.Quantum Neural Networks and Its Application in CDMA Multiuser Detection[J].Signal Processing,2005,21(6):555-559.

[3]熊和金，桂啟發. 量子神經網絡動力學及其在信息安全中的應用[J].浙江萬里學院學報,2003,16(2):10-13.

Xiong Jinhe,Gui Qifa.Dynamics of Quantum Neural Networks and Its Applications to Information Security[J].Journal of Zhejiang Wanli University,2003,16(2):10-13.

[4]于瓅,汪家權.改進的QGA-BP模型在復雜水質預測中的應用[J].模式識別與人工智能,2012,25(4):705-708.

Yu Li,Wang Jiaquan.Application Research on Complex Water Quality Prediction with Improved QGA-BP Model[J].Pattern Recognition and Artificial Intelligence,2012,25(4):705-708.

[5]崔曉靜.基于量子特征與ICA技術的齒輪箱故障診斷研究[D].沈陽:中北大學,2011.

[6]李悅.量子ICA技術在故障診斷中的應用研究[D].沈陽:中北大學,2012.

[7]Quiroga R Q,Fired I,Koch C.Brain Cells for Grandmother[J].Scientific American,2013,308(2):30-35.

[8]Benenti G,Casati G,Strini G.Principle of Quantum Computation and Information I[M].Singapore:World Scientific,2007.

(編輯袁興玲)

Application of Universal Quantum Gate Neural Network in Gear Fault Diagnosis

Li Sheng1Zhang Peilin1Li Bing1Wang Guode2

1.Ordnance Engineering College,Shijiazhuang,050003 2.Wuhan Ordnance Non-Commissioned Officer Academy,Wuhan,430075

In order to improve the ability of gear fault diagnosis,considering the current research of neural network mechanism,a quantum neuron model was proposed based on universal quantum gate and an universal quantum gate neural network(UQGN) was established.Firstly,the input was quantum training samples after transformed.Then,quantum rotation gate and an universal quantum gate were used for rotation selection overturn and aggregation,and the network parameters were updated.Finally,the trained results were as output.The generalization performance of UQGN was proved in mathematics.The proposed method was applied to pattern recognition of gear fault conditions.The experimental results indicate that, compared with common neural network and common quantum neural network,UQGN has better effects on generalization performance, robustness accuracy and execution time.

quantum computation;universal quantum gate;quantum neural network;gear;fault diagnosis

2014-02-04

國家自然科學基金資助項目(E51205405)

TP18DOI：10.3969/j.issn.1004-132X.2015.06.012

李勝, 男, 1986年生。 軍械工程學院七系車輛工程教研室博士研究生。主要研究方向為量子優化與智能識別算法，已發表12篇論文。張培林，男，1955年生。軍械工程學院七系車輛工程教研室教授、博士研究生導師。李兵，男，1982年生。軍械工程學院四系中程導彈教研室博士、副教授。王國德，男，1986年生。武漢軍械士官學校高炮教研室講師。