基于連續蟻群算法的3-RPS并聯機構正解
謝志江 梁 歡 宋代平
重慶大學機械傳動國家重點實驗室,重慶,400030
基于連續蟻群算法的3-RPS并聯機構正解
謝志江梁歡宋代平
重慶大學機械傳動國家重點實驗室,重慶,400030
為了避免傳統數值方法求解并聯機構正解問題的弊端,提出了一種將并聯機構正解問題轉化為目標函數優化問題的求解方法。并聯機構正解的核心問題是求解一組多元耦合非線性方程組,以此為依據建立了并聯機構正解的目標函數優化模型,并提出了一種簡單的連續蟻群算法來求解該優化模型。以求解3-RPS并聯機構正解為例進行了仿真分析。結果表明,該算法具有良好的全局尋優功能,能夠避免初始值和局部極小值對計算結果的影響,不用計算雅可比矩陣及其逆陣,且計算精度滿足并聯機構正解的要求。
并聯機構;運動學正解;蟻群算法;多目標優化
0 引言
并聯機構坐標測量機以其測量誤差小、測頭位置靈活、成本較低等優點,成為坐標測量機領域研究的新熱點[1]。該測量機測量模型的原理從本質上來說是并聯機構位置正解,因此一種高效、精確的并聯機構正解算法對提高并聯機構坐標測量機測量精度是非常重要的。
并聯機構位置正解的核心問題一般歸結為求解一組多元耦合的非線性方程組。傳統算法分解析法和數值法[2]兩種。解析法主要是通過消元法得到單獨參數多項式,然后再求解。這種方法不需要設置初始值,并且能夠求得全部解,避免位置奇異問題。程世利等[3]提出了一種6-SPS并聯機構運動學正解的解析方法。但是,該方法推導過程復雜,不具有通用性,一種解析方法僅求解一種模型。數值法主要是通過Newton法或Newton-Raphson法迭代求解[4-5],該方法需要設置初始值并且每次迭代都需要計算雅可比矩陣及其逆陣,因此該類方法計算速度較慢且計算精度受初始值的影響較大。韓方元等[6]提出了一種3-RPS并聯機構正解的快速數值算法,該算法迭代過程中不需要計算雅可比矩陣及其逆陣,但對機構的結構具有一定的依賴性,通用性較差。
本文先將非線性方程組轉化成多目標優化問題,再根據權和法將多目標優化轉化成單目標優化,最后采用連續蟻群算法進行求解。
1 并聯機構逆解分析
圖1為三坐標測量機3-RPS并聯機構的機構簡圖,該機構由底部定平臺、頂部動平臺以及三條支鏈構成,各支鏈在平臺上均勻分布且從下向上依次為轉動副(R)、移動副(P)、球副(S)。通過驅動移動副,改變三條支鏈的長度來實現動平臺的運動,該并聯機構具有三個自由度,即繞x軸、y軸的轉動以及沿z軸的移動。
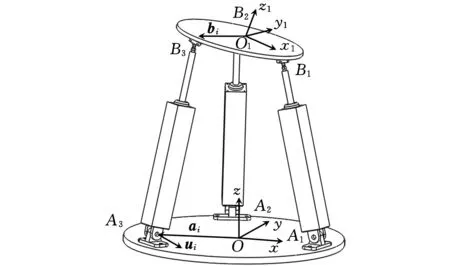
圖1 3-RPS并聯機構簡圖
如圖1所示,在底部定平臺幾何中心建立定坐標系Oxyz,x軸過A1點,y軸與A3A2平行,z軸方向垂直定平臺向上。在頂部動平臺幾何中心建立動坐標系O1x1y1z1,x1軸過B1點,y1軸與B3B2平行,z1軸方向垂直動平臺向上。上下平臺半徑分別為rb和Ra,ai表示Ai點在定坐標系Oxyz的矢量,bi表示Bi點在動坐標系O1x1y1z1的矢量,p表示O1點在定坐標系Oxyz的矢量,坐標為(x,y,z),li表示第i條支鏈的長度,ni表示各支鏈方向的單位向量。則有
ai=Ra(cosθi,sinθi,0)T
bi=rb(cosθi,sinθi,0)T
由圖2封閉矢量圖可得
lini=Rbi+p-ai
(1)
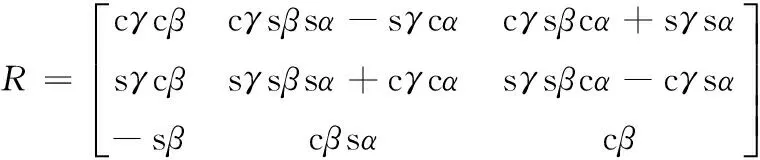
其中,R表示動坐標系O1x1y1z1相對于定坐標系Oxyz的旋轉變換矩陣,α、β、γ分別為Z-Y-X型的歐拉角,c代表cos,s代表sin。
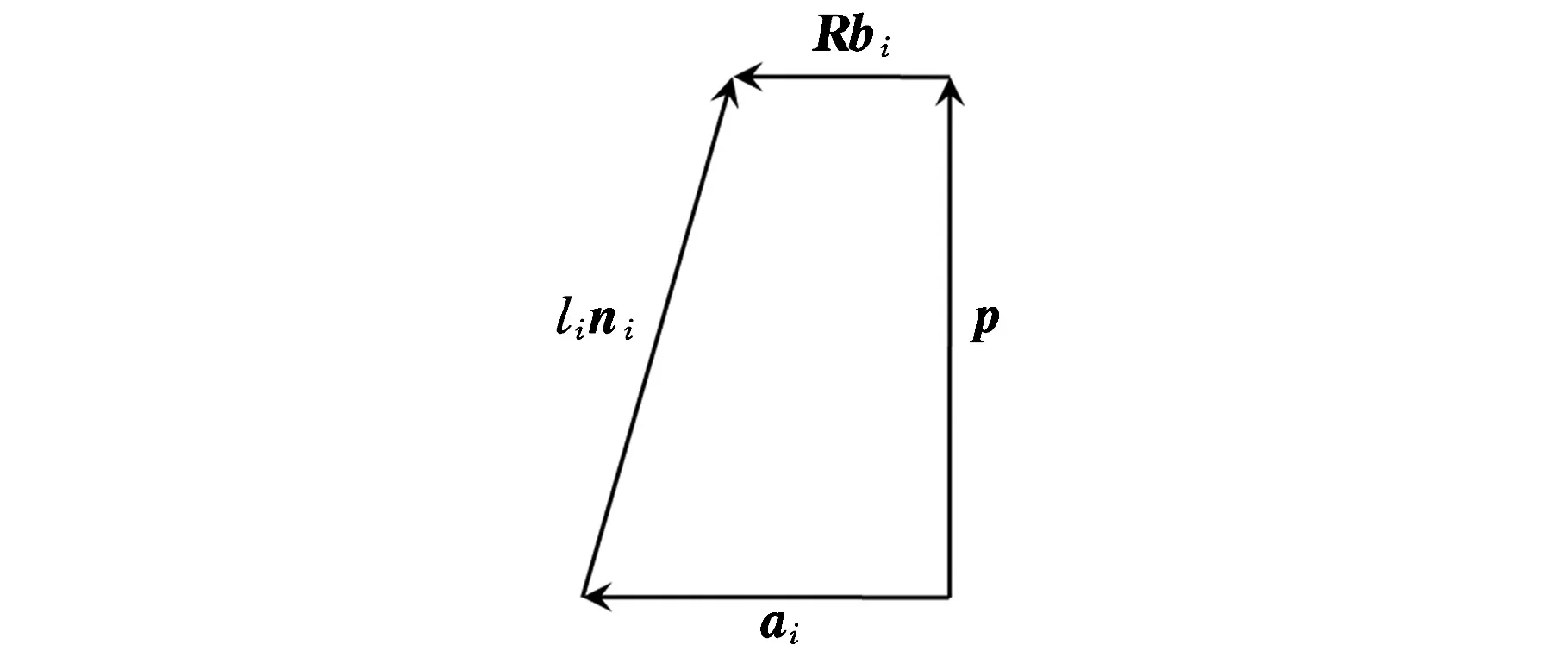
圖2 封閉矢量圖
各條支鏈受轉動副的約束,只能在三個垂直平面內運動,可得
Rbi·ui=0
(2)
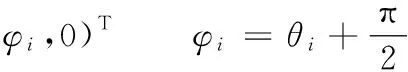
式中,ui為各轉動副軸線方向的單位向量。
由式(2)可得
(3)
將式(3)代入式(1)可得各支鏈長li為
(4)
則機構的逆解可以記為
li=fi(α,β,z)
(5)
2 機構正解的目標優化模型
機構正解的本質是求解一組非線性方程組,由式(4)可得該方程組:
i=1,2,3
(6)
將該非線性方程組轉化成多目標優化問題,即求解式(7)的最小值:
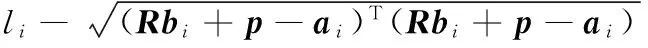
(7)
權和法可以將多目標優化問題轉化為所有目標的加權和的標量問題,即:
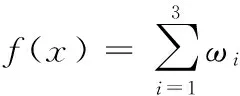
(8)
式中,ωi為權重系數。
將式(7)代入到式(8)中,可得機構正解數學優化模型:
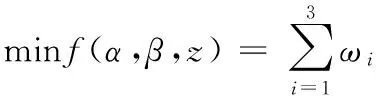
(9)
由于要求式(6)為零,所有各子目標函數權重系數相等,為計算簡便,故取ωi=1。
3 連續蟻群算法
蟻群算法是一個求解離散問題的數學模型[7]。而目標函數的優化是一個連續域的優化問題,因此需要一種適用于連續域內的蟻群算法。一種簡單的方式是在目標函數可行域打網格,將連續空間離散化,再使用蟻群算法進行求解[8],該方法存在求解精度不高,搜索空間大等缺點。Dero等[9]提出了一種適用于連續域內的蟻群算法,該方法采用信息素的傳遞以及直接交流兩種方式結合來指導蟻群的尋優;文獻[10-12]也提出了幾種適用于連續域內的蟻群算法。在前人的基礎上,本文提出一種較為簡單的連續蟻群算法。
該連續蟻群算法的基本思路如下:
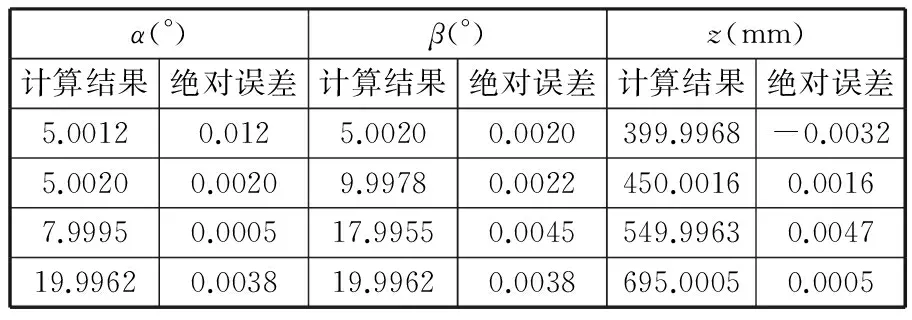
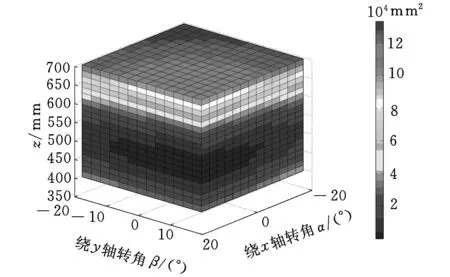
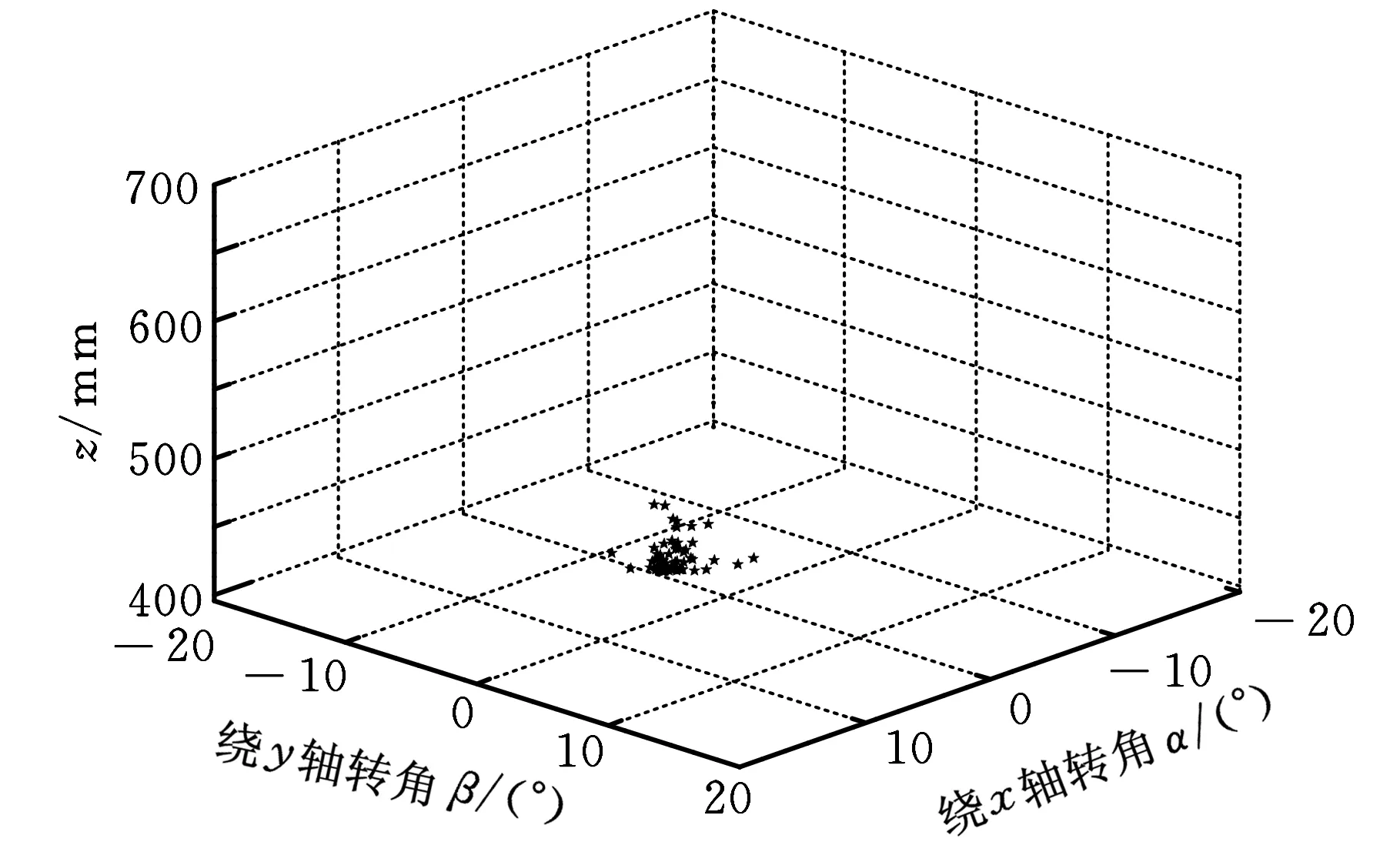
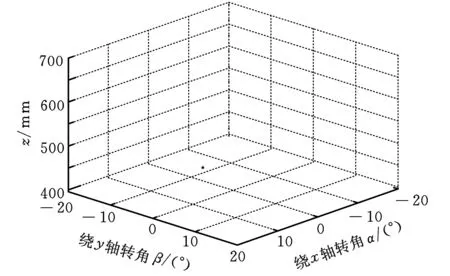
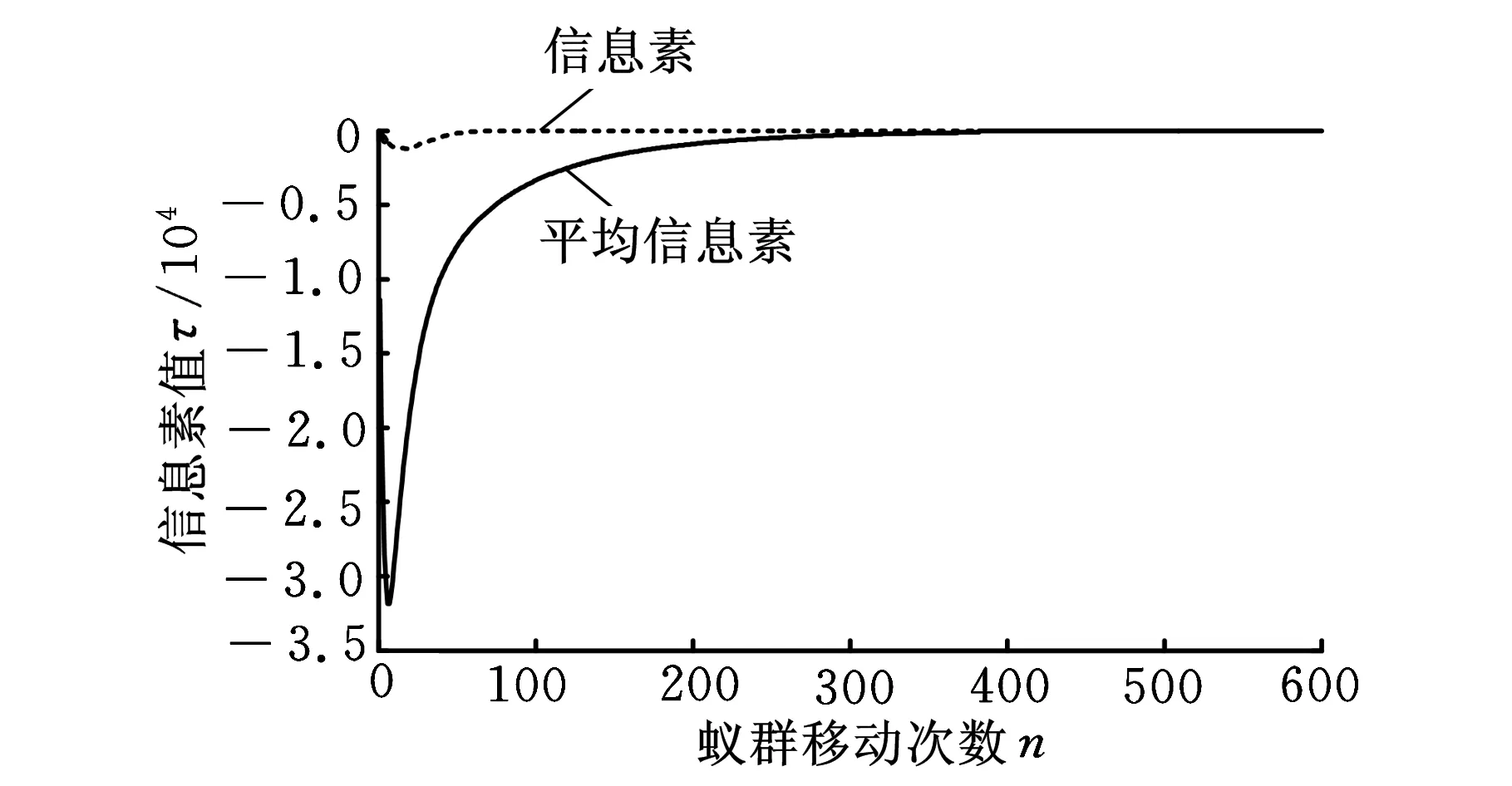
首先根據三坐標測量機3-RPS并聯機構的空間運動范圍設定機構各自由度取值范圍:αl<α<αu,βl<β<βu,zl (1)在各變量的可行域αl<α<αu,βl<β<βu,zl (2)根據目標函數確定信息素的大小,信息素的表達式為 τ=-f(α,β,z) (10) 其增減性與目標函數相反,本文求目標函數最小值,即信息素的最大值。因為f(α,β,z)正向無限趨近0時,其信息素值負向無限趨近于0,從而不便于衡量信息素的濃度,故同時也用式(11)平均信息素值進行衡量: τmean=mean(-f(α,β,z)) (11) 式中,mean()為取平均值函數。 (3)由式(10)確定蟻群初始位置時信息素值的大小,從中記錄最優值τbest并計算平均信息素值τmean的大小。 (4)蟻群轉移概率決定了蟻群進行全局搜索還是局部搜索,表達式為 (12) 其中,i表示第i次蟻群移動,j表示第j只螞蟻,τi,j表示第i次蟻群移動后第j只螞蟻所對應的信息素值。 (6)蟻群移動完成一次,對每只螞蟻的信息素值進行更新,如下式所示: (13) 式中,ρ為信息素殘留系數。 (7)如此反復迭代,當迭代次數n小于規定最大循環次數,轉至步驟(4),否則跳出循環,輸出最終解。 圖1所示3-RPS并聯機構的參數如下:定平臺半徑Ra=257 mm,動平臺半徑rb=141 mm,機構各自由度運動范圍為:α,β∈[-20°,20°],z∈[395,695]mm。 本文以求解當α= 15°,β=10°,z=495 mm位置時的正解為例,驗證連續蟻群算法在求解并聯機構正解的有效性。其他位置求解結果如表1所示。而采用傳統Newton-Raphson法對該位置求解,結果如表2所示。 表1 連續蟻群算法計算結果 表2 Newton-Raphson法計算結果 由3-RPS逆解求得三條支鏈長度分別為:l1=485.3 mm,l2=553.5 mm,l3=490.3 mm。可得目標函f(α,β,z)在空間可行域內的值域,如圖3所示。 圖3 目標函數f(α,β,z)的值域 正解問題可以轉化為尋找該立方體中的最小值,將蟻群隨機分布在如圖3所示區域中,為了觀察方便,將立方體圖剖開,并將顏色淡化,如圖4所示。 圖4 螞蟻初始位置分布圖 采用連續蟻群算法進行計算,所有螞蟻聚集在目標函數f(α,β,z)的最小值處,不受局部最小值的影響,如圖5、圖6所示。 圖5 螞蟻運動300次位置分布圖 圖6 螞蟻運動600次位置分布圖 該算法的收斂速度可從信息素以及平均信息素值的變化看出,如圖7所示。 圖7 最大信息素值和平均信息素值 由以上計算可得,當目標函數f(α,β,z)取最小值時,α=15.0020°,β=10.0016°,z=495.0071 mm,f(α,β,z)=-2.25×10-4,計算精度滿足要求。 從以上仿真分析中可以看出,采用Newton-Raphson法計算的結果直接受初始值的影響,不同的初始值計算結果偏差很大;而采用本文提出的連續蟻群算法,可以避免初始值對計算結果的影響,得到精確解。 本文通過將求解并聯機構正解的非線性方程組轉化成目標函數的最優化問題,采用連續蟻群算法進行求解,避免了初始值的選取對計算精度的影響。不需要求解雅可比矩陣及其逆陣,計算過程簡便快捷。采用全局搜索和局部搜索相結合的方法,計算結果不受局部極小值的影響。該方法適用于求解所有并聯機構正解問題,具有良好的通用性。 [1]胡鵬浩,李松原.3-PSS并聯機構正解及其在坐標測量機中的應用[J].光學精密工程,2012,20(4):782-788. Hu Penghao,Li Songyuan.Kinematic Solution of 3-PSS Parallel Mechanism and Its Application in Parallel CMM[J].Optics and Precision Engineering,2012,20(4):782-788. [2]季曄,劉宏昭,原大寧.并聯機構位置正解方法研究[J].西安理工大學學報,2010,26(3):277-281. Ji Ye,Liu Hongzhao,Yuan Daning Research on Approach of Forward Positional Analysis of Parallel Mechanism[J].Xi’an University of Technology Newspaper,2010,26(3):277-281. [3]程世利,吳洪濤,姚裕.6-SPS并聯機構運動學正解的一種解析化方法[J]. 機械工程學報,2010,46(9):26-31. Cheng Shili,Wu Hongtao,Yao Yu.An Analytical Method for the Forward Kinematics Analysis of 6-SPS Parallel Mechanisms[J].Chinese Journal of Mechanical Engineering,2010,46(9):26-31. [4]Lee K,Shah K D.Kinematic Analysis of a Three Degrees of Freedom in-parallel Actuated Manipulator[J].IEEE Journal of Robotics and Automation,1988,4(3):361-367. [5]Hashimoto M,Imamura Y.Kinematic Analysis and Design of a 3 DOF Parallel Mechanism for a Passive Compliant Wrist of Manipulators[J].Transactions of the Japan Society of Mechanical Engineers,1998,64:2116-2123. [6]韓方元,趙丁選,李天宇.3-RPS并聯機構正解快速數值算法[J].農業機械學報,2011,42(4):229-233. Han Fangyuan,Zhao Dingxuan,Li Tianyu.A Fast Forward Algorithm for 3- RPS Parallel Mechanism[J].Transactions of the Chinese Society of Agricultural Machinery,2011,42(4):229-233. [7]申鉉京,劉陽陽,黃永平.求解TSP問題的快速蟻群算法[J].吉林大學學報,2013,43(1):147-151. She Xuanjing,Liu Yangyang,Huang Yongping.Fast Ant Colony Algorithm for Solving Traveling Salesman Problem.Journal of Jilin University,2013,43(1):147-151. [8]高尚,楊靜宇.群智能算法及其應用[M].北京:中國水利水電出版社,2006. [9]Dero J,Siam P.Continuous Interacting Ant Colony Algorithm Based on Dense Heterarchy[J].Future Generation Computer Systems,2004,5(20):841-856.[10]Li Y J,Wu T J.An Adaptive Ant Colony System Algorithm for Continuous Space Optimization Problems[J].Journal of Zhejiang University:Science,2003,4(1):40-46. [11]Karaboga N,Kalinli A,Karaboga D.Designing Digital IIR Filters Using Ant Colony Optimization Algorithm[J].Engineering Application of Artificial Intelligence,2004,17(2):301-309. [12]Socha K,Dorigo M.Antcolony Optimization for Continuous Domains[J].European Journal of Operational Research,2008,185(3):1155-1173. (編輯袁興玲) Forward Kinematics of 3-RPS Parallel Mechanism Based on a Continuous Ant Colony Algorithm Xie ZhijiangLiang HuanSong Daiping The State Key Laboratory of Mechanical Transmission,Chongqing University,Chongqing,400030 In order to avoid the drawbacks of traditional numerical methods for solving the problem of parallel mechanism forward kinematics,this paper proposed a method that translated the problem of solving parallel mechanism forward kinematics into objective function optimization problems. The central issue of solving the problem of parallel mechanism forward kinematics was to solve a set of multiple coupled nonlinear equations,thus objective function optimization model of parallel mechanism forward kinematics was established,and a kind of simple continuous ant colony algorithm was put forward to solve the above optimization model.Taking the 3-RPS parallel mechanism for example,some simulation analyses were completed.The results show that the algorithm has a good global optimization function and can avoid initial values and the local minimum effect on the calculation results without calculating Jacobian matrix and its inverse matrix.The accuracy of calculation meets the requirements of parallel mechanism of forward kinematics. parallel mechanism;forward kinematics;ant colony algorithm;multi-objective optimization 2014-03-10 國家自然科學基金資助項目(51105392);重慶市自然科學基金資助項目(cstc2011jjA70006);中央高校基本科研業務費專項資金資助項目(CDJRC10110005) TP391.9;TH112DOI:10.3969/j.issn.1004-132X.2015.06.017 謝志江,男,1963年生。重慶大學機械傳動國家重點實驗室教授、博士研究生導師。主要研究方向為機械創新設計。梁歡,男,1988年生。重慶大學機械傳動國家重點實驗室碩士研究生。宋代平,男,1979年生。重慶大學機械工程學院副教授。
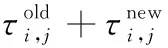
4 求解機構正解實例

5 結束語

