鋰電池極片輥壓機剛度分析與結構優化

馬嵩華　田　凌

1.山東大學,濟南,250013　　2.清華大學,北京,100084

鋰電池極片輥壓機剛度分析與結構優化

馬嵩華1田凌2

1.山東大學,濟南,2500132.清華大學,北京,100084

在鋰電池極片加工過程中，由于其高能量密度要求與涂覆材料力學性能存在矛盾，故需要根據極片所需壓縮比嚴格控制輥壓力的大小，而實際中,軋輥特性使兩輥之間窄縫距離的直接測定不容易,因此難以通過物理樣機試驗的方式直接得到生產過程中輥縫與輥壓力之間的關系。針對該問題，簡化了輥壓過程中的物理量,建立了整機和極片變形的數學模型，利用數學模型間接得到整機輥壓力與輥縫變化之間的定量關系。采用仿真驅動設計的方式，基于響應面法和多目標優化算法得到整機的設計優化結果。測試試驗表明,簡化的數學模型可以數字化地描述輥壓機的工作情況，便于指導生產中控制極片的制造工藝參數，同時基于響應面的設計優化提高了輥壓機的設計生產效率。

輥壓機；鋰電池極片；有限元分析；優化設計

0　引言

人們對移動設備日益增長的需求對電池提出了高能量密度、長循環壽命、高電壓、安全、低廉等要求。為提高電池儲能能力，保證極片材料的壓實程度，需要對極片進行輥壓。極片輥壓機作用的對象為厚0.2 mm左右的電池極片,表面精度幾微米,以鋁箔和銅箔為基體,上面涂覆活性物質，表現出復雜的彈塑性變形，軋制過程要求壓力可以從1.03 MN(103 t)到0.6 MN(60 t)變化。目前,鋰電池廠家采用試錯法確定軋制工藝參數,該方法工作效率低,且造成大量的人力物料浪費。

國內外研究輥壓機整機的仿真還很少,主要針對機床和加工中心[1-3],或針對軋輥與被軋物之間的局部作用過程[4-7]。傳統輥壓機的剛度相對被軋物剛度要大很多,整機可以看作剛體不變形進行研究；而對于極片軋制,整機變形量對于其表面一致性和材料的壓實密度有很大的影響,直接影響電池的性能。針對軋制對象的復雜性和工藝參數的控制要求,本文對鋰電池極片輥壓機軋制過程進行建模仿真和分析,建立整個軋制系統輥壓力與實際極片壓縮量之間的關系，為定量控制極片制造工藝參數提供保證；同時采用仿真驅動設計的方式，對整機進行建模優化，以提高輥壓機設備的設計生產效率。

1　極片壓縮與輥壓機變形關系

對鋰電池極片進行仿真分析,需要建立極片壓縮比、輥壓力與雙輥輥縫之間的數值關系,這樣才能夠定量地控制極片輥壓過程的工藝參數。整個輥壓機主機主要包括：輥系、軸承、軸承支座、機架、液壓缸和調整輥縫大小的楔形塊以及連接機構。

圖1所示是以極片理想壓縮量Δxi為輸入、極片實際壓縮量Δxo為輸出時系統的數學模型,其傳遞函數如下：

(1)

式中，G1為極片的壓縮比與輥壓力之間的關系系數；G2為輥子剛度；K1、Ka分別為機架、軸承剛度。

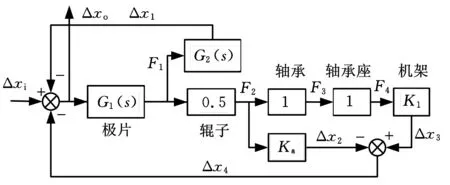
圖1　輥壓機系統方塊圖

圖1中，F1～F4為各模塊之間傳遞的力關系,Δx1～Δx4為各模塊之間傳遞的位移變形關系。

由于輥壓機的輸入轉速慢、工作狀態較為平穩，故可以將工作過程看作靜態進行分析。在靜態力學分析時，輥壓力通過軋輥、軸承、軸承座，最終傳遞到機架上。通過求解G1、G2、K1和Ka即可定量求出Δxo。

1.1輥壓機數學模型

1.1.1軸承剛度等效

滾動軸承的剛度一般可定義為軸承內外套圈產生單位的相對彈性位移量所需的外加負荷。滾動軸承的滾子與滾道之間的接觸看成純粹的Hertz接觸。計算軸承軸向剛度ka和徑向剛度kr的經驗公式[8]為

(2)

(3)

其中,Fa為軸承承受的軸向力，Fr為承受的徑向力，其他符號解釋見表1。型號LDHY600-N60的輥壓機采用四列向心短圓柱滾子軸承,其等效參數取值見表1。計算得到的整個軸承徑向剛度為20 073N/mm，軸向剛度為7062N/mm。有限元分析時軸承使用圓周相位差120°的三個彈簧并聯等效。

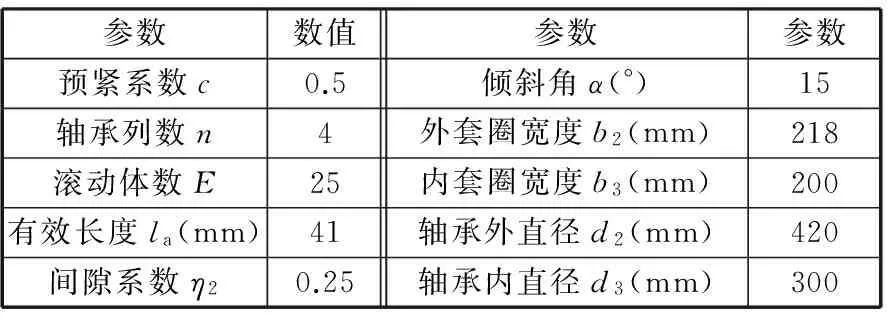
表1　軸承等效參數

1.1.2整機有限元分析結果

輥壓機生產線結構復雜,建立仿真模型時只考慮主機部分,輥壓機系統由機架、軋輥、液壓油缸、楔塊、軸承及軸承座等部件組成。輥壓機機架材料為45鋼，上下軋輥材料為9Cr2Mo，上下軸承座材料為ZG45，其他零部件材料為45鋼。劃分網格時選擇四面體單元自由劃分，有限元模型如圖2所示，模型中共有節點134 160個，單元55 325個。

圖2　整機有限元模型

有限元分析時將機架底面固定,在兩個下軸承座上分別施加250～1500 kN作用力,在安裝液壓缸的機架上相應地施加反向作用力；在上下軋輥與極片接觸的7 mm寬的窄帶上施加1000 kN的作用力,模擬極片受到的輥壓反作用力。載荷的位置與實際工作情況對應,得到整機載荷與圖2標示位置變形之間的關系,如圖3所示。

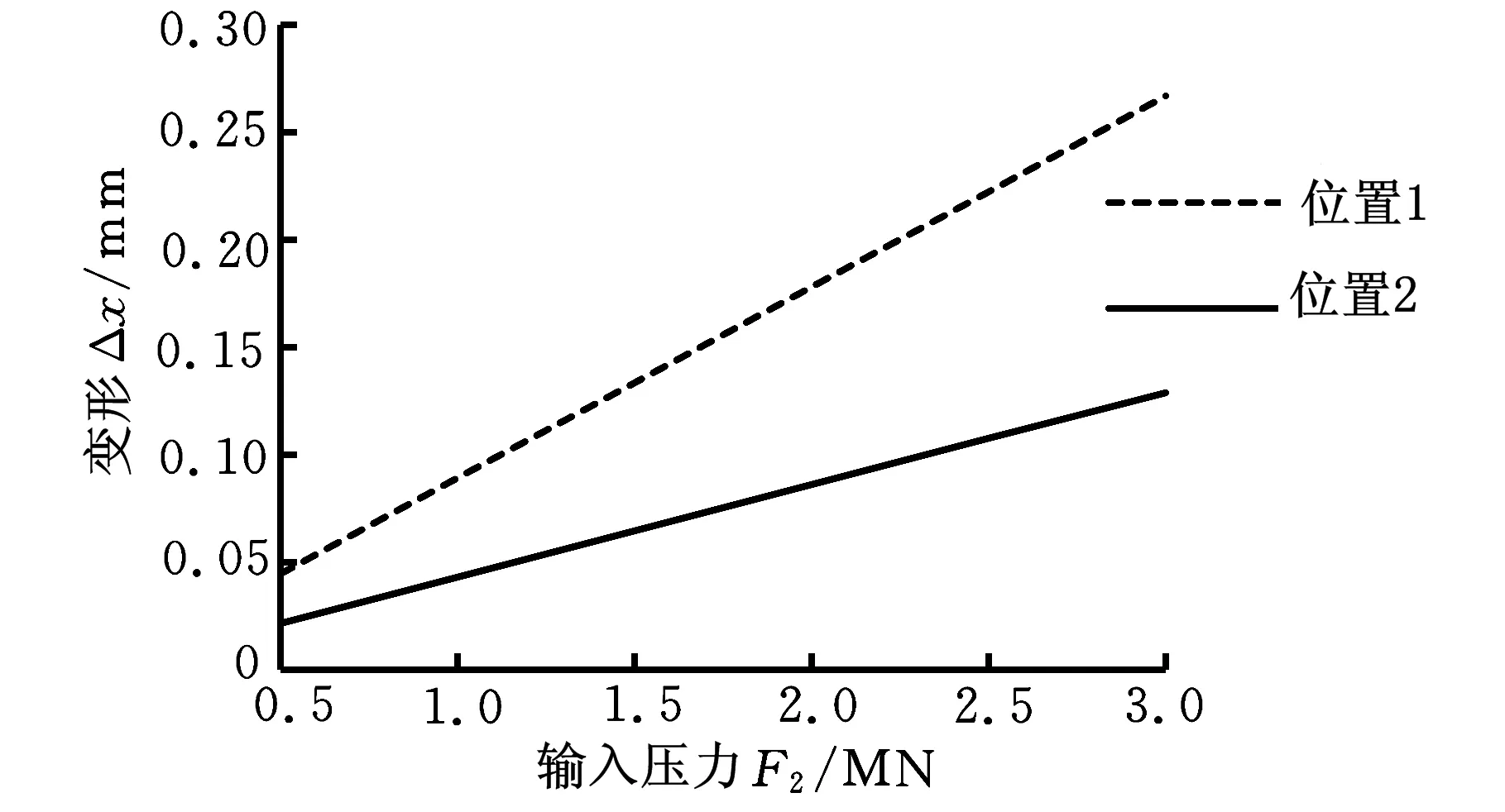
圖3　數字模型的測試點變形

1.1.3整機試驗結果

對同型號輥壓機進行變形測試試驗。在物理樣機同圖 2的位置上安裝千分表。液壓缸逐步加載6組試驗壓力得到不同測試點的位移形變,如圖4所示。比較物理樣機和數字模型之間在變形量上的結果偏差,如表2所示。

圖4　物理樣機測試點變形

位置輸入壓力(kN)500100015002000250030001(%)11.411.427.222.727.030.12(%)13.513.429.625.026.132.5

Zhang等[9]研究表明固有頻率是驗證數字模型準確性的一個重要指標。對輥壓機進行模態實驗,用激振器從不同方向對整機進行激振,激振信號為正弦掃頻,掃頻范圍為30～500 Hz，處理得到拾振點所測的加速度信號頻響函數，與數字模型的仿真固有頻率進行對比,得到如表3所示的結果。由于在有限元模型中存在一部分連接被定義為剛性,因而整機固有頻率的仿真值大部分較試驗值略大。所建立的數學模型與實際情況比較吻合，說明上述數字模型可以代替物理樣機進行試驗分析和設計優化。

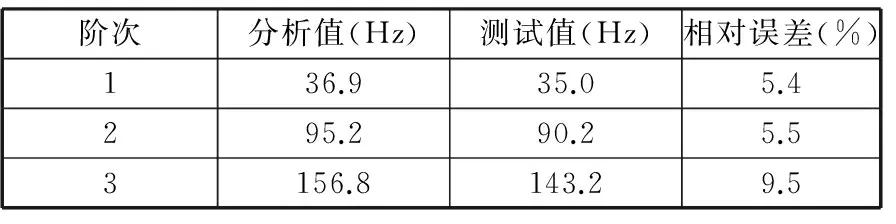
表3　輥壓機固有頻率有限元分析值與測試值

1.2極片“輥壓力-壓縮量”關系

金屬輥壓工藝常被視為短暫的彈塑性變形過程,而極片這種在基體上涂覆多種化合物材質的壓縮變形情況要復雜得多，此處簡單地抽象為5個階段:①“坍塌”期，從極片接觸輥面開始，至極片內部的孔洞被填補完為止;②初步壓縮期,坍塌結束后，微粒團間相互發生碰撞和擠壓;③劇烈壓縮期，極片內各微粒團繼續向輥縫中心運動，直至輥縫最小處，微粒團相互劇烈擠壓，發生形變甚至破壞，隨著壓力的增加，長鏈的粘結劑會打開甚至斷裂，從而影響電芯的循環性能;④受控恢復期，從輥縫最小處開始，所受壓力不斷減小，極片發生一定程度的恢復;⑤自然恢復期,極片脫離輥面，在自身新彈性系數下進行恢復。

極片輥壓微觀變形情況復雜,甚至在表面附近有一層大致5 μm的致密層。為保證孔洞的坍塌效應得到體現,此處采用粉末冶金材料等效極片涂覆材料。粉末冶金材料由于內部孔隙的存在,在塑性變形時除形狀變化外還伴有體積的變化。因為其屈服應力除了與應力偏量有關外，還和靜水應力有關，因此Mises屈服準則對粉末冶金材料不再適用。此處在“可壓縮連續體”的假設上,使用Gurson[10]模型定義粉末冶金材料的屈服條件,即：

(4)

式中,q為有效Mises應力;p為靜水壓強;σy為全密度材料的屈服應力;γ為空穴體積比。

對于錳酸鋰(LiMn2O4)涂覆的正極電池極片,其仿真等效參數值為：密度1120 kg/m3、相對密度0.4、彈性模量15 GPa、泊松比0.3、屈服強度16.872 MPa。

1.3軋制過程“輥壓力-壓縮量”關系

通過上述假設得到極片“輥壓力-壓縮量”之間的關系,這里的輥壓力并不是實際作用在軋輥上力的大小。借鑒冷軋薄材的軋制力計算數學模型,如柯夫冷軋軋制力公式、斯通平均單位壓力模型、Bland-Ford-Hill顯隱式模型、Bryant和Roberts單位寬度模型[11]等，可以獲得軋制過程中的輥壓力。假設軋制過程中極片厚度、前后張力、軋輥轉速以及溫度等恒定不變，只考慮極片出口厚度的變化，可得到輥壓力[12]為

(5)

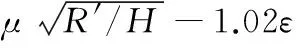
(6)

根據已建立的有限元模型,得到不同輸入壓力(50～300kN)下的“輥壓力-輥縫”關系,對應圖5中平行的斜線組；根據上述假設建立的極片“輥壓力-縮量”關系,對應圖5中壓縮量曲線。由于輥縫變形量Δ1和極片壓縮量Δxo之間存在Δ1+H0=0.2-Δxo的關系(H0為初始輥縫),因此,隨H0的增加,圖5中極片壓縮量曲線向下平移。兩種曲線的交點即為零輥縫下對應輸入壓力下輥壓機作用于極片的輥壓力,并可通過輥縫變化量間接得到實際極片的壓縮量。圖5對于指導輥壓極片生產過程具有重要意義。在給定輥縫、保證極片壓縮比的條件下，確定液壓缸應提供的輸入壓力,從而有效地控制輸入能源的量值。

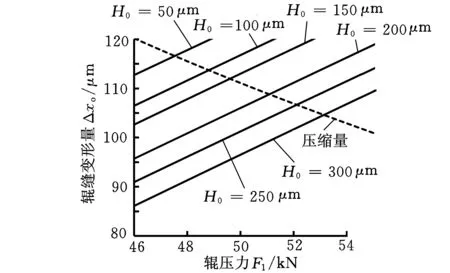
圖5　整機系統“輥壓力-壓縮量”關系

2　輥壓機設計優化

設計的不合理會造成整機剛度降低，進而影響極片的加工精度和生產效率。如果每個設計參數各個候選取值對結果產生的影響均通過仿真進行分析，則計算量巨大，而且不能確定每個參數對結果的影響程度，更難以尋找最優解。本節以輥縫變形量最小為目標，對各設計參數進行優化。

2.1基于響應面法的優化流程

響應面法(response surface methodology,RSM)是基于試驗結果建立因素與指標的關系模型[13]。已有許多研究基于響應面開展了設計優化[14-15]。基于響應面法的優化設計步驟見圖6。

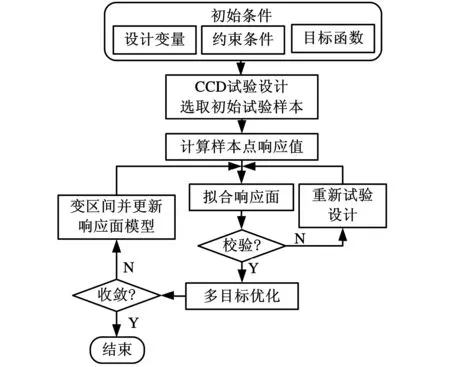
圖6　基于響應面法的輥壓機優化設計流程

(1)確定設計變量及設計目標。選取影響輥壓機整機剛度的重要參數作為設計變量,以減小輥縫變形量作為優化目標。

(2)構建響應面模型并檢驗模型的準確性。設計變量和目標確定后，使用中心復合設計(central composite design,CCD)進行試驗設計,得到不同設計變量值的組合以及相應的目標結果。運用最小二乘法獲得目標函數的二次響應面近似模型：

(7)

其中,z為輸出目標,yi為設計變量,m為設計變量的個數,βi j為待定系數,υ為誤差;為檢驗響應面的精確性,對試驗設計得到的近似模型的近似值做擬合度檢驗。若校驗通過,可利用該二次響應面近似模型進行優化,反之須重新設計試驗。

(3)基于響應面模型進行優化并驗證結果。利用滿足精度要求的響應面近似模型代替真實的有限元模型進行優化,獲取優化值,其數學模型為

(8)

其中,fi(X)為要考察的目標,gk(X)與hl(X)為約束。采用非支配排序遺傳算法Ⅱ(NSGA-Ⅱ)對該模型進行求解。

2.2輥壓機主機結構優化

按照上述設計優化流程,對輥壓機的機架部分進行優化,除軋輥定制參數外的其他參數隨著設計變量的改變而變化。分別選取機架高度y1、機架寬度y2、機架厚度y3、液壓缸輸入壓力y4和輥縫之間的壓力y5為優化變量,對應的初值分別為1976 mm、1097 mm、196 mm、9.53 MPa和1000 kN。其中前三個參數為設計優化參數,指導整機設計研發過程;后兩個為工藝優化參數,指導輥壓極片過程控制。設計五因素CCD,獲取27個樣本點。將輥縫變形量z作為研究對象,得到輥縫的試驗結果見表4。

表4　CCD和試驗結果

根據最小二乘擬合得到二次多項式響應面,表達式為

z=0.0348-0.0770y1-0.3421y2+0.2574y3-

10-4y1y4+0.0156y1y5+0.0033y2y3+

0.0037y2y4+0.0673y2y5+1.70×10-5y3y4-

0.0011y3y5-1.49×10-5y4y5

為驗證二次多項式擬合方程顯著性,進行擬合度檢驗。擬合度檢驗值為13.26,大于F0.02(21,5)=6.99,結果表明回歸方程擬合得較好。

由圖7可以觀察到不同因素間的交互影響對輥縫變化的影響趨勢,也可以方便觀察到使輥縫變形量最優時各因素的取值范圍。圖7a顯示隨著機架橫梁升高和寬度的增加,整機剛度增加,輥縫變形越來越小,y1對于輥縫變形的影響比較強烈。圖7b則是機架寬度y2與y3聯合作用對于輥縫變形量的影響。液壓缸輸入壓力y4和輥縫之間的壓力y5對于結果的變形量影響是負相關的,輥縫變形隨著兩者的增加而等比例增大。

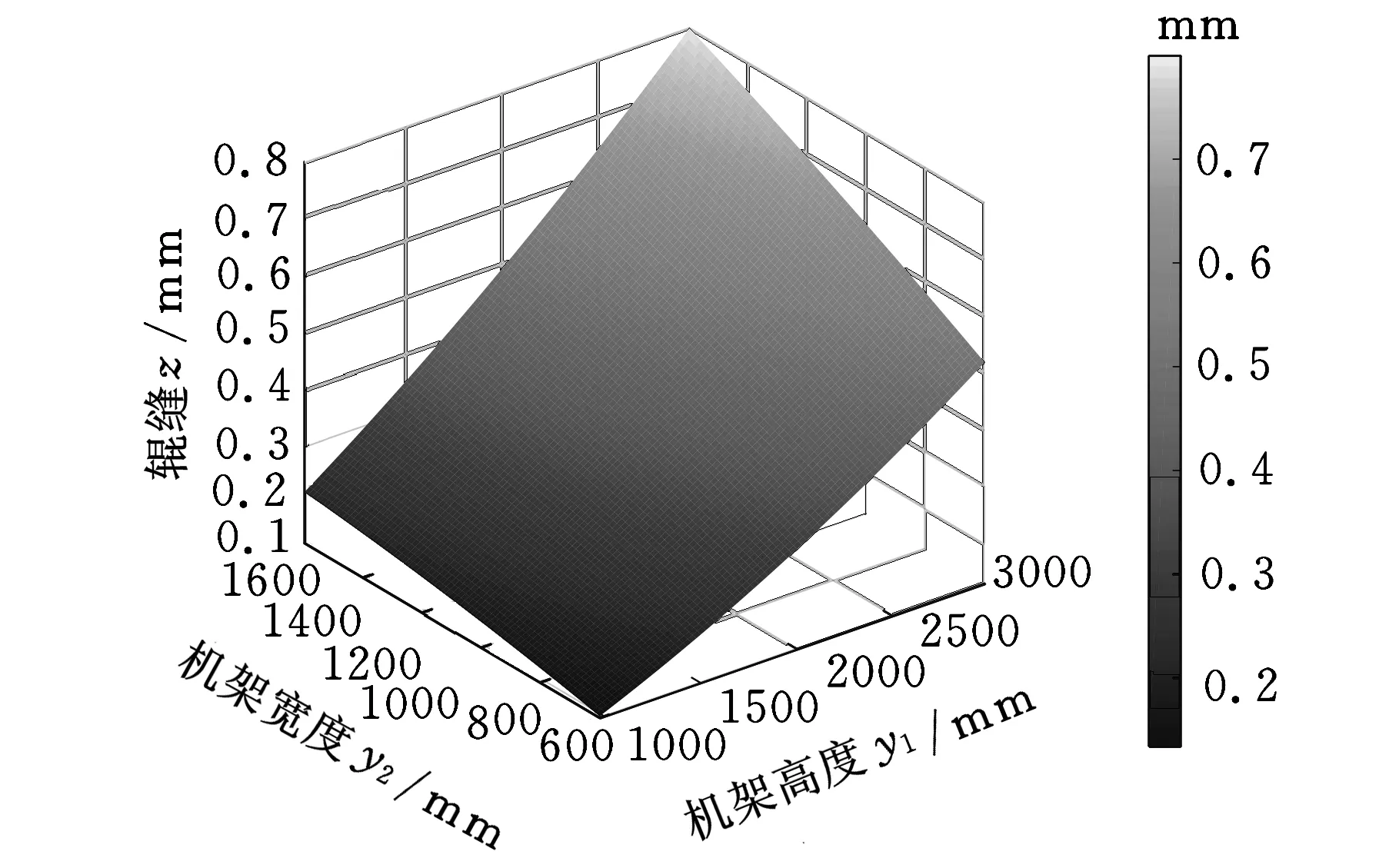
(a)y1與y2交互曲面

(b)y2與y3交互曲面圖7　不同設計參數的二次響應面

通過NSGA-Ⅱ計算,輥縫變形量最小的三個設計結果如表5所示。優化結果可以在保證輥縫變形量最小和整機剛度的前提下,得到最省材料的設計結果和最省能源的工藝生產方式。以候選優化結果1為例,相較于原型機在質量上減小了15.0%,而載荷值減小了74.9%;由于輥縫之間的壓力也減小了,故該優化結果可以用于加工材質較軟的陽極極片。

表5　整機優化結果

3　結論

(1)建立了輥壓機整機的有限元模型。試驗驗證了該模型與實際輥壓機物理模型結果基本一致，可代替物理樣機進行系統分析。

(2)將有限元方法引入到極片軋制過程的分析中,對涂覆層力學參數進行預測。根據仿真得到的輥壓機整機“輥壓力-輥縫變形”關系與極片的“輥壓力-壓縮量”關系可以實現定量控制極片軋制厚度。

(3)對有限元模型進行基于響應面的分析,得到整機主要設計參數之間的定量關系,同時得到多目標優化結果,為后續輥壓機設計提出改進方向,有利于迅速開展產品設計和分析。

[1]孫明楠,殷國富,胡騰,等.基于廣義動態信息模型的機床結合部動剛度參與因子辨識方法[J].機械工程學報,2013,49(11):61-69.

Sun Mingnan, Yin Guofu,Hu Teng,et al.Method of Dynamic Stiffness Participation Factors Identification of Machine Tool Joints Based on the Generalized Dynamic Information Model[J]. Chinese Journal of Mechanical Engineering,2013,49(11):61-69.

[2]李殿新,趙沿民,張建富,等.立式加工中心靜剛度細化試驗與有限元分析[J].農業機械學報,2012,43(12):262-267.

Li Dianxin,Zhao Yanmin,Zhang Jianfu,et al.Fine Experiment and Finite Element Analysis for Static Stiffness of Vertical Machining Center[J].Transactions of the Chinese Society for Agricultural Machinery,2012,43(12):262-267.

[3]彭艷華,管貽生,張憲民,等.基于復合優化方法立式數控加工中心的多目標優化設計[J].振動與沖擊,2012,31(6):48-52.

Peng Yanhua,Guan Yisheng,Zhang Xianmin,et al.Multi-objective Optimization Design for a Vertical Machining Center Based on Composite Optimization Method[J].Journal of Vibration and Shock,2012,31(6):48-52

[4]劉浩然,侯東曉,時培明,等.軋機輥系滯后非線性垂直振動系統的振動特性[J].機械工程學報,2011,47(13):65-71.

Liu Haoran,Hou Dongxiao,Shi Peiming,et al.Vibration Characteristics of Hysteretic Nonlinear Vertical Vibration System of Rolling Mill Roller[J]. Chinese Journal of Mechanical Engineering,2011,47(13):65-71.

[5]甘建國.高壓對輥粉碎的微分剪切理論及數學模型[J].機械工程學報,2008,44(3):241-248.

Gan Jianguo.Differential Shear Theory and Mathematical Model of High Pressure Double Roll Crush[J].Chinese Journal of Mechanical Engineering,2008,44(3):241-248.

[6]Niroomand M R,Forouzan M R,Salimi M,et al.Experimental Investigations and ALE Finite Element Method Analysis of Chatter in Cold Strip Rolling[J].ISIJ International,2012,52(12):2245-2253.

[7]王東城,彭艷,劉宏民.冷軋帶鋼平整機高精度高速度軋制力模型開發[J].塑性工程學報,2008,15(1):172-177.

Wang Dongcheng,Peng Yan,Liu Hongmin.A High-resolution High-speed Rolling Force Model for Cold Strip Temper RollingMill[J].Journal of Plasticity Engineering,2008,15(1):172-177.

[8]機床設計手冊編寫組.機床設計手冊[M].北京:機械工業出版社,1979.

[9]Zhang G P,Huang Y M,Shi W H,et al.Predicting Dynamic Behaviours of a Whole Machine Tool Structure Based on Computer-aided Engineering[J]. International Journal of Machine Tools & Manufacture,2003,43(7):699-706.

[10]Gurson A L. Continuum Theory of Ductile Rupture by Void Nucleation and Growth:Part I-Yield Criteria and Flow Rules for Porous Ductile Materials[J].Journal of Engineering Materials and Technology,1977,99(1):2-15.

[11]采利科夫.軋鋼機的力參數計算理論[M].北京:中國工業出版社,1965.

[12]楊節.軋制過程數學模型[M].北京:冶金工業出版社, 1993.

[13]何為.優化試驗設計方法及數據分析[M].北京:化學工業出版社,2012.

[14]馬勁紅,張文志,宋劍鋒,等.MOGA和FEM相結合實現萬能型鋼軋機機架圓角的多目標優化[J].塑性工程學報,2008,15(1):146-149,177.

Ma Jinhong,Zhang Zhiwen,Song Jianfeng,et al.Multi-objective Optimization of the Housing’s Fillet Angle of the Universal Rolling Mills using MOGA Combined with FEM[J].Journal of Plasticity Engineering,2008,15(1):146-149,177.

[15]于海蓮,王永泉,陳花玲,等.響應面模型與多目標遺傳算法相結合的機床立柱參數優化[J].西安交通大學學報,2012,46(11):80-85.

Yu Hailian,Wang Yongquan,Chen Hualing,et al.Optimization for Machine Tool Column Combining Response Surface Model with Multi-objective Genetic Algorithm[J].Journal of Xi’an Jiaotong University,2012,46(11):80-85.

(編輯袁興玲)

Stiffness Analysis and Structure Optimization of Rolling Mill for Lithium-ion Battery Electrode Manufacturing

Ma Songhua1Tian Ling2

1.Shandong University,Jinan,2500132.Tsinghua University,Beijing,100084

In the process of rolling electrodes,due to the contradiction between the energy density and the material mechanical properties of coatings on the electrode,the roller pressure should be controlled strictly according to the compression ratio.Actually,the roller surface made the gap between two rollers difficult to measure through experiments.Consequently,it was difficult to directly quantify the relation between the gap size and roller pressure by using physical prototype.The variations of physical quantities during the electrodes manufacturing process were simplified to build the digital model of rolling mill and electrode deformation.With the help of the digital model,the relation of gap variation and pressure was quantitatively simulated.According to the above study, on the purpose of simulation-driven design,the structural parameters and work condition of digital rolling mill were optimized by the response surface methodology and multi-objective genetic optimization algorithm.The stiffness test has validated the digital model and the simplification hypothesis.These results are important to lay a plan for rolling processes;meanwhile the research and development efficiency is improved by the response surface-based design optimization.

rolling mill;lithium-ion battery electrode;finite element analysis;optimization design

2013-08-20

國家自然科學基金資助項目(51175287)

TG333.1;TB472DOI：10.3969/j.issn.1004-132X.2015.06.018

馬嵩華,女,1985年生。山東大學機械工程學院助理研究員。主要研究方向為協同設計、知識工程。發表論文8篇。田凌,女,1963年生。清華大學機械工程系教授、博士研究生導師。