圓柱正弦活齒傳動扭轉振動系統剛度研究

周思柱　曾運運　袁新梅

長江大學，荊州，434000

圓柱正弦活齒傳動扭轉振動系統剛度研究

周思柱曾運運袁新梅

長江大學，荊州，434000

針對圓柱正弦活齒傳動過程中的受力情況,基于彈性小變形和變形協調假設,提出了理論狀態下嚙合作用力分析模型；根據赫茲理論和嚙合副的幾何關系，建立了嚙合副的嚙合剛度模型，推導出接觸點處主曲率和嚙合副嚙合剛度計算公式；依據能量不變原理建立了系統扭轉振動模型，給出了等效扭轉剛度計算公式，形成了一套完整的系統剛度矩陣計算分析方法;結合具體實例進行了分析,發現該扭轉振動是一個時變系統且系統剛度矩陣呈現周期分布的特點，求出了周期計算公式，并提出了兩種簡化求解該扭轉振動系統固有頻率的方法。分析結果可作為圓柱正弦活齒傳動機構的結構設計、振動分析的基礎。

圓柱正弦活齒傳動；嚙合力；嚙合剛度；等效扭轉剛度；系統剛度矩陣

0　引言

圓柱正弦活齒傳動是一種用來傳遞同軸間運動和動力的新型活齒傳動機構,它具有結構緊湊、傳動比大且范圍廣、承載能力強、傳動效率高等優點，是一種很有發展前景的新型傳動機構。目前對圓柱正弦活齒傳動的研究主要集中在圓柱正弦活齒傳動的嚙合原理、傳動比、運動學、滑動率、活齒受力、模糊故障樹等方面[1-4],而關于圓柱正弦活齒傳動的動力學方面的研究很少見報道，特別是嚙合副嚙合剛度、系統剛度矩陣方面的研究極少。

本文以圓柱正弦活齒傳動系統為研究對象，建立了一套完整的圓柱正弦活齒傳動扭轉振動系統剛度矩陣計算分析方法，發現了該扭轉振動系統時變性和周期性的特點，提出了兩種振動系統固有頻率簡化求解方法。

1　活齒受力分析

圓柱正弦活齒傳動由主動軸、殼體、活齒架及活齒4部分組成，如圖1所示。殼體內圓柱表面上有周期數為Z3的內正弦滾道，主動軸外圓柱表面上有周期數為Z1的外正弦滾道，在內滾道、外滾道以及活齒架槽的交錯區域安裝有球形活齒。由于內外滾道均具有周期性，每個活齒與正弦滾道間共軛齒廓的工作過程又完全相同，因此在活齒受力分析時可以選取任意活齒為研究對象。

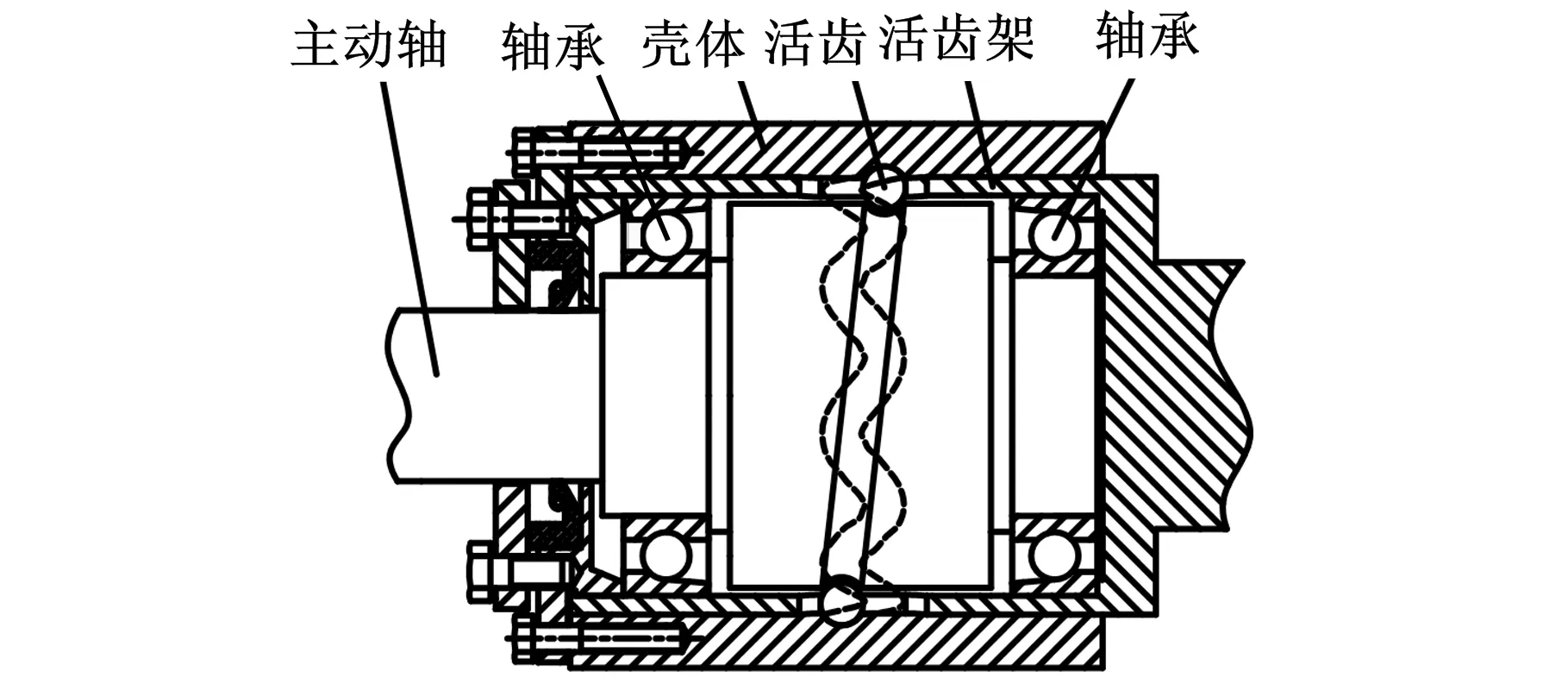
圖1　圓柱正弦活齒傳動結構圖

為了便于分析并使問題簡化，做如下假設[5]：①各構件無制造誤差，整機無裝配誤差；②活齒與主動軸、活齒架及殼體嚙合副之間為接觸彈性小變形；③活齒的質量相對較小，忽略其慣性力；④不考慮嚙合副各元素之間的摩擦力。

1.1活齒受力平衡方程

活齒局部坐標系為Oxyz,坐標原點O為活齒的球心,x軸表示活齒傳動的徑向方向,y軸表示活齒傳動的周向方向,z軸表示活齒傳動軸向方向。設活齒在運動時處于平衡狀態，受力如圖2所示,根據各個力的空間平衡關系有

(1)

式中,F1i為主動軸對活齒i的接觸力;α1i為主動軸對活齒i的作用力接觸角;μ1i為主動軸與活齒i嚙合副接觸線方向角;F2i為活齒架對活齒i的接觸力;F3i為殼體對活齒i的接觸力;α3i為殼體對活齒i的作用力接觸角;μ3i為殼體與活齒i嚙合副接觸線方向角。

圖2　活齒空間受力圖

1.2變形協調方程和幾何方程

主動軸與活齒i之間的接觸力F1i可以分解為徑向力F1xi和徑向法截面方向的力F1yzi。假定主動軸瞬時不動，給活齒施加一個順時針方向的力矩T，在該力矩的作用下，各活齒與主動軸接觸處產生接觸變形，使活齒中心轉過一個角度Δφ,則所有活齒中心相應地發生一個相同的微小的周向位移Δs。根據主動軸正弦滾道與活齒的嚙合方程可知,主動軸與活齒i嚙合副接觸線方向角為

μ1i=arctan(-R1/(AZ1cos(Z1φ1i)))

式中,φ1i為活齒i相對主動軸轉角；R1為主動軸空間正弦曲線徑向半徑；A為內外正弦滾道幅值。

由變形協調條件,假設Δs在F1yzi方向的投影大小與F1yzi成正比例[3],即F1yzi∝Δscosμ1i,則有如下等式成立：

(2)

μ1max=arctan(R1/(AZ1))

對主動軸列扭矩平衡方程，則

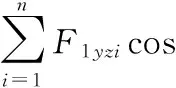
(3)

式中，n為活齒個數；Tin為輸入扭矩。

將式(2)代入式(3)可得

(4)

將式(4)代入式(2)可得

(5)

利用平均法可以求得

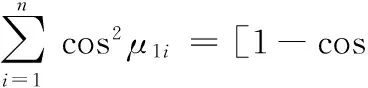
根據活齒i嚙合副幾何關系可知

(r1-r)(cosα1i-cosα3i)=R1-R3

(6)

式中,r為活齒半徑;r1為正弦滾道半徑;R3為殼體空間正弦曲線徑向半徑。

2　嚙合副嚙合剛度方程

研究分析圓柱正弦活齒傳動的嚙合剛度,先作如下假設[6-8]:①各零件的加工、裝配準確，裝配間隙為零，無間隙嚙合;②嚙合面上的摩擦力忽略不計;③主動軸、活齒、殼體、活齒架有變形，其變形量為微小數量級，可以忽略。

根據微分幾何理論，設曲面上一個非臍點，其法曲率隨切矢方向的改變而改變，在不同方向的法曲率中總存在最大值和最小值，這兩個最值稱為主曲率，其對應的方向稱為主方向，并且兩個主方向相互垂直[9]。根據主動軸滾道面與活齒i幾何關系可知,在其接觸點處四個主曲率分別為

(7)

式中,R為活齒中心旋轉半徑。

同理,可知活齒i與殼體滾道面在接觸點處四個主曲率分別為

(8)

活齒與主動軸滾道面，或活齒與殼體滾道面和活齒與活齒架槽面彈性接觸問題，均可看作為兩個自由曲面體彈性接觸問題[10]。由此可知,彈性壓縮變形引起的相對位移量為

(9)

式中，F為兩接觸點法向壓力；a為接觸橢圓的長半徑；J為橢圓積分；E1、E2及ν1、ν2分別為材料彈性模量和泊松比。

當兩彈性體均是鋼，彈性模量E1=E2=210 GPa、泊松比ν1=ν2=0.3時，式(9)可以簡化為

(10)

其中，∑ρ為主曲率和，且∑ρ=ρ11+ρ12+ρ21+ρ22。

由嚙合剛度的定義,對式(10)兩邊同時對δF求導,可得嚙合剛度：

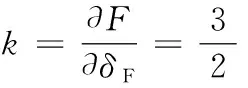
(11)

3　圓柱正弦活齒傳動扭轉振動

3.1扭轉振動模型建立

根據圓柱正弦活齒傳動的結構特點,作如下假設[11]:①因殼體與機架固聯，不考慮其振動；②不計軸承支撐剛度、主動軸及活齒架的彎曲剛度；③不考慮摩擦和重力的影響。

將圓柱正弦活齒傳動簡化為主動軸、活齒、活齒架和殼體四個部分，按照集中參數法對主要運動構件作如下處理：

(1)主動軸等效為兩個慣性圓盤M11、M12,且將主動軸轉動慣量平均分配給兩個慣性圓盤。

(2)活齒架等效為兩個慣性圓盤M31、M32,且將活齒架轉動慣量平均分配給兩個慣性圓盤。

(3)所有活齒作為一個整體構件進行研究，該構件視為慣性盤圓M2。

(4)主動軸-活齒嚙合副變形、活齒-活齒架嚙合副變形、活齒-殼體嚙合副變形分別視為扭轉彈性體。

根據上述方法，可以將圓柱正弦活齒傳動化簡為一個串聯傳動系統，為了進一步化簡系統，利用動能和勢能不變原則，將各剛性圓盤和彈性軸轉換到主動軸上，構成單一軸線的五自由度扭轉振動模型，如圖3所示。圖3中，kin、cin為主動軸扭轉剛度和扭轉阻尼；k1e、c1e為主動軸與活齒嚙合副總等效扭轉剛度和總等效扭轉阻尼；M2e為所有活齒總等效轉動慣量；k2e、c2e為活齒與活齒架嚙合副總等效扭轉剛度和總等效扭轉阻尼；M31e、M32e為活齒架等效轉動慣量；k3e、c3e為活齒與殼體嚙合副總等效扭轉剛度和總等效扭轉阻尼;kout、cout為活齒架扭轉剛度和扭轉阻尼；Tout為輸出扭矩。

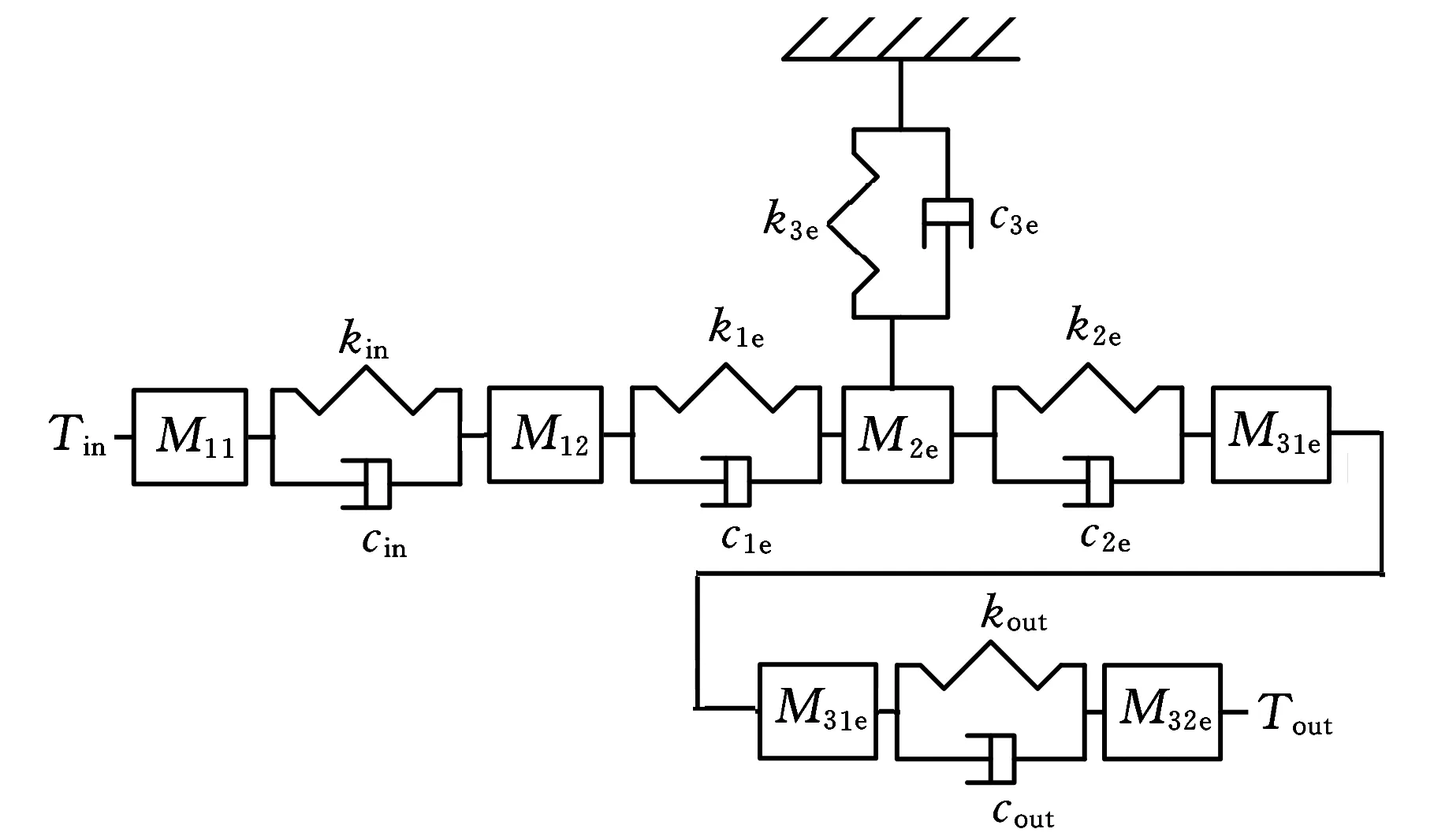
圖3　圓柱正弦活齒傳動扭轉振動模型

3.2等效扭轉剛度計算

根據扭轉動力學模型得到扭轉振動系統剛度矩陣K為

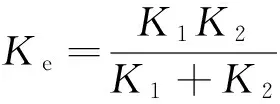
要建立主動軸上的當量盤-扭轉彈簧的系統動力學模型,應求解各嚙合剛度在輸入軸上的總等效扭轉剛度。由于各個單齒嚙合副嚙合剛度是轉角的函數，不能簡單地疊加，故先分別求解單齒嚙合剛度的等效扭轉剛度，然后求出所有嚙合副的總等效扭轉剛度。

3.2.1主動軸與活齒嚙合副總等效扭轉剛度

對于活齒與主動軸正弦滾道的嚙合副來說，當主動軸轉過角位移Δφ時,主動軸與活齒i接觸點作用力的方向上產生的線位移為

xi=R0Δφsinα1icosμ1i

(12)

式中,R0為主動軸半徑。

按照等效前后系統勢能不變原則，利用下式可以求得全部活齒與主動軸總等效扭轉剛度：

(13)

式中,k1i為主動軸與活齒i嚙合剛度。

將式(12)代入式(13)可得

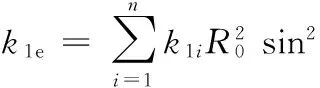
(14)

3.2.2活齒與殼體嚙合副總等效扭轉剛度

對于活齒與殼體正弦滾道的嚙合副來說,當主動軸轉過角位移Δφ時,活齒i與殼體接觸點作用力的方向上產生的線位移為

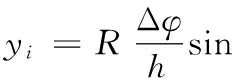
(15)

式中,h為傳動比。

按照等效前后系統勢能不變原則,利用下式可以求得全部活齒與殼體總等效扭轉剛度:

(16)

式中，k3i為活齒i與殼體嚙合剛度。

將式(15)代入式(16)可得

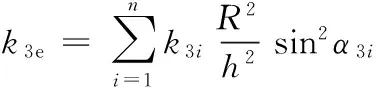
(17)

3.2.3活齒與活齒架嚙合副總等效扭轉剛度

對于活齒與活齒架的嚙合副來說,當主動軸轉過角位移Δφ時,活齒i與活齒架接觸點在作用力方向上產生的線位移為

(18)

按照等效前后系統勢能不變原則,利用下式可以求得全部活齒與殼體總等效扭轉剛度:

(19)

式中,k2i為活齒i與活齒架嚙合剛度。

將式(18)代入式(19)可得

(20)

4　等效扭轉剛度計算實例與分析

上述研究表明，系統中活齒與主動軸、活齒架、殼體的嚙合剛度k1i、k2i、k3i是活齒嚙合位置的函數,所以系統的剛度矩陣K也是活齒嚙合位置的函數，因此圓柱正弦活齒傳動扭轉振動是一個5自由度的二階變系數線性系統。

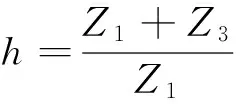
圖4　嚙合副嚙合力變化曲線

將5個活齒嚙合副嚙合力分別代入式(11)，就可求出各個活齒在不同位置時的嚙合副剛度。篇幅限制，只繪制了1個活齒嚙合副嚙合剛度隨主動軸轉角變化曲線，如圖5所示,圖中,k1為主動軸與活齒之間嚙合剛度,k2為活齒與活齒架之間嚙合剛度;k3為活齒與殼體之間嚙合剛度。

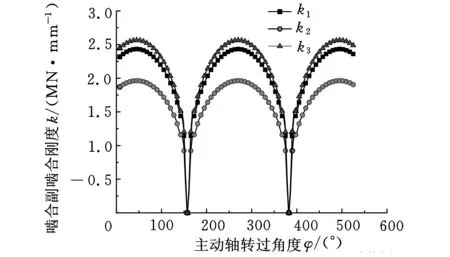
圖5　嚙合副嚙合剛度變化

將各嚙合副嚙合剛度分別代入式(14)、式(17)、式(20)，就可求出活齒在不同位置時的嚙合副總等效扭轉剛度。本文只列出了一部分數據和繪制了主動軸與活齒嚙合副總等效扭轉剛度變化曲線，如表1、圖6所示。

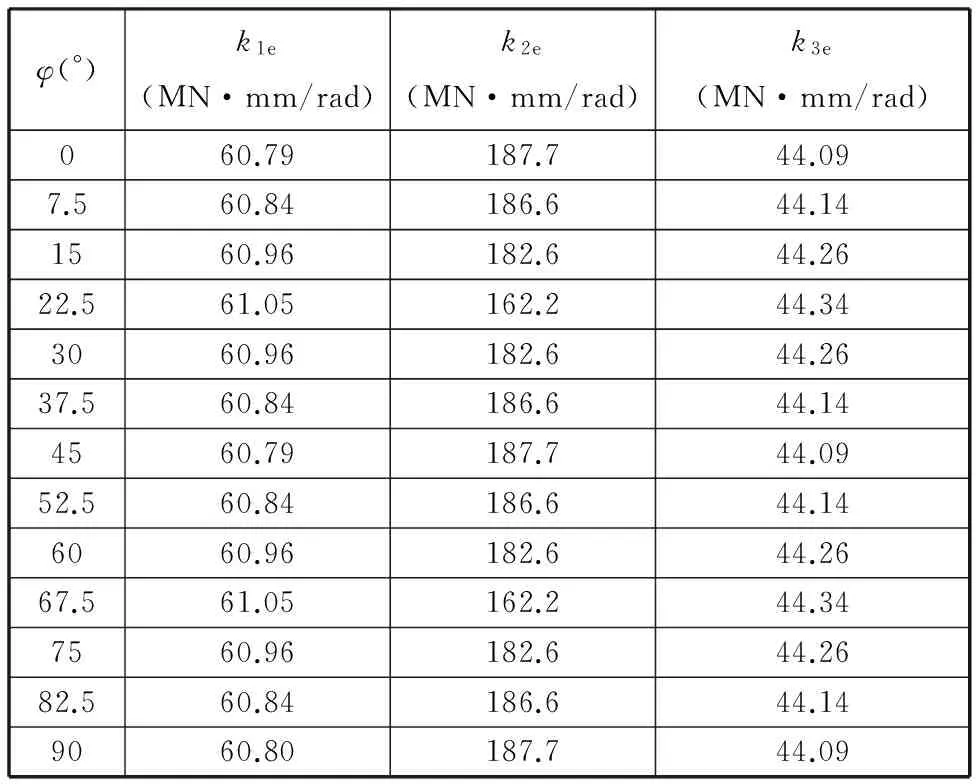
表1　嚙合副總等效扭轉剛度

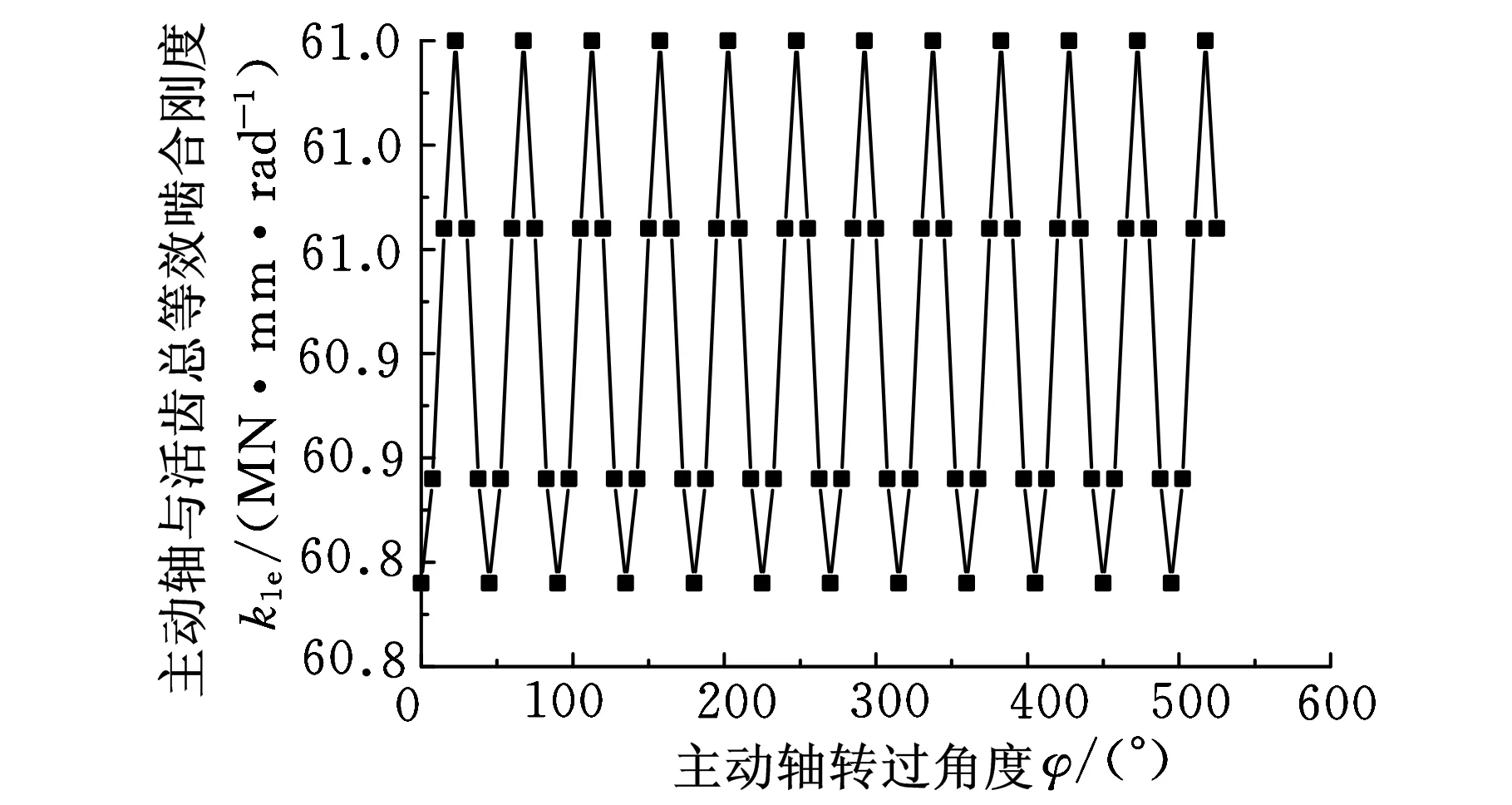
圖6　主動軸與活齒嚙合副總等效扭轉剛度曲線

分析表1和圖6可以發現，該實例嚙合副等效扭轉剛度k1e、k2e、k3e均呈現周期性，且周期相同，均為45°，這與理論分析結果一致。在一個周期內，嚙合副等效扭轉剛度變化范圍很窄。現將k1e、k2e、k3e代入到扭轉振動系統剛度矩陣K中，可以發現系統剛度矩陣也呈現周期性，周期TK=45°。

圓柱正弦活齒傳動二階時變扭轉振動系統的剛度矩陣具有周期性，其周期TK=πh/(Z3n),即結構參數決定了周期大小，原因是圓柱正弦活齒傳動結構具有周期性。分析發現，該扭轉振動系統的質量矩陣M不變。扭轉振動系統可認為是經典阻尼系統，則該扭轉振動系統的阻尼矩陣C=αM+βK,其中,α、β是實常數。通過上述分析可知，阻尼矩陣C也呈現周期性，其周期TC與剛度矩陣周期TK相同。

對扭轉振動系統固有頻率進行分析可以避免系統共振，為該傳動系統的動態響應分析以及動載荷的分析計算提供理論數據。質量矩陣M不變，剛度矩陣K和阻尼矩陣C具有相同的周期，所以系統的固有頻率隨活齒嚙合位置的變化周期性地變化，且周期與剛度矩陣的周期TK相同。該結論與文獻[13]分析的擺動活齒傳動系統結論一致。

分別取k1e、k2e和k3e的最大值、最小值及平均值,可以計算出扭轉振動系統最大固有頻率fmax、最小固有頻率fmin及平均固有頻率fmea,計算結果如表2所示。

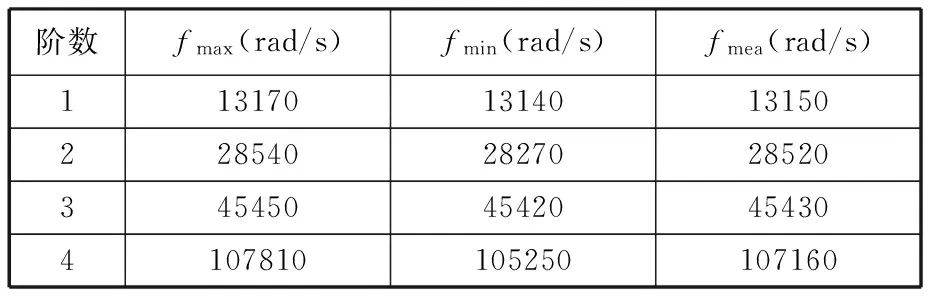
表2　扭轉振動系統固有圓頻率

綜合上述結論，可以提出兩種計算圓柱正弦活齒傳動扭轉振動固有頻率的方法：

(1)二階時變扭轉振動系統固有頻率可以轉化到一個周期內通過矩陣迭代攝動法求解系統的固有頻率，這將大幅度減小求解時變系統固有頻率精確值的計算量。

(2)扭轉振動系統剛度矩陣直接取平均值，則將圓柱正弦活齒二階時變扭轉振動系統轉化為二階常系數扭轉振動系統，這樣求出的系統扭轉振動固有頻率誤差很小，通過這種方法更加簡化了扭轉固有頻率的計算，而且也完全滿足工程實際要求。

5　結論

本文建立了一套完整求解圓柱正弦活齒傳動扭轉振動模型嚙合剛度的方法，并結合具體實例進行了分析說明,發現扭轉振動系統剛度矩陣具有周期性，求出了周期計算公式，指出了扭轉振動系統是一個時變系統，提出了該時變系統固有頻率的兩種簡化求解方法，一種方法是在剛度矩陣周期內利用矩陣迭代攝動法求解系統在不同位置時的固有頻率精確值，另一種方法是將扭轉剛度矩陣看作定值，將扭轉振動時變系統轉化為常系數線性系統，求解平均固有頻率，計算精度完全滿足工程要求。

[1]Li Guixian,Sun Yu,Zhang Xin.Meshing Theoretical Study and Simulation on Cylindrical Tri-sine Oscillating Tooth Gear Drive[J].Journal of Donghua University,2004,21(1):117-120.

[2]李瑰賢，孫瑜，李笑，等. 新型微型減速器傳動比及傳動條件的研究[J]. 機械傳動,2003,27(3)：12-13.

Li Guixian,Sun Yu,Li Xiao,et al.Transmission Ratio and Transmission Condition of New Type Mini-reducer[J].Journal of Mechanical Transmission,22003,27(3):12-13.

[3]李瑰賢,孫瑜,李笑,等.圓柱正弦活齒傳動受力分析研究[J].哈爾濱工業大學學報,2003,35(11):1381-1383.

Li Guixian,Sun Yu,Li Xiao,et al.Mechanics Model of Cylinder Sine Oscillating Tooth Gear Drive[J].Journal of Harbin Institute of Technology,2003,35(11)：1381-1383.

[4]孫瑜,李瑰賢,魏海軍.圓柱正弦活齒減速器模糊故障樹分析[J].大連海事大學學報,2004,30(3):77-80.

Sun Yu,Li Guixian,Wei Haijun.Fuzzy Fault Tree Analysis of Cylinder Sine Oscillating Tooth Reducer[J]. Journal of Dalian Maritime University,2004,30(3):77-88.

[5]李劍鋒,董新蕊.凸輪激波滾動活齒傳動嚙合力分析方法[J].機械工程學報,2008,44(5):39-44.

Li Jianfeng,Dong Xinrui.Method of Meshing Force Analysis for the Movable Rolling Teeth Transmission with Cam Actuating[J].Chinese Journal of Mechanical Engineering,2008,44(5):39-44.[6]鄒英永,溫建民,于廣濱.徑向力和彎矩聯合作用下滾子軸承的剛度計算[J].中國機械工程,2006,17(15):1572-1575.

Zou Yingyong,Wen Jianmin,Yu Guangbin.Stiffness Calculation of Roller Bearing with Radial Force and Moment Loads[J].China Mechanical Engineering,2006,17(15)：1572-1575.

[7]李偉建,潘存云,王榮吉. 空心圓柱滾子軸承剛度分析[J]. 中國機械工程,2009,20(7):795-798.

Li Weijian,Pan Cunyun,Wang Rongji.Stiffness Analysis of Hollow Cylindrical Roller Bearings[J].China Mechanical Engineering,2009,20(7):795-798.

[8]An Zijun,Gao Fei.Engagement Rigidity Analysis of Swing-Rod Movable Teeth Transmission[J].Machinery,2007,45(5)：3-5.

[9]傅則紹.微分幾何與齒輪嚙合原理[M].山東:石油大學出版社,1999.

[10]程光仁,施祖康,張超鵬.滾珠螺旋傳動設計基礎[M].北京:機械工業出版社,1987.

[11]An Zijun,Gao Fei. Torsion Vibration Analysis and Modeling Research on Swing-Rod Movable Teeth Transmission[J]. Machine Design and Research，2007，23(3):79-81.

[12]邵忍平. 機械系統動力學[M].北京：機械工業出版社,2005.

[13]Liang Shangming,Zhang Junfu，Xu Liju，et al. Dynamic Model of Swing Movable Teeth Transmission System Vibration[J]. Journal of Vibration Engineering，2003，16(3):31-35.

(編輯蘇衛國)

Study on Stiffness of Torsional Vibration System on Cylinder Sine Oscillation Tooth Transmission

Zhou SizhuZeng YunyunYuan Xinmei

Yangtze University,Jingzhou,Hubei,434000

In accordance with the force conditions of cylinder sine oscillation tooth transmission,a model of meshing force analysis under theoretical conditions was proposed based on the hypothesis of stretch small distortion and distortion congruity.According to Hertz theory and geometric relation of engagement pair,engagement stiffness models of the engagement pair were established,and the calculation formulas of the engagement stiffness and the principal curvature of the contact point were deduced.The torsional vibration model of cylinder sine oscillation tooth transmission were established by energy conservation principle,and the calculation formulas of equivalent torsional stiffness were given,forming a complete set of analysis and calculation methods of system stiffness matrix,and the presented methods was illustrated through an example.The fact is discovered,that the torsional vibration is a time-varying system and the system stiffness matrix shows the characteristics of cycle distribution,and the cycle calculation formula are found.Two simplified methods for solving natural frequency of the torsional vibration system were pointed out.The acquired results can be adopted as the analytical base for structure design and vibration analysis.

cylinder sine oscillation tooth transmission;meshing force；engagement stiffness;equivalent torsional stiffness;system stiffness matrix

2014-10-16

國家自然科學基金資助項目(51374041)

TH132.425DOI：10.3969/j.issn.1004-132X.2015.20.003

周思柱,男,1963年生。長江大學機械結構強度與振動研究所教授、博士研究生導師。主要研究方向為機械結構強度與振動。獲省級科技進步一等獎1項、二等獎4項、三等獎2項，中國石油與化工科技進步獎4項，中國機械工業科學技術二等獎1項。發表論文150余篇。曾運運,男,1988年生。長江大學機械結構強度與振動研究所碩士研究生。袁新梅,女,1979年生。長江大學機械工程學院博士研究生。