估計含水層參數的粒子群優化算法
袁帆


摘 要 以第一類越流系統情況下的非穩定井流問題的解析解為基礎,將抽水試驗數據用粒子群優化算法來分析,估計含水層參數。數值試驗結果表明:粒子群優化算法可以有效地應用于分析抽水試驗數據,確定含水層參數。具有運算速度快和計算精度高等優點。
關鍵詞 越流 粒子群優化算法 抽水試驗 含水層參數
中圖分類號:TV211.1 文獻標識碼:ADOI:10.16400/j.cnki.kjdkz.2015.10.021
Application of Particle Swarm Optimization to
Determination of Aquifer Parameters
YUAN Fan
(College of Science, Changan University, Xi'an, Shaanxi 710064)
Abstract Based on the analytical solutions to well flow problems of unsteady flows in the first type leakage system,the particle Swarm algorithm was employed to analyze the data of pumping tests to determine aquifer parameters.Numerical results show that the Particle Swarm algorithm can be effectively applied to analyzing the data of pumping test for estimation of aquifer parameters, this method has fast speed and high accuracy.
Key words leakage system; particle swarm algorithm; pumping tests; aquifer parameters
遺傳算法是對粒子進行選擇、交叉和變異處理,而粒子群優化算法(PSO)是將操作中的每一個個體視為N維搜索空間中的一個沒有體積和質量的微粒,每一個微粒代表一個被優化問題的解。在N維搜索空間中,粒子個數為,第個粒子的位置和速度分別為 = [,,…,], = [,,…,],則在第 + 1次迭代計算時,粒子根據以下規則來更新自己的速度和位置:
式中:(),( )為粒子在第次迭代時第維的位置和速度;為粒子達到目前最佳位置時第維的位置坐標;為種群目前達到最佳位置時第維的位置坐標;為慣性權重系數,一般從0.9線性遞減到0.4;、為加速因子;是[0,1]之間的隨機數。為了防止微粒遠離搜索空間,限制微粒飛行的最大速度被定義,其值通常取決策變量的上下界之差。
1 粒子群優化算法的構造
標準PSO算法步驟為:
Step1:隨機初始化粒子的位置和速度,將每個粒子的當前位置設為pbest,并計算出當前的個體極值和全局極值,并記錄全局極值的粒子序號,將其位置設為gbest;
Step2:初始化迭代次數和,若<且滿足防止早熟收斂所設置的迭代次數<時進入循環,否則輸出最優結果;
Step3:用粒子群優化算法更新每一粒子的速度和位置,評估粒子的適應度值,更新局部最優pbest和全局最優gbest;
Step4:迭代 = ?+ 1并返回Step2,直到精度達到要求時輸出結果。
2 汗土什公式
在含水層為均質、各向同性和無線延伸的理想條件下,以定流量進行抽水,在抽水開始后時刻,含水層中距抽水主井距離為點處的水位降深可以表示為:
式中:表示水頭降深值(m);表示抽水流量(m3/s);T表示含水層的導水系數(m2/s);為距抽水主井的距離(m);為越流補給因子(m-1);為越流井函數;表示含水層的儲水系數,為無量綱時間。其表達式為
在應用PSO算法時要求(5)式所要求的目標函數達到最小,即
式中:為在抽水開始后第時刻觀測到的實際水位降深值(m);為利用(3)式計算得到的第時刻的水位降深值(m);為待估參數向量,在第一類越流系統中有3個待估的含水層參數,分別是導水系數、儲水系數和越流補給因子1/B,分別視為,,。
3 數值試驗
3.1 算例
本文引用文獻[6]中給出的越流條件下實際抽水試驗數據進行數值試驗。表1中給出的是在抽水開始后距抽水主井距離為 = 12.19m處觀測孔中觀測到的實際水頭降深數據,試驗中的抽水流量為 = 17.0m3/min,持續抽水時間為420min。在應用PSO算法進行計算的過程中,只采用表1中的部分數據(本文中采用序號為奇數的觀測數據進行計算,序號為偶數的觀測值作為檢驗數)。
3.2 試驗結果的可靠性分析
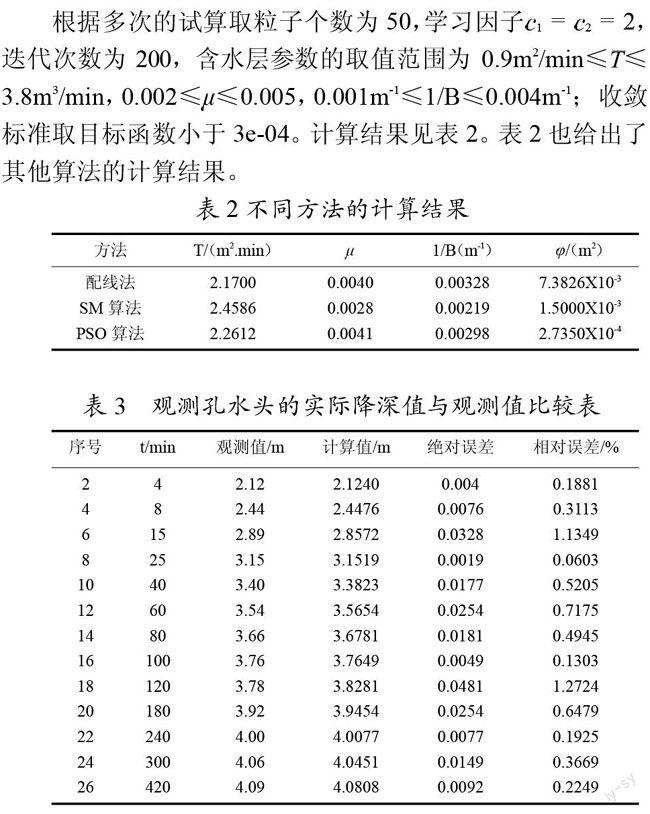
根據多次的試算取粒子個數為50,學習因子 = ?= 2,迭代次數為200,含水層參數的取值范圍為0.9m2/min≤≤ 3.8m3/min,0.002≤≤0.005,0.001m-1≤1/B≤0.004m-1; 收斂標準取目標函數小于3e-04。計算結果見表2。表2也給出了其他算法的計算結果。
根據表2的數據可以看出粒子群優化算法計算的數據和其他算法計算出的結果比較接近,較可靠,且目標函數值達到0.00047,計算精度明顯高于其他算法。且在50次試驗中的平均迭代次數為72,平均迭代時間為6.84s,說明粒子群優化算法迭代速度較快。
為了檢驗PSO算法反演含水層參數的可靠性,將表2中所求得的參數、、1/B代入公式(3),分別求出表1中未參與含水層參數反演運算的各時刻水頭降深值,并與實際觀測值進行比較,從表3中可以看出,用所求得的參數反演各個時刻水頭值與實際觀測值得誤差很小,絕對誤差最大不超過5%,相對誤差最大不超過1.5%,觀測值與實際值擬合良好,這說明PSO算法的計算結果是可靠的。
4 結語
粒子群優化算法具有全局尋優能力強的特點,利用解的適定性將反問題化為一系列的正問題進行求解,克服了實際測量數據的不穩定性對反問題解的精確性的影響。數值試驗表明:粒子群優化算法反演含水層參數具有比較好的精度,是一種值得在實際中推廣的反演含水層參數的方法。
參考文獻
[1] 李敏強,寇紀淞.遺傳算法的基本理論與應用[M].北京:科學出版社,2002.3.
[2] Kennedy J,Eberhart RC.Particle swarm optimization[C].In:IEEE International Conference on Neural Networks, Perth, Australia,1995:1942-1948.
[3] Eberhart R,Kennedy J.A new optimizer using particle swarm theory[C].In:Proc of the sixth international ?symposium on Machine and Human Science,Nagoya,Japan,1995:39-43.
[4] 范娜,云慶夏.粒子群優化算法及其應用[J].信息技術,2006(1):53-56.
[5] 陳崇希,林敏.地下水動力學[M].武漢:中國地質大學出版社,1999:70-120.
[6] U.S.Department of the Interior(USDI).Ground water manual[M].Washington,D.C:Bureau of Reclamation,1981:121-127.
[7] 張鵠志,郭建青.粒子群優化算法在確定越流含水層參數中的應用[J].水利水電科學進展,2011(3):13-16.

