西部獨立學院數學試卷命題初探
漢巍 李蕊彤
以某獨立院校大學一年級學生為研究對象,采用自編試卷、正規考試的方式進行調查,被試176人,對數學試卷命題問題進行研究。結果表明,該試題所體現的命題思路和命題方式可以在一定程度上反映出學生的學習水平,但在命題難易度和考察的重點方面出現了問題。本文針對上述結果進行了分析,并提出幾點建議。
一 問題的提出
獨立學院學生來源于“三本”,這就造成獨立學院的生源多數均比“一二本”要差,而且一般都差在數學與英語上,這就給獨立學院的數學教學帶來極大的問題。教學中的問題很多,本文主要聚焦在試卷試題的安排上。獨立學院的大部分教學方法,教學制度等諸多方面均學“一二本”學校,同樣的試卷模式、命題思想也均來源于“一二本”學校,試卷難易度僅人為的略作降低,但對于如此改動是否符合獨立學院的實際,是否符合學生對相關知識的認識,本文試圖通過一些調查研究,做出一些討論,為獨立學院數學教學提出一些有益的建議。
二 對象與方法
(一)對象
本次調查對象選自于甘肅省蘭州市某獨立學院大學一年級176名學生。甘肅省蘭州市屬于典型的西部地區,學生大部分來自于西北五省,極少數的學生來自四川、山東等省份,故選擇此校學生具有代表性。另外,本研究主要選擇大學一年級第一學期的學生為被試對象,是因為大學數學課程開設在大學一年級與大學二年級第一學期,而入學一年級學生剛經歷完高考,對于學習尚存一定的熱情與勁頭,對待考試比較認真,可以比較好地反映出試卷對于學生的難易度,而大二的學生對待考試已有懈怠之心,所以選擇大一學生是比較有代表性的。
(二)方法
由于此類研究尚無現成方案,故本次以一次試卷的結果進行分析,本試題以該院歷年考題為藍本,采用相同的出題思路和出題難度。本試題共有五道大題——選擇、填空、計算、應用、證明、選擇、填空題均共有5道小題,計算題共有7道小題,應用題共有2道小題,證明題有1道。每道題均可得到相應的難度系數,一道題難度系數越高說明對于學生而言這道題的難度越低,反之,一道題的難度系數越低說明對于學生而言這道題的難度越高。此次試卷的考察形式為正規考試形式,為了使學生重視此次考察,將此次考察成績與學生最終成績相關,且此次考察是在學生將本學期課程內容學完后進行的,故此次考察可視為學生的一次真實水平的體現。考試結束后將學生答題結果錄入電腦,用EXCEL系統進行分析。
三 結果
(一)客觀題結果
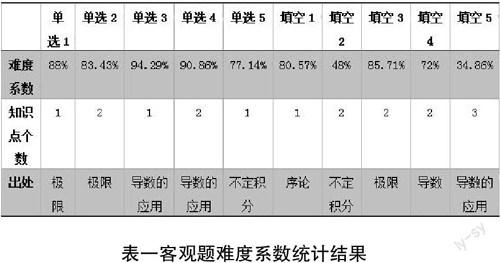
表一說明了學生客觀題的得分情況,其中選擇題的難度系數最低的是第五題,此題考察的知識點來源于不定積分部分,涉及知識點1個。難度系數最高的是第三題,此題考察的知識點來源于導數的應用部分,涉及知識點1個。其中填空題的難度系數最低的是第五題,此題考察的知識點來源于導數的應用部分,涉及知識點3個。難度系數最高的是第三題,此題考察的知識點來源于極限部分,涉及知識點2個。
(二)計算題結果
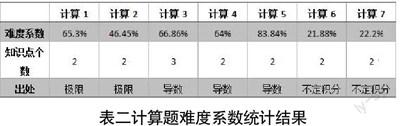
表二說明了學生計算題的得分情況,其中選擇題的難度系數最低的是第六、七題,此題考察的知識點來源于不定積分部分,涉及知識點2個。難度系數最高的是第五題,此題考察的知識點來源于導數部分,涉及知識點2個。
(三)應用、證明題結果
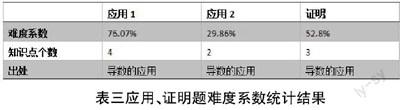
表三說明了學生應用、證明題的得分情況,其中難度系數最低的是應用第二題,此題考察的知識點來源于導數的應用部分,涉及知識點2個。難度系數最高的是應用第一題,此題考察的知識點來源于導數的應用部分,涉及知識點4個。
四 分析與結論
就一張試卷而言,難度系數在70%以上的試題應視為易題,40%~70%之間的試題應視為中檔題,40%以下的試題應視為難題,且易題、中檔題、難題的比例應為3:5:2,各種題型中易、中、難題目的比例分別為選擇題3:2:1、填空題2:1:1,而解答題一般不安排易題,中檔題和難題的比例為1:1。縱觀三張表格可見其中易題所占分數比例為39%,中檔題比例為36%,難題比例為25%。對比相關原則可以發現此張試卷所出現的問題為中檔題偏少,這反映了教師對學生水平的估計稍有差距,認為學生學習水平較低,才會出現易題較多的情況。雖然此試卷中難題的比例達到25%,但值得注意的是此試卷中學生難度系數低于40%的題目中真正涉及到多個知識點的僅有填空題5一個,而學生難度系數最低的兩個題目均出自于不定積分部分,同時可見凡試題涉及到不定積分部分時,難度系數均低于相關題目類型的平均水平。這就說明,一方面,原本在教師看來難易度較低的不定積分的題目(涉及知識點僅有1到2個)成為了難題,如刨去不定積分的題目,難題的比例將大大下降,甚至可以說本套試卷中基本無難題。這再一次說明教師對于學生的學習水平估計偏低。另一方面,不作為難題的不定積分題目成為了難題,說明學生對不定積分的掌握遠非教師考慮的那樣樂觀,這當然是教學中出現的問題,清晰地反映在試卷的難度系數上。相同的情況也在同為難度系數較低的應用題2上發生了,此題涉及的知識點僅有兩個,計算也較為簡單,但難度系數僅為29.86%。究其原因,此題涉及到的知識為導數在經濟上的應用,而此部分知識在教學中并未作為重點,導致學生也未引起足夠的重視,以至難度系數較低。綜合對于難題的分析可見,命題者僅重視考察學生掌握知識的全面性,但對學生知識掌握程度考慮不足。
五 對試卷命題的若干建議
(一)命題態度
首先,由于大學階段的最終成績普遍由平時成績與期末考試兩部分構成,這就使得期末考試不再像中小學階段那樣具有絕對的決定性作用,因此在大學考試命題中,出現了兩種思路。其一,既然有平時成績作底,那么期末考試題目可以稍微難一些,以便體現命題者的水平,顯示教師教學水平的高度,這樣的結果往往是試卷卷面成績偏低,及格率全靠平時成績來拉升,造成平時成績虛高,無法真正體現學生平時的表現,進一步造成學生為了提高成績,只重視考前的突擊及作弊。其二,既然要和平時成績結合,那么期末考試就可以稍微容易一些,用不著為難學生,本次的試卷就有此種傾向,這樣的結果往往是卷面上大部分學生可以輕易及格,學生成績區分度不大,認真學習的學生與考前突擊的學生成績差距較小,造成學生學習懈怠情緒的產生,無法真正體現教學水平,反映教學質量。因此,命題者應嚴肅面對期末考試的出題工作,重視期末考試,按照命題規律出題,難易適中,不追求過難或過易,使成績反映教學和學習水平。
其次,命題者應正確看待獨立學院學生的數學學習水平。獨立學院的學生距“一二本”院校的學生是有一定差距,但在大學數學課程的學習中,兩者近乎站在相同的起點上,兩者的差距并沒有想象中的那么大。命題時適當安排部分難題,以便拉開成績檔次,增加區分度,更有利于全面了解、掌握學生的學習情況。
(二)命題方式
命題者應以教學重點為導向,教學中出現的重難點應作為命題重點,以考試為抓手促進學生學習。考察需要全面,但非面面俱到,應切實避免出現中檔題變難、難題更難的情況,教學難點可以分為考察基本概念基本計算的中檔題,與考察學生學習能力的難題的兩個不同試題出現。
研究獨立學院數學試卷命題的相關問題,有利于衡量獨立學院的數學水平,可以避免由于命題失誤造成的評價失真,對教與學都有較大的意義。由于作者水平有限,對現有研究成果掌握不足,僅對獨立學院數學試卷命題做出了很有限的研究,希望本文可以引起大家對獨立學院數學試卷命題的重視,促進教學的發展和進步。
參考文獻
[1]趙樹嫄.經濟應用數學基礎(一):微積分[M].北京:人民
大學出版社,2012.
[2]華東師范大學數學系.數學分析上冊[M].北京:高等教
育出版社,1991.
[3]龔德恩.經濟數學基礎(第一分冊:微積分)[M].成都:四
川人民出版社,2005.

