電力系統擴展黑啟動方案動態綜合評估

顧雪平 王大江 梁海平 劉 艷

（華北電力大學新能源電力系統國家重點實驗室 保定 071003）

1 引言

智能電網是世界電力工業的共同發展趨勢[1]，建設智能電網將使未來電網更加安全可靠，但其安全穩定運行仍然受到外部環境因素和內部技術問題的影響，災難性事故仍無法完全避免，世界范圍內影響人口最多的印度2012年“7.30”、“7.31”大停電事故再次敲響了警鐘[2]。科學合理的恢復方案是應對大停電事故的有效預案，對事故后的有序恢復起到重要作用，擴展黑啟動策略的提出為恢復控制提供了一種新思路[3]，相比于起動一臺機組的常規黑啟動方式，擴展黑啟動策略能夠為后續恢復提供更多功率，加快恢復進程，因此，對擴展黑啟動方案評估優選具有重要意義。

黑啟動方案評估排序是黑啟動問題研究的重要內容之一，眾多專家學者將多種評估決策理論引入到該研究中，作出了大量有益的探索，取得了一些卓有成效的成果，主要的評估方法包括數據包絡分析模型及與其他方法相結合的改進模型[4-6]、模糊評估方法[7-11]、群體決策理論[12-14]、熵權決策方法[15]、Vague集理論[16]、主成分分析法[17]幾類，但現有研究多數停留在靜態評估層面，只利用黑啟動階段的評價值進行方案評估排序，未將方案對后續恢復的影響納入到評估結果中，而大停電后的恢復過程是一個連續的動態過程，黑啟動階段是恢復的初始階段，所形成的局部網絡是后續恢復的基礎，不同的方案對后續恢復影響不同，方案的評價不僅要看黑啟動階段的恢復狀況，還要考慮對后續恢復過程的影響而進行綜合評估，選擇在黑啟動階段和后續恢復階段整體上最優的方案。

本文在對現有黑啟動方案評估及動態綜合評估理論學習借鑒的基礎上[18-21]，以時序動態視角對擴展黑啟動方案進行動態綜合評估。首先提出了動態評估的框架，將時間維度劃分為黑啟動階段和后續恢復階段兩個時段，構建了兩個時段的評估指標，采用組合賦權法得到指標的綜合權重，以線性加權模型對各時段指標集結得到待評估方案不同時段的評價值。在此基礎上，求解基于“時間度”概念的非線性熵值規劃法確定黑啟動階段和后續恢復階段的最優時間權重，以時序加權平均算子和時序幾何平均算子組成的混合算子模型對兩時段評價值再次集結，得到方案所有時段的最終綜合評估結果。

2 擴展黑啟動方案動態綜合評估框架及指標體系

2.1 方案動態綜合評估框架

靜態評估主要用于解決由指標集、方案集構成的二維空間決策問題，動態評估是在二維決策空間的基礎上還要考慮時間維度的三維空間決策問題，評估數據由平面數據演變為具有時間標度的時序立體數據。本文嘗試從方案集、指標集、時間集三個維度對擴展黑啟動方案進行動態綜合評估。為使其綜合評估結果包含黑啟動階段的恢復結果和對后續恢復的影響，本文借鑒現有系統恢復研究中將恢復過程分階段考慮的方式，將恢復過程時間維度劃分為黑啟動恢復階段、后續恢復階段兩個時段，即從當前和將來發展趨勢兩部分進行動態綜合評估，使評估結果更全面科學，評估框架如圖1所示。對擴展黑啟動方案實施動態綜合評估，決策者既能從宏觀整體上掌握方案的總體評估結果，又能了解到恢復過程中不同階段的動態恢復狀況，為綜合決策提供多角度的參考依據。由于主網架建立后的全面負荷恢復階段目標較單一，本文的后續恢復指后續的網架重構，對于后續網架重構，以待評估方案在黑啟動階段形成的局部網絡為基礎，采用文獻[22]提出的“分時步、整體尋優”策略，即從網架重構整體最優的角度優化出每一時步恢復的機組和負荷進而完成后續恢復。

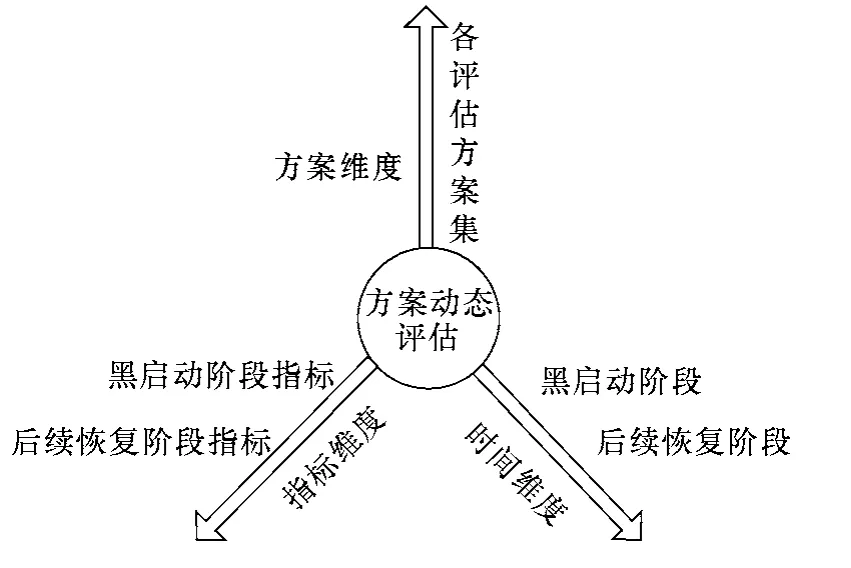
圖1 擴展黑啟動方案動態評估框架Fig.1 Dynamic assessment framework of extend-black schmes

2.2 評估指標體系

評估指標從不同方面反映了系統恢復各階段的多種因素，遵循指標制定的科學性、系統性、實用性等基本準則，結合系統恢復的具體實際，參考已有研究成果，從黑啟動階段和后續恢復階段兩個時段實際特點分別提煉各自的指標，構建適用于擴展黑啟動方案動態評估的指標體系，見表1。

表1 評估指標體系Tab.1 The assessment index system

表1中部分指標定義如下：

（1）路徑指標I1反映了黑啟動階段被啟動機組恢復路徑的狀況，將路徑指標I1定義為

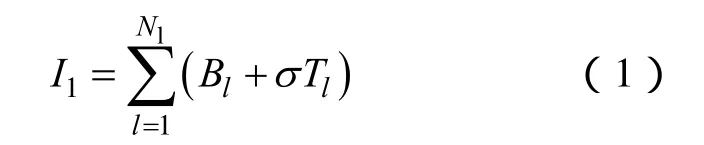
式中，Nl為黑啟動階段恢復的線路數；Bl為線路l折算到同一電壓等級下的電納；Tl為線路l是否經過電壓等級變換，是為1，否為0；σ為轉換系數。

（2）技術指標I4包括充電路徑過電壓、黑啟動電源自勵磁、電壓穩定和頻率穩定四個單項校驗指標，各單項指標計算準則見文獻[4]，其中電壓穩定與頻率穩定指標分別取啟動的多臺機組中電壓下降最大、頻率跌落最大值為本方案指標值。以所有待評估方案中各單項指標最優值為基準進行歸一化，由歸一化后的各單項指標疊加組成技術指標I4。

（3）黑啟動階段啟動的機組不僅是黑啟動階段恢復效果的體現，也影響后續恢復，綜合考慮機組性能、位置重要度因素，將機組恢復指標I5定義為

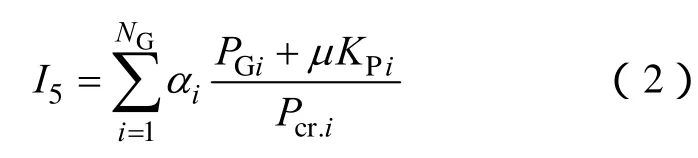
式中，NG為恢復的小系統中機組個數；αi為機組i所在節點的重要度，以節點收縮后的網絡凝聚度表示[23]；PGi為機組i的額定功率；KPi為機組i的爬坡速率；cr.iP為機組i的啟動功率；μ為轉換系數。

（4）啟動功率指標I7反映了后續恢復對啟動功率的需求，以后續恢復各時步需要的啟動功率加權和表示為

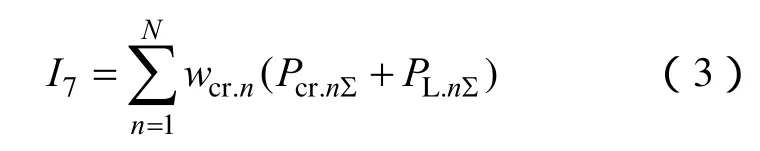
式中，N為后續恢復時步總數；Pcr.nΣ為第n時步恢復的機組啟動功率之和；PL.nΣ為n時步恢復的負荷總量；wcr.n為n時步啟動功率的權值。

（5）路徑指標I8反映了后續恢復階段機組和負荷恢復的恢復路徑狀況，計算公式為

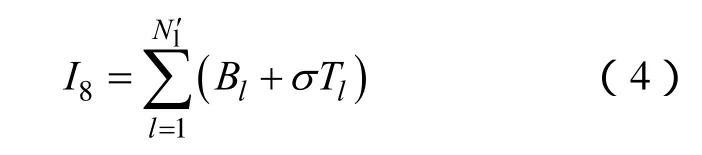
式中，N'l為后續恢復階段恢復的線路數。

（6）定義恢復機組容量指標表征后續恢復階段機組的恢復效果，以后續恢復各時步恢復的機組容量加權和表示。即

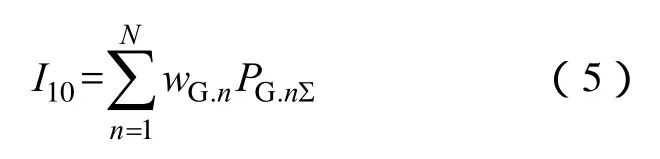
式中，wG.n為n時步啟動的機組容量權值；PG.nΣ為n時步恢復的機組額定容量和。

（7）恢復負荷量指標I11體現了后續恢復中負荷恢復的成果，以各時步恢復的負荷量加權和表示，即

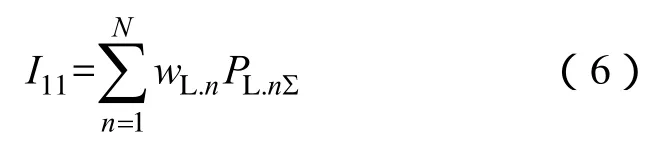
式中，wL.n為時步n恢復負荷的權值；PL.nΣ為時步n恢復的負荷量。

（8）定義骨架網絡度指標衡量最終形成的網架結構重要性，從復雜網絡拓撲特性角度研究最終形成的目標網架骨架網絡度，將其定義為

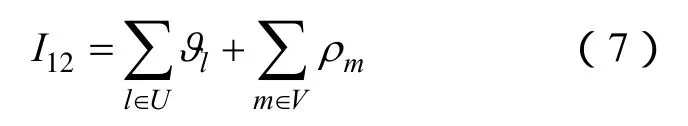
式中，U為最終恢復的目標網架所有線路集合；l?為線路l的重要度，以其介數表示[23]；V為最終恢復的目標網架所有節點集合；mρ為節點m的重要度。

3 基于線性加權模型的方案各時段靜態評估

3.1 指標標準化處理

將恢復過程時間集表示為ψ=｛t1,t2｝（t1表示黑啟動階段，t2表示后續恢復階段），待評估的方案集為S=｛s1,s2,…,sn｝ ，不 同 時 段 的 指 標 集 為I(tk)=｛I1(tk),I2(tk),…,Im(tk)｝（k=1,2），方案si(i=1,…,n)在tk時段的第j(j=1,…,m)個指標值為(tk)，由S中所有方案不同時段全部指標(tk)｝構成的時序立體數據表表示為(tk)｝，(tk)｝中各指標量綱不完全相同，不便于分析比較，影響到評價結果的合理性，為使指標數據間具有可比性，需進行標準化處理。本文采用極差化標準化方法，該方法對原始指標數據的數量及分布無要求，采用線性化方法對原始指標數據標準化處理，標準化后的指標數據與原始指標數據保持較高一致性，利于下一步評估，具體標準化步驟如下。

收益型指標標準化公式為

成本型指標標準化公式為

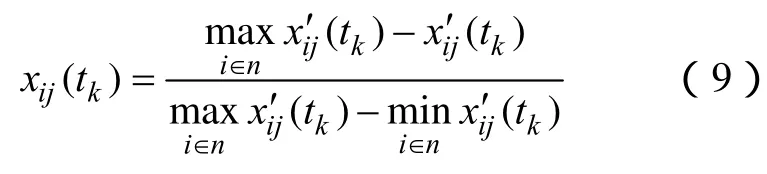
不同量綱的指標經過標準化處理后轉化為無量綱的標準化指標，xij(tk)∈[0,1]，消除了量綱的影響。

3.2 方案不同時段的靜態評估模型

在得到各方案標準化后的指標值組成的時序立體數據表｛xij(tk)｝后，通過線性加權模型對待評估方案si在tk時段所有指標集結得到該時段的評價值yi(tk)，集結模型為

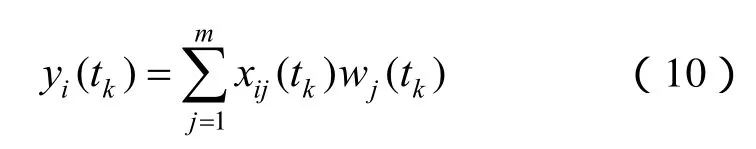
式中，wj(tk)為第tk時段指標j的綜合權重。

3.3 指標綜合權重的計算

本文采用組合賦權法計算指標的綜合權重，以專家賦權法確定不同時段指標的主觀權重，拉開檔次法計算指標的客觀權重[19]，兩者相結合得到指標綜合權重。

以專家賦權法確定不同時段各指標的主觀權重時，由于事實的不確定性和模糊性及專家知識結構和專業的差別等因素的影響，采用模糊語言權重更適合，模糊數則為刻畫語言模糊程度提供了有效工具，引入三角模糊數表示模糊權重，能夠有效地將模糊權重轉化為確定數值，模糊權重與相應三角模糊數如表2所示。

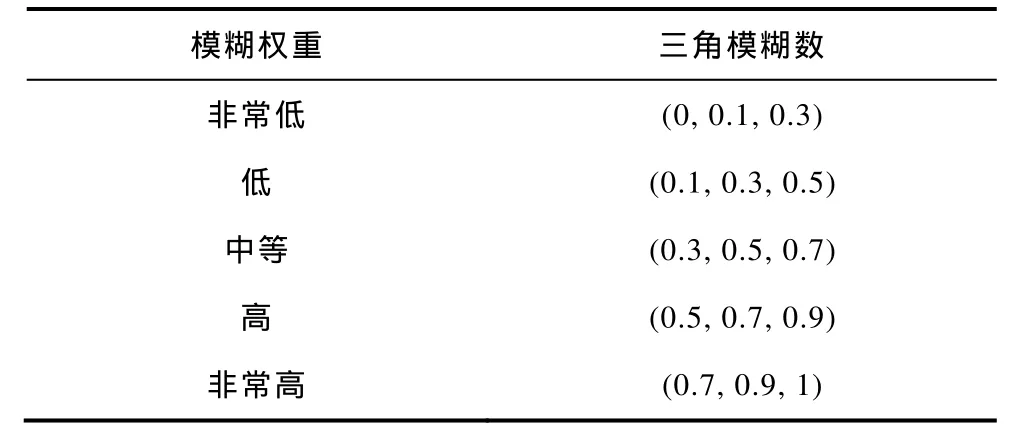
表2 模糊權重與相應三角模糊數Tab.2 Fuzzy weight and the corresponding triangular fuzzy numbers

設有L(L≥ 1)位專家對不同時段的指標進行賦權決策，第g位專家給出的tk時段第j個指標的模糊權重為，則綜合各專家決策信息的模糊權重為

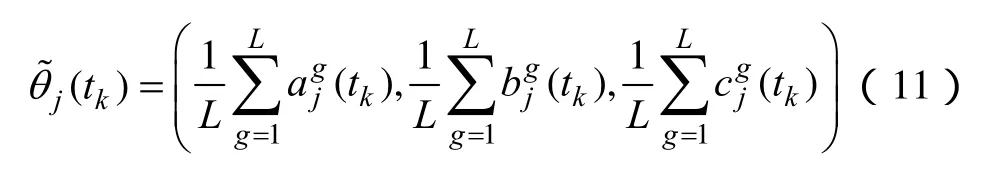
將指標的模糊權重明晰化處理，轉化公式為

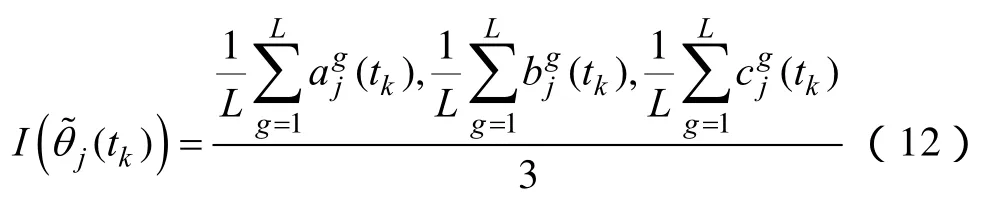
則tk時段指標j歸一化后的主觀權重為

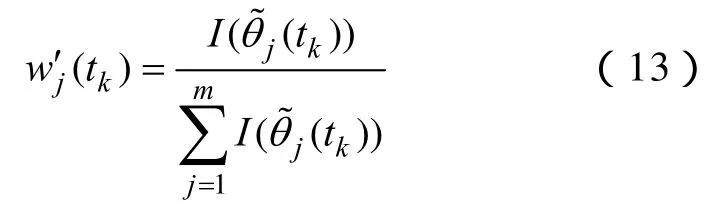
由式（11）～式（13）即可求出tk時段包含所有指標的主觀權重向量W'(tk)。

各指標的客觀權重采用盡可能體現出方案間差異的拉開檔次法確定，對于tk時段，由各待評估方案在此階段的所有指標組成的矩陣為，即時序立體數據表｛xij(tk)｝在tk時段的取值，設，求取Htk的最大特征值λmax()及相對應的特征向量，歸一化后的特征向量即為tk時段指標的客觀權重向量則tk時段指標j的綜合權重wj(tk)可由主觀權重和客觀權重得到，即

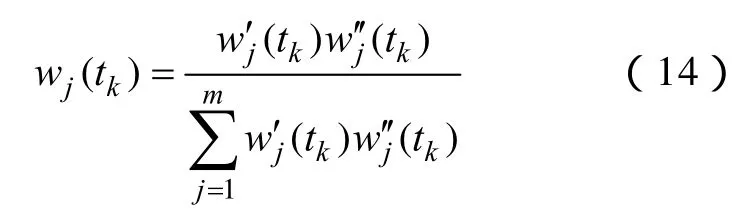
4 方案動態綜合評估

方案動態評估結果是黑啟動階段和后續恢復階段評價值的綜合體現，在求得方案si在黑啟動階段和后續恢復階段各自靜態評價值的基礎上，通過對兩個時段評價值在時間維上再次集結得到所有時段的動態綜合評價值，本文引入時序加權平均（Time Ordered Weighted Averaging Operator，TOWA）算子和時序幾何平均（Time Ordered Weighted Geometric Averaging Operator，TOWGA）算子組成的混合算子模型進行集結。

4.1 TOWA-TOWGA動態綜合評估模型

時序加權平均（TOWA）算子和時序幾何平均（TOWGA）算子是誘導有序信息集結算子簇中用于時序信息集結的算子，以下是兩種算子的定義[19]。

定義1 令T=｛1,2,…,t｝ ，稱為由二維數組構成的TOWA對，ui為時間誘導分量，ai為數據分量，時序加權平均(TOWA)算子定義為

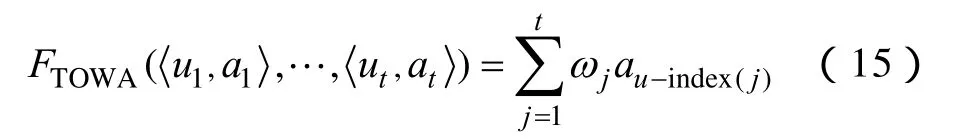
式中，ω=(ω1,ω2,…,ωt)T是與FTOWA相關的加權向量，ωj∈［0,1］，是按ui時間先后排列的第j個TOWA對數據分量，稱FTOWA是t維TOWA算子。

定義2 令T=｛1,2,…,t｝ ，稱為由二維數組構成的TOWGA對，ui為時間誘導分量，ai為數據分量，時序幾何平均(TOWGA)算子定義為

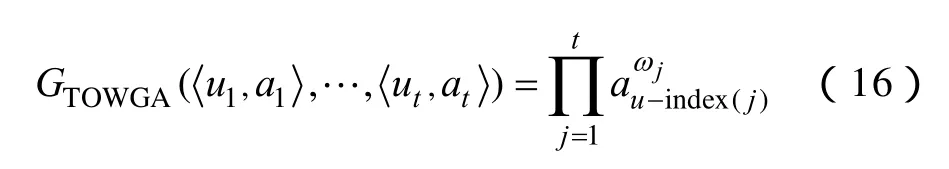
式中，ω=(ω1,ω2,…,ωt)T是與GTOWGA相關的加權向量，ωj∈［0,1］ ，是按ui時間先后排列的第j個TOWGA對數據分量，則稱GTOWGA是t維TOWGA算子。

由式（15）和式（16）可知兩種算子的實質是將時間誘導分量ui按時間順序排序后所對應的數據分量進行加權集結，但在數據集結過程中側重點不同，TOWA算子對時序數據線性加權，是“和性”的，突出了較大評價值的作用，TOWGA算子采用乘法合成法對時序數據集結，是“積性”的，突出了不同時段評價值的均衡性，因此，將兩種算子組合使用，能夠兼顧兩種算子的特點，結果將更為合理[20]。

在由方案si黑啟動階段評價值和后續恢復階段評價值分別構成的算子對及不同時段權重wtk的基礎上，對兩個時段評價值再次集結時，本文采用以下由TOWA算子和TOWGA算子組成的混合算子模型進行集結，即

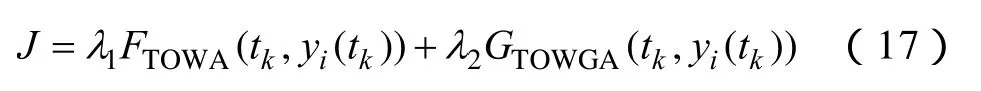
式中，λ1、λ2為比例因子，λ1≥0，λ2≥0，且λ1+λ2=1，分別表示TOWA算子和TOWGA算子在混合模型中所占的比重。

4.2 不同時段時間權重的確定

在以 TOWA-TOWGA混合算子模型對方案si黑啟動階段和后續恢復階段兩個時段的評價值再次集結時，時間權重wtk的確定極為關鍵，直接關系到綜合評價結果的合理性。本文以非線性熵值規劃法[19]求解各時段的時間權重，在求解權重前先給出時間度λ和權重向量熵I的定義。

定義3 由各時段時間權重wtk和總時段數K，時間權重向量熵I定義為

定義4 時間度λ定義為

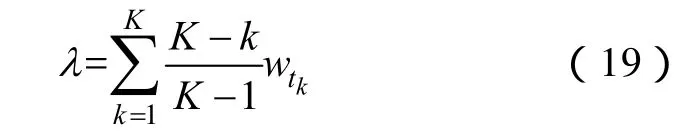
時間權重向量熵I反映了集結過程中時間權重包含信息的程度。時間度λ體現了集結過程中決策者對不同時段的重視程度。λ∈［ 0,1］，λ取值越接近0，表明越注重后續恢復階段評價值；取值越接近1，則越重視黑啟動階段評價值，λ取值標度見表3。

表3 時間度標度取值Tab.3 The value of time degree

非線性熵值規劃法求解各時段的時間權重wtk的準則是在事先確定時間度λ的前提下，即在體現決策者時序決策偏好下，盡可能地挖掘待評估方案的信息和時序上的差異信息來尋求最優的時間權向量，使主觀決策信息與客觀評價數據得到有效的融合，權重更為準確，可用如下的優化模型表示

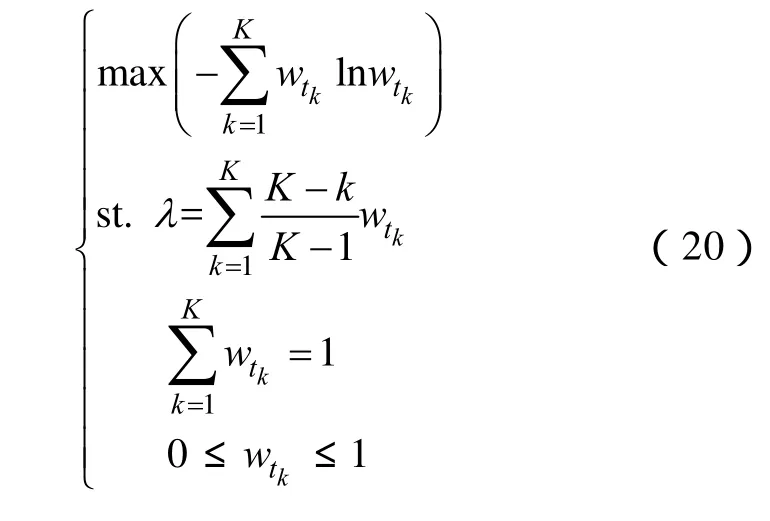
通過求解此非線性規劃模型即可得到黑啟動階段和后續恢復階段的最優時間權重wt1和wt2。

4.3 動態綜合評估流程

綜上所述，擴展黑啟動方案動態綜合評估的具體步驟如下：

（1）分別建立黑啟動階段和后續恢復階段的評估指標，構建評估指標體系，確定待評估方案集S。

（2）對S中每一方案si，在黑啟動階段恢復形成的小系統基礎上完成后續恢復，計算各方案不同時段的指標值，組成時序立體數據表，并標準化處理。

（4）由線性加權模型對方案si不同時段分別實施靜態評估，得到黑啟動階段評價值yi(t1)和后續恢復階段評價值yi(t2)。

（5）在給定時間度λ值的前提下，由非線性熵值規劃法求解得到黑啟動階段和后續恢復階段的各自時間權重wt1和wt2。

（6）由不同時段時間權重和TOWA-TOWGA混合算子模型對方案si兩個時段的評價值再次集結，得到最終的動態綜合評價結果。

5 算例分析

5.1 算例描述

采用本文提出的動態評估方法對圖2所示的新英格蘭10機39節點系統中擴展黑啟動方案實施評估，技術校驗合格的 3個擴展黑啟動方案見表 4，各臺被啟動機組參數見表5，PG為機組額定功率；Pcr為機組啟動功率；Kp為機組升負荷率；Tk為機組啟動時間；根據相加的兩項的相對重要性，轉換系數σ取0.5，μ取1。黑啟動階段采取零起升壓方式對恢復路徑充電，設充電時間為0.25h。

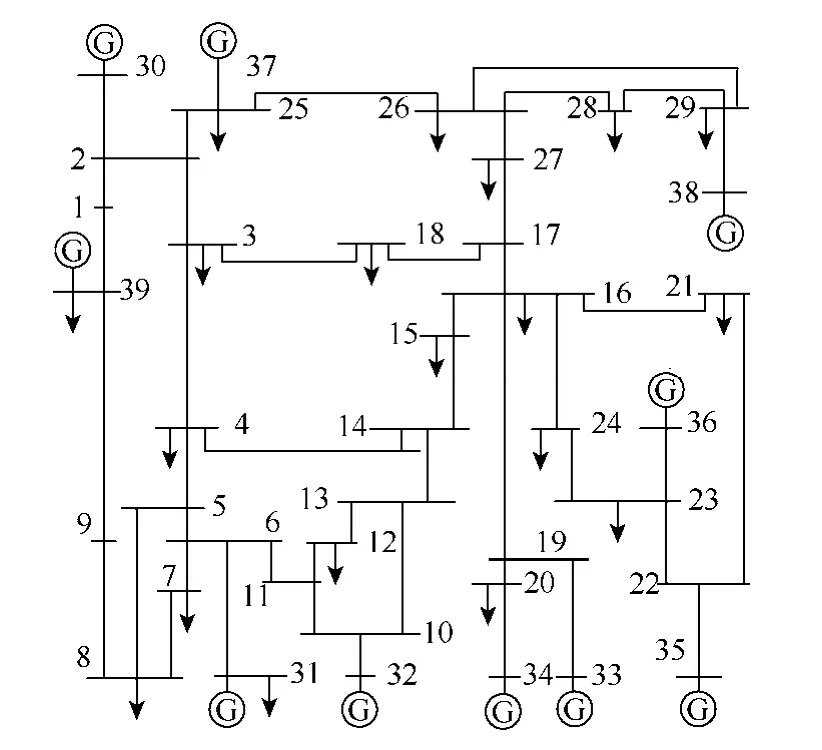
圖2 新英格蘭10機39節點系統Fig.2 New England 10-unit 39-bus power system

表4 技術可行的擴展黑啟動方案Tab.4 Technically feasible extended black-start schemes

表5 被起動機組的參數Tab.5 Parameters of the units to be restored

5.2 計算結果

利用文獻[22]提出的“分時步、整體尋優”重構策略在上述不同擴展黑啟動方案形成的局部網絡基礎上完成后續恢復，方案1和方案2一個時步完成后續恢復，方案3兩個時步完成后續恢復。由于后續恢復前期時步的啟動功率、恢復的機組、負荷相對后期時步更重要，權重系數wcr.n、wG.n和wL.n第一時步取1，第二時步取0.6。由機組及系統參數通過 BPA等仿真程序計算得到各待評估方案不同時段的指標值，組成的時序立體數據見表6。

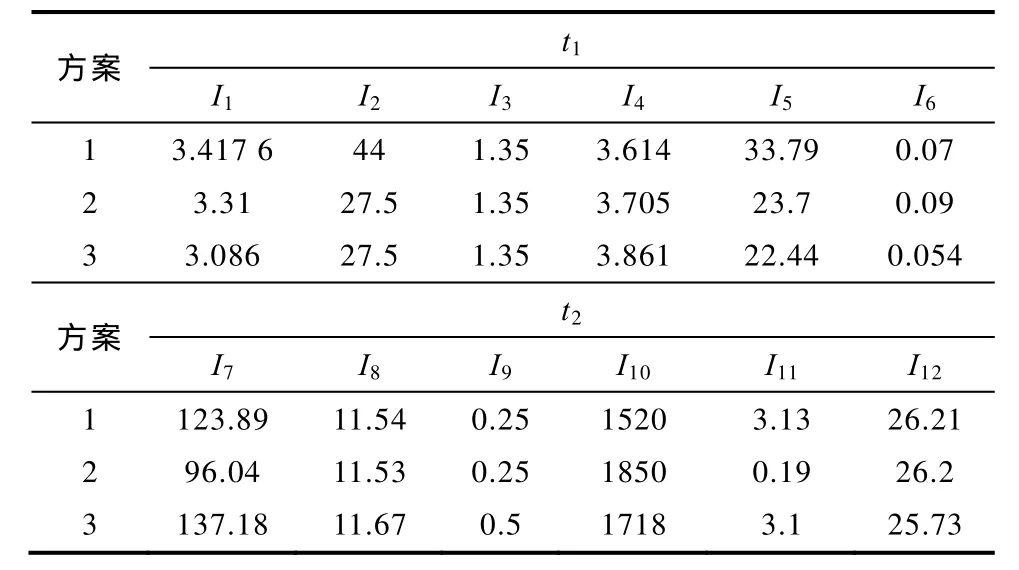
表6 評估方案時序立體數據表Tab.6 Timing order cubic data table of plans

通過3位專家對黑啟動階段和后續恢復階段指標賦權決策，由式（11）～式（13）得到兩個時段的主觀權重向量分別為

對時序立體數據表6中各指標值經過式（8）和式（9）標準化處理后，由拉開檔次法可得到兩個時段指標的客觀權重向量為

主客觀權重由式（14）相結合得到各時段指標綜合權重向量為

以線性加權模型（見式（10））對各方案不同時段分別進行靜態評估，得到各時段的評價值，見表7。

表7 各方案不同時段評價值Tab.7 Assessment value of different period for plans

在時間度λ取0.5，即同樣重視黑啟動階段和后續恢復階段，兩個時段的評價值同等重要，比例因子λ1、λ2均取0.5，表示兩種算子在混合算子模型中比重均衡。求解非線性規劃模型（見式（20））得到相應的時間權重向量為=(0.5,0.5)。

最后對待評估方案在黑啟動階段和后續恢復階段的評價值由式（17）再次集結，得到各方案的動態綜合評估結果，見表 8。以文獻[17]中采用的主成分分析法計算得到各方案的評估結果也列于表8中。

表8 各方案評價值Tab.8 Assessment value of plans

將傳統的逼近理想解法 TOPSIS應用于各方案不同時段的評估，由層次分析法得到的兩個時段的權重為

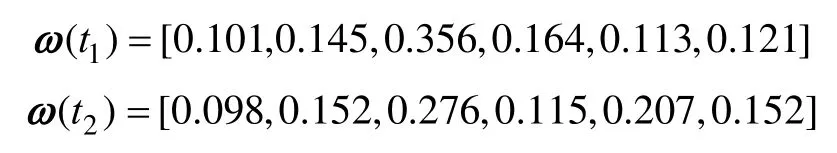
各待評估方案在兩個不同時段的評估結果見表9。

表9 各方案不同時段評估結果Tab.9 Assessment results of different period for plans

5.3 結果分析

由于各方案恢復的機組及形成的局部小網絡不同，由表6可知各方案在黑啟動階段的指標值不完全相同，因此在表7中各方案黑啟動階段的評價值不同，在黑啟動階段方案3評價值最大；由表6可知以不同方案形成的局部網絡為基礎的后續恢復過程也存在差異，方案1后續恢復評價值最大。由表7可知，黑啟動階段恢復效果好的方案在其后續恢復效果未必好。若僅以黑啟動階段的評價值作為優選方案的依據，則方案3為最優，但其后續恢復的效果不夠理想，在考慮對后續恢復影響的動態綜合評估中，方案2為整體上最優的方案，因此將方案對后續恢復的影響納入到方案動態綜合評估中是必要的。

由表8和表9可知，本文方法對各方案兩個時段的評估結果與傳統 TOPSIS法結果一致，動態綜合評估結果與文獻[17]主成分分析法評價結果一致，但 TOPSIS法得到的是各方案不同時段的評估結果，而主成分分析法的計算結果只能反映方案的整體評價結果，無法反映方案在黑啟動階段的恢復效果和對后續恢復的影響，也忽略了決策者的決策偏好。動態綜合評估既能從整體上對方案進行評估，又體現了方案不同階段的動態恢復水平，融入決策者的決策信息后，評價結果更全面。

6 結論

本文提出了一種基于時序動態理論的擴展黑啟動方案動態綜合評估方法。構建了反映黑啟動階段和后續恢復階段恢復特征的指標體系，主客觀相結合的組合賦權法使指標權重更加合理，采用線性加權模型對各時段內指標集結得到不同時段的評價值。非線性熵值規劃法能夠有效根據決策者的時序偏好求取各時段的最優時間權重，以時序加權平均算子和時序幾何平均算子組成的混合算子模型對兩個時段的評價值再次集結，克服了目前黑啟動方案評估中未考慮對后續恢復影響的不足。算例分析驗證了所提出方法的有效性，可為擴展黑啟動方案的決策提供科學依據，對大停電后的快速恢復起到重要作用。

[1] 張東霞,姚良忠,馬文媛. 中外智能電網發展戰略[J]. 中國電機工程學報,2013,33(31): 1-14.

Zhang Dongxia,Yao Liangzhong,Ma Wenyuan.Development strategies of smart grid in China and abroad[J]. Proceedings of the CSEE,2013,33(31):1-14.

[2] 湯涌,卜廣全,易俊. 印度“7. 30”、“7. 31”大停電事故分析及啟示[J]. 中國電機工程學報,2012,32(25): 167-174.

Tang Yong,Bu Guangquan,Yi Jun. Analysis and lessons of the blackout in Indian power grid on July 30 and 31,2012[J]. Proceedings of the CSEE,2012,32(25): 167-174.

[3] 顧雪平,鐘慧榮,賈京華,等. 電力系統擴展黑啟動方案的研究[J]. 中國電機工程學報,2011,31(28):25-32.

Gu Xueping,Zhong Huirong,Jia Jinghua,et al.Extended black-start schemes of power systems[J].Proceedings of the CSEE,2011,31(28): 25-32.

[4] 劉艷,顧雪平,張丹. 基于數據包絡分析模型的電力系統黑啟動方案相對有效性評估[J]. 中國電機工程學報,2006,26(5): 32-37.

Liu Yan,Gu Xueping,Zhang Dan. Data envelopment analysis based relative effectiveness assessment of power system black-start plans[J]. Proceedings of the CSEE,2006,26(5): 32-37.

[5] 林濟鏗,蔣越梅,岳順民,等. 基于DEA/AHP模型的電力系統黑啟動有效方案評估[J]. 電力系統自動化,2007,31(15): 65-70.

Lin Jikeng,Jiang Yuemei,Yue Shunmin,et al.Assessment of effective schemes for power system blackstart based on DEA/AHP[J]. Automation of Electric Power Systems,2007,31(15): 65-70.

[6] 吳燁,房鑫炎,張焰,等. 電網黑啟動的廣義模式評估算法[J]. 電工技術學報,2011,26(3): 155-161.

Wu Ye,Fang Xinyan,Zhang Yan,et al. Generalized assessment algorithm for power grid black-start modes[J]. Transactions of China Electrotechnical Society,2011,26(3): 155-161.

[7] 鐘慧榮,顧雪平. 基于模糊層次分析法的黑啟動方案評估及靈敏度分析[J]. 電力系統自動化,2010,34(16): 34-37.

Zhong Huirong,Gu Xueping. Assessment of power system black-start schemes based on fuzzy analytic hierarchy process and its sensitivity analysis[J]. Automation of Electric Power Systems,2010,34(16): 34-37.

[8] 林濟鏗,李童飛,趙子明,等. 基于熵權模糊綜合評價模型的電力系統黑啟動方案評估[J]. 電網技術,2012,36(2): 115-120.

Lin Jikeng,Li Tongfei,Zhao Ziming,et al. Assessment on power system black-start schemes based on entropy weighted fuzzy comprehensive evaluation model[J].Power System Technology,2012,36(2): 115-120.

[9] 吳燁,房鑫炎. 基于模糊 DEA 模型的電網黑啟動方案評估優化算法[J]. 電工技術學報,2008,23(8):101-106.

Wu Ye,Fang Xinyan. Data envelopment analysis based optimal fuzzy algorithm for assessing power grid black-start plans[J]. Transactions of China Electrotechnical Society,2008,23(8): 101-106.

[10] 張志毅,陳允平. 基于模糊多屬性決策的黑啟動方案優選[J]. 高電壓技術,2007,33(3): 42-45.

Zhang Zhiyi,Chen Yunping. Optimization of power system black-start schemes based on the fuzzy multiple attribute decision-making method[J]. High Voltage Engineering,2007,33(3): 42-45.

[11] 王宏,林振智,文福拴,等. 基于區間數的黑啟動決策方法[J]. 電力系統自動化,2013,37(11): 26-31.

Wang Hong,Lin Zhenzhi,Wen Fushuan,et al. A black-start decision-making method based on interval values[J]. Automation of Electric Power Systems,2013,37(11): 26-31.

[12] 林振智,文福拴,薛禹勝,等. 基于多屬性群決策特征根法的智能電網黑啟動決策[J]. 電力系統自動化,2010,34(5): 18-23.

Lin Zhenzhi,Wen Fushuan,Xue Yusheng,et al.Black-start decision-making in smart grids using mutiattribute group eigenvalue method[J]. Automation of Electric Power Systems,2010,34(5): 18-23.

[13] 林振智,文福拴,薛禹勝,等. 智能電網黑啟動群體決策的可靠性分析[J]. 電力系統自動化,2010,34(9): 17-22.

Lin Zhenzhi,Wen Fushuan,Xue Yusheng,et al.Reliability analysis on the group decision-making results of black-start strategies in smart grids[J].Automation of Electric Power Systems,2010,34(9):17-22.

[14] Liu Weijia,Lin Zhenzhi,Wen Fushuan,et al. Analysis and optimization of the preferences of decision makers in black-start group decision makering[J]. IET Generation,Transmission & Distribution,2013,7(1): 14-23.

[15] 林振智,文福拴,周浩. 熵權決策理論及其在黑啟動決策中的應用[J]. 電力系統及其自動化學報,2009,21(6): 26-33.

Lin Zhenzhi,Wen Fushuan,Zhou Hao. Entroy weight based decision-making theory and its application to black-start decision-making[J]. Transaction of Power Systemand Automation,2009,21(6): 26-33.

[16] 曾順奇,林振智,文福拴,等. 基于 Vague集理論的黑啟動決策模型與方法[J]. 電力系統自動化,2011,35(2): 18-22.

Zeng Shunqi,Lin Zhenzhi,Wen Fushuan,et al. A vague theory based model and approach for blackstart decision-making[J]. Automation of Electric Power Systems,2011,35(2): 18-22.

[17] 趙達維,劉天琪,李興源,等. 電網黑啟動方案評價指標體系及應用[J]. 電力系統自動化,2012,36(10): 7-12.

Zhao Dawei,Liu Tianqi,Li Xingyuan,et al. Blackstart scheme evalution indicator system and its application[J]. Automation of Electric Power Systems,2012,36(10): 7-12.

[18] 郭亞軍. 一種新的動態綜合評價方法 J]. 管理科學學報,2002,5(2): 49-54.

Guo Yajun. New theory and method of dynamic comprehensive evaluation[J]. Journal of Management Science in China,2002,5(2): 49-54.

[19] 郭亞軍,姚遠,易平濤. 一種動態綜合評價方法及應用[J]. 系統工程理論與實踐,2007,27(10): 154-158.

Guo Yajun,Yao Yuan,Yi Pingtao. A method and application of dynamic comprehensive evaluation[J].Systems Engineering Theory & Practice,2007,27(10):154-158.

[20] 郭亞軍,鐘田麗. 兼顧“功能性”與“均衡性”的綜合評價方法及應用[J]. 中國軟科學,2001(6):104-106.

Guo Yajun,Zhong Tianli. Multiple attribute evaluation method taking account of functionality and proportionality and its application[J]. China Soft Science,2001(6): 104-106.

[21] 歐陽森,石怡理,劉洋. 基于縱橫向拉開檔次法的電能質量動態評估[J]. 華南理工大學學報(自然科學版),2013,41(4): 27-32.

Ou Yangsen,Shi Yili,Liu Yang. Dynamic evaluation of power quality based on vertical and horizontal scatter degree method[J]. Journal of South China University of Technology(Natural Science Edition),2013,41(4): 27-32.

[22] X Gu,H Zhong. Optimization of network reconfiguretion based on a two-layer unit-restarting framework for power system restoration[J]. IET Generation,Transmission & Distribution,2011,6(7): 693-700.

[23] 王亮,劉艷,顧雪平,等. 綜合考慮節點重要度和線路介數的絡重構[J]. 電力系統自動化,2010,34(12): 29-33.

Wang Liang,Liu Yan,Gu Xueping,et al. Skeleton network reconfiguration based on node importance and line betweenness[J]. Automation of Electric Power Systems,2010,34(12): 29-33.