行星滾柱絲杠小轉角運動的動力學分析

王 樂，李海泓，張 玲

(中國空空導彈研究院，河南 洛陽 471009)

0 引 言

滾柱絲杠按其用途可分為行星滾柱絲杠(RSM)、差動式滾柱絲杠及循環式滾柱絲杠，其中行星滾柱絲杠具有很高的承載能力，能適應極高的速度加速度，且具有很高的穩定性［1］，因此在傳動進給系統中得到廣泛的應用。行星滾柱絲杠主要由五部分組成:絲杠、滾柱、螺母、持環及齒輪，如圖1 所示。

行星滾柱絲杠是把轉動運動形式轉化為軸向運動形式的機構，其與行星滾珠絲杠(BSM)結構相似，區別在于行星滾柱絲杠的載荷傳遞元件為螺紋滾柱，而非滾珠，相比于行星滾珠絲杠，行星滾柱絲杠的基礎表面具有更大的曲率半徑，而且接觸表面的數量也較多，這決定了行星滾柱絲杠擁有高壽命、大載荷及高速度運行能力。

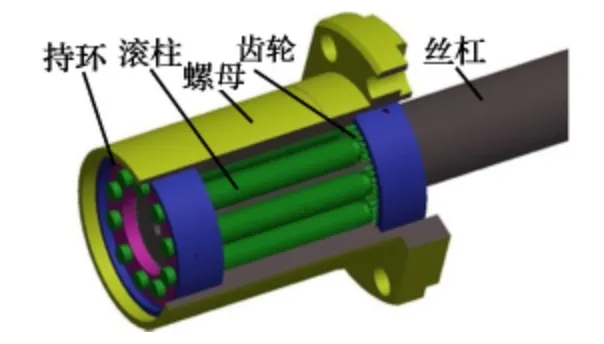
圖1 行星滾柱絲杠結構示意圖

行星滾柱絲杠一般應用在關鍵的、高精度機械里，如醫療器械［2－4］、航空航天工業［5－6］、光學裝置［7］、機器人及高精密度機床［8－9］。國內外對行星滾柱絲杠的研究日趨成熟，能夠得到廣泛的工業應用是建立在對行星滾柱絲杠效率、失效形式以及動態載荷試驗的深入研究的基礎之上;Velinsky［10］對行星滾柱絲杠的運動進行了研究，并給出了其效率隨螺紋螺旋角及接觸角變化規律。現有的研究主要集中在滾柱絲杠大轉角運動特性［11－12］，對小轉角運動中的動力學及受力特性研究還是一片空白。本文首先通過理論分析建立行星滾柱絲杠的數學模型，從彈性變形及傳動關系研究行星滾柱絲杠運行過程;其次建立行星滾柱絲杠的有限元模型，通過有限元顯式算法對行星滾柱絲杠進行動力學仿真，研究行星滾柱絲杠動力學響應。最終獲得行星滾柱絲杠的運動特性和動力學特性，為其工業應用提供了依據。

1 行星滾柱絲杠數學模型

行星滾柱絲杠在運行時，尤其是在小信號的絲杠轉動過程中，其軸向位移可以分為嚙合接觸彈性變形量和傳動軸向位移兩部分。

1.1 嚙合接觸彈性變形量

1.1.1 行星滾柱絲杠的赫茲理論模型

1896年，Hertz 在經典赫茲彈性接觸理論基礎上，進一步提出了關于兩彈性體點接觸的局部應力和變形的經典解［13］，經典赫茲理論建立在如下假設條件上:

a. 兩個接觸表面光滑，只能夠產生彈性變形，且服從胡克定律。對于行星滾柱絲杠，可以假設各部件的加工表面是光滑的，在額定載荷工作條件下，接觸點處產生的塑性變形量不超過各轉動體當量半徑的千分之一，這樣可以認為行星滾柱絲杠工作在彈性與塑性的臨界點處。

b. 等效接觸面的尺寸遠小于接觸的轉動體的表面曲率半徑。行星滾柱絲杠的嚙合運動中，絲杠與滾柱的接觸、滾柱與螺母的接觸都屬于點接觸，充分接觸之后相當于小面接觸，接觸面相比接觸體曲率半徑相當小，滿足假設。

c. 考慮接觸表面間的法向壓力載荷，不考慮接觸表面之間的切向摩擦力。行星滾柱絲杠屬高精度傳動裝置，可以忽略各傳動部件之間的摩擦力，把嚙合傳動過程簡化為正壓力接觸傳動。

用赫茲接觸理論方法求解點接觸，可以采用查表法獲得各參數數值，也可以根據接觸模型計算出的主曲率F(ρ)的值，經過迭代或插值積分得到系數ma，mb，K(e)，L(e)的值，再代入應力應變表達式中求出接觸問題的解。本文為了獲得較精確的赫茲接觸理論解，將結合數值積分、數值迭代兩種方法對赫茲理論的偏心方程進行求解，得到等效接觸橢圓的偏心率，進而得到接觸橢圓長短半軸，再代入到應力應變公式中得到赫茲理論解。計算時，輸入的參數有三個:行星滾柱絲杠基本結構參數、材料屬性及點接觸法相壓力載荷。

對于行星滾柱絲杠，簡化的赫茲點接觸模型如圖2 所示。在載荷Q 的作用下，螺紋嚙合接觸點將擴展成為一個接觸面。絲杠－滾柱嚙合點接觸及滾柱－螺母嚙合點接觸部分可以簡化為一個橢圓，橢圓長軸為2a，短軸為2b。

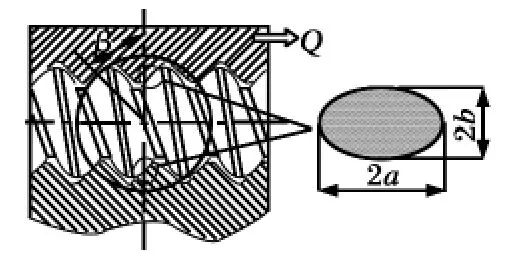
圖2 行星滾柱絲杠赫茲點接觸模型

長半軸a 及短半軸b 的表達式如下:

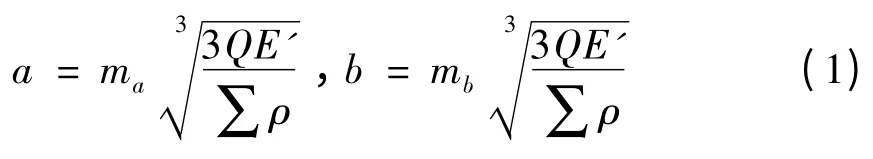
接觸橢圓的長短半軸系數分別為

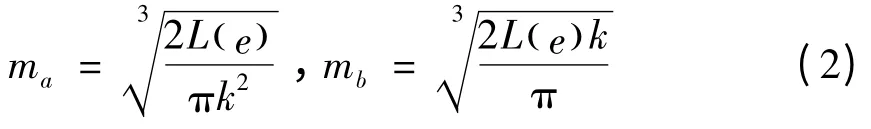
式中:k 為橢圓率，k=b/a;K(e)為第一類完全橢圓積分;L(e)為第二類完全橢圓積分。k(e)，L(e)可分別由下式求出:

根據赫茲理論，得到

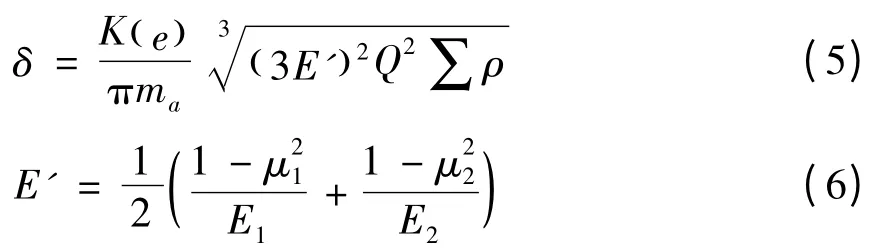
式中:Q 為法向壓力;δ 為接觸彈性趨近量;E'為當量彈性模量;E1，E2為兩接觸物體的彈性模量;μ1，μ2為兩接觸物體的泊松比;∑ρ 為兩物體在接觸點處的主曲率的和;橢圓偏心率e 與橢圓率k的關系為

主曲率函數F(ρ)由下式計算得到:

也可以表示為

若已知接觸物體在接觸點處的各個主曲率，則可以由式(7)或式(8)得到主曲率函數，然后進行數值迭代得到偏心率e，再得到長短半軸系數ma，mb，最后得到彈性趨近量δ。

1.1.2 嚙合接觸面曲率計算

行星滾柱絲杠副中絲杠與滾柱接觸時，其第一、二主曲率分別為

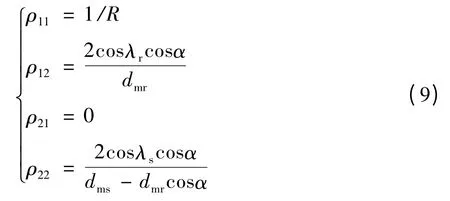
行星滾柱絲杠副中滾柱與螺母接觸時，其第一、二主曲率分別為

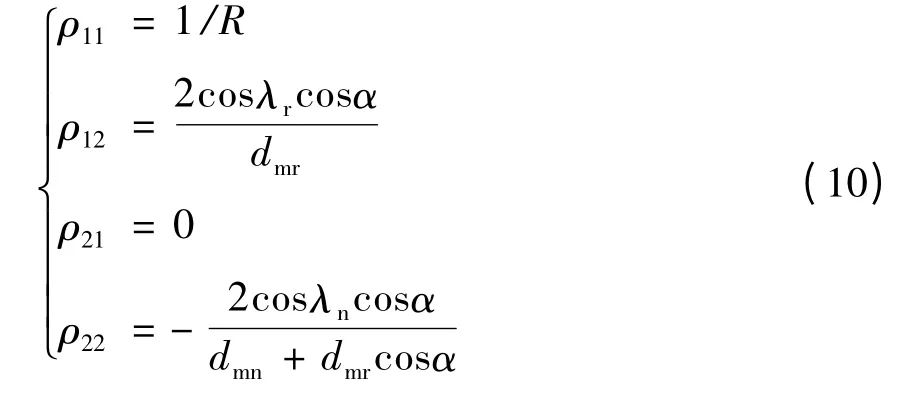
行星滾柱絲杠結構基本參數如表1 所示。

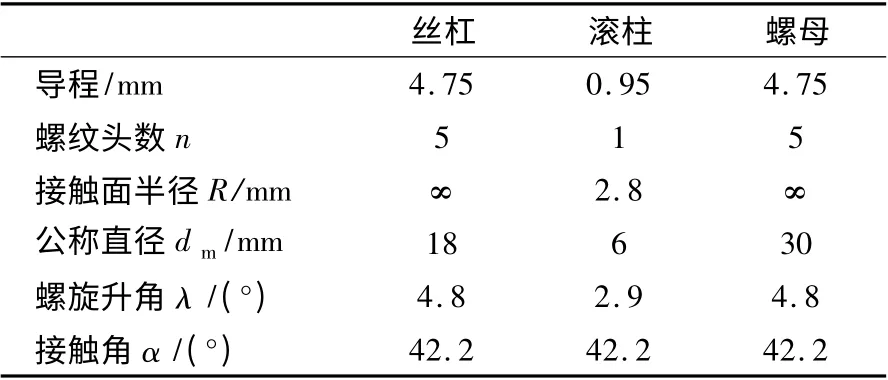
表1 行星滾柱絲杠基本結構參數

由公式(9)得絲杠－滾柱接觸主曲率ρ11=0.357 1，ρ12=0.246 6，ρ21=0，ρ22=0.108 9，進而可得絲杠－滾柱的主曲率函數如下:

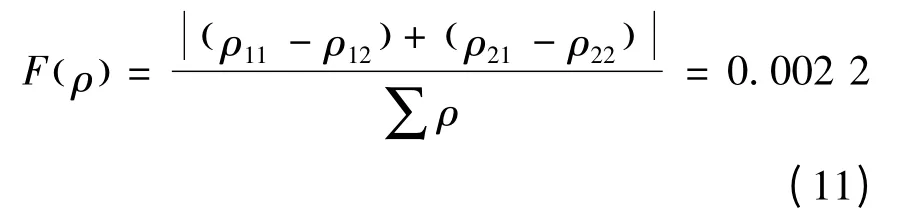
由公式(10)得滾柱－螺母接觸主曲率ρ11=0.357 1，ρ12=0.246 6，ρ21=0，ρ22=0.042 9，進而可得滾柱－螺母的主曲率函數如下:

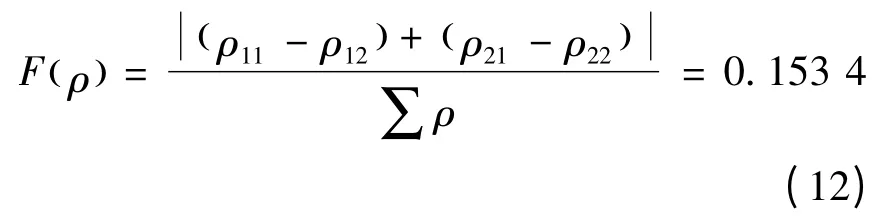
1.1.3 彈性變形量計算

行星滾柱絲杠材料選用42CrMo4，其材料性能參數:93 ℃時，彈性模量210 GPa，密度7 800 kg/m3，泊松比0.29。

對第一、第二類完全橢圓積分K(e)，L(e)，采用龍貝格(Romberg)積分法進行數值積分，積分表達式如下:

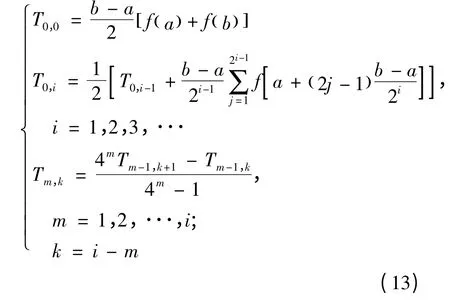
式中:a=0;b=π/2;Tm，k為2m－2 階牛頓－科特斯(Newton－Cotes)公式計算結果;對于第一類完全橢圓積分對于第二類完全橢圓積分

式中F(ρ)由式(11)～(12)計算得到，式(8)為關于橢圓偏心率e 的方程，編制數值積分及數值迭代的Matlab 程序求解得到e 值，將得到的e 值代入到式(5)中，可得最大彈性變形量δ。

a. 絲杠－滾柱點接觸理論求解

不同載荷軸向Q 作用下，絲杠－滾柱接觸橢圓面的長、短軸隨載荷的變化曲線如圖3 所示，接觸點彈性趨近量隨載荷的變化曲線如圖4 所示。

b. 滾柱－螺母點接觸理論求解

不同載荷軸向Q 作用下，滾柱－螺母接觸橢圓面的長、短軸隨載荷的變化曲線如圖5 所示，接觸點彈性趨近量隨載荷的變化曲線如圖6 所示。

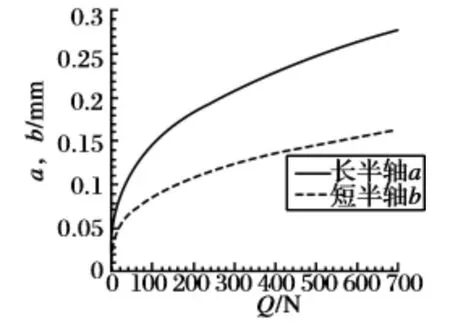
圖3 長、短軸變化曲線

圖4 彈性變形量變化曲線

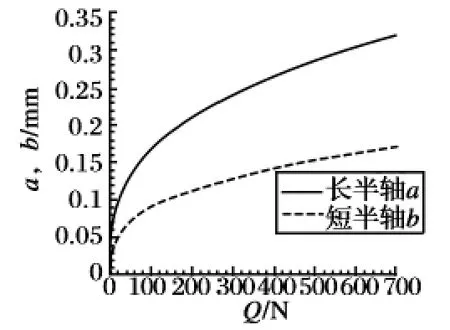
圖5 長、短軸變化曲線

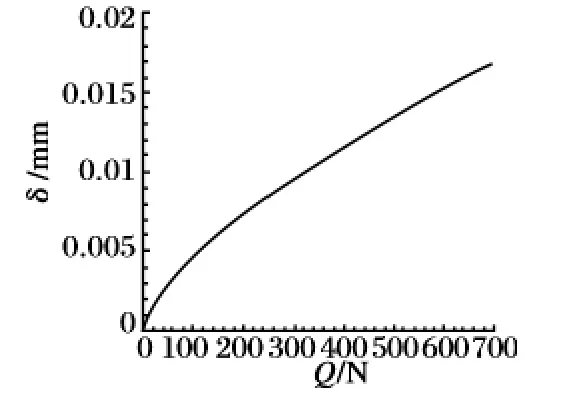
圖6 彈性變形量變化曲線

1.2 傳動軸向位移

行星滾柱絲杠三個轉動部件的節圓半徑影響相對轉速的大小，各部件的螺紋導程及螺紋旋向決定螺母的軸向進給量。絲杠與滾柱之間存在軸向位移差，但由于螺母與滾柱螺紋節距匹配及螺母持環的約束，滾柱相對于螺母無相對軸向位移，只做平面轉動。

1.2.1 行星滾柱絲杠無滑移傳動

行星滾柱絲杠副無滑移傳動形式如圖7 所示，絲杠與滾柱運動過程中相切于節圓切點B，滾柱與螺母相切于節圓切點A。

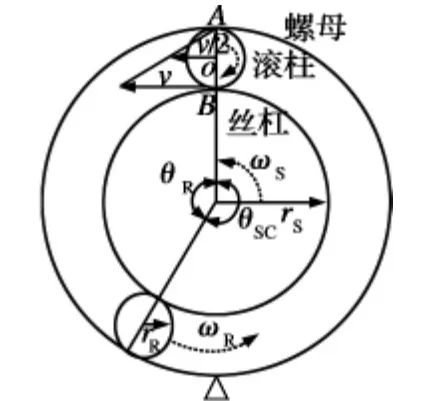
圖7 行星滾柱絲杠無滑移傳動

由于螺母無周向速度，故A 點周向速度為零;由于絲杠有自轉角速度ωS，故滾柱B 點的軸向速度如下式:

由運動關系可得，滾柱的圓心速度:

假設絲杠轉過θS角度，其節圓上B 點轉過的弧長為sB=rSθS，由圓心速度方程可知，滾柱中心O 轉過弧長為

約束點B 相應的轉角如下式:

式中:a 為絲杠與滾柱的中心距。

故行星滾柱絲杠的傳動關系為

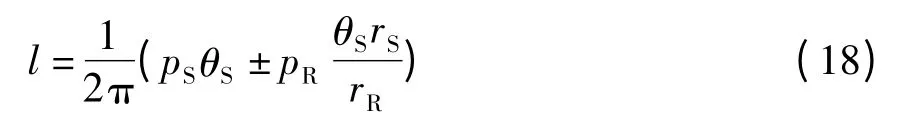
式中:l 為軸向傳動位移;pS為絲杠導程;pR為滾柱導程;當絲杠與滾柱螺紋旋向相同時取正號，當絲杠與滾柱螺紋旋向相反時取負號。

行星滾柱絲杠的結構參數代入式(18)，且本文采用的行星滾柱絲杠副絲杠與滾柱螺紋旋向相反，取負號得

1.2.2 行星滾柱絲杠有滑移傳動

當考慮行星滾柱絲杠副運動過程中絲杠與滾柱接觸嚙合滑動時，絲杠相對傳動螺母轉角為θ'SC，如圖8 所示。

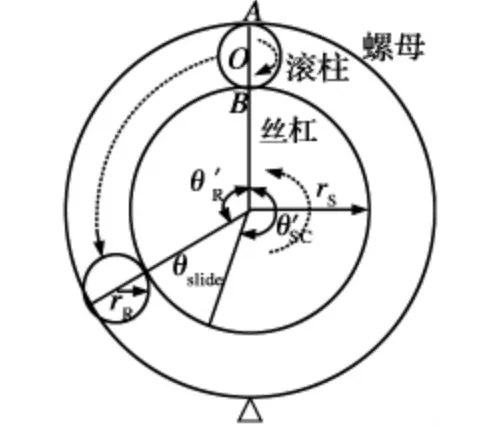
圖8 行星滾柱絲杠有滑移傳動

絲杠轉動2π 角度時，絲杠、滾柱、螺母轉角的關系滿足下式:

式中:θ'R為滾柱轉角;θ'SC為絲杠相對于螺母轉角;θ'S為絲杠轉角。

絲杠實際轉過角度與絲杠滑動轉角之間的關系如下式:

結合式(20)～(21)有:

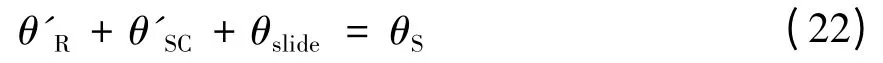
行星滾柱絲杠運動過程中，考慮嚙合滑動，滾柱轉角應小于沒有嚙合滑動條件下的轉角，絲杠滑動轉角小于沒有嚙合滑動條件下的轉角，用下面條件表示:

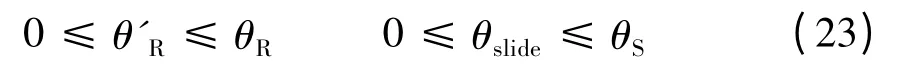
代入到上式有:0 ≤θ'SC≤θSC，查有關行星滾柱絲杠技術資料可知，在額定載荷下，絲杠滑動量與轉動量之間滿足關系式θslide= 0.005θS，有:

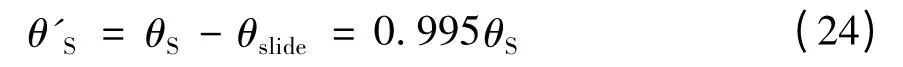
由式(24)可得行星滾柱絲杠副傳動關系如下式:

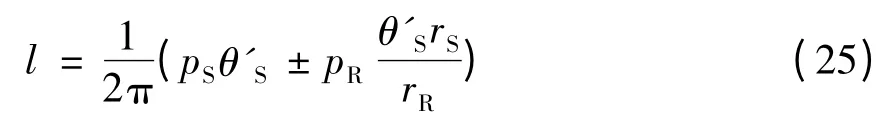
當絲杠與滾柱螺紋旋向相同時取正號，當絲杠與滾柱螺紋旋向相反時取負號。結合行星滾柱絲杠副結構參數得

2 行星滾柱絲杠有限元分析

2.1 行星滾柱絲杠有限元模型

行星滾柱絲杠的結構復雜，螺紋數量多，考慮到有限元計算效率，本文對行星滾柱絲杠的模型進行了簡化，如圖9 所示，取等長度的絲杠、滾柱及螺母接觸部分進行建模，模型中略去了滾柱中心圓柱部分及絲杠中心圓柱部分。

圖9 行星滾柱絲杠有限元模型

考慮行星滾柱絲杠螺紋結構的復雜性，螺紋接觸部分采用四面體網格劃分，設置C3D4 網格單元。每條螺紋面上三層網格，盡量減少網格數量，總網格數量為67 944。

定義行星滾柱絲杠材料密度為7.8E－9 ton/mm3，彈性模量為210 000 MPa，泊松比為0.29。螺紋嚙合接觸采用“surface－to－surface”小滑移接觸類型，切向庫倫摩擦系數為0.3，法向設置為硬接觸。

設置兩個分析步，第一個分析步施加預緊拉力，如圖10 所示，使螺紋嚙合充分接觸，第二個分析步施加絲杠扭矩，如圖11 所示，在扭矩作用下使滾柱、螺母轉動。第一個分析步中釋放滾柱及螺母軸向方向自由度，約束三個部件其他所有自由度，對螺母施加軸向預緊力，滾柱和螺母產生軸向位移;第二個分析步在第一個分析步基礎上，釋放絲杠、滾柱及螺母轉動方向自由度，在絲杠扭矩作用下三個部件產生角位移，滾柱和螺母有軸向位移。

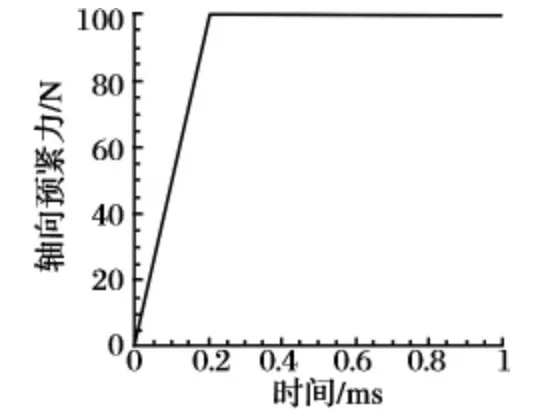
圖10 軸向預緊力曲線

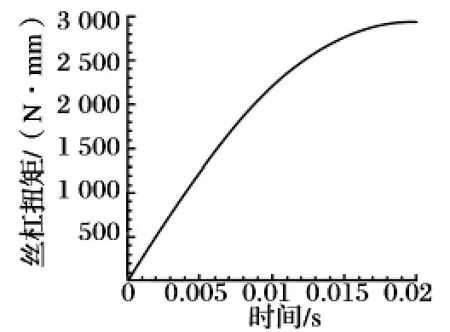
圖11 絲杠扭矩曲線

2.2 行星滾柱絲杠有限元仿真

對螺母施加如圖10 所示的預緊力，對絲杠施加如圖11 所示的扭矩載荷，總計算時間為0.001 s。計算完成后提取兩個時間點行星滾柱絲杠應力分布云圖，如圖12 ～13 所示。

圖12 0.000 313 6 s 時刻米塞斯應力分布

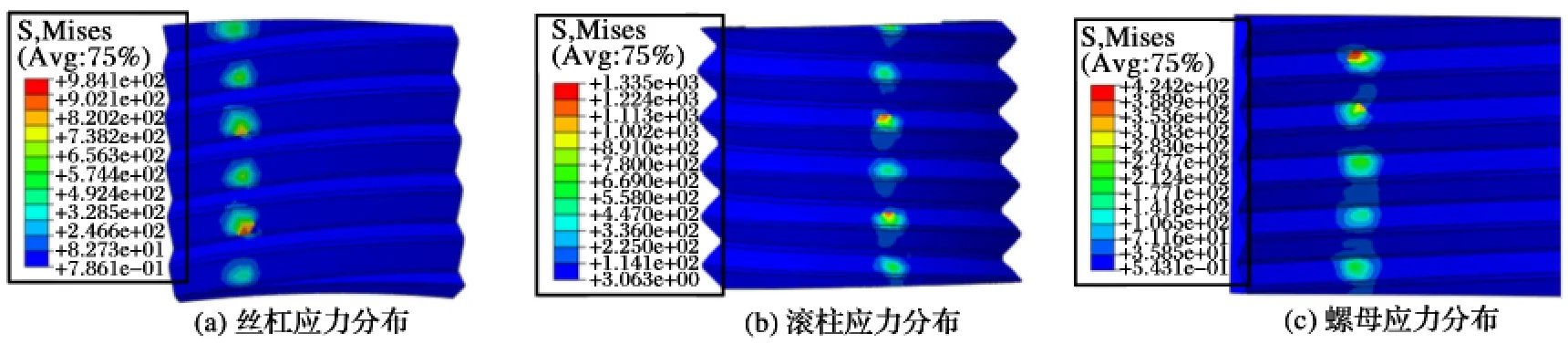
圖13 0.000 704 s 時刻米塞斯應力分布

從行星滾柱絲杠應力分布云圖可以看出，行星滾柱絲杠副運動過程中螺紋嚙合處接觸比較充分，各部件的應力分布比較均勻。從表2 中各部件最大米塞斯應力可知，絲杠與滾柱比螺母的最大應力大，這是因為絲杠與滾柱絲杠側的接觸螺紋的曲率較大，接觸更趨近于點接觸，0.000 313 6 s 時刻滾柱絲杠側及0.000 704 s 時刻絲杠與滾柱最大應力超過了材料屈服應力，材料局部進入塑性屈服。

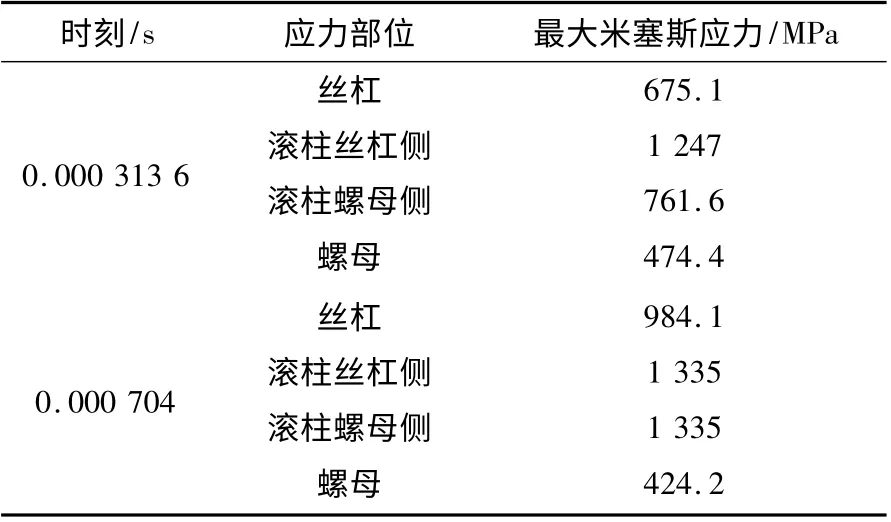
表2 行星滾柱絲杠最大應力分布

在0.000 2 s 之后，絲杠在扭矩作用下開始轉動，圖14(a)～(c)所示分別為絲杠角位移曲線、滾柱角位移曲線及螺母角位移曲線。滾柱的自轉方向與絲杠轉動方向相反，螺母與絲杠的轉動方向相反。

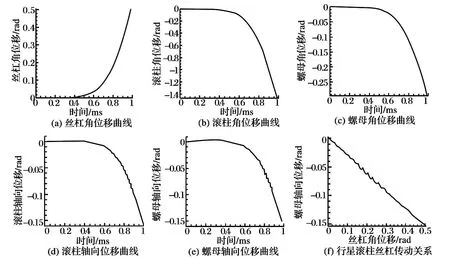
圖14 行星滾柱絲杠動力學響應曲線

圖14(d)～(e)分別為滾柱軸向位移曲線、螺母軸向位移曲線。0.000 2 s 時刻，螺母參考點受到的軸向拉力為100 N，平均分布在每個螺紋接觸點處的拉力為20 N，從圖中數據可得0.000 2 s 時刻滾柱軸向位移為0.001 640 42 mm，與赫茲理論分析得到的彈性變形量0.001 6 mm 相比，相對誤差為2.5%。0.000 2 s 時刻之后，滾柱及螺母最大正向軸向位移在0. 000 284 8 s 時刻達到，分別為0.001 767 59 mm，0.003 402 09 mm。在實際進給傳動系統中，在預緊力作用下的螺母的正向軸向位移需作為補償引入到運動模型中。

圖14(f)為螺母軸向位移在0.000 2 s 之后隨絲杠角位移變化曲線，即行星滾柱絲杠傳動關系曲線。從圖中得到曲線斜率為0.300 010，與理論分析得到的有滑移條件下的螺母軸向位移隨絲杠角位移變化率0.300 882 4 符合很好，誤差只有0.29%。

3 結 論

本文首先根據實際應用中的小轉角運動建立了行星滾柱絲杠的數學模型，把行星滾柱絲杠的軸向位移分解為嚙合接觸彈性變形量和傳動軸向位移，用Hertz 接觸理論求解了不同載荷下嚙合接觸彈性變形量，并推導了行星滾柱絲杠傳動關系;在此基礎上建立了行星滾柱絲杠的有限元模型，通過有限元仿真獲得了行星滾柱絲杠的動力學響應。主要研究結論如下:

a. 在一定預緊力下，行星滾柱絲杠螺紋嚙合處發生彈性變形，在行星滾柱絲杠精確控制系統的實際應用中應對這部分彈性變形量進行補償。

b. 通過有限元方法獲得了行星滾柱絲杠螺紋嚙合點接觸的應力分布及各部件的動力學響應曲線，結合理論推導的傳動比，為行星滾柱絲杠在進給系統的實際應用提供了依據。

［1］Lemor P C. The Roller Screw，an Efficient and Reliable Mechanical Component of Electro－Mechanical Actuators［C］// Energy Conversion Engineering Conference，IEEE，1996，1:215－220.

［2］Andrade A，Nicolosi D，Lucchi J，et al. Auxiliary Total Artificial Heart:A Compact Electromechanical Artificial Heart Working Simultaneously with the Natural Heart［J］.Artif Organs，1999，23(9):876 –880.

［3］Richenbacher W E，Pae W E Jr，Magovern J A，et al.Roller Screw Electric Motor Ventricular Assist Device［J］.Transactions on American Society for Artificial Internal Organs，1986，32(1):46 –48.

［4］Rosenberg G，Snyder A，Weiss W，et al. A Roller Screw Drive for Implantable Blood Pumps［J］.Transactions on American Society for Artificial Internal Organs，1982，28:123 –126.

［5］Gromov V V，Misckevich A V，Yudkin E N，et al. The Mobile Penetrometer，a“Mole”for Sub－Surface Soil Investigation［C］//Proceedings of the Seventh European Space Mechanisms and Tribology Symposium，Noordwijk，the Netherlands，1997:151 –156.

［6］Wander J，Byrd V，Parker J .Initial Disturbance Accommodating Control System Analysis for Prototype Electromechanical Space Shuttle Steering Actuator［C］//Proceedings of the American Control Conference，Seattle W A，1995，6:3961 –3964.

［7］Marks S，Cortopassi C，Devries J，et al. The Advanced Light Source Elliptically Polarizing Undulator［C］//Proceedings of the Particle Accelerator Conference，Canada，1997，3:3221 –3223.

［8］Brandenburg G，Bruckl S，Dormann J，et al. Comparative Investigation of Rotary and Linear Motor Feed Drive Systems for High Precision Machine Tools［C］//Proceedings of the Sixth International Workshop on Advanced Motion Control，Nagoya，Japan，2000:384 –389.

［9］Dupont P E. Friction Modeling in Dynamic Robot Simulation［C］//Proceedings of the IEEE International Conference on Robotics and Automation，Cincinnati，1990，2:1370 –1376.

［10］Velinsky S A，Chu B，Lasky T A. Kinematics and Efficiency Analysis of the Planetary Roller Screw Mechanism［J］. Journal of Mechanical Design，2009，131(1):1－8.

［11］陳芳. 兩級行星滾柱絲杠傳動設計與精確度研究［D］.南京:南京理工大學，2009.

［12］韋振興. 行星滾柱絲杠副剛度及效率的分析與研究［D］.武漢:華中科技大學，2011.

［13］Harris T A，Kotzalas M N. Essential Concepts of Bearing Technology［M］. CRC Press，1978:106－109.