高速旋轉固體火箭發動機噴管受熱狀態計算
郝 雯,馬聰慧,邵躍躍
(中國空空導彈研究院,河南 洛陽 471009)
0 引 言
在固體火箭發動機中,通常會發生熱傳遞和質量傳遞的綜合過程,該過程伴隨有吸熱或放熱的化學反應。在固體火箭發動機噴管壁的熱交換過程中,同時存在著導熱、熱對流和熱輻射這三種基本熱量傳遞方式。火箭推進劑在燃燒時,燃氣通過熱對流、熱輻射和凝聚相微粒的直接接觸導熱,將熱量傳遞給噴管壁內表面;被加熱的噴管壁以熱傳導的方式,將熱量由內表面經過噴管壁向外表面傳遞;通過熱對流和熱輻射,熱量由外表面向周圍空間散失[1-4]。
固體火箭發動機噴管的傳熱過程十分復雜,包括熱傳導、熱輻射、熱對流。實際上,發動機噴管的熱狀態除與噴管初始條件相關之外,還與發動機噴管的結構、材料物性參數等也有關系[5-6]。實際計算過程中,由于無法提前給出噴管壁面的熱邊界條件,同時還要考慮換熱中的輻射效應,所以,噴管傳熱計算必須當作是耦合的傳熱問題來進行求解。
高速旋轉的工況會縮短固體火箭發動機的燃燒時間,增加推力與壓強,對發動機的傳熱造成嚴重的影響[7],此外高速旋轉所致的強旋流動現象也對發動機結構的熱防護帶來負面效應。因此,計算高速旋轉工況下的固體火箭發動機噴管受熱狀態是十分有意義的。
1 噴管喉部換熱數值模型
本文建立了噴管流固熱耦合的換熱模型:先進行發動機噴管內流場數值模擬,之后將高精度的計算結果與噴管固壁的溫度場計算相耦合,其中考慮固壁中的熱傳導、內流場與噴管壁面的湍流換熱以及包含吸收-發射性氣體介質的熱輻射交換,并給予噴管構型將該換熱模型應用與軸對稱噴管的流場與溫度場的解算。考慮噴管構型的軸對稱性,為了減少數值仿真過程中的計算量,建立二維軸對稱數值模型。
二維軸對稱[8-9]質量守恒方程如下:
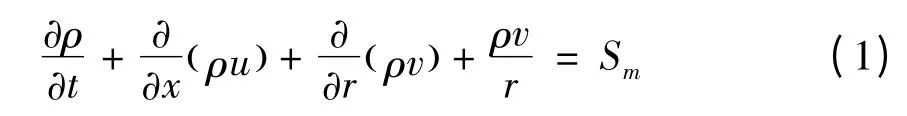
上述方程是二維軸對稱的質量守恒方程,該方程適用范圍包括:可壓和不可壓流動。式(1)中x是軸向坐標,r 是徑向坐標,u 和v 分別是軸向和徑向的速度分量,源項Sm是稀疏相增加到連續相中的質量或其他加質流動中增加的質量。
對于二維軸對稱流場,建立考慮旋流在內的軸向和徑向的動量守恒方程,如下:
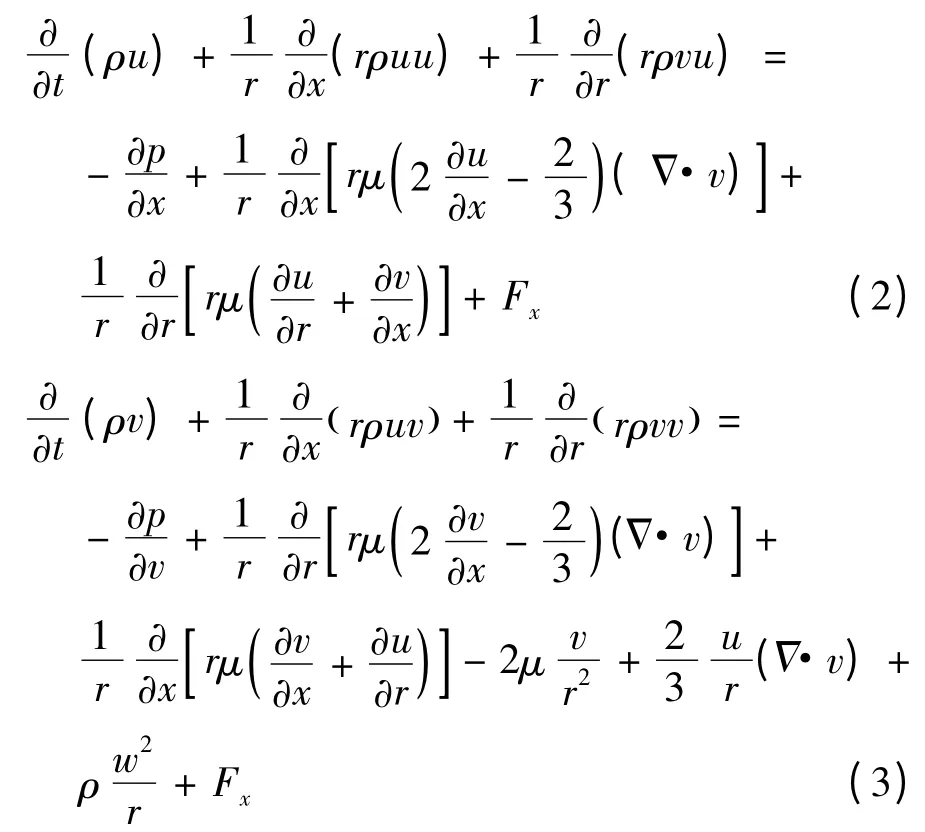
噴管喉部換熱模型的能量守恒方程包含流體換熱、流固耦合換熱以及固體內部的熱傳導等,流固耦合界面處的輻射換熱以及湍流邊界層內的粘性換熱對固體內部的熱結構分布影響較大[10],必須加以建模分析。能量守恒方程如下:
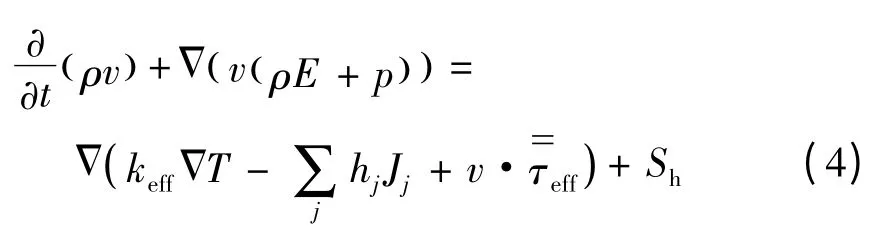
式中:keff= k + ki為有效熱導率,ki為湍流引起的導熱率,由采用的湍流模型以及壁面函數確定[11]。式(4)右端的前三項分別表示由于熱傳導、組分擴散、粘性耗散引起的能量轉移,源項是由于化學反應、輻射等其他因素引起的熱源。
在固體區域,能量控制方程如下:
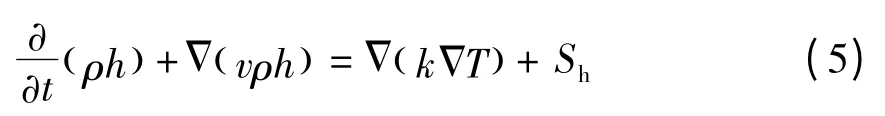
式中,速度v 表示固體區域由于旋轉或平移等運動的速度。式(5)右端第一項表示熱傳導引起的熱流,第二項即源項表示固體區域的內熱源。
式(1)~(5)是二維軸對稱噴管喉部流固耦合換熱數值仿真模型的基本控制方程,通過求解方程組可以獲取噴管喉部計算域內的溫度場、壓力、速度場等分布,為噴管喉部換熱研究提供數據支持。
2 發動機噴管受熱狀態數值計算
對噴管在靜態和旋轉條件下的受熱狀態做計算研究,對轉速為0 r/min,4 000 r/min,8 000 r/min 時進行流固熱耦合數值模擬。
2.1 轉速為0 r/min 時噴管受熱狀態計算
取燃燒室平均壓強7.19 MPa 為入口條件,45#鋼給定密度7. 85 ×103 kg/m3,比熱給定450 J/(kg·K),導熱系數給定35 W/(m·K),進行非穩態傳熱計算,時間步長取0.1 s,計算5 s 內噴管中燃氣的流動與換熱。
不同時刻噴管溫度云圖如圖1 所示。
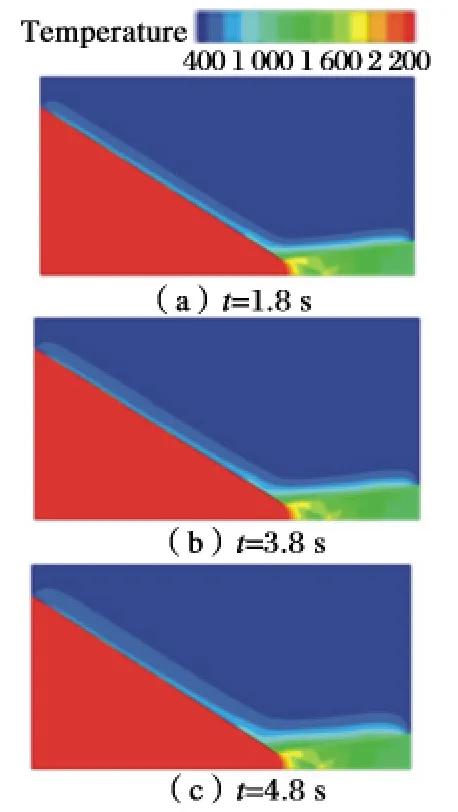
圖1 0 r/min 時不同時刻溫度云圖
隨著發動機工作時間的延續,噴管壁面的溫度處于持續上升狀態,噴管壁面的溫度傳遞呈二維特性,靠近噴管內壁面溫度相對較高。
表1 是轉速為0 r/min 時,發動機在1.8 s,3.8 s,4.8 s 時不同位置的熱流密度值。分別取三個觀測點,噴管收斂段(x =40 mm)、噴管喉部(x=85 mm)、噴管擴張段(x=100 mm)處,得到該點處熱流密度的值。
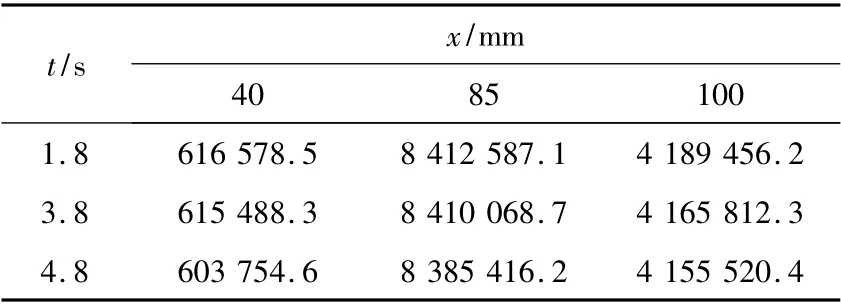
表1 0 r/min 時 不同時刻壁面總熱流密度表(W/m2)
由上表可知,噴管喉部區域總熱流密度最大,表示噴管喉部換熱最為強烈。因此,喉部前端部分區域溫度最高,收斂段溫度逐漸降低。而不同時刻t=1.8 s,t=3.8 s,t =4.8 s 時,燃氣側對噴管壁面熱交換的總熱流密度逐漸降低,發動機噴管喉部位置的總熱流密度最大,換熱最為強烈,當發動機工作1.8 s 時,可達8 400 000 W/m2以上。由于噴管喉部燃氣流動變化劇烈,因此總熱流密度變化大,在噴管的收斂段和擴張段,熱流密度均比喉部熱流密度要低。
由計算區域溫度云圖可知,噴管壁面的溫度傳遞呈二維特性,靠近噴管內壁面溫度相對較高,噴管喉部區域換熱最為強烈,這也與不同時刻壁面總熱流密度示意圖相對應。喉部區域熱流密度最大。因此,喉部前端部分區域溫度最高,收斂段溫度逐漸降低。
2.2 轉速為4 000 r/min 時噴管受熱狀態計算
取燃燒室平均壓強25. 54 MPa 為入口條件,其他條件與2.1 節同,計算5 s 內噴管中燃氣的流動和換熱。
不同時刻噴管溫度云圖如圖2 所示。
表2 是轉速為4 000 r/min 時,發動機在0.5 s,1.5 s,3.0 s 時不同位置的熱流密度值。分別取噴管收斂段(x=40 mm)、噴管喉部(x=85 mm)、噴管擴張段(x=100 mm)三個點計算熱流密度的值。
由于在高速旋轉狀態下,發動機噴管內壓強增加,導致噴管內壁面的熱流密度增加,壁面溫度升高。熱流密度的變化規律與0 r/min 時大致相同,在噴管喉部達到峰值。在噴管的收斂段和擴張段,隨著到噴管喉部距離逐漸增加,熱流密度逐漸減小。
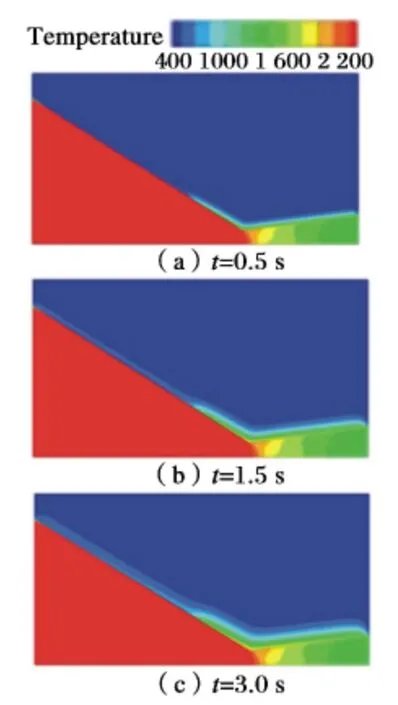
圖2 4 000 r/min 時不同時刻溫度云圖
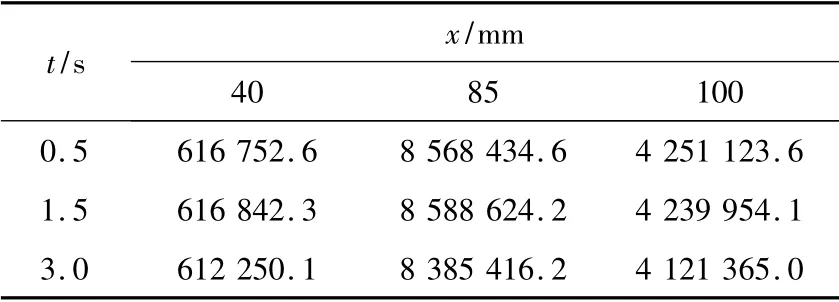
表2 4 000 r/min 時不同時刻壁面總熱流密度表(W/m2)
2.3 轉速為8 000 r/min 時噴管受熱狀態計算
取燃燒室平均壓強41.92 MPa 為入口條件,其他條件與2.1 節同,計算5 s 內噴管中燃氣的流動與換熱。
不同時刻噴管溫度云圖如圖3 所示。
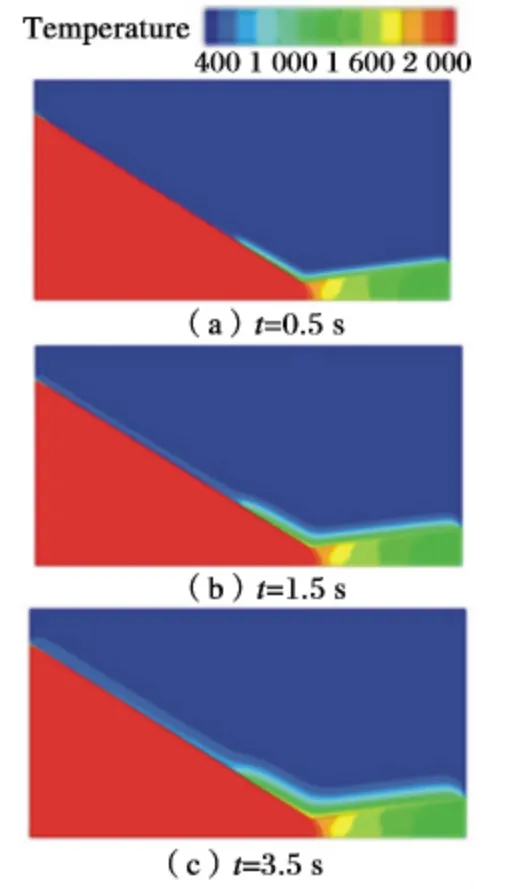
圖3 8 000 r/min 時不同時刻溫度云圖
表3 是8 000 r/min 時,發動機在0.5 s,1.5 s,3.5 s 時不同位置的熱流密度值。分別取噴管收斂段(x=40 mm)、噴管喉部(x =85 mm)、噴管擴張段(x=100 mm)三個觀測點,計算熱流密度的值。
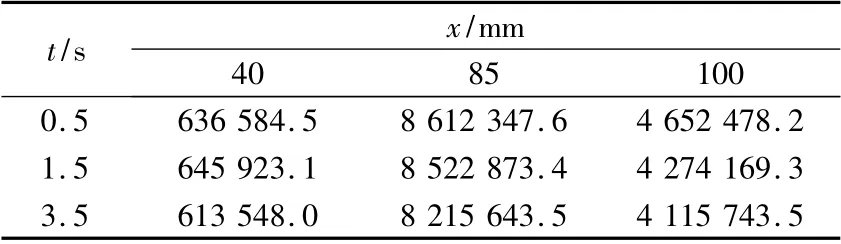
表3 8 000 r/min 時 不同時刻壁面總熱流密度表(W/m2)
在8 000 r/min 的轉速下,由于壓強,溫度等綜合作用,溫度傳遞與熱流密度的變化與前兩節變化相同。
2.4 對比分析
不同時刻的溫度對比云圖于前幾節所示,噴管壁面收斂段、直線段以及擴張段不同位置的溫度均逐漸上升。不同時刻下噴管內壁面溫度均在噴管喉部前端達到最大值,在噴管收斂段以及擴張段壁面溫度均呈現下降趨勢。
對比分析同一工況下溫度場分布圖可知,噴管喉部流場流動區域的溫度在不同時刻變化不大,而噴管內壁面的溫度隨著發動機的熱交換程度增大以及發動機工作時間的延續而逐漸增加,因此發動機喉部燃氣側對噴管喉部內壁面的熱交換程度隨時間逐漸改變。
由表1 ~3 可知,發動機隨著工作時間的延續,燃氣側對噴管內壁面熱交換的總熱流密度逐漸降低,發動機噴管喉部前端位置總熱流密度最大,換熱最為強烈。
燃氣側對噴管壁面熱交換的對流換熱系數主要由燃氣物性參數影響[12],基本不隨發動機工作時間改變而改變,在噴管喉部前端處,分子活動最為劇烈,導致對流換熱系數最大,對流換熱最為強烈。在噴管擴張段,隨著發動機工作時間的延續,流場流動逐漸發展,對流換熱系數略有上升。但與噴管喉部換熱系數相比要低于喉部數值。
高速旋轉對發動機壁面換熱的影響總趨勢是隨著旋轉過載的加大而增加。發動機燃氣切向速度顯著增加,單位時間內流過壁面的燃氣分子數增多,對流換熱系數增大,導致對流換熱加劇。在燃燒室及噴管區域,均產生了燃氣渦旋,燃氣所具有的部分動能在渦旋中逐漸耗散轉變為熱能,壁面的傳熱加強。
圖4 為文獻[13]中的高速旋轉發動機試驗結果,由文獻可知,在高速旋轉條件下,噴管內表面型面有明顯的燒蝕,特別是喉襯鑲嵌接縫處。噴管內燃氣流速高、單位截面積的質量流率大,使得噴管壁所受到的高溫高壓燃氣的加熱作用十分嚴重,從而造成噴管材料的嚴重燒蝕。燒蝕現象隨著轉速的提高而愈加嚴重,與數值計算結果相對應。

圖4 高速旋轉實驗發動機喉部照片
結合發動機高速旋轉時的內流場流線示意圖5分析。由于實際固體推進劑在燃燒過程中,將產生一定量的凝聚相微粒。這些凝聚相微粒的存在,對傳熱產生影響。高溫凝聚相微粒的導熱性較氣相高,對壁面通過撞擊直接接觸進行熱傳導。
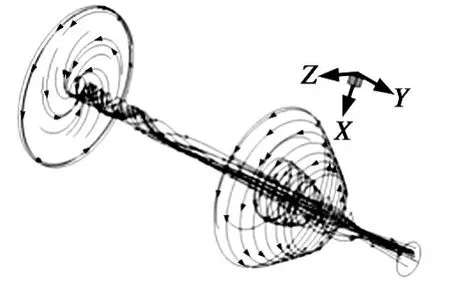
圖5 10 000 r/min 時發動機流場流線圖
同時,回旋渦流加劇了高溫燃氣中凝相粒子的沉積和積聚,這些粒子凝固后的積屑和積瘤導致發動機內部噴管熱傳遞效應加劇,凝相粒子與高溫高壓燃氣產生的渦流共同沖刷該區域。
文獻[13]中噴管座螺紋連接處、噴管進口端和出口端均有明顯的金屬流動痕跡和熔化。文獻[14]中發動機前封頭處被燒穿,也驗證了凝相粒子對壁面的傳熱影響,與數值模擬結果相符。
這些現象的揭示對固體火箭發動機的熱防護設計提出了更高的要求。
3 結 論
本文建立了二維非定常噴管壁面流固熱耦合模型,計算噴管受熱狀態、熱流密度等參數。計算結果表明,隨著發動機工作時間的延續,高溫燃氣對噴管內壁面熱交換的總熱流密度逐漸降低,發動機噴管喉部前端位置總熱流密度最大,換熱最為強烈。
高速旋轉對發動機噴管壁面傳熱影響的趨勢是隨著旋轉過載的增大而增大。發動機燃氣切向速度顯著增加,單位時間內流過壁面的燃氣分子數增多,使對流換熱系數增大,導致對流換熱加劇。在噴管區域,產生了燃氣渦旋,燃氣所具有的部分動能在渦旋中逐漸耗散轉變為熱能,壁面的傳熱加強。高速旋轉對噴喉結構強度與熱防護帶來嚴重影響。
[1]Cortopassi A C,Boyer E,Acharya R,et al. Design of a Solid Rocket Motor for Characterization of Submerged Nozzle Erosion[C]// 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit,AIAA 2008-4889,2008.
[2]Klager K.The Interaction of the Efflux of Solid Propellants with Nozzle Materials[J]. Propellants and Explosives,1997,2(3):55-63.
[3]劉玉磊.燃氣舵流固耦合傳熱數值分析[J].航空兵器,2013 (3):41-43.
[4]王偉,王德升.噴管擴張段絕熱層的燒蝕計算[J].固體火箭技術,1999,22(3):16-19.
[5]Wilcox D C.Turbulence Modeling for CFD[M].La Canada,California,DCW,1998. Industries,Inc,1998.
[6]Lien F S ,Leschziner M A. Assessment of Turbluent Transport Models Including Non-Linear RNG Eddy-Viscosity Formulation and Second-Moment Closure[J].Computers and Fluids,1994,23(8):983-1004.
[7]Caveny L H. Extension to Analysis Ignition Transients of Segmented Solid Rocket Booster[R]. NASA-CR-150632,1978.
[8]陶文銓.數值傳熱學[M].西安:西安交通大學出版社,1988.
[9]Patankar S V.傳熱與流體流動的數值計算[M]. 張政,譯.北京:科學出版社,1984.
[10]Golasfhani M. Computation of Two-Phase Viscous Flow in Solid Rocket Motors Using a Flux-Split Eulerian-Lagrangian Technique[R].AIAA 1989-2178,1989.
[11]王福軍.計算流體動力學分析——CFD 軟件原理與應用[M].北京:清華大學出版社,2004.
[12]鄭亞,陳軍,鞠玉濤,等. 固體火箭發動機傳熱學[M]. 北京:北京航空航天大學出版社,2006.
[13]王棟,余陵,武曉松. 固體火箭發動機高速旋轉試驗研究[J]. 彈道學報,2004(4):87-91.
[14]邵愛民.大型固體發動機旋轉試車頭部熱防護工程分析[J].固體火箭技術,1998(3):7-12.

