三相電壓型整流器模型電壓預測控制

王 萌 施艷艷 沈明輝 王海明 逯亞瑩 祁明艷

（1. 河南師范大學物理與電子工程學院 新鄉 453007 2. 國網新鄉供電公司 新鄉 453000）

0 引言

隨著微處理器技術的迅速發展，模型預測控制（Model Predictive Control，MPC）在功率變換器及電力傳動中的應用得到了廣泛研究[1-4]。MPC利用功率變換器的離散特性，根據控制對象數學模型，在每個控制周期內對所有開關狀態作用下的輸出結果進行預測。算法引入價值函數對預測結果進行評估，并選擇最優的開關狀態作為控制器輸出。控制系統運行中不包含線性控制器和調制器，具有動態響應速度快、內部完全解耦、多變量靈活控制等優點[5-7]。

MPC算法在每個控制周期內只輸出一種開關狀態，為獲得較快的響應速度和良好的控制品質，MPC的控制周期一般較短[8,9]。雖然MPC結構簡單，但相對于很短的控制周期，其循環預測和尋優過程較為復雜，運算量較大，對控制器的計算性能要求較高。同時，預測和尋優過程耗時較長不利于其他輔助控制算法的擴展，影響 MPC的工業化應用。另外，隨著開關狀態的增多，如多電平變換器、矩陣變換器等，MPC算法的運行時長也隨之增加，這將造成控制周期時長增加，進而影響變換器的控制效果[10,11]。因此，在保證控制器響應速度和控制品質的前提下，有效縮短預測和尋優耗時至關重要[12]。為了縮短MPC算法的計算耗時，文獻[13]提出一種通過分區對 MPC預測過程進行簡化的方法，可有效減少控制算法運行時長，提高算法的運行效率，但該算法將對 MPC的部分控制性能造成影響。文獻[14]針對級聯型H橋逆變器的模型預測控制，提出了一種簡化的控制算法，獲得了較好的效果。

本文以三相電壓型 PWM 整流器[15]（Voltage Source Rectifier，VSR）為例，提出一種計算耗時較少的模型電壓預測控制。首先，根據VSR模型和電流參考值獲得下一時刻需要的輸出電壓參考值；通過對模型電流預測控制中的價值函數進行等效變換，獲得基于輸出電壓的價值函數表達式；最后，采用矢量分區的方法選擇最優的輸出電壓矢量。針對三相VSR系統，所提模型電壓預測控制方法可將模型電流預測控制方法中每個控制周期內的8次預測過程、8次價值函數計算和7次比較過程簡化為1次預測過程、1次點乘和 1次判斷過程。因此，控制算法結構簡單、運算量小、計算時間顯著縮短，保證了控制系統的響應速度和穩定運行。通過仿真和實驗證明所提算法的正確性和有效性。

1 模型電流預測控制原理

三相電壓型PWM整流器主電路如圖1所示。

圖1中，uga、ugb、ugc為三相交流側電壓；uca、ucb、ucc為整流橋輸入側三相電壓；udc為直流側電壓；ia、ib、ic為三相交流電流；iL為負載電流；Rg為線路等效電阻；Lg為進線電感；C為直流電容；RL為直流側負載。

通過坐標變換將三相 VSR的數學模型轉換到兩相靜止坐標系中，可得

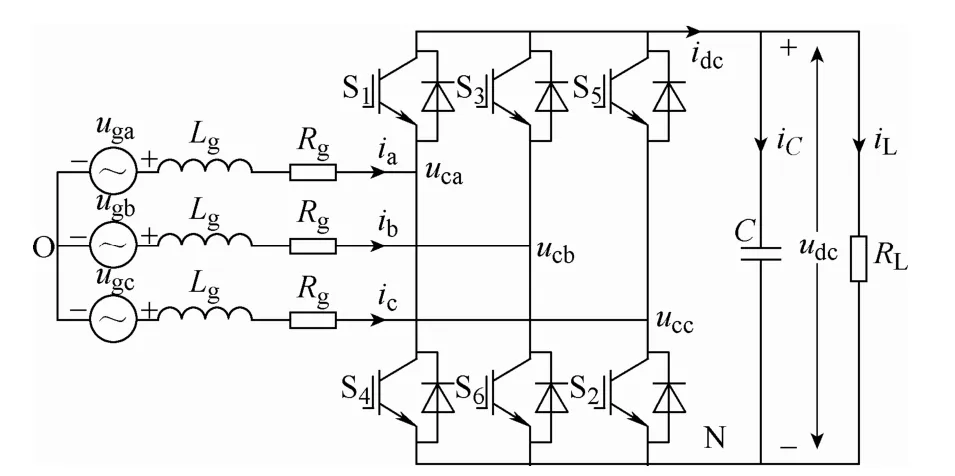
圖1 三相電壓型PWM整流器主電路Fig.1 Topological structure of main circuit of three-phase voltage source PWM rectifier

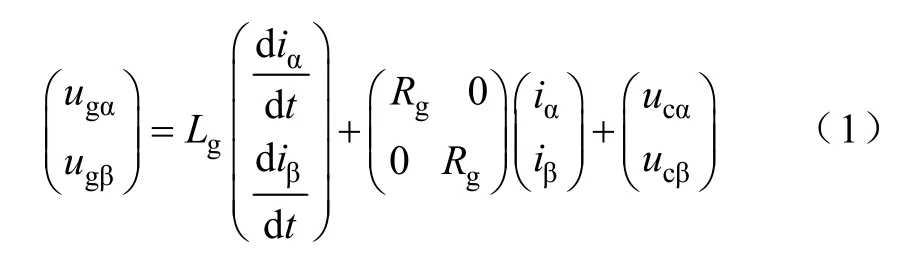
式中，ugα、ugβ分別為α、β軸電網電壓；ucα、ucβ、iα、iβ分別為整流器α、β軸輸入電壓、電流。

將式（1）離散化，可得

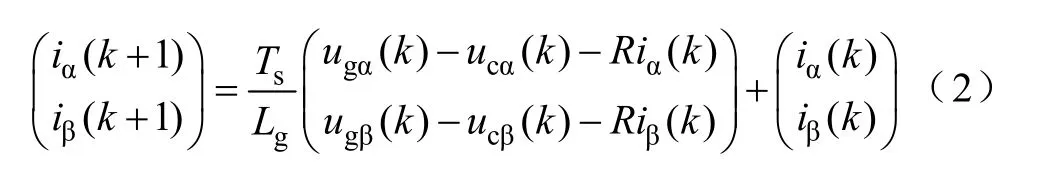
為模型預測控制算法定義價值函數，即

模型電流預測控制策略利用功率變換器件開關狀態的有限性，根據控制對象的離散數學模型預測在不同開關狀態作用下輸入電流的未來值。算法采用價值函數對預測結果進行評價，并選擇使價值函數最小的電壓矢量作為控制器的輸出。

采用模型電流預測控制算法的三相電壓型整流器控制結構如圖2所示。

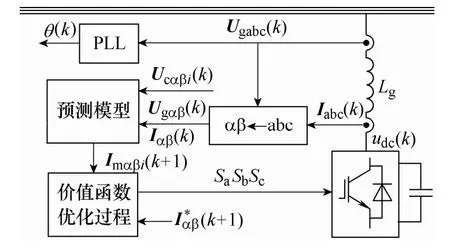
圖2 基于MPC策略的VSR控制結構Fig.2 VSR control structure based on MPC scheme

系統運行時首先將電壓Ugabc(k)通過鎖相環（Phase Locked Loop，PLL）得到電網電壓角度θ(k)，θ(k)可作為Park反變換角度；通過坐標變換將三相電壓Ugabc(k)、電流Iabc(k)轉換為兩相靜止坐標系下的電壓Ugαβ(k)、電流Iαβ(k)；通過VSR的離散預測模型，分別對k+1時刻8個電壓矢量Ucαβi(k)作用下的輸入電流Imαβi(k+1)進行預測；通過價值函數對8個預測結果進行評價，最終選擇最優的開關狀態作為k+1時刻功率變換器的控制信號。算法在每個控制周期循環一次，每個周期內電流控制算法需要進行8次電流預測、8次價值函數計算（16次乘法運算、24次加減運算）和7次比較過程才能得出最優的電壓矢量。

2 模型電壓預測控制算法

模型預測控制算法在每個控制周期循環一次，因此，算法運行時間需足夠短以獲得較高的采樣頻率。為了縮短算法的運行時間，需要降低算法的復雜程度。本文提出一種模型電壓預測控制算法對傳統模型電流預測控制算法進行簡化。

由式（1）可得離散化后的VSR系統電壓方程為

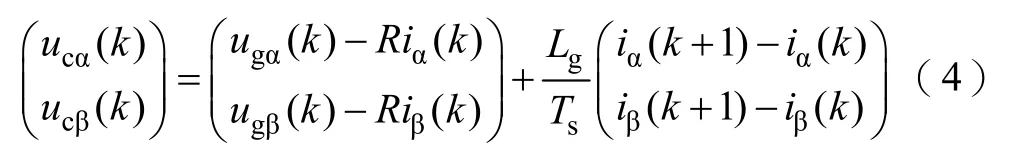
由式（4）可知，若系統輸入電流在k+1時刻能夠跟蹤參考電流(k+1)、(k+1)，則需要的輸入電壓(k)、(k)為

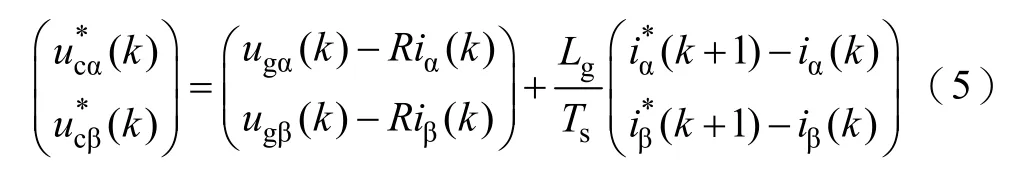
由式（5）可知，采用k+1時刻的參考電流對所需輸入電壓進行預測，則采用一次預測即可完成。與模型電流預測相比，電壓預測將省去7次預測過程。

根據k時刻電網電壓、電流及8個輸入電壓，通過式（1）可得到k+1時刻的8個預測電流為

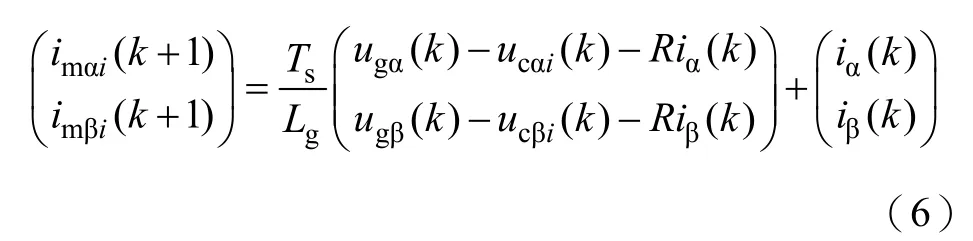
將式（6）代入式（3）可得

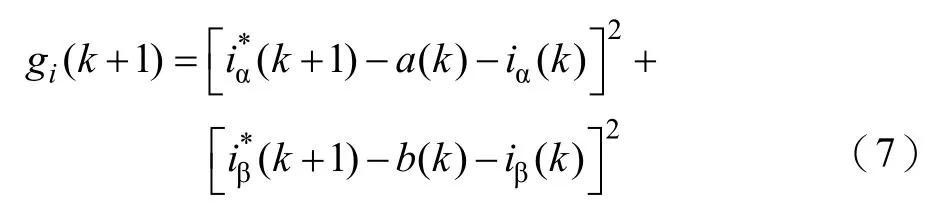
其中

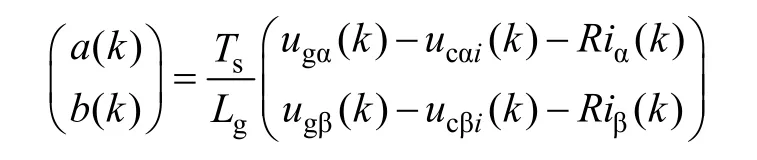
聯立式（7）和式（5）可得

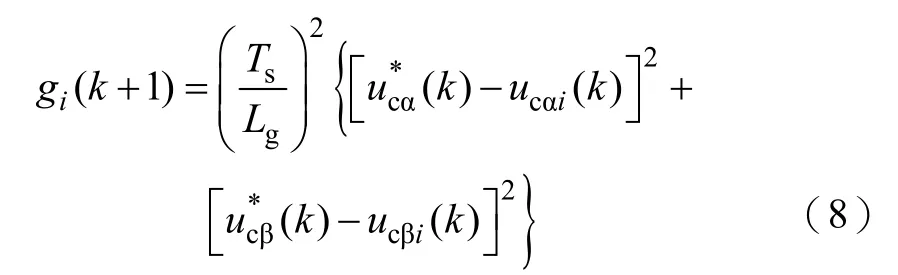
由式（8）可知，模型電流預測控制中的價值函數可由電壓預測值和8個輸入電壓表示。即根據式（8）可得到最優輸入電壓為與電壓預測值最相近的輸入電壓。將最優輸入電壓對應的開關狀態作為控制器的輸出可實現對 VSR系統的模型電壓預測控制。值得注意的是，式（8）所示的價值函數，其最小化的目的是為了得到與所需要的電壓矢量距離最近的電壓矢量，因此，可根據模型預測控制原理和空間電壓矢量的分布規律對最優輸入電壓進行選擇。

根據電壓矢量平面各點與8個電壓矢量的距離關系，將電壓矢量空間分為7個區域，如圖3所示。

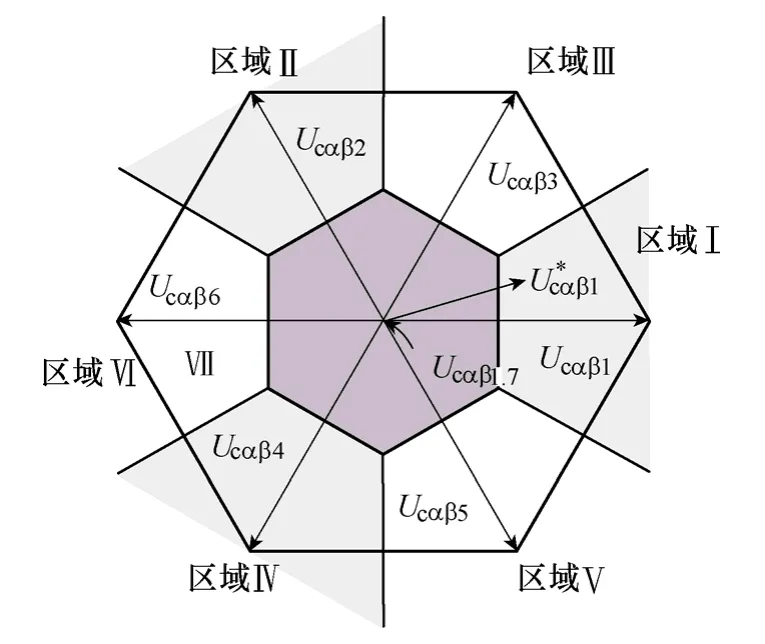
圖3 電壓矢量分區Fig.3 The section division of the voltage vector

為了判斷電壓矢量所在區域，可借鑒 SVPWM調制中采用的方法，定義變量

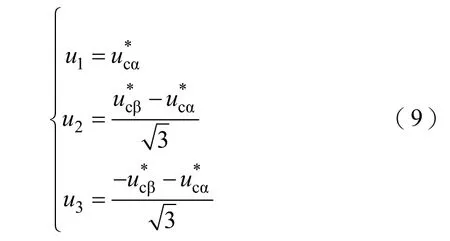
定義以下規則:若10u＞ ，則A=1，否則A=0；若20u＞ ，則B=1，否則B=0；若30u＞ ，則C=1，否則C=0。則電壓矢量所在區域的計算公式為

式（10）的區域計算結果N與圖3定義的區域號Ⅰ～Ⅵ對應。

在確定電壓矢量參考值所在區域N后，可進一步判斷電壓矢量參考值是否在區域Ⅶ所示的中間小六邊形范圍內，判斷方法為

通過以上分析可知，所提模型電壓預測控制可根據模型預測控制原理，通過對輸入電壓進行預測，并采用分區判斷的方法得到最優的電壓矢量，其控制框圖如圖4所示。

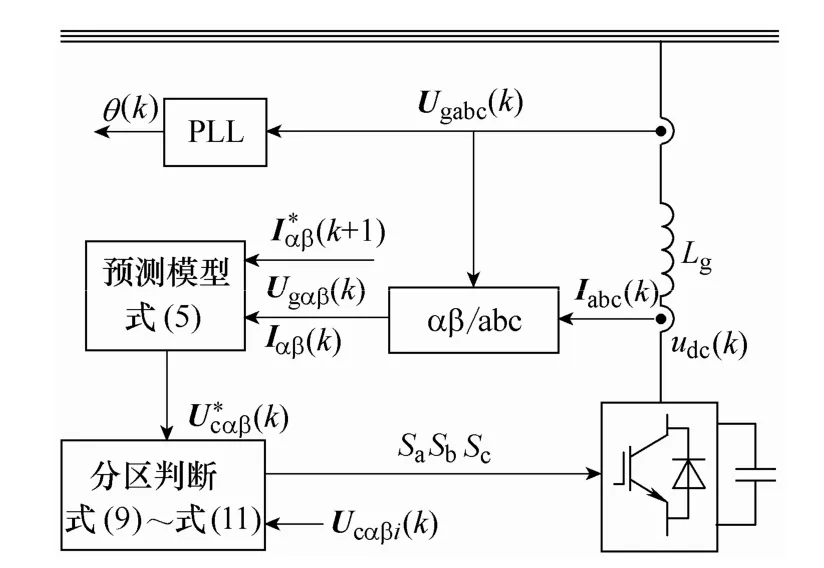
圖4 模型電壓預測控制框圖Fig.4 Block diagram of the MPC scheme

由圖4可以看出，采用兩相靜止坐標系下的電網電壓Ugαβ(k)、電流Iαβ(k)信號和k+1 時刻的參考電流值，通過VSR預測模型預測到跟蹤參考電流所需的電壓(k)；對電壓(k)所在分區進行判斷得到最優的電壓矢量作為控制器輸出。電流控制算法在每個控制周期需要進行 1次預測、4次乘法運算、3次加法運算、3次判斷和1次比較即可求出最優的電壓矢量，與模型電流預測控制相比，計算時間得到顯著縮短。

3 實驗分析

為驗證理論分析的正確性和有效性，構建了一套功率為1.0kW的VSR實驗平臺。系統采用TI公司的TMS320F28335作為核心控制器，實驗系統各參數見表。

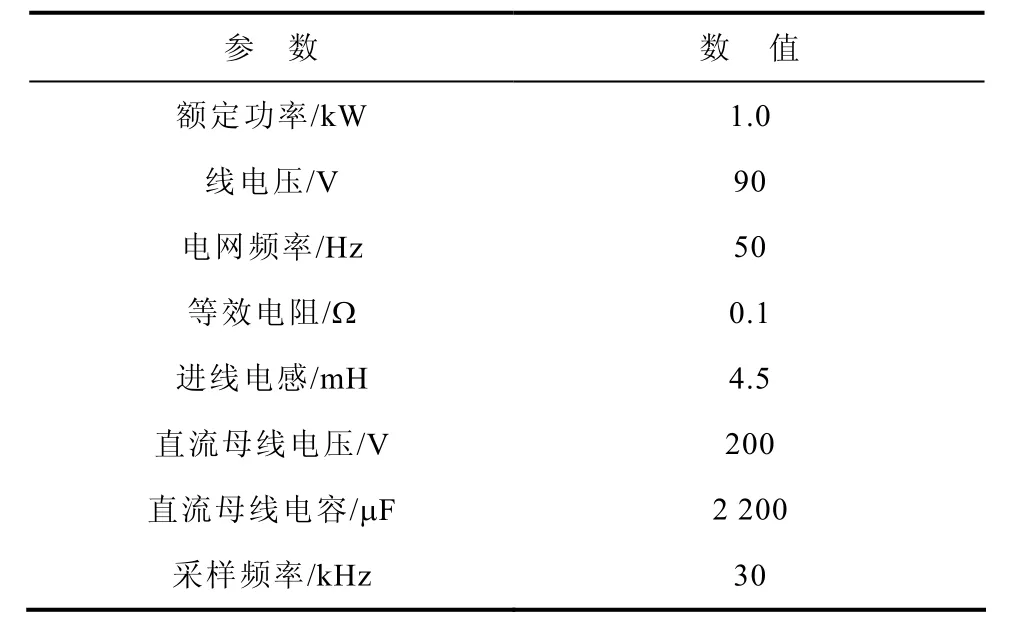
表 VSR系統參數Tab. VSR parameters

首先比較模型電流預測控制算法和模型電壓預測控制算法的計算耗時，如圖5所示。

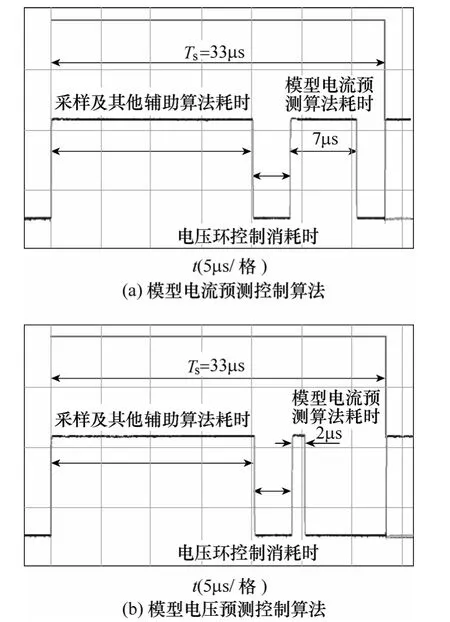
圖5 兩種算法的耗時比較Fig.5 Time dependencies for the two kind of algorithms

由圖 5a所示模型電流預測控制算法的計算耗時可以看出，整個算法耗時約30.5μs，其中，模型電流預測算法部分運行過程需要7μs；而圖5b的模型電壓預測控制算法中，預測控制算法部分運行過程僅為 2μs，約為模型電流預測控制算法耗時的28.6%。與模型電流預測算法相比，所提模型電壓預測算法結構較為簡單，可顯著縮短程序運行耗時。

為了驗證模型電壓預測控制的性能，分別對模型電流預測控制和模型電壓預測控制的動態電流響應過程進行比較，結果如圖6所示。

圖6 電流響應實驗波形Fig.6 Experimental waveforms of currents

由圖6a和圖6b可知，采用模型電流預測控制時，電流能夠快速跟蹤參考值，其響應時間約為0.2ms；由圖6c和圖6d可知，模型電壓預測控制的電流響應時間約為 0.2ms，同樣具有較快的電流響應速度，因此，所提模型電壓預測控制保持了模型電流預測控制的快速電流響應特性，具有較好的控制品質。

圖7a和圖7b分別為模型電壓預測控制算法的穩態電流波形和A相電流頻譜。

由圖7a可以看出，系統輸入電流穩定、波形正弦度較好、可實現單位功率因數運行。圖7b所示的電流頻譜分析顯示，A相電流總諧波含量為3.01%，電流諧波含量較低，控制效果優良。

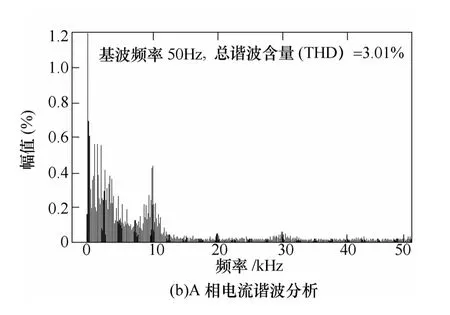
圖7 模型電壓預測控制穩態電流波形及電流諧波分析Fig.7 Steady state current waveforms and current harmonic analysis for model voltage predictive control

圖8為采用模型電壓預測控制的VSR系統在α軸電流參考值階躍變化時的三相電流波形。

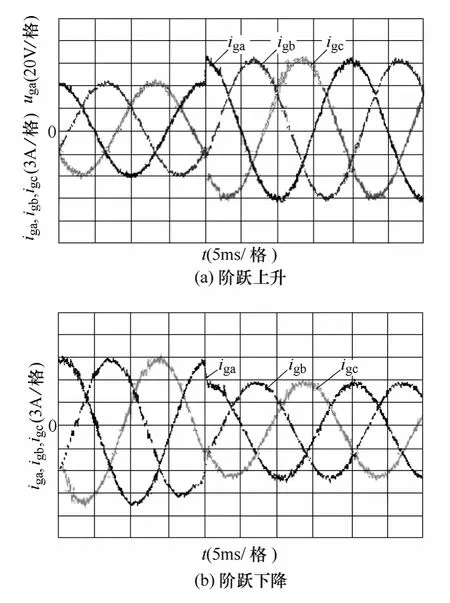
圖8 采用模型電壓預測控制時的電流波形Fig.8 Current waveforms for proposed algorithm

圖8a中，α軸電流參考值由峰值6A階躍上升到峰值9A；圖8b中α軸電流參考值由峰值9A階躍下降到峰值6A。電流階躍時間約為0.2ms，響應速度較快。

圖9為采用模型電壓預測控制的VSR系統在α軸電流參考值階躍變化時的電流矢量軌跡圖。

由圖9可以看出，VSR系統的輸入電流矢量軌跡為較標準的圓形，且電流階躍暫態過程很短。因此電流控制效果良好，具有較快的響應速度。

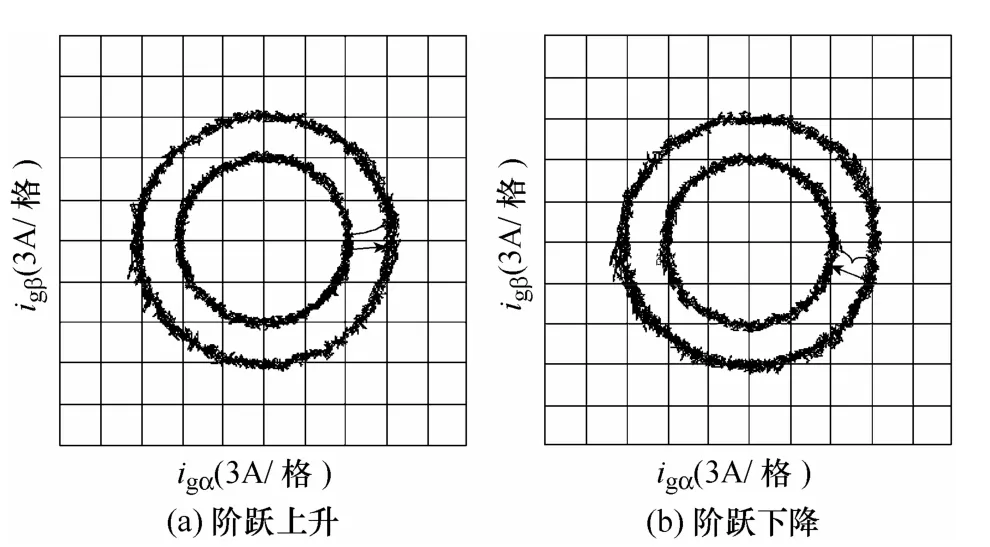
圖9 參考電流變化時的電流矢量軌跡Fig.9 Experimental current vector locus diagrams of dynamic response tests

4 結論

針對模型電流預測控制算法計算復雜、耗時較長的問題，提出了一種模型電壓預測控制算法。分析了模型電流預測控制的計算過程和運算量，采用電壓預測及電壓矢量分區判斷的方法快速選取最優電壓矢量作為控制器的輸出。實驗結果表明，所提模型電壓預測控制可以在保證模型電流預測控制電流響應速度快、控制效果好等優良品質的基礎上，有效簡化模型電流預測控制的計算過程，縮短算法執行時間，為輔助算法的加入及模型預測控制的工業化應用提供了有利條件。

[1] Xia C L, Wang M, Song Z F, et al. Robust model predictive current control of three-phase voltage source PWM rectifier with online disturbance observation[J]. IEEE Transactions on Industrial Informatics, 2012, 8(3): 459-471.

[2] Preindl M, Schaltz E. Sensorless model predictive direct current control using novel second-order PLL observer for PMSM drive systems[J]. IEEE Transactions on Industrial Electronics, 2011, 58(9):4087-4095.

[3] 楊勇, 趙方平, 阮毅, 等. 三相并網逆變器模型電流預測控制技術[J]. 電工技術學報, 2011, 26(6):153-159.

Yang Yong, Zhao Fangping, Ruan Yi, et al. Model current predictive control for three-phase grid-connected inverters[J]. Transactions of China Electrotechnical Society, 2011, 26(6): 153-159.

[4] 王宏佳, 徐殿國, 楊明. 永磁同步電機改進無差拍電流預測控制[J]. 電工技術學報, 2011, 26(6):39-45.

Wang Hongjia, Xu Dianguo, Yang Ming．Improved deadbeat predictive current control strategy of permanent magnet motor drives[J]. Transactions of China Electrotechnical Society, 2011, 26(6): 39-45.

[5] Geyer T, Papafotiou G. Model predictive direct torque control—Part I: Concept, algorithm and analysis[J].IEEE Transactions on Industrial Electronics, 2009,56(6): 1894-1905.

[6] 沈坤, 章兢, 王堅. 基于預測控制的三相電壓型逆變器并聯系統[J]. 電工技術學報, 2012, 27(12):63-70.

Shen Kun, Zhang Jing, Wang Jian. Three-phase voltage source inverters parallel system based on predictive control[J]. Transactions of China Electrotechnical Society, 2012, 27(12): 63-70.

[7] Perez M A, Rodriguez J, Fuentes E J, et al. Predictive control of AC-AC modular multilevel converters[J].IEEE Transactions on Industrial Electronics, 2012,59(7): 2832-2839.

[8] Quevedo D E, Aguilera R P, Perez M A, et al. Model predictive control of an AFE rectifier with dynamic references[J]. IEEE Transactions on Power Electronics,2012, 27(7): 3128-3136.

[9] Preindl M, Schaltz E, Th?gersen P. Switching frequency reduction using model predictive direct current control for high-power voltage source inverters[J]. IEEE Transactions on Industrial Electronics,2011, 58(7): 2826-2835.

[10] Vargas R, Cortes P, Ammann U, et al. Predictive control of a three-phase neutral-point-clamped inverter[J].IEEE Transactions on Industrial Electronics, 2007,54(5): 2697-2705.

[11] Kouro S, Cortes P, Vargas R, et al. Model predictive control—a simple and powerful method to control power converters[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 1826-1838.

[12] Geyer T. Computationally efficient model predictive direct torque control[J]. IEEE Transactions on Industrial Electronics, 2011, 26(10): 2804-2816.

[13] Zhang Y L, Lin Hua. Simplified model predictive current control method of voltage-source inverter[C].IEEE 8th International Conference on Power Electronics and ECCE Asia, 2011: 1726-1733.

[14] Cortes P, Wilson A, Kouro S, et al. Model predictive control of multilevel cascaded H-bridge inverters[J].IEEE Transactions on Industrial Electronics, 2010,57(8): 2691-2699.

[15] 王萌, 夏長亮,宋戰鋒,等. 不平衡電網電壓條件下PWM 整流器功率諧振補償控制策略[J]. 中國電機工程學報, 2012, 32(21): 46-53.

Wang Meng, Xia Changliang, Song Zhanfeng, et al.A power resonance compensation control strategy for PWM rectifiers under unbalanced grid voltage conditions[J]. Proceedings of the CSEE, 2012, 32(21):46-53.