基于切換模型的雙向AC-DC變換器控制策略

田崇翼 李 珂 張承慧 莊飛飛 葉保森

（山東大學控制科學與工程學院 濟南 250061）

0 引言

在能源需求和環境保護的雙重壓力下，分布式發電技術獲得了越來越多的重視和應用，微電網技術作為分布式電源和電網連接的橋梁和緩沖也成為當前的研究熱點[1,2]。目前常用的微網結構有交流微網、直流微網和交直流混合微網[3-6]。

在交直流混合微電網中，通常需要雙向AC-DC變換器作為能量接口單元，控制直流和交流母線功率流動，以保證微網功率平衡、維持母線電壓穩定并提高系統電能質量。目前多數研究交直流混合微電網的控制文獻都采用小信號建模方法來分析雙向AD-DC變換器[7-9]，基于狀態空間平均的小信號法簡單易用，便于穩定性分析以及控制器的設計。然而，交直流微網中含有大量波動性很強的微源，雙向 AC-DC變換器工作點需要大范圍的突變。小信號平均模型是通過忽略模型中高次項而近似得到，這種近似得到變換器小信號模型的建模方法存在大信號擾動時，系統可能出現不穩定、建模精度不高等諸多問題[10]。近年來，混雜系統理論和應用的不斷進步為電力電子系統建模和控制提供了一種新的工具。文獻[11]給出了切換線性自治系統穩定控制條件，提出通過設計切換序列使系統狀態趨近于一個穩定切換平衡點。文獻[12]進一步研究線性切換系統穩定切換律的設計問題，并以三種典型的DC-DC變換器進行了實際控制。文獻[13]以雙向DC-DC變換器為例研究了切換系統的能控性和能觀性，文獻[14]基于切換理論研究了三相PWM整流器在周期性切換律下的穩定性問題。文獻[15,16]研究了切換模型下的APF控制并取得很好的效果。文獻[17]探討了基于切換理論下開關變換器統一建模問題。采用電力電子混雜系統建模可以直接對系統大信號過程建模，不存在任何近似，得到模型較為精確，因此更能真實反映電力電子系統的實際物理工作過程。

本文基于切換系統理論，首先建立雙向AC-DC切換動態模型，然后采用儲能函數作為系統Lyapunov函數，以系統能量衰減最快為目標設計了最優切換控制策略。同時為了便于控制器數字化實現，建立了切換系統單步預測模型并對控制策略進行離散化處理。由于直接對系統大信號過程進行建模，本文所得到的模型比較精確，增強了雙向AC-DC變換器抗大范圍擾動的能力。相對于傳統的SVPWM調制方法，該算法無需進行矢量計算，對復雜電路的建模和分析更方便。本文最后進行了仿真模擬并搭建了實驗平臺，仿真和實驗結果表明所采用的建模方法和控制策略有效。

1 雙向AC-DC變換器切換系統模型

1.1 切換系統理論基礎

切換系統是一類重要的混雜系統[18]，它是由幾個連續時間子系統或離散時間子系統及作用在其中的切換規則構成的統一動態系統。在切換過程中，每一時刻系統的狀態只符合其中1個子系統的規律。通過在多個子系統之間進行適當切換，以實現一定的性能要求。切換信號可根據時間、狀態或由更復雜的方式產生。一般切換系統模型可以表示為

式中，σ(t,x)∶[0,∞]→{1, 2, …,m}為分段常值函數，右連續，稱為系統切換信號，對于由開關管組成的電力電子電路來說，m=2l，l為開關管對數。σ=k時表示系統處于第k個子系統。x為系統的狀態變量；u為系統輸入。電力電子電路中，每一種開關組合分別對應一種電路拓撲，由此可以得到相應子系統的連續狀態方程，不同開關組合的變化可以看作是離散事件，因此可以把變換器的實際工作過程描述為在特定切換規則的控制下不同連續子系統之間的切換。

1.2 雙向AC-DC切換建模

雙向AC-DC結構如圖1所示，其中，Ea、Eb、Ec為交流側三相電壓；ia、ib、ic為交流側三相電流；Udc為直流側電壓。R、L分別為濾波電抗器的電阻和電感；Ura、Urb、Urc為輸入整流器的三相離散電壓信號；C為濾波電容；kp(p=a, b, c) 表征開關器件狀態，定義kp=1表示第p對開關上橋壁開通，下橋壁關斷，k=0表示下橋壁開通，上橋壁關斷。

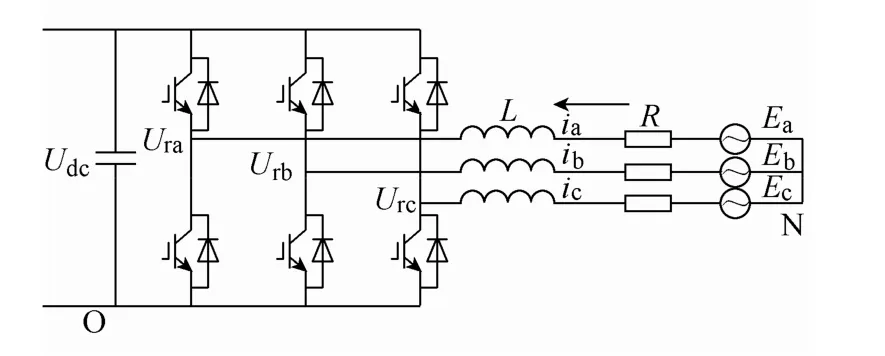
圖1 雙向AC-DC變換器結構圖Fig.1 Principle of AC-DC converter

根據基爾霍夫電壓定律，可以求出雙向AC-DC變換器電流電壓動態方程

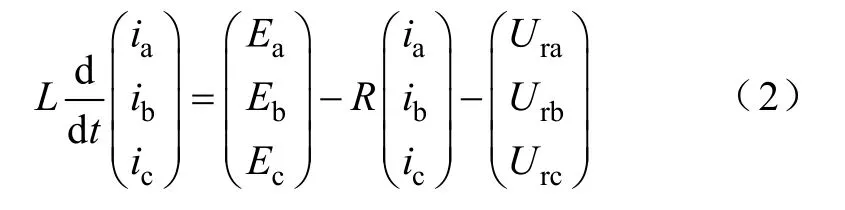
式中

雙向AC-DC變換器正常工作過程中，ka、kb、kc共對應8種有效開關組合，即:000、001、010、011、100、101、110、111。其中000和111組合作用相同，因此定義7種有效的切換模態，即σ(x)∈{1,2, ··, 7}，則系統開關函數可以表示為

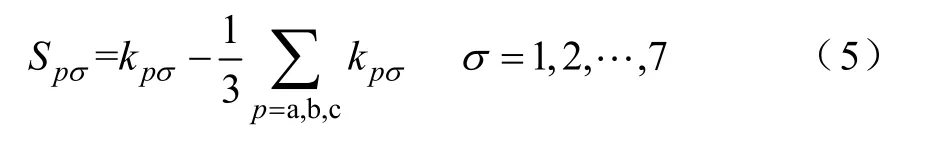
式中，pSσ表示第p對開關在切換到σ模式時的值，引入狀態變量x=(ia, ib, ic)T，針對每一種開關組合，可以得到一種電路拓撲和相應的狀態方程。假定三相交流電壓對稱，并忽略三相交流線路電阻電感的不對稱性，得到雙向AD-DC變換器切換模型為

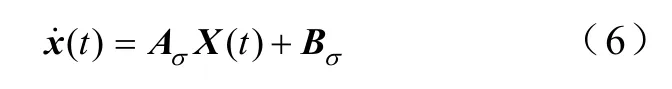
其中

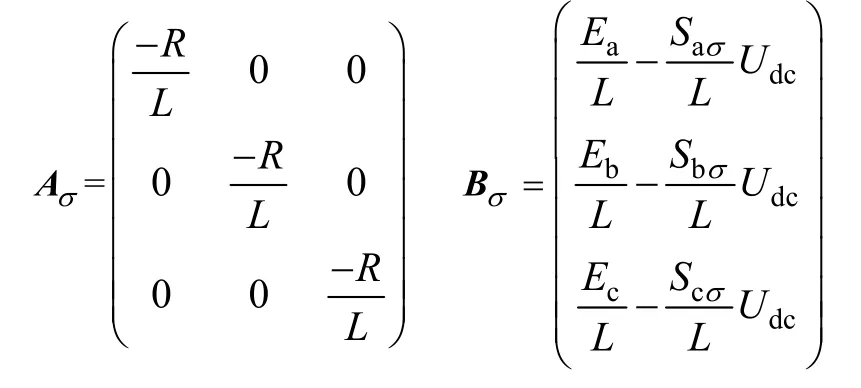
2 最優切換路徑設計

雙向AC-DC的電流跟蹤控制目標是使得系統狀態滿足x(t)=x*,x*為外部給定的參考值，可以視為系統的切換平衡點。由式（6）可知，通過控制σ(x)選擇不同值，就可以得到對應的電力電子器件驅動信號，從而使得AC-DC變換器切換到不同的狀態方程。因此需要設計系統的最優切換規則，從而在保證系統全局穩定的前提下，控制狀態變量的運動軌跡使之盡快收斂于切換平衡點。

2.1 最優切換律設計

引理1如果切換系統的所有子系統具有共同的Lyapunov函數V(x)，其中V(0)=0，并滿足

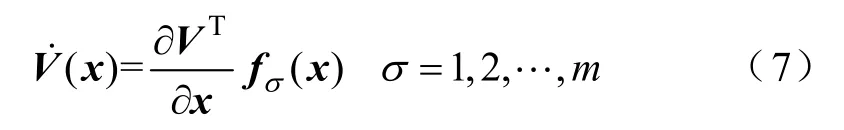
則切換系統在任意切換路徑漸近穩定。

對于雙向AC-DC而言，由于其含有儲能元件，所以本文選擇其儲能函數作為共同Lyapunov函數，設F=diag{L, L, L}，則有共同Lyapunov函數

設計切換律

如果能夠證明在該切換律下，切換系統整個運行區間都能夠保證，則表示切換系統將能夠收斂于期望的切換平衡點，而且收斂速度最快。

證明:設τ 為滿足的所有向量集合，定義切換系統各個子系統凸組合為

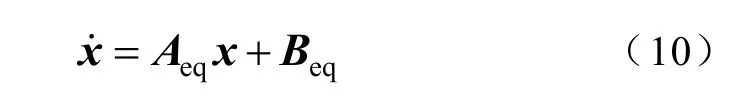
令ζ=x-x*，式（10）可以變化為

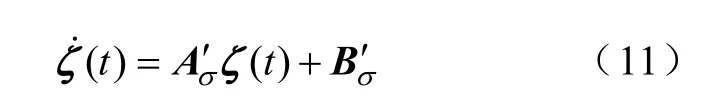
式中

切換系統共同Lyapunov函數的導數可以表示為

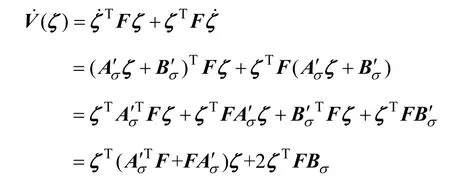
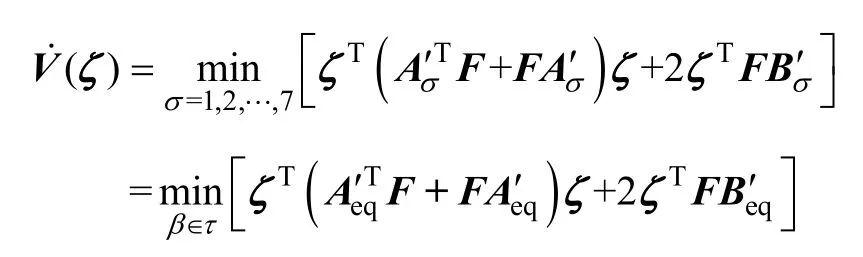
由 AC-DC切換系統模型可知，無論β如何取值，始終有=d iag ｛ - 2R, - 2R, - 2R｝＜0。

將x*=(i*a, i*b, i*c)T代入式（11）得

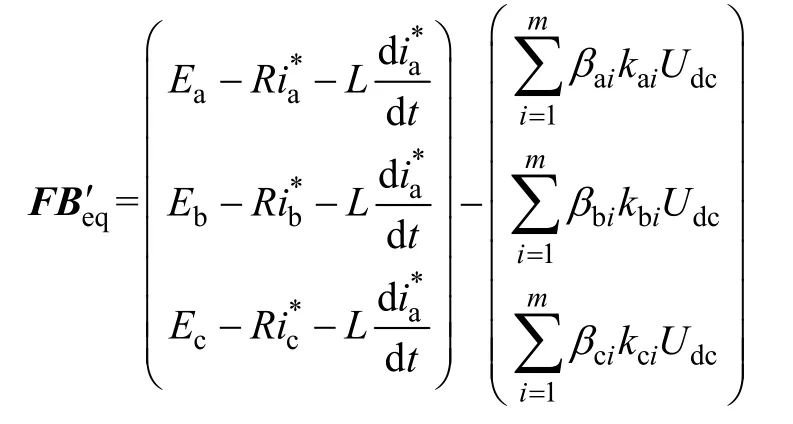
根據雙向 AC-DC電路的物理特性可知，正常工作時，雙向AC-DC直流側電壓Udc大于其交流側電壓Ep(p=a, b, c)減去線路阻抗上的壓降(電阻和電感上的壓降)，因此存在一組βi(0＜βi＜1)，使得FBeq≤0，從而可以得到min[2ζTFBeq]≤0。

2.2 基于單步預測的切換律離散化

設 AC-DC變換器采用固定周期采樣，采樣周期為ΔT，設采樣周期開始時雙向 AC-DC變換器狀態為X(t)，AC-DC每次都在下一個采樣周期更新開關管的控制型號，當采樣周期ΔT足夠小時，有

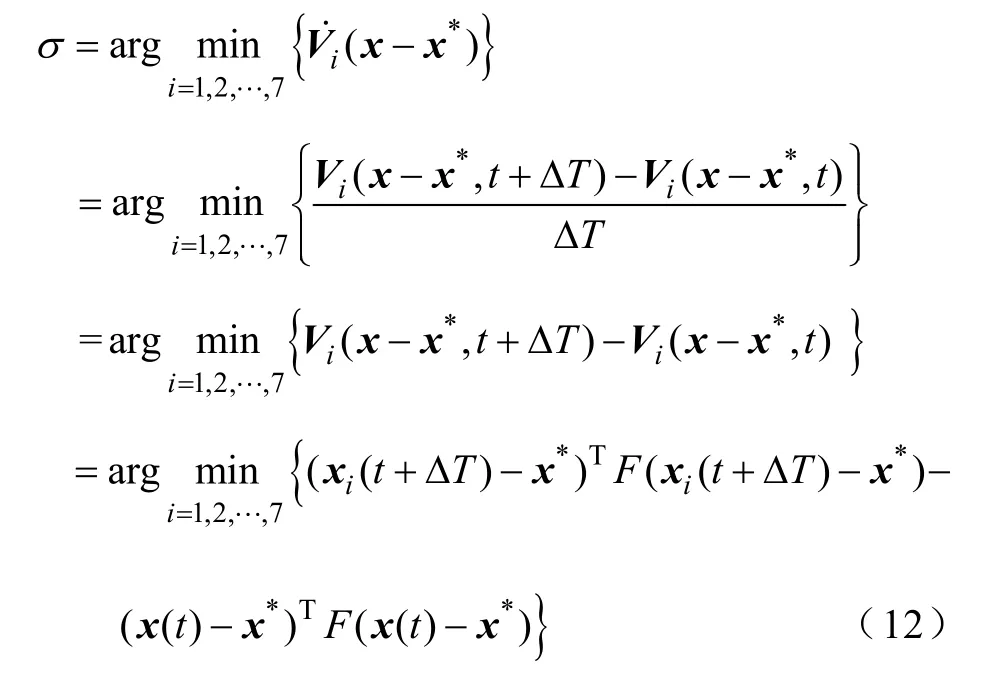
式中，x(t)為t時刻的實時采樣值，x*為給定，因此公式的后一項為確定數值，對σ的選擇沒有影響，上式可以進一步簡化為

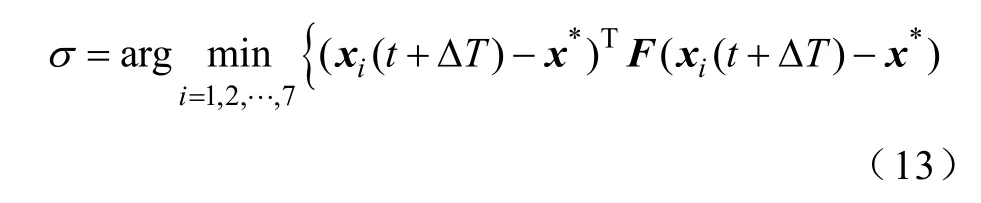
對線性系統狀態方程進行求解，可以得到

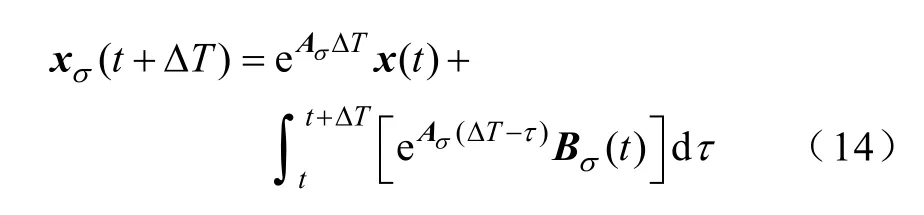
考慮到實際工作中，AC-DC系統采樣速度很快，可以認為在一個采樣周期內U(t)、E(t)均保持不變，為了方便數字處理器運算，用狀態變量的商差代替微商對上式進行離散化

綜上，最優切換律的物理意義可以由圖2所示。當切換系統選擇不同的切換路徑時，經過一個采樣周期后得到的不同的狀態變量xi(t+ΔT)，各xi(t+ΔT)和期望的狀態點x*的距離Ji也不相同，最優切換律實際上選擇了一個離x*最短距離的模態為下一個周期的控制信號，從而保證系統收斂最快。

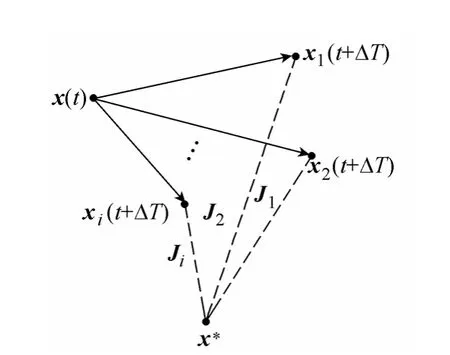
圖2 最優切換控制序列物理意義Fig.2 Principle of optimal switching path

3 交直流混合微電網中雙向AC-DC的控制策略

在交直流混合微網、電池儲能等多數場合中，雙向AC-DC變流器被用來控制系統交流側和直流側間的能量流動，以保證交直流側能量平衡，維持直流母線電壓恒定。為此采用電壓電流雙閉環控制策略，控制策略如圖3所示。其中電壓外環采用PI控制，以直流母線電壓穩定為控制目標。為了防止電壓擾動造成頻繁切換，采用了滯環給定方式，和分別為整流和逆變過程電壓給定。整流和逆變分別采用正向和負向電壓調節器，二者輸出限幅后相加作為電流內環的給定，＞0時系統工作于整流狀態，雙向變換器從交流側傳遞能量到直流母線；＜0時工作于逆變狀態。為保證系統工作在單功率因數狀態時，將設置為0。

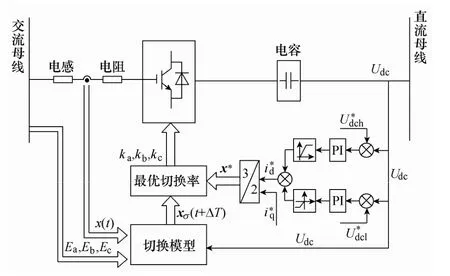
圖3 雙向AC-DC變換器控制策略圖Fig.3 Block diagram of control of bi-directional AC-DC converter

4 仿真分析與實驗驗證

4.1 仿真分析

在Matlab/Simulink 環境下搭建仿真模型，雙向AC-DC參數如下:濾波電感L=7mH；線路阻抗R=2，采樣周期ΔT=100μs；直流母線電容C=470μF；電壓外環PI調節器比例常數Kp=0.8，積分常數Ki=0.2；整流和逆變運行時的Udc分別為685V和700V；電網電壓為380V/50Hz。

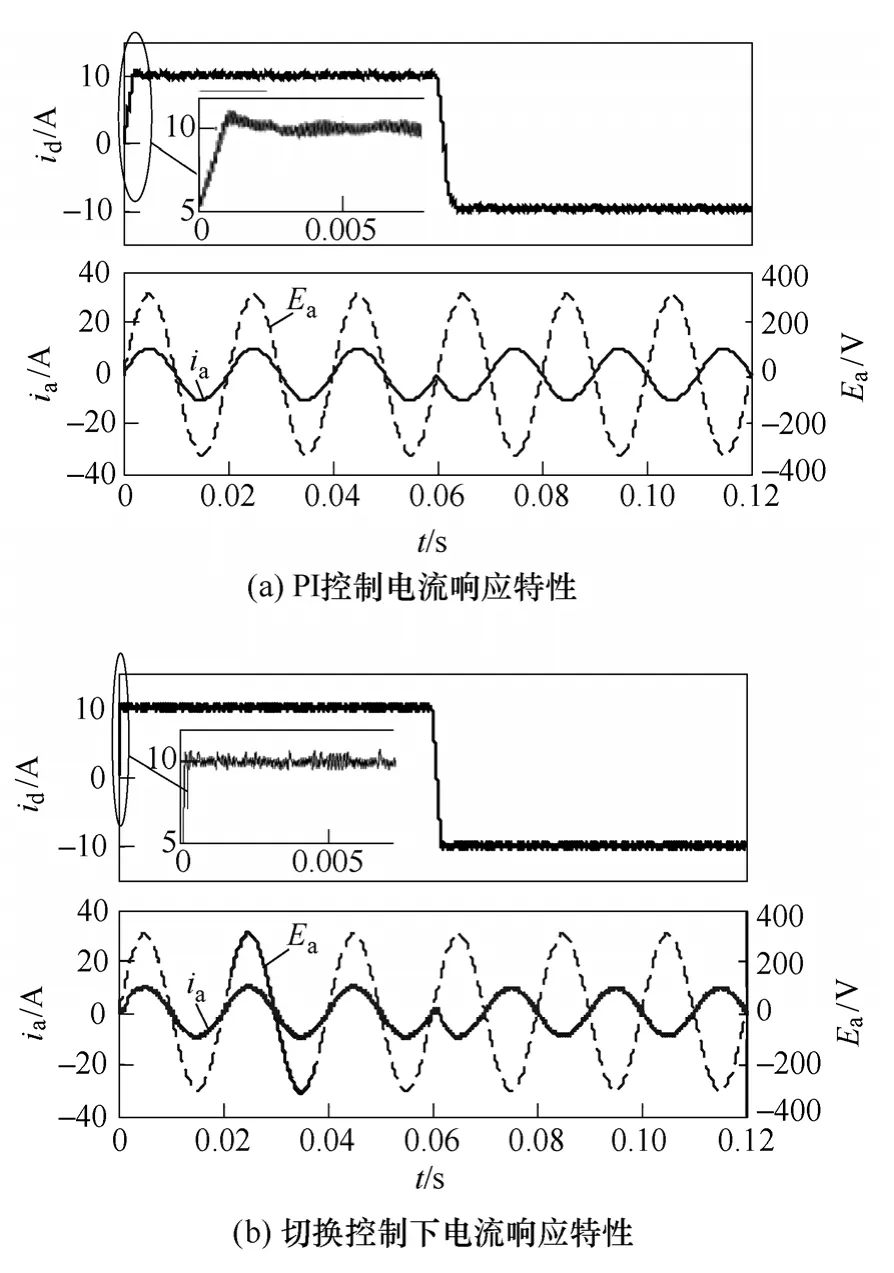
圖4 電流環仿真結果Fig.4 Current loop simulation results

圖5是模擬微網功率流動變化過程的雙閉環控制的仿真結果，仿真過程中對直流母線突加突卸2kW負載，雙向變換器由1kW逆變→1kW整流→1kW逆變。由圖5可知，負載切換過程中直流母線電壓能夠在約0.01s內穩定，電壓波動幅值最大不超過7%，仿真結果表明，本文控制策略能夠有效控制微網中交流和直流間的功率流動，維持電壓穩定。

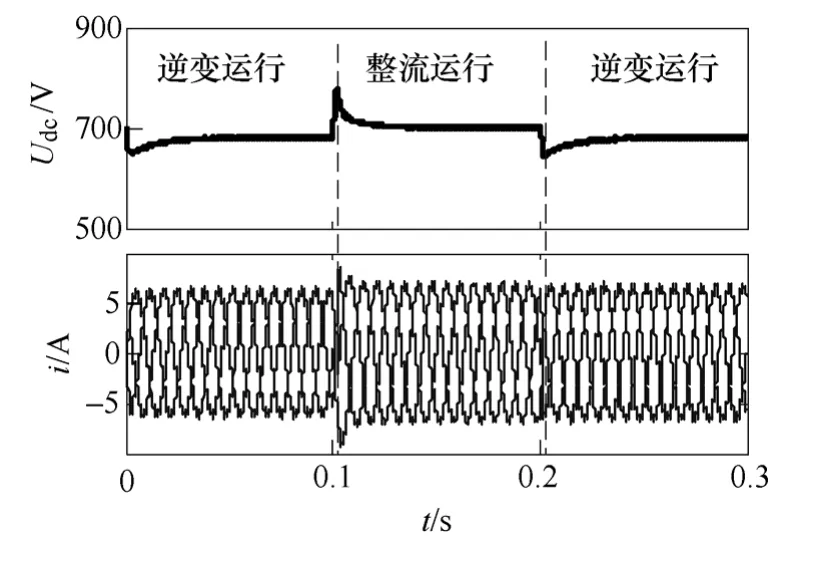
圖5 雙閉環仿真結果Fig.5 Double-loop simulation results

4.2 實驗驗證

采用與仿真相同的參數，在實驗室搭建了AC-DC雙向變換器實驗系統，其中主控制器采用dsPACE MicroautoboxII-1401，采用Chroma-62150H-1000S可編程電源模擬可再生能源向直流母線提供功率，電阻箱用來模擬用電負載。設置系統采樣周期ΔT=100μs，開關死區Td=3μs。

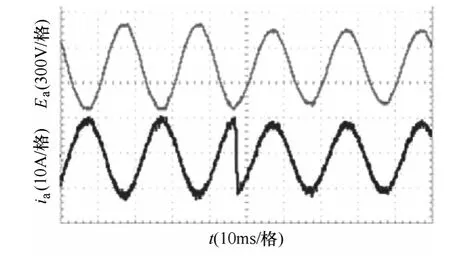
圖6 電流環實驗結果Fig.6 Experimental waveforms of current loop control

雙閉環實驗結果如圖7所示，其中圖7a是變換器由逆變切換整流過程中a相電壓電流波形和直流母線電壓變化圖。其中圖7b是變換器由整流切換逆變過程中a相電壓電流波形和直流母線電壓變化圖。由實驗結果可知，雙向AC-DC工作過程中電流正弦度良好，且可以實現整流和逆變之間的平滑無縫切換。

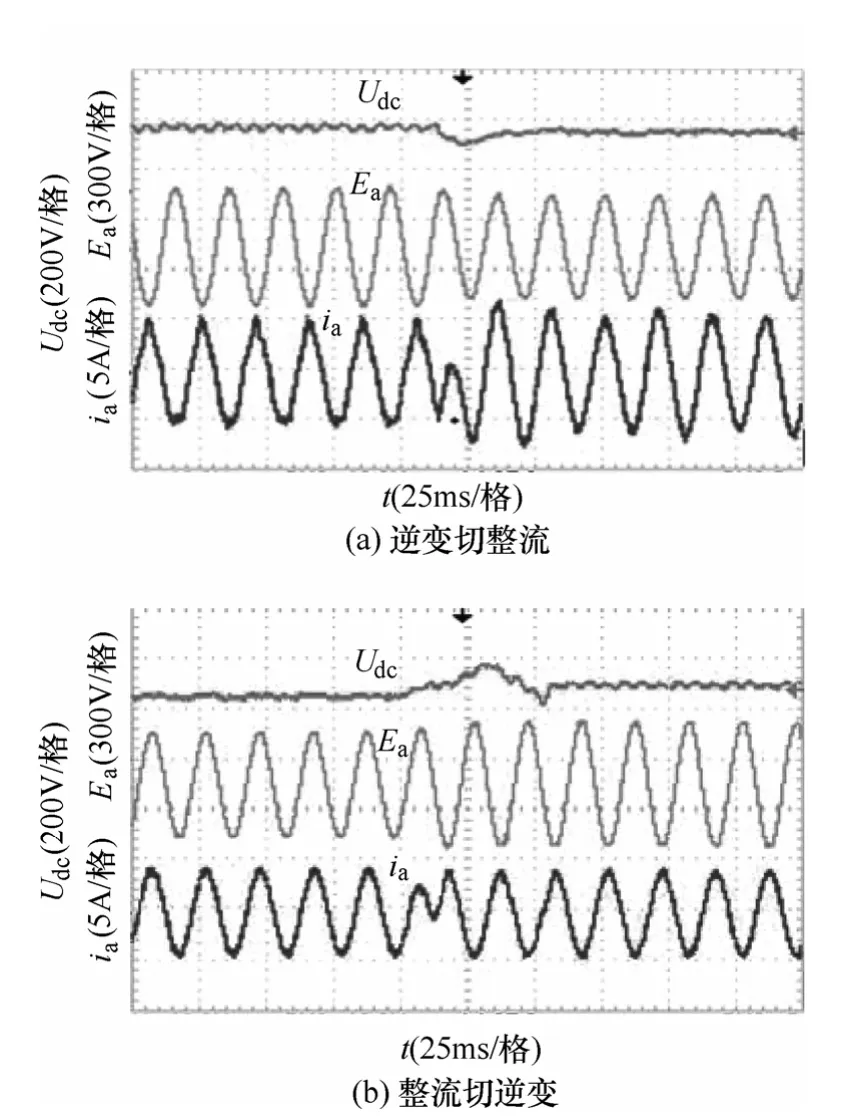
圖7 雙閉環實驗結果Fig.7 Experimental waveforms of double closed-loop control

5 結論

本文基于切換理論建立了雙向AC-DC變換器的切換動態模型，以系統儲能函數能量收斂最快為目標設計了最優切換序列控制算法，并證明了其穩定性。通過切換系統單步預測模型對切換律進行離散化。仿真和實驗結果表明系統靜態和動態控制效果都較好；驗證了模型的正確性以及控制策略的有效性。

相對于傳統的平均狀態建模方法，切換系統理論建模更利于描述電力電子電路的變結構行為，而且通過設計切換路徑完成開關管控制，不需要任何PWM調制策略，原理簡單、實現容易。

[1] Marnay C, Robio F J, Siddiqui A S. Shape of the micro-grid[C]. IEEE Power Engineering Society Winter Meeting, Columbus, OH, USA, 2001, 1:150-153.

[2] 王成山, 李鵬. 分布式發電、微網、智能配電網的發展與挑戰[J]. 電力系統自動化, 2010, 34(2):10-14.

Wang Chengshan, Li Peng, Development and challenges distribution generation, the micro-gird and smart distribution system[J]. Automation of Electric Power Systems, 2010, 34(2): 10-14.

[3] Lasseter R H, Akhil A, Marnay C, et al. White paper on integration of distributed energy resources, the certs microgrid concept[C]. Consortium for Electric Reliability Technology Solutions, 2002: 1-27.

[4] Barnes M, Ventakaramanan G, Kondoh J, et al. Real world micro-grids—an overview[C]. IEEE International Conference on System of Systems Engineering, San Antonio, TX, USA, 2007: 1-8.

[5] 吳衛民, 何遠彬, 耿攀, 等. 直流微網研究中的關鍵技術[J]. 電工技術學報, 2012, 27(1): 98-113.

Wu Weimin, He YuanBin, Geng Pan, et al. Key technologies for DC micro-grids[J]. Transactions of China Electrotechnical Society, 2012, 27(1): 98-113.

[6] Salehi V, Mohamed A, Mohammed O A. Implementation of real-time optimal power flow management system on hybrid AC/DC smart microgrid[C].Industry Applications Society Annual Meeting (IAS),2012 IEEE Digital Object Identifier, 2012: 1-8.

[7] Yukita K, Shimizu Y, Goto Y, et al. Study of AC/DC power supply system with DGs using parallel processing method[C]. Proceedings of IEEE International Power Electronics Conference, Sapporo,Japan, 2010.

[8] Liu X, Wang P M, Loh P C. A hybrid AC/DC microgridand its coordination control[J]. IEEE Transactions on Smart Grid, 2011, 2(2): 278-286.

[9] 張犁, 吳田進, 馮蘭蘭, 等. 模塊化雙向 AC/DC變換器并聯系統無縫切換控制[J]. 中國電機工程學報, 2012,32(6): 90-96.

Zhang Li, Wu Tianjin, Feng Lanlan, et al. Seamless switching control for modular bi-directional AC/DC converter parallel systems[J]. Proceedings of the CSEE, 2012, 32(6): 90-96.

[10] 馬皓, 祁峰, 張霓. 基于混雜系統的DC-DC變換器建模與控制[J]. 中國電機工程學報, 2007, 27(36):92-96.

Ma Hao, Qi Feng, Zhang Ni. Modeling and control for DC-DC converters based on hybrid system[J].Proceedings of the CSEE, 2007, 27(36): 92-96.

[11] Decarlo R A, Branicky M S, PetterssonS, et al.Perspective sand results on the stability and stabilizability of hybrid systems[J]. Proceedings of the IEEE, 2000, 88(7): 1069-1082.

[12] Deaecto G S, Geromel J C, Garcia F S, et al. Switched affine systems control design with application to DC-DC converters[J]. IET Control Theory and Applications, 2010, 4(7): 1201-1210.

[13] 胡宗波, 張波, 鄧衛華, 等. 基于切換線性系統理論的DC/DC 變換器控制系統的能控性和能達性[J].中國電機工程學報, 2004, 24(12): 165-170.

Hu Zongbo, Zhang Bo, Deng Weihua, et al.Controllability and reach ability of DC/DC converters as switched linear system[J].Proceedings of the CSEE,2004, 24(12): 165-170.

[14] 李瓊林, 劉會金, 宋曉凱, 等. 基于切換系統理論的三相變換器建模及其穩定性分析[J]. 電工技術學報, 2009, 24(11): 90-95.

Li Qionglin Liu Huijin Song Xiaokai, et al. Modeling and stability analysis of three-phase converter based on switching system theory[J]. Transactions of China Electrotechnical Society, 2009, 24(11): 90-95.

[15] 李春文, 湯洪海, 鄭雪生, 等. 三相 APF的切換系統建模與二次最優控制[J]. 中國電機工程學報,2008, 28(12): 66-72.

Li Chunwen, Tang Honghai, Zheng Xuesheng, et al.Modeling and quadratic optimal control of threephase apf based on switched system[J]. Proceedings of the CSEE, 2008, 28(12): 66-72.

[16] 郭曉云, 劉會金, 曹玉勝. 基于切換仿射線性模型的三相 APF電流控制方法[J]. 中國電機工程學報,2011, 31(4): 59-66.

Guo Xiaoyun, Liu Huijin, Cao Yusheng. A novel current control method for three-phase apf based on switched affine model[J]. Proceedings of the CSEE,2011, 31(4): 59-66.

[17] 李繼方, 韓金剛, 湯天浩. 基于切換系統的開關變換器統一建模[J]. 華南理工大學學報(自然科學版),2011, 39(10):157-163.

Ma Hao, Qi Feng, Zhang Ni. Unified modeling of switching converters based on switching system[J].Journal of South China University of Technology(Natural Science Edition), 2011, 39(10): 157-163.

[18] 程代展, 郭宇驀. 切換系統進展[J]. 控制理論與應用, 2005, 22(12): 954-960.

Cheng Daizhan, Guo Yuqian. Advances on switchedsystems[J]. Control Theory and Applications, 2005,22(12): 954-960.