采用區間控制的蓄電池儲能電站調峰運行控制策略

尚 瑨 邰能靈 劉 琦 陳 彬 陳金祥 惠 東

（1.上海交通大學電子信息與電氣工程學院 上海 200240 2.福建省電力試驗研究院系統所 福州 350003 3.中國電力科學研究院電工與新材料研究所 北京 100192）

0 引言

隨著國民經濟的快速發展，用戶對電力的需求不斷增加，電網的電力負荷峰谷差逐漸加大，運行中必須采取調峰措施，以保證電力系統供用電的平衡[1]。傳統的調峰方法一般有火電調峰[2,3]、燃氣輪機組調峰[4]和水電調峰[5,6]，這些方法都是從發電側進行調節，通過調整全網發電機的出力來跟隨電網負荷的波動。這對發電機組的調峰容量提出了較高的要求，而且機組的頻繁起停也造成了燃料資源的浪費。從建設成本和能源利用的角度出發，通過增加發輸配電設備來滿足高峰負荷的需求變得越來越困難。儲能電站可以從負荷側對電網的峰谷負荷進行調節，起到削峰填谷的雙向作用，不僅可以減少發電、輸電設備的投資，提高設備利用率，還可以減小線路損耗，獲得可觀的經濟效益，是解決電網峰谷差問題的有效途徑[7]。

在現有的儲能技術中，利用抽水蓄能電站實現電網削峰填谷的技術已經發展成熟并實用化。但由于受建設環境、地理位置的制約，有很大的局限性，難以得到大范圍的應用。蓄電池儲能電站（Battery Energy Storage System，BESS）具有儲能密度大、安裝建設靈活、可四象限平滑運行等優點，可以更方便地應用，有效平抑電網負荷的波動。目前關于蓄電池儲能電站在電力系統中應用的研究較多，但大多集中在改善電能質量[8,9]、平抑可再生能源波動[10]、提高新能源滲透率[11,12]等方面，對削峰填谷控制策略的研究較少。

文獻[13]建立了用于削峰填谷的電池模型。文獻[14]從減少輸電、配電損失方面探討了利用BESS進行削峰填谷的經濟意義。文獻[15]從用戶的角度出發，考慮電價差異安排蓄電池優化運行，減少了用戶電費支出。文獻[16]利用蓄電池儲存光伏電站發出的電能，在負荷高峰時放電，解決光伏發電高峰時段和負荷高峰時段不匹配的問題。以上研究對蓄電池儲能電站用于電網削峰填谷的針對性不強，沒有對控制策略進行系統的研究。文獻[17]對BESS用于削峰填谷的控制策略進行了探討，但所做分析同時包含電壓穩定和經濟效益等多個目標，并未對削峰填谷策略進行深入研究。

本文在短期負荷預測的基礎上，提出了一種基于區間控制的蓄電池儲能電站削峰填谷控制策略。考慮 BESS容量及每周期充放電量的均衡，設定負荷參考區間，并通過該區間來區分波峰、波谷。該策略計算簡單，實用性很強，采用變功率控制，可以靈活地適應負荷的變化。在此基礎上，針對預測負荷存在誤差的問題，初步提出一種簡單實用的調整策略，通過仿真分析驗證了所提策略的可行性。

1 基于負荷預測的BESS運行控制

在配電網中，普遍存在日負荷分布不均的情況，引入BESS來進行削峰填谷，可以有效提高供電質量。在圖1所示的配電網中，電網通過變壓器T向該區域供電。由于各母線上的負荷全天分布不均，導致流經變壓器T的總負荷PT存在較大峰谷差。在加入BESS之后，可以通過合理控制BESS運行模式，實現PT的相對穩定。

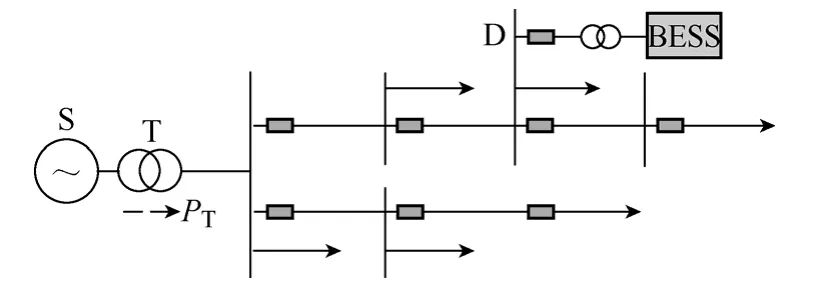
圖1 配電網示意圖Fig.1 Diagram of distribution system

1.1 定邊際負荷控制

對某一固定區域，結合歷史負荷曲線，并考慮天氣、特殊事件等因素，可以得到日負荷曲線的預測值。以圖 2所示負荷曲線為例，在不考慮 BESS容量約束的情況下，通過計算可以得到邊際負荷值Pd，當區域負荷小于該值時，使 BESS運行在充電狀態，消除波谷；而在負荷大于該值時，使 BESS運行在放電狀態，消除波峰。

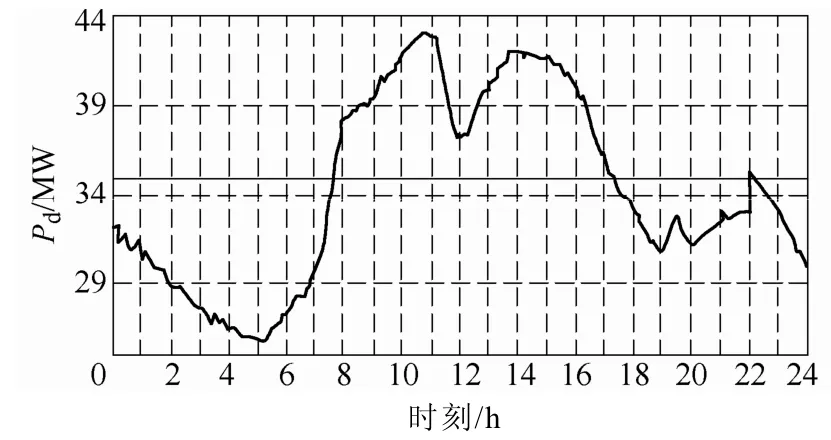
圖2 定邊際負荷示意圖Fig.2 Diagram of load threshold

對Pd的求取以BESS充放電量均衡為目標，可以建立等式

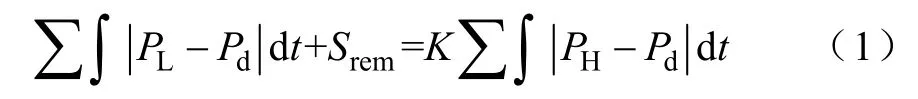
采用迭代法求取Pd，取區域日平均負荷P1作為初值進行迭代。令

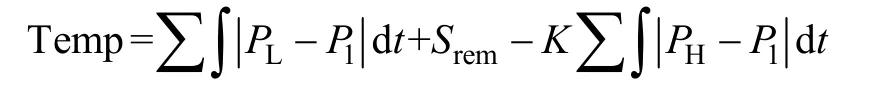
確定邊際負荷Pd之后，即可在預測的日負荷曲線基礎上確定BESS全天的運行模式，使負荷曲線平穩維持在Pd上下。

然而，這種控制方式僅從BESS全天充放電量均衡的角度出發，沒有考慮BESS實際容量的限制。實際上，由于投資、場地等因素的制約，BESS的容量是有限的。

1.2 負荷區間控制

在圖 2所示的定邊際負荷控制方案中，BESS在 0:00～7:30時段、18:00～21:30時段處于充電狀態；在7:30～18:00時段處于放電狀態。整體來看，全天充放電量達到了均衡，但每個獨立的充放電時段都較長，充放電量較大，這對BESS的容量提出了很高的要求。

對于既定的BESS，系統的容量有限，可以考慮設定一個日負荷波動區間，即將削峰填谷控制目標從原來的保證日負荷曲線嚴格在Pd周圍波動，降低為在一個區間內波動。

如圖3所示，(Pd1,Pd2)為設定的負荷波動區間，當負荷低于Pd2時，BESS充電；當負荷高于Pd1時，BESS向外放電。

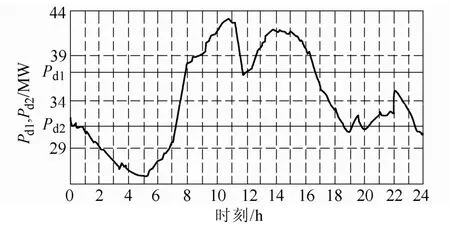
圖3 負荷區間示意圖Fig.3 Diagram of load interval

Pd1和Pd2的取值要兼顧全天充放電量的均衡，以及BESS的容量。因此需要滿足以下條件

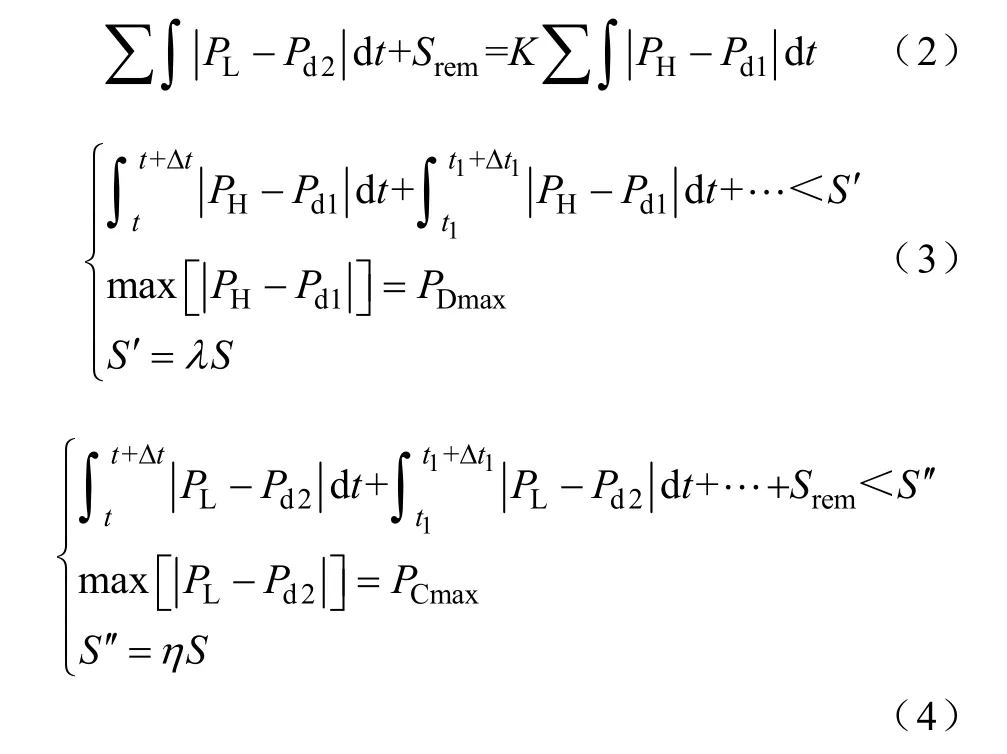
式中，S為BESS容量；λ為保證蓄電池不過放電的可靠性系數；η為保證蓄電池不過充電的可靠性系數；PCmax和PDmax分別為BESS最大充放電功率，在計算BESS充放電電量時，需要考慮BESS實際最大充放電能力。

通過以上約束條件，不僅可以保證BESS充放電量的均衡，同時可以保證充放電量均在BESS容量范圍之內。

由于對負荷PT的控制目標為一個區間，所以在實際運行中，BESS系統不會頻繁在充放電狀態之間切換。全天充電時段和放電時段分別集中在某個大的時間區間，基本可以認為負荷曲線由波谷段和波峰段組成（以圖3為例，負荷曲線在白天有兩個高峰，且中間沒有波谷，這兩個連續波峰組成了一個波峰段）。因此，對連續時段的充放電量進行考慮后，可以不具體考慮BESS上一時段電量狀態對下一時段充放電的限制。

對Pd1和Pd2的求取同樣采取迭代的方式。如圖3所示負荷曲線，通過上述迭代算法，可以求出邊際負荷值Pd。以Pd為中心，令Pd1=Pd+ΔP，Pd2=Pd?ΔP，作為Pd1和Pd2的初值進行迭代。

首先校驗Pd1和Pd2的取值是否可以保證充放電量均在BESS容量范圍之內，即是否滿足

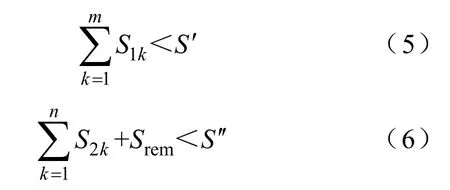
式中，S1k為每個放電時間段的放電量，m為全天BESS放電時段數量；S2k為每個充電時間段的充電量，n為全天BESS充電時段數量。若式（5）不滿足，則說明放電量大于BESS容量，即設定的放電邊際負荷Pd1太小，需要增大Pd1，令Pd1=Pd1+ΔP；同樣，若式（6）不滿足，則說明設定的充電邊際負荷Pd2太大，令Pd2=Pd2?ΔP，重新進行迭代校驗。直到滿足式（5）、式（6），取此時的Pd1和Pd2值作為初值進行下一輪校驗。

第二輪校驗以BESS充放電量均衡為目標，與上節中求取Pd的思路類似。取上一輪迭代得到的值Pd1和Pd2，令

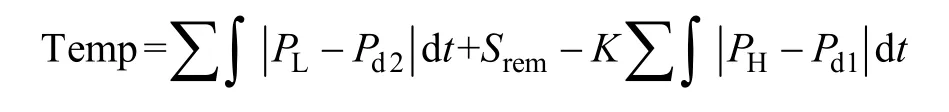
當Temp＜ε時，則認為迭代完成，當前Pd1和Pd2的值即為所求的邊際負荷值；當＞ε時，若Temp＞0則說明充電量大于放電量，在BESS容量約束下，只能選擇減小充電量，即將Pd2的值減小，令Pd2=Pd2?ΔP'，Pd1保持不變，重新進行迭代校驗；反之，若 Temp＜0，則令Pd1=Pd1?ΔP'，Pd2保持不變，重新進行迭代校驗，直到滿足＜ε。第二輪迭代變量ΔP'的取值應該相對較小，以使迭代計算更加精確。

以上迭代計算的流程圖如圖4所示，迭代計算的兩個階段用虛線隔開。

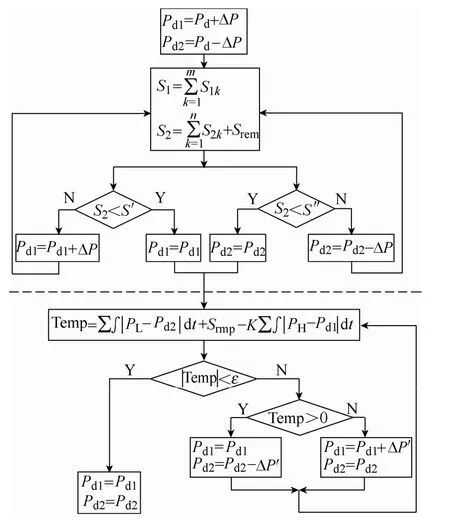
圖4 邊際負荷Pd1和Pd2迭代算法流程圖Fig.4 Flow chart of strikingPd1and Pd2

通過以上計算，可以初步得到蓄電池運行狀態的判斷區間，據此設定蓄電池在不同時段的充放電運行狀態。

然而對BESS來說，除了要考慮充放電運行狀態，還需要考慮充放電功率。

1.3 分時分檔功率確定

為了確定不同時段BESS與配電網交互功率的大小，可以用分時分檔匹配的方法來安排BESS具體充放電功率[10]。

首先，可以將全天24h均分為N個時段，每個時段對BESS運行狀態進行重新設定。而對于BESS，可以將充放電功率分檔。由于配電網負荷高峰對電能質量的影響大于負荷低谷，因此對BESS放電功率的設置比充電功率更加精細。如將充電倍率設置為0、0.2C、0.4C、…、1C；將放電倍率設置為0、0.1C、0.2C、…、1C。也可以根據實際負荷波動情況以及BESS的充放電特性，進行其他形式的充放電功率分檔。

在對 BESS充放電功率進行分檔匹配時，功率值會處于某一區間，而不是設定的充放電功率點上。在圖3中，9:00時，配電網負荷功率為，此時為負荷高峰，負荷缺額為，需要BESS向外放電，而'可能落在區間（0.1C,0.2C）內。因此，在選擇具體充放電功率時，需要進行統一規定，如向上或向下取值。

在實際運行中，配電網實時負荷與負荷預測會有一定出入。為了保證削峰填谷的效果，在選擇BESS充放電功率時，可以引入BESS剩余電量SL作為參考，可以相應設定不同的臨界電量值。如針對BESS放電運行設定一次臨界電量值Se1，二次臨界電量值Se2。當9P'落在區間（0.1C，0.2C）時，若SL＞Se1，則放電功率向上取值，PBESS=0.2C；若Se2＜SL＜Se1，則放電功率向下取值PBESS=0.1C；若SL＜Se2，則說明BESS系統剩余電量較少，放電功率需要進一步減小，取PBESS=0。

在負荷低谷時，同樣可以對BESS充電功率進行分檔匹配，同時設定臨界電量值Sf1。當SL＞Sf1時，充電功率向下取值，反之向上取值。

除以上設定之外，也可以結合區域負荷特點和BESS容量等因素，進行其他類型的詳細設置。以上分時分檔匹配流程如圖5所示。

通過以上每個時段對BESS充放電功率的具體分檔匹配，以及結合BESS剩余電量進行的功率具體選擇，即可以確定BESS全天的運行狀態。

2 區間控制方案算例

為了對以上控制方案進行驗證，可以搭建如下模型：采用圖1所示配電網，系統等效電源S基準電壓為10.5kV，容量為200MV·A。BESS從母線D接入，容量為S=30MW·h，最大充放電功率為6MW，BESS初始電量為Srem=3.5MW·h。Δt=6min，全天分為N=240個時段，能量均衡系數K=1.1。

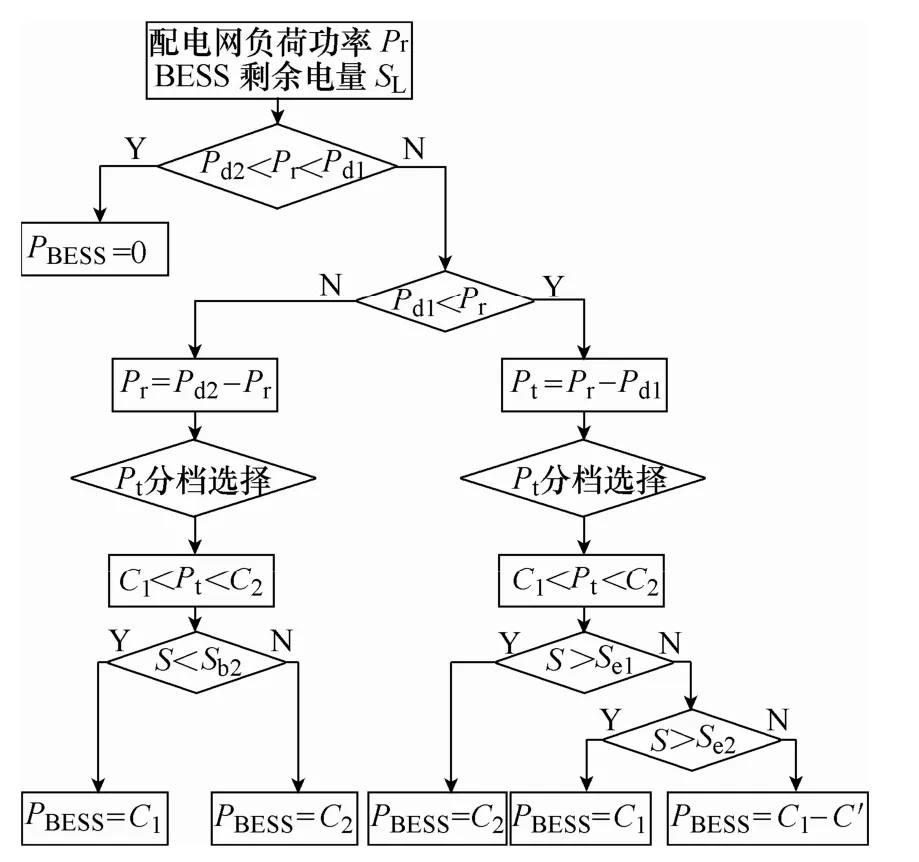
圖5 BESS具體充放電功率計算流程圖Fig.5 Calculation of the real-time exchange power of BESS

2.1 區間控制方案仿真

圖6所示為配電網日負荷曲線。假設預測負荷與實時負荷相同。負荷曲線在上午、下午各有一次負荷高峰，構成波峰段。凌晨為負荷低谷，構成波谷段。

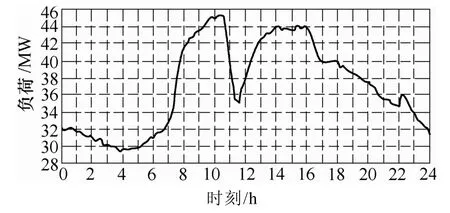
圖6 負荷曲線實例Fig.6 Example of load curve

2.1.1負荷控制區間確定

在負荷預測的基礎上，可求得日平均負荷P1=37MW。取迭代變量值ΔP=0.1MW，得邊際負荷值Pd=37.1MW。在此基礎上，求取負荷區間值Pd1和Pd2。

第一輪迭代計算保證BESS充放電量均滿足電池容量約束，取ΔP=0.1MW，通過迭代校驗，Pd1=39.7MW，Pd2=33.9MW。第二輪迭代保證電池充放電量的均衡，取ΔP'=0.05MW，通過迭代校驗，最終邊際負荷值為Pd1=40MW，Pd2=33.9MW。

2.1.2具體功率匹配

在確定了 BESS運行控制的區間之后，可以確定 BESS具體運行功率，即進行功率的分時分檔匹配。每Δt=6min進行一次功率匹配。

在BESS側，將充電運行和放電運行分別分檔，具體分檔及相應功率如下表所示。

表 BESS充放電分檔及對應功率Tab.Segments and corresponding power of BESS

對放電運行，設定一次臨界電量值Se1=0.5S=15MW·h，二次臨界電量值Se2=0.3S=9MW·h。對充電運行，設定臨界電量值Sf1=0.5S=15MW·h。

2.1.3仿真結果

通過仿真計算，可以安排BESS全天運行狀態及交換功率。圖7所示為仿真結果，上圖中虛線為原始負荷曲線，實線為經BESS削峰填谷后負荷曲線，兩條點畫線為負荷控制區間邊界；下圖為BESS剩余容量曲線，經過一天運行，BESS剩余電量S24=2.6MW·h。

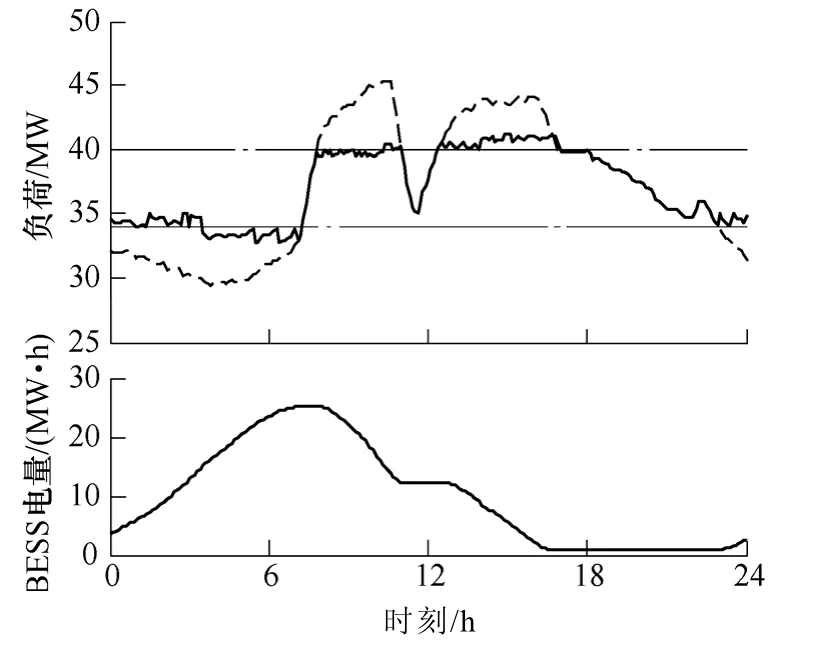
圖7 BESS區間控制優化效果圖Fig.7 Results of load interval controlling

從圖中可以看出，通過合理安排 BESS運行，可以很好地對日負荷進行削峰填谷，使負荷曲線維持在設定區間之內，不出現大的高峰和低谷。

2.2 連續周期運行效果驗證

由于 BESS用于削峰填谷是一個長期、連續的過程，因此有必要考慮接下來一天的控制結果，對連續周期運行效果進行驗證。

圖8所示為接下來一天BESS削峰填谷的運行效果。其中，Srem=2.6MW·h，Pd1=37.65MW，Pd2=31.4MW。圖中曲線定義與圖7相同，S24=3.686MW·h。

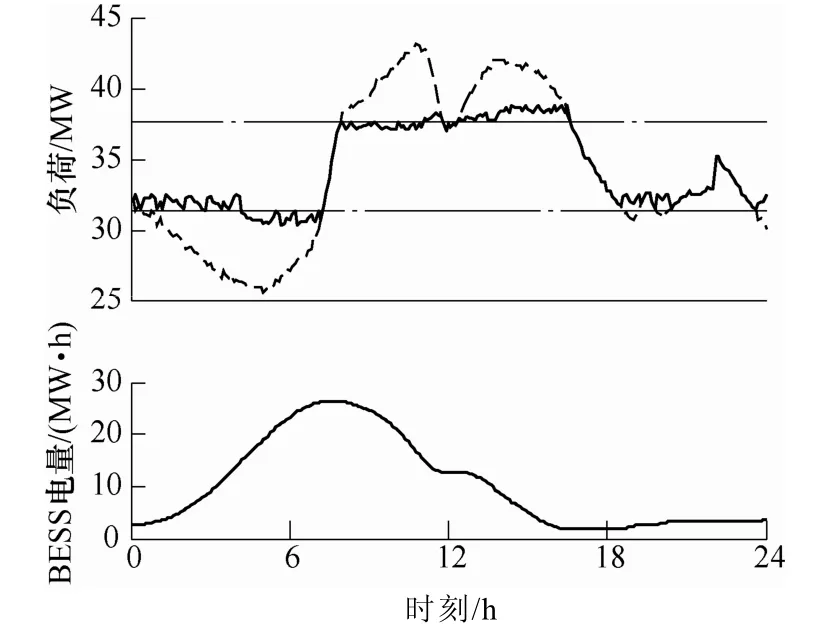
圖8 連續運行優化效果Fig.8 Result of continuous running

從圖中可以看出，該控制方案能夠很好地滿足連續運行的削峰填谷效果。由于控制方案考慮了BESS自身充放電量的均衡，因此對電池初始狀態的依賴很小。而靈活的區間設定也保證了該方案對不同的負荷曲線具有很好的適應性。

2.3 周期對控制效果的影響

上述分析中，對BESS的運行安排以24h為周期，每次安排未來一天的運行計劃。為了分析控制周期對BESS削峰填谷效果的影響，可以選擇新的周期進行仿真對比。將一天劃分為兩個時段，以 12h為一個周期，對BESS削峰填谷效果進行仿真。

2.3.1不同控制周期仿真

新的運行控制以12h為一個周期。仿真結果如圖9所示，圖中虛線為原始負荷曲線，實線為經過BESS削峰填谷后負荷曲線，兩組點畫線分別為T1和T2段負荷控制區間邊界；下圖為BESS剩余容量曲線。

圖9 兩段分別控制優化效果Fig.9 Load interval controlling with different cycle

從圖中可以看出，將控制周期設定為12h后，每個周期的期望負荷區間變窄。實際運行控制中，T1段的優化效果較好。與T1段相反，T2段的優化效果較差。在 15:00～17:00，負荷高峰仍然存在，而BESS剩余電量趨近于0，不能實現負荷削峰，導致第二個運行周期內削峰填谷失敗。

2.3.2運行控制周期選擇

通過對以上不同周期仿真結果的對比分析可知，在利用BESS進行負荷削峰填谷時，需要選擇合適的運行控制周期。因為BESS的削峰填谷能力是通過系統自身的充放電來實現，如果在選擇控制周期時不考慮負荷波動的特點，將會嚴重影響 BESS削峰填谷的效果。如對圖9中預測負荷曲線，若針對0:00～6:00和6:00～12:00時段分別進行BESS削峰填谷運行控制，則意義不夠明顯。因為這兩個時段分別為負荷低谷和負荷高峰，0:00～6:00只考慮充電運行，沒有考慮充電電量的釋放；反之，6:00～12:00只考慮放電運行，沒有考慮消耗電量的補充。分別考慮也對每時段 BESS初始電量提出較高的要求。

同時，由于對BESS系統的運行控制是連續的，因此，連續周期的波峰波谷應該交叉出現。若起始控制周期中負荷曲線是“谷?峰”出現，則下一周期也應該是“谷?峰”出現，同時配合BESS初始容量趨近于 0。反之，若起始控制周期中負荷曲線是“峰?谷”出現，則下一周期也應該是“峰?谷”出現，同時配合BESS初始容量趨近于滿容量。

在將一天分為兩個時段的控制方案中，雖然T1、T2段都有波峰波谷存在，可以滿足控制周期內BESS電量的自平衡，但是由于第一個時段負荷曲線“谷?峰”出現，第二個時段卻為“峰?谷”，才會出現在15:00～17:00時段 BESS初始容量不足導致削峰失敗的情況。長期來看，只有滿足波峰波谷交叉出現的連續周期，才能保證連續的削峰填谷效果。

由于常規電力負荷在一天內存在固有的波峰波谷，而且峰谷的出現有一定的規律性，因此以一天作為控制周期，可以在這個周期內實現BESS電量的自平衡，且能夠保證波峰波谷交叉出現的特點。

對于其他有長期削峰填谷需求的負荷，在選擇控制周期時，也應盡量滿足以上要求，以保證連續運行的效果。

3 BESS實時運行調整

以上分析及仿真均假設實時負荷與負荷預測相同。而在實際運行中，實時負荷與預測負荷之間會存在一定偏差，這會給BESS削峰填谷效果帶來很大影響。對基于負荷預測所制定的控制方案，需要根據實際運行中的實時負荷情況做出調整，以保證實際運行的削峰填谷效果。

3.1 實時調整策略

3.1.1實時調整前削峰填谷效果

圖10所示為配電網負荷曲線，其中虛線為預測負荷曲線，實線為實際負荷曲線。

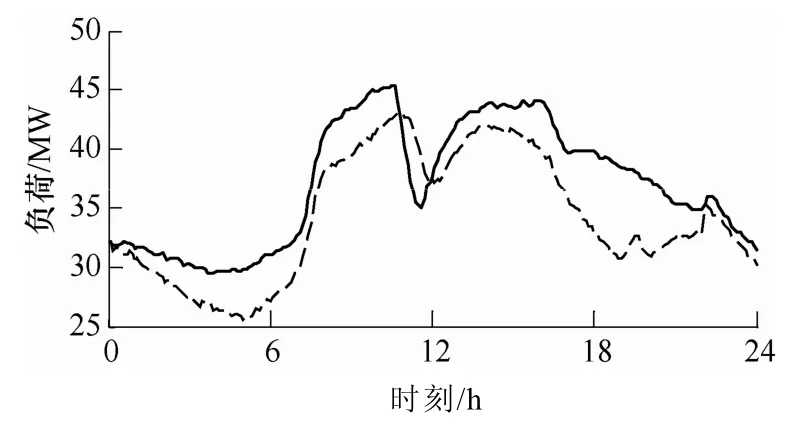
圖10 實時運行負荷曲線示意圖Fig.10 Diagram of real-time load curve

按照根據負荷預測設定的控制策略來安排BESS運行的效果，如圖11所示。從圖中可以看出，由于實際負荷的波谷、波峰均比預測值高，因此按照既定的控制方案來安排BESS運行，會導致在波谷時BESS充電不足，在波峰時沒有足夠的電量削峰。這一點可從圖11下部分圖中BESS電量曲線明顯看出，在早上7:00，由于BESS充電不足，電量只有 10MW·h；在中午 10:00左右，第一次負荷高峰結束之前，電量已基本放完，導致削峰失敗。

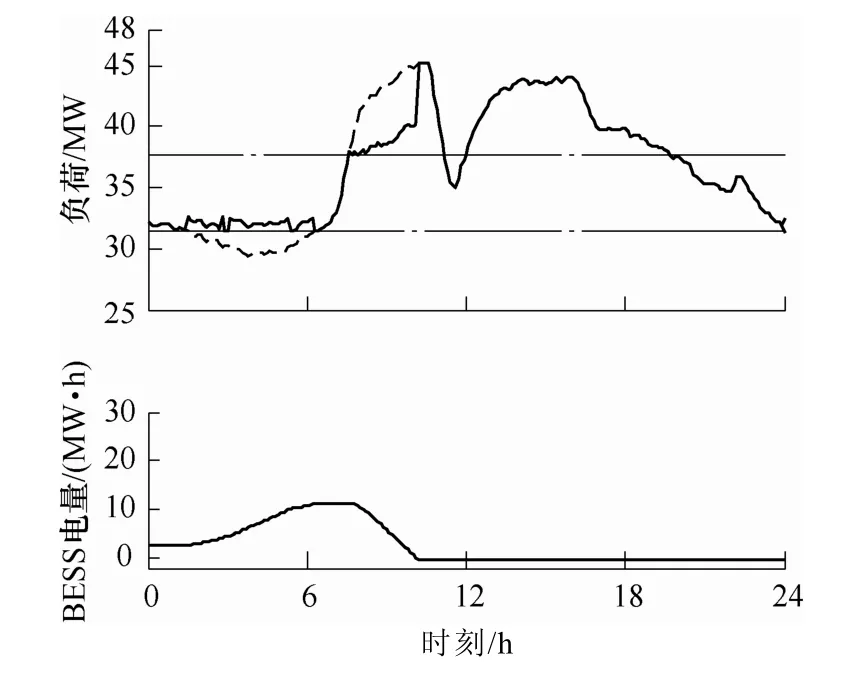
圖11 調整前效果Fig.11 Result of off-line controlling

3.1.2調整策略

為了保證BESS的削峰填谷效果，必須對BESS運行控制進行在線實時調整。在線實時調整以BESS電量預測值為基礎。在此基礎上，將全天分為三個階段分別進行BESS運行調整。

（1）0:00～7:00為第一階段，這一階段基本為全天的負荷低谷，BESS處于充電填谷狀態。實時調整以使BESS實時電量跟隨預測電量值，并盡量以充電為目標。具體實施時，每隔一段時間將 BESS實時電量與預測電量值進行對比，如果實時值偏低，則相應增大Pd2的值，反之減小Pd2的值。在負荷處于區間（Pd1,Pd2）之內時，若BESS沒有滿充，則以一定功率進行充電，以應對接下來的負荷高峰。

（2）7:00～17:00為第二階段，這一階段為全天負荷的高峰期，BESS需要有充足的電量進行負荷削峰。實時調整以使BESS實時電量不低于預測值，且在負荷較低時盡量充電為目標。具體實施時，同樣每隔一段時間將BESS實時電量值與預測電量值進行對比，如果實時值偏低，則相應增大Pd1的值，反之，保持Pd1不變，以保證最高負荷削峰優先。

（3）17:00～24:00為第三階段，這一階段負荷大多處于區間（Pd1,Pd2）之內。實時調整以使BESS實時電量小于設定值為目標，以保證BESS在第二天凌晨有足夠的負荷填谷能力。具體實施時，每隔一段時間調整BESS放電功率，以滿足設定目標。

BESS削峰填谷整體控制方案可以用圖12所示框圖表示。

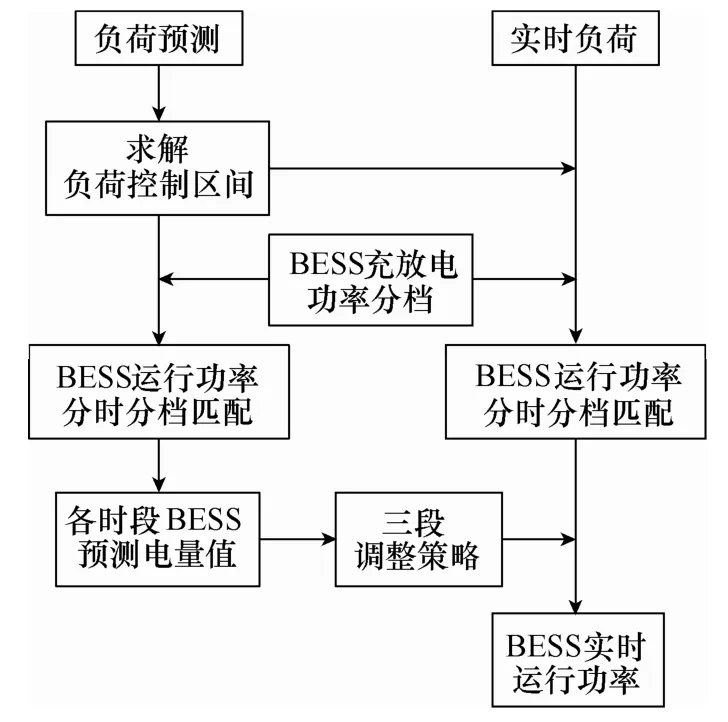
圖12 BESS削峰填谷整體方案Fig.12 Whole scheme of load shifting

其中，負荷預測支線為BESS實時運行控制打下基礎。在計劃方案中，可以根據預測負荷曲線求解出負荷控制區間，并預先求出全天BESS實時電量參考值。在實際運行中，將以求出的負荷控制區間為標準，對BESS充放電功率進行控制，并結合BESS電量預測值，根據調整控制策略，對 BESS實時充放電功率進行修正，以保證實時負荷與負荷預測存在偏差時，仍有較好的削峰填谷效果，盡量保證最高負荷的削峰。

3.2 實時調整效果

以Δt=6min為周期，對 BESS運行控制方案進行調整。Pd1和Pd2調整步長均為0.1。

圖13所示為最終效果，上圖曲線定義與圖 7相同，下圖中虛線為BESS電量參考值，實線為BESS實時電量值。

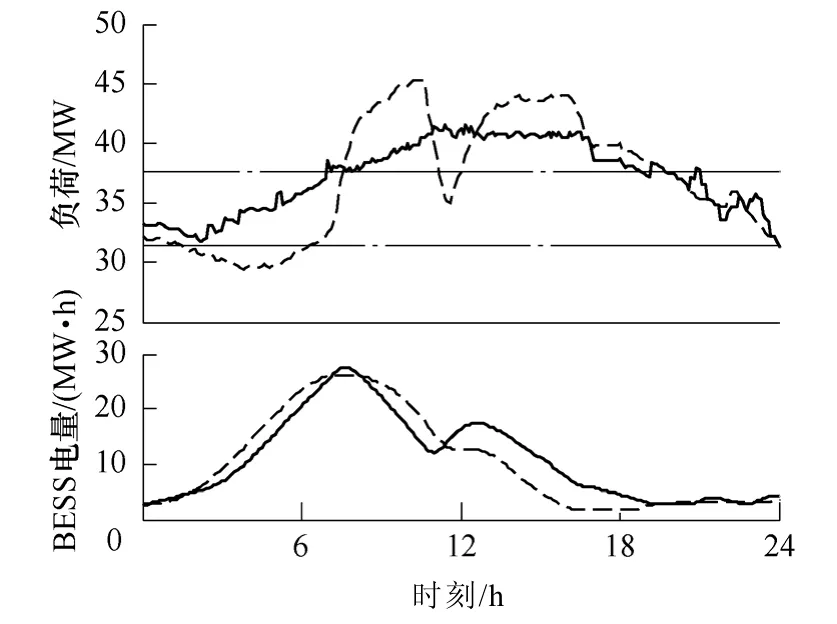
圖13 實時調整效果Fig.13 Result of real-time adjustment

從上圖可以看出，對BESS運行控制進行調整后，在實時負荷與預測負荷存在偏差的情況下，控制方案仍然能夠很好地實現負荷的削峰填谷，負荷曲線相對更平穩，高峰負荷時發揮了很好的削峰作用，BESS實時電量與預測電量的偏差不大。

從BESS運行控制的角度來看，調整前，BESS每Δt=6min進行一次功率匹配。而在線調整方案每次調整僅需引入 BESS現有容量與預測容量的值進行比較，再對邊際負荷值進行調整，BESS本身的充放電功率計算方法基本保持不變，所以，調整算法的計算量很小，簡單易行。

在進行實時調整時，選擇與BESS功率匹配周期相同的實時調整周期相對是最優的，這不僅保證了調整方案的高準確度和良好的優化效果，也不需要增加太多計算量。

4 結論

針對儲能系統對配電網負荷削峰填谷的運行控制問題，本文首先從負荷預測的角度，提出了基于負荷區間的削峰填谷控制策略。以BESS容量以及充放電量均衡為約束，通過迭代計算得出削峰填谷的負荷控制區間，并將負荷曲線與預測值的差值和離散化的BESS運行狀態進行分時分檔匹配，最終確定BESS的具體運行，使負荷穩定在期望區間內。仿真結果驗證了該控制策略的有效性。

在此基礎上，本文還對BESS削峰填谷控制周期的選擇進行了一定研究。對固定特點的負荷，應保證控制周期內同時存在波峰和波谷。同時，為了保證控制的連續性，連續周期的波峰、波谷應該交叉出現。最后，針對實時負荷與預測負荷存在偏差的問題，本文提出了基于BESS電量預測值的調整運行方案。通過仿真驗證了調整方案的有效性。

BESS最大儲能量也會直接影響其削峰填谷的效果，根據本文所提出的控制策略，BESS容量越大，削峰填谷的負荷控制區間越窄，負荷越平穩。然而，增大BESS容量會大大增加建設成本。負荷區間越窄，波谷和波峰時對 BESS充放電功率的要求越高，技術要求也相應提高。因此，針對某一特定區域的負荷，為達到預定的削峰填谷控制目標，存在BESS容量的最優值，可以結合區域歷史負荷以及未來負荷變化趨勢，綜合考慮技術和經濟因素，尋求最優BESS容量值。

[1] 周林,黃勇,郭珂,等.微電網儲能技術研究綜述[J].電力系統保護與控制,2011,39(7):147-152.

Zhou Lin,Huang Yong,Guo Ke,et al.A survey of energy storage technology for microgrid[J].Power System Protection and Control,2011,39(7):147-152.

[2] 廖勝利,程春田,蔡華祥,等.改進的火電調峰方式[J].電力系統自動化,2006,30(1):89-93.

Liao Shengli,Cheng Chuntian,Cai Huaxiang,et al.Improved algorithm of adjusting discharge peak by thermal power plants[J].Automation of Electric Power System,2006,30(1):89-93.

[3] 王鵬,張靈凌,梁琳,等.火電機組有償調峰與無償調峰劃分方法探討[J].電力系統自動化,2010,34(9):87-91.

Wang Peng,Zhang Lingling,Liang Lin,et al.A method for division of paid peak-regulation and free peakregulation for thermal power units[J].Automation of Electric Power System,2010,34(9):87-91.

[4] 張少華,言茂松.上海電網發展燃氣輪機調峰的系統規劃與優化[J].電網技術,1996,20(4):27-32.

Zhang Shanghua,Yan Maosong.Systematic planning and optimization for GAS turbine plants in Shanghai power system[J].Power System Technology,1996,20(4):27-32.

[5] 王若谷,王建學,張恒,等.水電機組調峰服務的成本分析及實用補償方法[J].電力系統自動化,2011,35(23):41-47.

Wang Ruogu,Wang Jianxue,Zhang Heng,et al.A cost analysis and practical compensation method for hydropower units peaking service[J].Automation of Electric Power System,2011,35(23):41-47.

[6] 王金文,范習輝,張勇傳,等.大規模水電系統短期調峰電量最大模型及其求解[J] 電力系統自動化,2003,27(15):29-34.

Wang Jinwen,Fan Xihui,Zhang Yongchuan,et al.Short-term generation schedule for the peak-energy maximization of large-scale hydropower systems[J].Automation of Electric Power System,2003,27(15):29-34.

[7] Ali Nourai,Kogan V I,Chris M Schafer.Load leveling reduces T&D line losses[J].IEEE Transactions on Power Delivery,2008,23(4):2168-2173.

[8] Sutanto D.Power management solutions for energy management,power quality and environment using battery energy storage systems[C].IEEE 1999 International Conference on Power Electronics and Drive Systems,Hong Kong,1999,1.

[9] Zhou Haihua,Tanmoy Bhattacharya.Composite energy storage system involving battery and ultracapacitor with dynamic energy management in microgrid applications[J].IEEE Transactions on Power Electronics,2011,26(3):923-930.

[10] 丁明,徐寧舟,畢銳.用于平抑可再生能源功率波動的儲能電站建模及評價[J].電力系統自動化,2011,35(2):66-72.

Ding Ming,Xu Ningzhou,Bi Rui.Modeling of BESS for smoothing renewable energy output fluctuations[J].Automation of Electric Power System,2011,35(2):66-72.

[11] Jeroen Tant,Frederik Geth,Daan Six.Multiobjective battery storage to improve PV integration in residential distribution grids[J].IEEE Transactions on Sustainable Energy,2013,4(1):182-192.

[12] 嚴干貴,馮曉東.用于松弛調峰瓶頸的儲能系統容量配置方法[J].中國電機工程學報,2012,32(28):27-36.

Yan Gangui,Feng Xiaodong.Optimization of energy storage system capacity for relaxing peak load regulation bottlenecks[J].Proceedings of the CSEE,2012,32(28):27-36.

[13] Igor Papic,Member.IEEE simulation model for discharging a lead-acid battery energy storage system for load leveling[J].IEEE Transactions on Energy Conversion,2006,21(2):608-616.

[14] Ali Nourai,Kogan V I,Chris M Schafer.Load leveling reduces T&D line losses[J].IEEE Transactions on Power Delivery,2008,23(4):2168-2173.

[15] Oudalov A Cher kaoui R,Beguin A.Sizing and optimal operation of battery energy storage system for peak shaving application[C].2007 IEEE Lausanne,Power Tech.,2007:621-625.

[16] Palomino E,Stevens J,Wiles J.A control system for improved battery utilization in a PV-powered peakshaving system[C].IEEE Conference Photovoltaic Specialists Conference,Washington DC,1996:1525-1528.

[17] Jeroen Tant,Frederik Geth,Daah Six.Multiobjective battery storage to improve PV integration in residential distribution grids[J].IEEE Transactions on Sustainable Energy,2013,4(1):182-192.