中國國債期貨定價研究
——基于交割期權修正方法

曾耿明

(中國中投證券博士后工作站，廣東 深圳 518000)

引言

傳統期貨定價理論認為期貨的價格為現貨價格加上持有現貨的成本。例如，股指期貨的價格等于股指的現貨價格加上持有現貨的資金利息成本，如果該關系不成立，則市場就可以通過做多現貨做空期貨或做空現貨做多期貨方式進行無風險套利。然而，國債期貨的合約設計和傳統的期貨合約存在諸多顯著差異，導致國債期貨的定價如果簡單地運用該理論模型就會產生一定的偏差。首先，國債期貨的合約標的是虛擬的國債現貨，如中金所的國債期貨合約規定其標的合約為5年期的到期收益率為3%的國債現貨，然而滿足該合約條件的國債現貨在市場中并不一定存在，代替其交割的標的國債是期限為4～7年期的國債現貨，簡稱為可交割券。其次，持有國債期貨的空頭在到期交割時可以選擇對自己最有利的可交割券進行交割，相當于期貨合約內嵌了一個有利于空頭的隱含期權合約。

因此，本文根據中金所國債合約的設計條款研究建立以交換期權模型為基礎的國債期貨轉換期權價值模型，試圖得到一個更加適合我國國債期貨合約設計狀況且更加精確的定價方程。

在學術文獻上，Margradbe(1978)[7]闡述了對資產交換期權進行定價的方法。Gay等(1984)[3]利用William交換期權的定價方法為商品期貨合約中的質量期權進行定價建模。Hemler(1990)[6]提出使用交換期權的定價方法來實現為國債期貨的隱含期權進行定價，但是由于我國國債期貨合約條款和美國存在諸多差異，該模型并不完全適合我國國債期貨市場。Grieves and Marcus(2005)[4]利用交換期權的定價方法為只含有兩個可交割券的交割期權定價，并研究了這種期權的存在對套期保值效果的影響。Richard and Rendleman(2004)[8]采用BDT模型為即期無風險利率建模，從而得到了包含擇券交割期權的國債期貨價格，相應得到擇券交割期權的價值。Abdallah等(2012)[1]同時考慮了擇時交割期權和擇券交割期權來為國債期貨合約定價。Balbas and Reichardt(2010)[2]采用了無套利的方法從市場價格中提取擇券交割期權的價格。Grieves等(2010)[5]對兩個可交割券的交割期權進行實證檢驗，發現只包含兩個可交割券的交割期權定價方法能夠吻合國債期貨的市場價格特征。

國內對國債期貨的研究較多集中在制度與市場建設上，如張慶修和趙文杰(1994)[13]、蔣錦志(1995)[10]對我國90年代早期的國債期貨市場進行了概述，鄭權(1995)[14]對美國國債期貨市場的發展經驗進行了研究，王敬(2013)[12]等對中金所國債期貨的合約設計進行了研究。關于我國國債期貨隱含交割期權建模研究的文獻較少，這是由于我國國債期貨是于2013年9月6日才重新上市的，歷史時間較短。康凱和潘進(2014)[11]利用線性回歸模型研究國債期貨定價與交割期權的實證關系，但并未對交割期權提出定價模型。陳穎(2012)[9]探討了國債期貨的轉換期權，但只是定性的研究，并沒有做定量和模型分析。周子康等(2008)[15]等對國債期貨的最便宜交割債券進行分析，但并未對國債期貨的隱含期權價值進行探討。

因此，本文首次提出了基于我國國債期貨隱含交割期權的模型分析和實證分析，并將其用于修正傳統國債期貨定價的偏差。通過對市場數據的實證檢驗，發現本文的修正方法在一定程度上減少了國債期權的定價偏差。

中國國債期貨合約特征

2013年8月30日中金所發布了5年期國債期貨的業務規則，并于2013年9月6日正式在中金所掛牌上市，標志著我國國債期貨自1995年“327”事件被停止后，重新返回歷史舞臺。與之前的國債期貨合約設計不同，此次合約為防范市場價格被人為操縱融入了更嚴格的限制條款。

5年期國債期貨的掛鉤標的是面值為100萬元人民幣、票面利率為3%的名義中期國債。由于國債期貨采用實物交割方式，在真實市場中未必能找到剛好滿足該條件的標準券進行交割，因此中金所采用合約到期月首日剩余期限為4～7年的記賬式附息國債作為可交割券來替代標準券。到交割日時，期貨的空頭可以在一籃子可交割券中選擇對自己最有利的一支可交割券進行實物交割。然而，不同可交割券的票面利率、剩余期限存在著差異，因此通過轉換因子系數將可交割券的到期收益率和標準券進行統一。在數學上，轉換因子定義為面值1元的可交割國債在假定到期收益率為標準券利率3%時其在期貨合約上市日的凈價。中金所會在每個國債期貨合約上市時公布轉換因子表。國債期貨交割方式為實物交割，交割方式分為滾動交割和集中交割。滾動交割指當季合約進入交割月份后至最后交易日之前申請的交割，集中交割是指合約最后交易日收市后的未平倉部分按照交易所的規定進入交割。具體合約條款、轉換因子系數和交割清算公式均可在中金所網站查閱得到。

國債期貨的交割期權

國債期貨合約的交割制度賦予期貨空頭一系列選擇權，具有期權的屬性，在對國債期貨進行定價時需充分考慮到該類期權的市場價值。如果忽略這些隱含期權的價值，可能導致交易策略失效。例如，在利用國債期貨對現貨套期保值時，如果忽略最便宜可交割券的變動，很可能導致計算的對沖比例和現貨的風險暴露頭寸不匹配，使得套期保值失效。下文根據中金所國債期貨合約的條款，對該類隱含的交割期權進行分析。

一、隱含交割期權種類

國債期貨空頭的隱含交割期權主要包括轉換期權、時機期權和月末期權。

轉換期權是指在合約的交割月份中，期貨的空頭可以選擇一支最便宜的交割券(簡稱CTD券)用于最終交割，實現交割成本的最小化。CTD券并不是一成不變的，而是隨著期貨價格、現貨價格、到期期限的變化可能發生變化。期貨空頭方可以購入更低價格的交割券替代原先的CTD券完成交割，并從中賺取差價獲利。正是該或有收益構成了轉換期權的到期收益。該轉換期權主要與可交割債券的利率波動、到期期限等因素相關，是國債期貨空頭隱含交割期權最重要的構成部分。

時機期權來自投資者有權在第一個可交割通知日到最后交割日之間的任意一天提出交割申請，空頭方可以選擇一個現貨價格較低的時點提出交割申請，以獲取更低的交割成本。

月末期權來自期貨交割價格和最終交割日之間的時滯。在合約月份中，最后交易日到最終實物交割日之間，仍有若干個交易日。在逐日盯市制度下，期貨價格被鎖定在最后交易日，因此空頭方可以在最終交割日之前選擇一個有利時點來買入最便宜的債券。

圖1總結了三個期權的主要特征，轉換期權是從期貨合約上市日到最后交易日空頭方有權選擇CTD券的權力，時機期權是從期貨交割月首日到最后交易日空頭方有權選擇CTD券的權力，而月末期權則是從期貨最后交易日到最終交割日空頭方有權選擇CTD券的權力。

二、隱含交割期權估值

盡管目前中金所的國債期貨存在著諸多嵌入期權價值，但合約交割制度同樣限制了時機期權和月末期權的價值。首先，對于時機期權，在滾動交割階段，空頭和多頭都可以提出提前交割的申請，但只有在配對成功后才能進入交割，如果提前交割只對交易的一方有利時，交易的另一方則可以選擇推遲交割，使得提前交割配對無法實現，因此，時機期權對于我國國債期貨價值可以近似忽略。其次，對于月末期權，由于我國國債交易集中于銀行間市場，交易所市場交易比較清淡，銀行間市場買賣的國債在交割時需由中債登劃轉到中證登，至少需要3個交易日，所以國債期貨中月末期權的時滯性相對于銀行間市場國債轉托管的時間變得無意義。即便是交易所市場的債券，期貨交易結束后也只有半個交易日可以用于購買交割券，對空頭獲利的空間也非常有限，因此月末期權的價值也可以近似忽略。

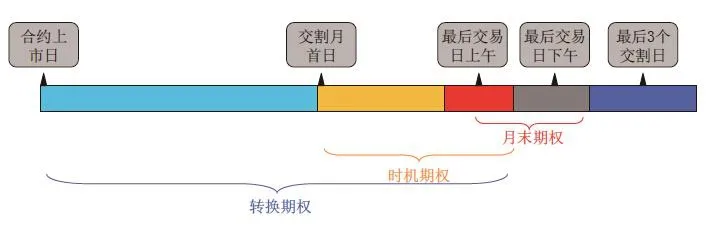
圖1 交割期權比較

綜上分析，目前對我國國債期貨價值影響最大的隱含期權是轉換期權。轉換期權的價值來源于當前CTD券是否會在最后交割日發生變動，如果發生變動則意味著期貨空頭可以用更加便宜的CTD券來進行交割，從而獲利。

三、轉換期權的定價模型

目前，市場中確定CTD券的最常用方法是隱含回購利率最大化。隱含回購利率是指通過計算當前買入可交割券，同時按當前期貨價格賣空國債期貨，持有到交割日并用于最后交割，所能夠獲得的實際收益率。該實際收益率越高，表明該可交割券的交割成本越低。隱含回購利率的計算公式如下：

其中Ft為t時點國債期貨價格，CF為轉換因子AIT為上一付息日到交割日可交割券的應計利息，Bt為t時點的可交割券凈價，AIt為上一付息日到t時點的可交割券應計利息，n為時點t到交割日的天數。表1顯示了TF1503在銀行間市場的可交割券在2014年12月9日時點的隱含回購利率列表，表中顯示‘13付息國債15’為該時刻的最便宜可交割券。

隱含回購利率的公式(1)顯示，隨著債券價格Bt或期貨價格Ft的變化，IRR也是在不斷變化，因此，CTD券隨著市場的變化可能會發生變化。但是由于可交割券的期限、到期收益率和風險因子相近，不同可交割券的價格Bt波動相關性較強，而期貨價格Ft對不同可交割券均一致，因此不同可交割券的IRR波動也具有較強相關性。正是這樣，不同可交割券的IRR排序變化并不平凡，在交割時次便宜交割券最有可能替代當前的CTD券，可以解釋總體轉換期權價值的絕大部分。因此，本文建模時將基于一籃子交割券的轉換期權簡化為基于兩個次便宜交割券的最小值看跌交換期權。

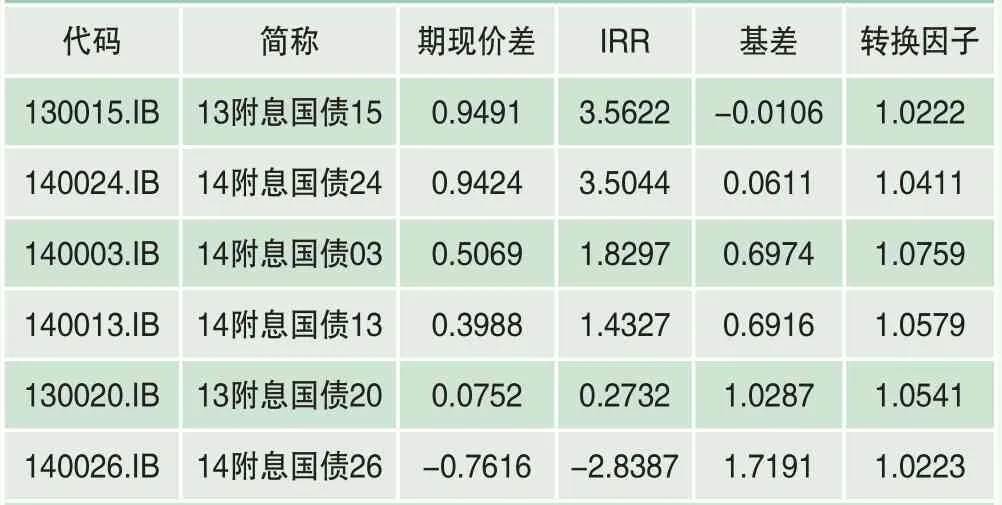
表1 TF1503可交割券的隱含回購利率(2014-12-9，銀行間市場)

在設立模型時，假設只有兩個交割券能夠成為交割時的最便宜交割券，其中交割券1是當前的CTD券，交割券2為次便宜交割券。例如，在表1的交割券1為‘13附息國債15’，而交割券2為‘14附息國債24’。當國債期貨進入交割時，交割券2可能替代交割券1成為新的CTD券。

其中Ft為期貨價格，CF1為交割券1的轉換因子，B1,t為交割券1在t時刻的凈價，AIt～T為t到T期間的債券利息收入。如果發生CTD券轉移，交割券2成為新的CTD券，則空頭將買入份新的CTD券(交割券2)代替原來的CTD券(交割券1)進行交割，并在二級市場上賣出原CTD券，空頭總獲利為：

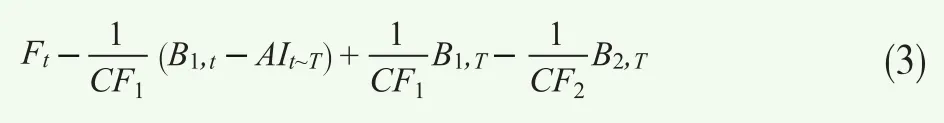
其中CF2為交割券2的轉換因子，B2,T為交割券2在交割時的凈價。對(3)和(2)式做差就是期貨空頭因持有隱含轉換期權到期時的獲利，即

另外，假設模型中兩支可交割券的凈價服從幾何布朗運動，即

其中dW1,t和dW2,t是相關系數為σ的維納過程。在這些模型假設下，本文參考William(1978)對股票資產交換期權的基本模型，求解得到國債期貨轉換期權價格的封閉解析解為：

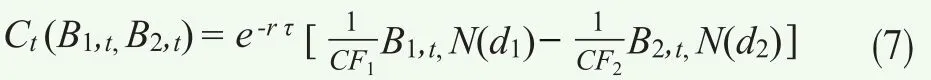
其中

基于轉換期權修正的國債期貨定價方程

假設國債期貨不存在著交割期權，則國債期貨的理論價格滿足一般的期貨定價方程，即CTD券的凈價加上其持有成本并除以轉換因子，其數學表達式為如下公式：

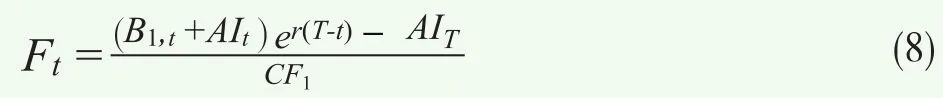
其中B1,t+AIt為t時刻購買CTD券的全價，AIT為上一付息日到交割日CTD券的應計利息。

由上文分析知，我國國債期貨的空頭擁有隱含的轉換期權價值，因此我們對我國國債期貨定價時，需要對傳統的定價方程(8)的現券購買成本進行修正，即在原先的理論價格減去隱含期權價值，具體方程表達式如下所示：

對我國國債期貨市場的實證分析

本文通過建立的模型對我國國債期貨的價格形成機制進行實證分析。選取的國債期貨合約樣本為TF1503，樣本區間為該合約的交易初始日2014年7月3日～2014年12月23日，總共120個樣本數據。Wind數據庫給出了對TF1503期貨CTD券的統計數據，在樣本期內，成為該合約CTD券次數最多的是‘11付息國債15’，其轉換因子為1.056；其次是‘14付息國債13’，其轉換因子為1.0579，因此，這里我們可以近似將這兩支交割券作為本文轉換期權模型的兩支可交割券。

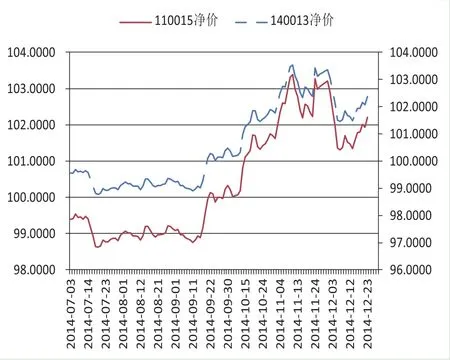
圖2 CTD券和次CTD的凈價走勢(數據來源Wind)

圖2顯示了‘11付息國債15’和‘14付息國債13’在我國銀行間交易市場的凈價走勢，顯然兩支交割券的走勢高度相關，這是由于國債期貨的可交割券具有相似的產品結構屬性，如國債的到期期限、到期收益率等。通過該樣本數據對方程(5)和(6)進行參數估計，選取的估計方法為：

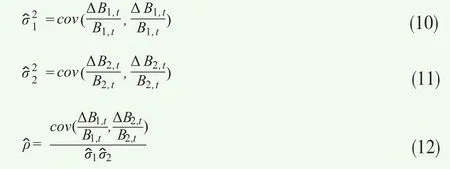
表2顯示了模型參數的估計結果，兩支可交割券的波動率參數非常接近且相關系數為0.99，說明兩支可交割券的波動高度相關。本文在樣本期間內市場的無風險利率選取為1年期定期儲蓄存款基準利率3%，則通過國債期貨可轉換期權的定價模型(7)以及參數估計值可以計算出TF1503隱含的可轉換期權的價值。

表2 模型參數估計結果

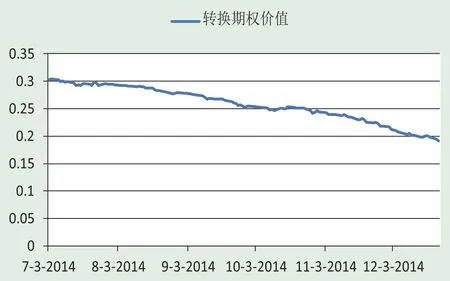
圖3 TF1503轉換期權價值

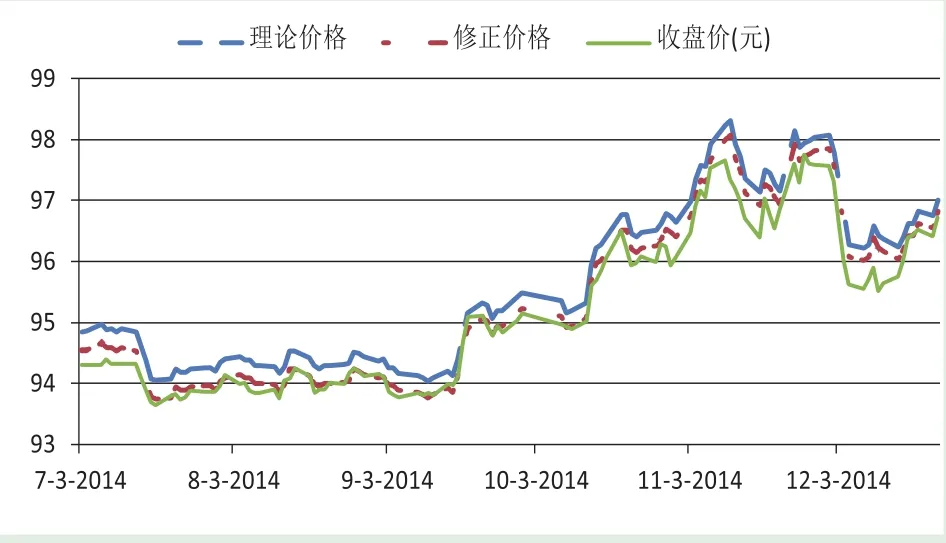
圖4 TF1503理論價格、修正價格和當日國債期貨收盤價比較

圖3顯示了根據模型(8)計算的國債期貨TF1503隱含的轉換期權價值。在樣本期內，該期權的價值平均值為0.257，日波動率為0.031。圖3還顯示該轉換期權的價值隨著到期日的不斷臨近而不斷減少，這是由于期權的時間價值隨著到期日的不斷臨近在不斷流逝。

完成對轉換期權價值的估算，我們可以通過本文修正的國債期貨定價方程(9)來估計國債期貨的理論價格。圖4顯示了通過傳統期貨定價方程(9)計算的國債期貨理論價格(圖中的標示為“理論價格”)、本文轉換期權價值修正的國債期貨修正價格(圖中的標示為“修正價格”)以及TF1503期貨市場收盤價。圖中顯示國債期貨的理論價格和修正的理論價格均與國債期貨的收盤價吻合得較好，說明期貨市場和現貨市場保持較高相關性的價格趨勢。圖中還顯示轉換期權價值的修正能減小一部分基差，通過轉換期權修正的國債期貨理論價格曲線和比傳統的理論價格曲線更加吻合TF1503期貨的市場價格曲線。這里我們用均值誤差平方根(RMSE)1指標來度量兩者之間的定價誤差。傳統期貨定價方程的理論價格與市場價格的平均定價誤差RMSE為0.2112，而本文修正的期貨理論價格與市場價格的RMSE為0.0596。因此，RMSE的大小比較分析表明修正的理論價格定價誤差顯著小于傳統的期貨定價模型。

總結

為了規避國債期貨交割時的逼倉風險，中金所在對國債期貨合約的設計時采用了一籃子可交割券交割、滾動交割等一系列交割制度，使得傳統的期貨定價方程會對國債期貨實際價值的估計產生偏差，這是由于其忽略了國債期貨合約自身隱含的各類期權價值。本文通過對國債期貨隱含的各類期權價值進行分析，發現國債期貨空頭在交割時會在一籃子可交割券中選擇最廉價的現券進行交割，其等價于期貨空頭方持有一個以可交割券為一籃子資產的交換期權，基于此，本文首次建立了我國國債期貨的轉換期權估值模型，并將該模型融入到國債期貨傳統的定價方程。對樣本的實證研究表明，該修正模型計算的理論價格不僅與國債期貨的市場價格高度一致而且比傳統的定價模型減少了定價誤差。

注釋