高中數學解題中“巧”的魅力

陳金銘

【摘 要】高中數學是高中教育課程體系中的重要組成部分，它經常被視為難度系數最高的一門學科，在解題過程中，學生經常會出現無從下手的現象。在實際教學過程中，我們不難發現，對高中數學進行“巧”解，不僅能加快解題速度，而且能為解題提供一個全新的思路。本文從具體實例出發，詳細介紹高中數學解題中“巧”的魅力，從而達到提高整體高中數學教學質量的目的。

【關鍵詞】高中數學 ? ? ?解題 ? ? “巧”解

當今教育話題成為全民探討的熱門話題。無論是各大影視廣受關注，還是不同教育學校相繼建成，都表達了人們對教育事業的重視程度。隨著我國對素質教育的推行，對教育的改革力度也正在逐步加強。高中數學作為教育事業的重中之重，它的教學成果顯得尤為重要。它不僅直接關系著學生高考的成績，更與人們在日常生活中的實際應用密不可分。然而，高中數學并不等同于小學、初中數學，其題型往往更加復雜、解題過程更加煩瑣。要想實現解題中“巧”的效果，則應從數學概念、題目信息、解題思路三方面著手。

一、明確數學概念，尋找“巧”解方法

要想實現高效解題，則必須對數學知識做到全面掌握。高中數學概念同樣包含其中，不僅要做到全面理解，還要學會靈活運用。在很多高中數學解題中，從最基礎的數學概念入手，往往可以取得意想不到的突破，最大限度地提高解題效率。

實例一：已知tanα=，求（cosα+sinα）/（cosα-sinα）的值。該題屬于常見的三角函數題型，是有關正弦函數、余弦函數、正切函數之間的數學知識點。在常規解題過程中，學生經常會被外部形式給難倒，忽略了它們三者之間的內部關系，從而導致解答很久都無法算出正確結果。所以，我們要從概念著手，分析它們的內部聯系，對其概念進行很好的利用。在三角函數中，正切值等于正弦值與余弦值的商，即tanα=sinα/cosα，再聯系sin2α+cos2α=1，可以將（cosα+sinα）/（cosα-sinα）可以轉化成（1+sinα/cosα）/（1-sinα/cosα），即所求函數式可以表示為（cosα+sinα）/（cosα-sinα）=（1+sinα/cosα）/（1-sinα/cosα）=（1+tanα）/（1-tanα）=（1+）/（1-）=-3-2，最后得出結果。對數學概念的巧妙運用，使解題思路更加清晰化，推理過程準確無誤，運算量大大減少。

二、分析題設信息，獲取“巧”解途徑

在數學學習過程中，我們經常看到很多學生死記公式以便在加快解題效率，但是常常會出現亂用公式、錯用公式的現象。究其原因，就是忽略了對題目信息的審核，缺乏一定的嚴謹性，從而掉進了題設“陷阱”當中。所以，在解答數學題時，一定要避免機械化的學習，要做到對信息內容的分析，從而使題目迎刃而解。

三、“巧”用數形結合法，變換解題思路

在數學解題過程中，數形結合法是一種必不可少的解題策略，該思路能將看起來較為復雜的數學題目更加直觀形象地表達出來，一定程度上提高了解題時的理解能力，化繁為簡、化難為易，為“巧”解題目奠定了良好的基礎。關于這一新思想，早在很多年前，華羅庚也對其進行了肯定。這一方法的具體應用，可以通過實例二表示出來。

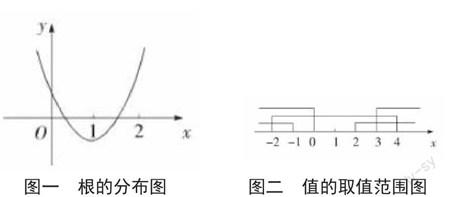
實例二：已知方程6x2-（m+11）x+m2-m=0的兩個實根x1、x2滿足00，f（1）<0，f（2）>0。用數據表達為m2-m>0，m2-2m-5<0，m2-3m+2>0，得出最后結果-2

圖一 ?根的分布圖 ? ? ? ? 圖二 ?值的取值范圍圖

通過圖象觀察，我們不僅可以在解題前對題目有更深層次的理解，還可以對其結果有更直觀地了解。數形之間達到巧妙的結合統一，可以讓學生在學習過程中更加輕松，有效提高了學生的創新思維，為學生的數學解題思路開拓了一個新的途徑，對他們的能力提高有促進作用。

四、結束語

總體來說，在高中數學解題時，“巧”的魅力體現在方方面面，有效應用“巧”解策略可以達到提高數學成績的良好效果。對于學生而言，在解題過程中，要積極努力尋找“巧”的魅力所在，敢于突破常規思維，從多重理解上進行解題。對于老師而言，在教學過程中，要注重培養學生“巧”解數學的能力，使其技能得到提高，并且要將“巧”解思想應用到具體實踐中去，加大對學生該能力的培訓力度，使學生運用自如。作為一種新型解題策略，“巧”解魅力發揮著持久不散的作用，它在整個教學領域中都應該得到推廣，而不僅僅只是對高中數學而言。只有將其應用到每一門課程的教學之中，才能使學生更加全面發展，提高學生的綜合能力，從而提高整體教學水平，為我國的教育事業發展起到推波助瀾的作用。

【參考文獻】

[1]楊子清，溫培珠.初中數學解題方法與技巧教學的研究[C].中華教育理論與實踐科研論文成果選編（第三卷），2012，32（11）：489-490.

[2]鄭亞軍，張雪萍，祁美萍.數學解題常見錯誤例析[C].萃英集——青海省教育委員會、青海省教育學會優秀教育論文集，2012，20（09）：667-668.

[3]蘇少卿，錢斌，馮紅果.中學生數學解題效率成因研究[C].全國高師會數學教育研究會2006年學術年會論文集，2012，30（03）：603-604.