層次分析法在評估三本院校教師綜合能力中的應用

易 強 呂希元

（重慶工商大學融智學院，重慶 400033）

層次分析法在評估三本院校教師綜合能力中的應用

易 強 呂希元

（重慶工商大學融智學院，重慶 400033）

本文利用層次分析法對三本獨立學院的教師進行年終考核，期望對所考察教師作優劣的排序，以便做到優勝劣汰，選拔能力強的骨干，剔除不稱職的教師。

層次分析法 績效考核 指標 判斷矩陣

績效考核就是對教師全面綜合評價，它能夠直接反映教師的綜合能力，是關系到教師的工資待遇、職稱評定和升職的一種手段。

年終考核是對教師進行多指標綜合分析的復雜體系。在綜合考核過程中需要解決三個方面問題：一是要求避免人的主觀因素的影響；二是確定各項指標在考核過程中的相對重要程度；三是對每項指標直接進行定量綜合分析。利用層次分析法可以較好地解決此類問題。

層次分析法是融合了定量與定性的系統分析法。它通過對人的思維進行層次化、數量化處理，再用數學方法為分析、決策、預報或控制提供定量的依據。這種數學方法在對解決多因素權重的確定或是多個決策方案的擇優排序上相當易于控制而又行之有效。

建立層次分析法，其基本步驟如下：

（1）建立層次分析法的結構模型；

（2）構造判斷矩陣；

（3）層次分析單排序和一致性檢驗；

（4）層次分析總排序和一致性檢驗。

1.建立層次結構模型

1.1 層次結構圖

為了評估三本院校專職教師的綜合表現，根據三本院校教師工作特點，我們首先確定績效考核優劣排序的層次結構如下：

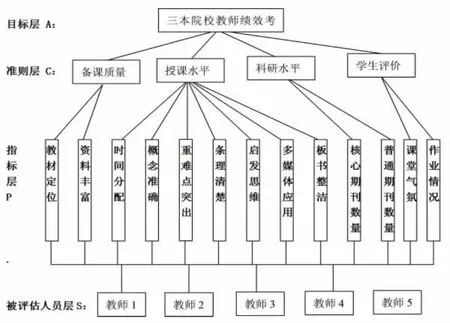
1.2 指標項的確定理由

根據影響三本院校教師績效考核的各因素，將層次結構圖分為三級指標。對三級指標層中13項指標的各項解釋如下。

P1教材定位：考察教師在課堂教學中對于教材的把握是否到位；

P2資料豐富：考察教師在備課時資料準備的是否豐富；

P3時間分配：根據三本院校學生的記憶曲線規律，教師應適當安排教學時間，使得學生吸收情況最優；

P4概念準確：考察教師在講課過程中，對概念的講解是否準確、清楚，對概念的把握是否恰當；

P5重難點突出：考察教師在授課過程中，對教學大綱中規定的重點、難點把握是否清楚，對重點、難點的講授安排是否恰當；

P6條理清楚：考察教師在授課過程中對教材內容的安排是否有條理；

P7啟發思維：考察教師在授課過程中所采用的教學方法能否有效啟發學生的思維，激發學生的想象力和創造力；

P8多媒體應用：考察多媒體教學設施的使用是否恰當，能否使課堂教學取得最大效益；

P9板書整潔：考察教師在授課中所板演的內容能否做到字跡清楚，圖形規則，板書工整、有條理；

P10核心期刊數量：考察教師的科研水平，是作為提拔教師的一個重要指標；

P11普通期刊數量：考察教師對于科研方面是否有所投入；

P12課堂氣氛：通過對學生的課堂反映、課堂回答等方面綜合考評，考察教師對于課堂的整體把握能力；

P13作業情況：通過對學生作業完成情況（包括質量、數量等）的考察，借以評估教師在講解知識時學生的吸收情況。

2.建立判斷矩陣

以重慶工商大學融智學院的五位教師的工作為例，利用層次分析法對其進行績效考評。

2.1 采取絕對評價法對被評估人員進行綜合評價

由學校督導組教師對被考核教師根據上述指標依據進行打分，每一項指標滿分為10分，其表格如下：

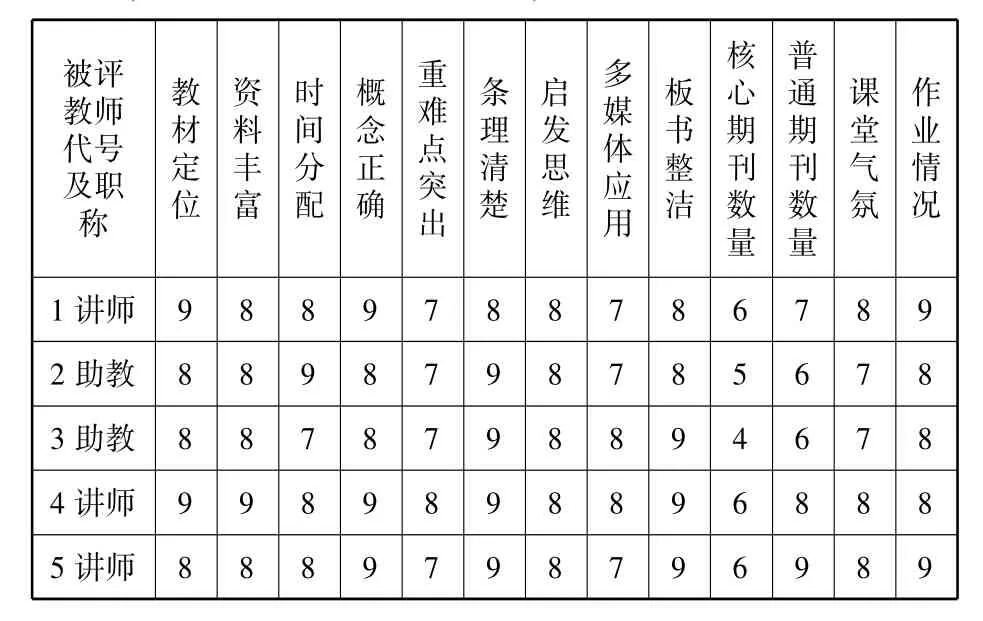
被評教師代號及職稱教材定位資料豐富時間分配概念正確重難點突出條理清楚啟發思維多媒體應用板書整潔核心期刊數量普通期刊數量課堂氣氛作業情況1講師9 8 8 9 7 8 8 7 8 6 7 8 9 2助教8 8 9 8 7 9 8 7 8 5 6 7 8 3助教8 8 7 8 7 9 8 8 9 4 6 7 8 4講師9 9 8 9 8 9 8 8 9 6 8 8 8 5講師8 8 8 9 7 9 8 7 9 6 9 8 9

打分專家職稱：（1）副教授、（2）副教授、（3）講師（重點）、（4）講師（重點）、（5）教授。

2.2 根據打分的情況進行綜合評分

為了避免主觀判斷明顯誤差， 首先將被評教師按職稱的高低進行分配，并且根據打分專家教師職稱的區別，將教授賦予45%、副教授賦予35%、講師（重點）賦予20%的比例進行分配，即得各項指標的數量評價，再計算綜合加權值，即：N=a×W，其中，N：表示績效考核的綜合評價分數；W：表示評分專家教師的權重；a：表示參評人員的權重。

2.3 建立判斷矩陣

根據所得的綜合測評分數， 針對其指標層中的每個指標，對考核教師進行作兩兩比較，如：對指標層中P1“教材定位”一項，比較五位教師中第i位和第j位，若第i位教師在“教材定位”方面其分數比第j位教師高2.5分，則記作aij=3，aij的取值如下表：

第i位比第j位教師分數差 0—1 2—3 4—5 6—7 8—9 1 3 5 7 9 aij

若兩位考核教師對某指標的表現介于上表中的兩者之間，則aij的取值為2、4、6、8。

由此，構造矩陣A1=（aij）5×5稱為判斷矩陣，同理，對P2“資料豐富”、P3“時間分配”、…、P13“作業情況”，對五位教師分別進行兩兩比較后，構造出的判斷矩陣依次為：

3.對判斷矩陣進行層次單排序并進行一致性檢驗

分別求出判斷矩陣A1、A2、A3、…、A13的最大特征值λ1、λ2、λ3、…、λ13及所對應的標準化的正特征值向量，W1、W2、W3、…、W13如下：

并且根據隨機一致性比值CR=CI/RI，對矩陣A1、A2、A3、…、A13分別進行一致性檢驗，發現矩陣A1、A2、A3、…、A13都具有滿意的一致性。

4.對五位教師進行優劣排序

該層次模型中的13項指標的權重分別為7%、7%、8%、7%、7%、7%、7%、7%、7%、10%、8%、9%、9%。

由13項指標的權重及所求的特征向量W1、W2、W3、…、W13，用向量表示為：7%·W1+7%·W2+8%·W3+…+9%·W13=（0.14180，0.16927，0.04192，0.54134，0.10567）T

由此可得到這五位教師績效考評的一個優劣排序為3、2、5、1、4。

5.結語

層次分析法所給出的這一排序方法，并不依賴于每位教師的評估成績，僅依賴于每一指標下教師兩兩比較的結果，利用層次分析法不但能夠選出參評教師最好的表現者，而且能夠對各位參評教師的績效表現排序，從定性到定量，給出每位教師得分的具體分值。

［1］和珍珍，劉秋靜，王超.層次分析法在評估中學課堂講課效果中的應用.［J］.科教文匯，2010（126）.50-51.

［2］李懿.應用層次分析法提高教學評估的科學性.［J］北京教育學院學報，1992（2）：43－48.

［3］王廋.實用計算機數學模型.［M］.安徽大學出版社，2003（2）：143-154.

［4］杜棟，龐慶華，吳炎.現代綜合評價方法與案例精選［M］.北京：清華大學出版社，2008：11-33.

［5］常少健，周文明，張磊.層次分析法在大學生畢業選擇中的應用［J］.四川理工學院學報（自然科學版），2007（1）：39-43.

［6］鐘強.層次分析法（AHP）在教師課堂教學評價中的應用［J］.聊城大學學報（自然科學版），2007（1）：98-100.

［7］王蓮芬.層次分析法引論［M］.北京：中國人民大學出版社，1990.