浙江省用水結構的組合預測*

胡玉琴、薛留根

（1浙江財經大學數學與統計學院/2北京工業大學應用數理學院，浙江杭州 310018/北京 100000）

浙江省用水結構的組合預測*

胡玉琴1、薛留根2

（1浙江財經大學數學與統計學院/2北京工業大學應用數理學院，浙江杭州 310018/北京 100000）

本文以浙江省用水結構為研究對象，在分別應用對數比變換和球面投影變換與灰色預測模型GM（1,1）結合的成分數據單一預測方法的基礎上，提出成分數據Aitchison距離最小化方法確定組合權重的組合預測方法，并對浙江省2013-2017年的用水結構進行預測。研究表明，組合預測能較好地提高預測的精度，增強預測的穩定性。

用水結構；成分數據；組合預測

一、引言

水資源作為人類賴以生存的自然資源，是國民經濟和社會發展的重要保障。隨著城市化進程的不斷推進，區域經濟增長需求與日益緊缺的水資源的矛盾凸顯。這一問題在經濟發達但人均水資源并不豐富的浙江省應該引起關注。用水結構作為水資源在區域生產生活各部門的分配結果，其結構特征直接反映水資源的可持續性發展狀況。因而研究浙江省的用水結構狀況并預測其發展趨勢，對于合理安排浙江省用水結構，實現水資源的合理配置，促進經濟發展有著重要的意義。

用水結構主要根據經濟活動進行分類，由農業用水、工業用水和生活用水組成。隨著人們對環境保護意識的提高，增加新的統計分類——生態用水。根據《中國統計年鑒》，浙江省自2003年開始對生態用水進行統計，用水結構由農業用水、工業用水、生活用水以及生態用水這四部分組成，具體數據見表1。2003-2012年浙江省的總用水量呈現出先升后降，之后逐漸趨于平穩的過程。總用水量從2003年的205.98億立方米上升到2008年的216.62億立方米，隨后下降到2009年的197.76億立方米，之后趨于平穩，在200億立方米左右。農業用水是浙江省用水比重最大的部分，但其比重總體呈現下降趨勢，由2003年的53.5%下降到2008的45.6%，2009年上升到49.2%，2010年開始緩慢下降至2012年的46.1%；工業用水比重是浙江省用水的第二大用水部分，總體變動比較平緩，從2003年的26.8%上升2007年的30.4%，2008-2012年在30%左右波動；生活用水比重呈現明顯的上升趨勢，由2003年的14.1%上升至2012年的21%；生態用水比重在2003-2007年間在6%左右浮動，2008年達到最高值9.5%，之后下降達到2012年的2.3%。

表1 浙江省2003-2012年用水結構

從數據結構來看，用水結構為成分數據(compositional data)，可用描述統計學中的餅圖來表示某一事物中各種成分所占的比重。用數學形式表達，p維成分數據x=(x1,x2,…,xp),其中xi>0,i=1,2,…,p,滿足x1+x2+…+xp=1。由于成分數據始終存在定和條件1的約束，單一對各成分進行預測會使得預測結果不滿足定和條件1，因而在研究中應對成分數據進行整體分析，運用成分數據統計方法進行研究[1-2]。

本文以浙江省的用水結構為研究對象，分別運用成分數據的對數比變換和球面坐標變換分析并預測用水結構，并提出組合預測方法提高用水結構預測的精度。

二、成分數據的單一預測

定和約束的存在使得成分數據各分量間存在完全多重相關性，對原始成分數據采取數據變換，突破定和條件約束，然后采用常規統計方法對變換后的數據進行預測，從而利用反變換公式預測原始成分數據是解決成分數據預測的主要思路。目前主要有對數比變換和球面投影坐標變換進行成分數據的單一預測。

（一）基于對數比變換的成分數據預測

對成分數據x=(x1,x2,…,xp)作對數比變換：

將p個線性相關的變量xi,i=1,2,…,p轉換成p-1個獨立并在(-∞,+∞)內取值yi,i=1,2,…,p-1。

利用常規統計方法對yi,i=1,2,…,p-1進行分析，然后根據反變換公式

得到對應xi,i=1,2,…,p的相應預測值，用表示。

（二）基于球面投影變換的成分數據預測

對成分數據x=(x1,x2,…,xp)首先作變換，此時z=(z1,z2,…,zp)分布在半徑為1的p維超球面上；然后將z=(z1,z2,…,zp)

從直角坐標系變換到球面坐標系中，得到z=(1,θ2,…,θp，即

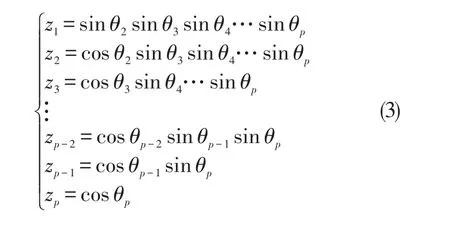
從而將p個線性相關變量轉換成p-1個獨立的轉角θi,i=2,3,…,p。

利用常規統計方法對θi,i=2,3,…,p進行分析然后根據反變換公式（4）式得到zi,i=1,2,…,p的預測值，從而根據xi=(zi)2得到xi,i=1,2,…,p的預測值，用表示。

（三）浙江省用水結構的單一預測

對表1中的數據進行對數比變換得到y1,y2,y和進行球面投影變換θ2,θ3,θ4，匯總見表2。根據散點圖，2008年作為異常值進行處理，因而剔除2008年數據。由于采取9年的數據，數據點較少采用灰色預測模型GM（1,1）分別對y1,y2,y3,θ2,θ3,θ進行預測。由表3，各個GM（1,1）模型的后驗差檢驗比C均小于0.35，表明預測精度等級均為好，模型具有較好的擬合效果和預測精度。

表2 對數比變換和球面投影變換數據表

表3 各個GM（1,1）模型的預測檢驗精度

根據各個GM（1,1）模型可得到2003-2012年（2008年除外）的擬合值BZ_8_525_553_558_589.png1,BZ_8_525_553_558_589.png2,BZ_8_525_553_558_589.png3，BZ_67_2031_2530_2056_2665.png2,BZ_67_2031_2530_2056_2665.png3,BZ_67_2031_2530_2056_2665.png4，根據相應反變換公式可得到2003-2012年（2008年除外）浙江省用水結構單一擬合值。表4中分別表示基于對數比變換與GM（1,1）方法下農業用水、工業用水、生活用水以及生態用水的擬合值。分別表示基于球面投影變換與GM（1,1）方法下農業用水、工業用水、生活用水以及生態用水的擬合值。由圖1可以看出基于對數比變換和球面投影變換的用水結構擬合值與真實值的擬合效果理想。

表4 浙江省用水結構的對數比變換和球面投影變換擬合值

圖1 對數比變換和球面投影變換的浙江省用水結構擬合圖

由于GM（1,1）適用于中短期預測，根據各個GM（1,1）模型得到2013-2017年的預測值1,2,y3，2,3,4，由相應反變換公式可以得到對2013-2017年未來五年的浙江省用水結構的單一預測。由表5，可以看到對數比變換和球面投影變換單一預測在生態用水比重上相一致，在農業用水和生活用水的預測趨勢上保持一致，但是球面投影變換變動幅度較小，對數比變換的變動幅度較大。在工業用水比重預測中，對數比變換預測趨勢下降，而球面投影變換預測趨勢則是上升。由于組合預測能夠充分利用單預測模型的信息，就有較高的適應能力，因而采取將對數比變換和球面投影變換預測的組合預測方法。

表5 浙江省用水結構2013-2017年的對數比變換和球面投影變換預測值

三、成分數據的組合預測

（一）Aitchison距離

由于受定和條件的約束，成分數據運算具有閉合性特點，因而成分數據的預測值與真實值之間的誤差，不能用歐幾里得空間的歐式距離度量，而應采用單形空間的Aitchison距離[7]進行度量。

Aitchison距離小，則預測精度高，反之，則預測精度低。

根據表4，分別計算2003-2012年（2008年除外）的用水結構的對數比變換擬合值xalr和球面投影變換擬合值xscr與真實成分數據x的Aitchison距離分為da(x,xalr)和da(x,xscr)。由表6的第二列和第三列可知，由于采取灰色預測模型GM（1,1）方法進行預測估計，兩種單一預測在2003年均沒有預測誤差，2006、2007、2009以及2011這4年的對數比變換預測精度高于球面投影變換，而2004、2005、2010以及2012這4年的球面投影變換預測精度高于對數比變換。兩種單一預測方法各有優缺點。

表6 對數比變換和球面投影變換的Aitchison距離

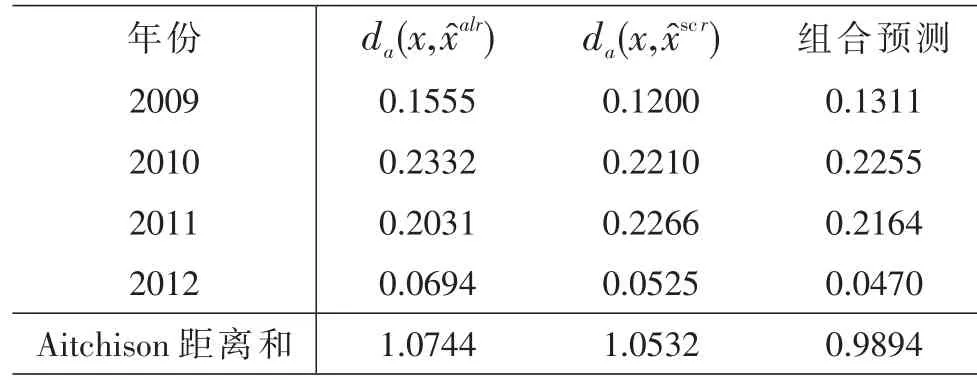
續表

（二）組合權重的確定

用對數比變換預測值xalr和球面投影變換預測值xscr的組合W1xalr+W2xscr（其中W1+W2=1,W1,W2≥0進行預測。關鍵是解決權重W1,W2的確定問題。

權重W1,W2應使得擬合值與真實值x的Aitchi son距離之和最小，可表示為

（三）浙江省用水結構的組合預測

根據表4和表5，分別對基于對數比變換和球面投影變換單一預測的擬合值和預測值用組合預測x*=0.385xalr+0.615xscr對浙江省用水結構進行分析，可得到表7。由圖2，可以看出組合預測具有較好的擬合效果，其精度高于單一預測。

表7 浙江省用水結構的組合預測

圖2 浙江省用水結構組合預測擬合圖

圖3 2013-2017年浙江省用水結構預測

用組合預測對浙江省2013-2017年用水結構進行預測，見表7和圖3，浙江省農業用水所占比重持續下降，從2013年的43.5%下降到2017年的32.8%，工業用水比重下降趨勢較緩，從2013年的31.2%下降到2017年的28.8%，生態用水則從2013年的1.4%下降到2017年的0.4%，生活用水比重則呈現顯著上升趨勢，從2013年23.5%，上升到2017年的38%，2017年超過農業用水，成為浙江省用水比重最大的部分。

四、小結

針對用水結構這一成分數據，本文首先分別運用成分數據對數比變換和球面投影變換與灰色預測模型GM（1,1）方法對浙江省2003-2012年的用水結構進行分析，分析表明，盡管對數比變換和球面投影變換預測能夠達到較好的擬合效果，但是單一預測的結果相差較大。為提高預測精度，本文運用組合預測方法，利用使得成分數據Aitchison距離最小來確定權重系數，得到較好的擬合精度和預測效果。

值得說明的是，本文用R軟件進行編程和分析，成分數據的Aitchison距離計算借助compositions包[8]來進行。

[1]Aitchison J.The Statistical Analysis of Compositional Data[M].London:Chapman and Hall,1986

[2]張堯庭.成分數據統計分析引論[M].北京:科學出版社,2000.

[3]王惠文,劉強.成分數據預測模型及其在中國產業結構趨勢分析中的應用[J].中外管理導報,2002(5):27-29.

[4]趙江濤,黃薇,王惠文.兩種成分數據預測建模方法的比較研究[J].北京航空航天大學學報:社會科學版,2003,16(2):37-40.

[5]施久玉,柴艷有.灰色成分數據模型在中國產業結構分析預測中的應用[J].統計與信息論壇,2007,22(1): 32-35

[6]張曉琴,陳佳佳,原靜.成分數據的組合預測[J].應用概率統計,2013,29(3):307-316.

[7]Aitchison J,Barceló-Vidal C,Martín-Fernández JA,Pawlowsky-Glahn V.Logratio Analysis and Compositional Distance[J].Math.Geol.2000,32(3),271-275.

[8]Gerald van den Boogaart KG,Tolosana-Delgado R. "compositions":a unified R package to analyze Compositional Data[J].Computers&Geosciences,2008,34(4),320-338.

（責任編輯：牛域寧）

*本文課題項目來源：全國統計科學研究計劃項目（2013LY103）、國家社科基金青年項目（13CTJ012）、國家社科基金項目（14BTJ031）、浙江省2014年度統計研究重點課題。