空間變換雙靶面成像系統圖像配準

畢齊林，王啟騰，全燕鳴

（1.廣東省自動化研究所，廣東 廣州 510070；2.華南理工大學機械與汽車工程學院，廣東 廣州 510640）

空間變換雙靶面成像系統圖像配準

畢齊林1，王啟騰2，全燕鳴2

（1.廣東省自動化研究所，廣東 廣州 510070；2.華南理工大學機械與汽車工程學院，廣東 廣州 510640）

針對熔池及熔池前區相連焊縫的雙靶面成像系統，采用特征基點標識及基于空間變換的方法，建立雙靶面成像系統的圖像配準模型。在圖像配準模型中應用最小二乘法確定配準模型中的參數，并通過實驗證明該方法能夠快速、準確地實現圖像配準并應用到實際的雙靶面成像系統中去，為實現焊接過程中熔池相對焊縫中心偏離量的監測創造條件。

特征基點；雙靶面成像；圖像配準；最小二乘；空間變換

0　引　言

大型構件角焊縫（fillet welding of corrugation of large structure，FWCLS）采用波紋側板與底板垂直的方式進行裝配，增強了箱型等結構的整體剛度，改善了力學性能。隨著鐵路運輸、航海、航空業等的快速發展，FWCLS得到了大量應用。然而FWCLS的波紋側板較薄、焊前剛性較差、制造過程也存在一定誤差，使得待焊裝配縫三維軌跡及縫寬無規律變化，難以實現高精密、智能化地焊接。針對這一問題，Quan等[1]提出了雙靶面成像系統的監測跟蹤方式，對焊接過程中焊槍軌跡及焊接工藝參數進行自適應調整。在雙靶面成像系統中，需要將兩幅圖像融合，才能實現焊槍軌跡的偏離及待焊裝配縫隙寬度變化的監測。然而，兩靶面的實際安裝位置與設計安裝位置存在偏差，故融合前需要對圖像進行配準，且配準的精度直接決定了FWCLS的識別準確度。

基于特征的圖像配準是目前使用、研究最多的圖像配準方法，它將對整個圖像的分析轉化為對圖像中某些特征的分析，大大提高了計算速度。Ward G[2]提出了一種平移變換的圖像配準模型，應用到同一場景不同曝光條件下的圖像配準問題中，實現系列圖像中高動態范圍的圖像融合，但該模型只能進行平移誤差的圖像配準，沒有考慮圖像間旋轉誤差的影響，存在一定的局限性。在此基礎上，為了實現航天器的實時多目標跟蹤和捕獲，柳祥等[3]提出了基于有效點的質心提取與消旋配準相結合的方法，利用消旋配準去除圖像間相對旋轉的干擾，解決了角度偏移帶來的影響。與此同時，譚勇等[4]引進了縮放參數，實現了遙感目標圖像的旋轉和縮放參數的高準確配準。隨著特征提取、特征匹配等技術的不斷發展，產生了很多基于特征的圖像配準方法[5-6]，從最初具有簡單平移關系的圖像配準到后來具有復雜變換（縮放、旋轉、灰度變換等）的圖像配準。

在雙靶面成像系統的圖像配準中，因目標的特征在兩幅圖像中存在鏡像關系，且對應的位置、圖像大小不同，導致傳統的圖像配準技術無法適用。目前，學者對于基于特征的圖像配準方法有深入的研究，其中最常見的模型是仿射變換模型[7]，該模型可以實現待配準圖像間存在的縮放、旋轉、剪切、平移的線性幾何關系的圖像配準，然而對于包含鏡像、平移、縮放的空間變換關系的圖像配準無能為力。因此，針對這種情況，基于特征基點標識及空間變換，建立了雙靶面成像系統的圖像配準模型，確定配準模型中的參數，在此基礎上結合實驗對配準模型進行誤差分析，為熔池相對待焊縫中心線的偏離量的在線監測提供了基礎條件。

1　雙靶面成像系統

在FWCLS的自動焊接過程中，為了提高圖像信息的利用率、改善計算準確度和可靠性，利于具有較大光強動態范圍的感興趣區的圖像監測，在同一時刻，雙靶面系統中的兩個相機在不同曝光條件下采集焊接過程中的圖像信號，將兩通道所采集到的感興趣的圖像特征（熔池和前區焊縫）進行處理，可以最大限度提取各通道中的有效信息，合成高質量的圖像，得到感興趣的參數。該雙靶面成像系統如圖1所示。

圖1　雙靶面成像裝置系統

該雙靶面成像系統包含相機安裝盒、兩個相機、半反半透鏡、濾光片、減光片、濾鏡等，如圖1（b）所示。首先，調整成像裝置的位置，使得物體反射的光線進入圖像獲取窗口，通過此處增加的濾波片，過濾掉部分波段的弧光干擾；然后，經過濾波后的光線到達半反半透鏡，一半光線直接透過，被相機1接收，另一半光線被半反半透鏡反射后，被相機2接收。在接收角焊縫焊接圖像的過程中，為了體現每個相機關注的側重點，并盡量使得其位于視場中心，在相機安裝座上設定了可調裝置，使得相機可以沿著成像裝置的橫軸、縱軸進行一定的調整。

2　雙靶面成像系統配準數模分析

在現場環境中，由于兩個相機、鏡頭、實際和設計的安裝位置、姿態存在差異，采集到的兩幅圖像也會存在偏差，不能采用簡單的平移法進行圖像配準。因此，針對該雙靶面成像系統的特點，在前人研究的基礎上，提出了一種采用基于特征基點標識及空間變換的方法建立兩幅圖像間的配準模型，將其變換到同一坐標系下，然后進行圖像融合，監測跟蹤熔池中心與焊縫中心線圖像的偏離量，實現焊槍軌跡偏離焊縫的在線監測。

2.1圖像配準模型分析

若定義S：Rn→Rn，且S（X）=T（X）+A，T是非奇異線性變換，A∈Rn，則變換S稱為空間變換。對于圖像配準問題，n一般取2或3，但對本文討論的數學模型，n可以取任意整數。由于噪音的存在，上述公式一般不可能精確成立。特征點集配準的目標是基于估計變換S，使得兩特征點集在某種意義上的誤差極小化，本文結合實際焊縫監測跟蹤的實際需求，主要討論基于二維空間的圖像配準，取n=2。空間變換具有平行線轉換成平行線、有限點映射到有限點的一般特性，平移、鏡像、縮放等是二維空間變換的特例。

1）平移：設坐標點（x，y）經平移Δx，Δy后的坐標為（x′，y′），則空間變換形式為

其中t=[Δx，Δy]T為平移矩陣。

2）鏡像：設點（x，y）關于直線ax+by+c=0的鏡像點為（x′，y′），則空間變換形式[8]為

其中：

為鏡像矩陣。

3）縮放：設坐標點（x，y）經比例因子k改變大小后的坐標為（x′，y′），則空間變換形式為

其中k為縮放系數。

綜合上述的空間變換形式可知，若一個點坐標經過平移、鏡像、縮放后的坐標可以用空間變換表示為

也可以簡化為

式中：p′（x′，y′）、p（x，y）——坐標矢量；

k——縮放變換因子；

R——鏡像矩陣；

t——平移矩陣。

2.2最小二乘參數估計求解

由Mallat等[9]的研究可知，如果兩特征點集與兩幅圖像之間對應關系是空間變換關系，且記pi′（xi′，yi′）為pi′，pi（xi，yi）為pi則：

需要解決的問題是求取圖像配準后標準差的極小值[10-11]：

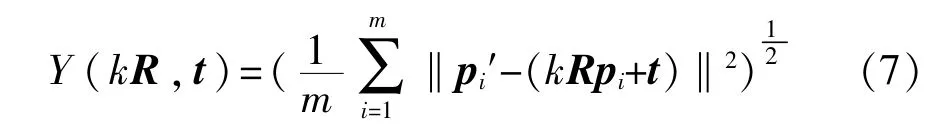
式（7）的空間變換參數為kR，t。若令：

E是元素全為1的m維列矢量，則：

即最小誤差函數可以簡化為以下形式：

式中TR[P]表示方陣P的跡，即是主對角線元素P之和。Y（kR，t）是關于kR和t的函數，因此極小化Y（kR，t）的（kR）*，t*應滿足下式：

由矩陣序的性質可知，對于任意m維列矢量S有

結合式（11），將式（9）代入到式（10）可得：

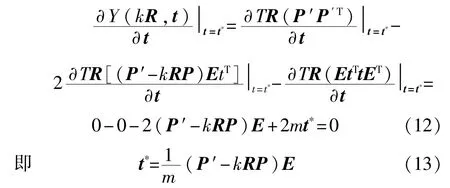
將其代入式（9）得：

由矩陣序的性質可知，對于任意m×m維矩陣Q=PJPT有：

結合式（15），將式（13）、式（14）代入到式（10）可得：

即

3　實驗過程與結果分析

為了通過式（13）、式（17）確定雙靶面成像系統中圖像配準的空間變換參數，結合真實的實驗環境，通過實驗對雙靶面成像系統圖像進行配準。

在實驗中采用同一型號的兩個相機和鏡頭，按圖1（b）所示安裝，依據該雙靶面成像裝置在實驗過程中的成像角度及與被監測目標體的位置關系，確定配準過程中成像裝置的拍攝位置。

3.1實驗過程

1）制作一個20×20的棋盤格標靶，在棋盤格中央做標記p1、p2、p4、p3，把該區域包含的格子的角點作為圖像配準的基準點（即64個基準點），如圖2所示。

2）安裝好該雙靶面成像系統，設置雙相機的參數，其中圖像大小為1600×1200，采集的圖像為8位灰度圖，獲取做好標記的標靶圖像，相機1和相機2分別獲取的圖像如圖2（b）、圖2（c）所示。

3）圖2（b）是待配準的圖像，圖2（c）是基準圖像，分別求出兩幅圖像中的64個基準點的圖像坐標，利用所述空間變換參數的最小二乘估計求解實現圖像配準。該求解過程在Matlab 2010中實現。

圖2　圖像配準

3.2實驗結果

通過Matlab編程，首先求得基準點的圖像坐標，然后利用空間變換參數的最小二乘估計求解，得到空間變換各參數。

鏡像、縮放變換矩陣：

平移矩陣：

配準后的結果如圖3所示。

3.3結果分析

分析對比圖3（a）中p1、p2、p4、p3中的方格的配準后角點坐標與圖2（c）基準圖像中p1、p2、p4、p3方格的基準角點坐標之間的位置關系，如圖3（b）所示。

從圖中可以看出，配準后的角點坐標與基準角點坐標大體一致，在x、y方向上的誤差保持在±2pixel內。其誤差主要來源于：雙靶面成像系統中兩個相機的中心軸在安裝的時候不是嚴格的垂直，獲取的圖像有一定的畸變；在求取待配準角點和基準角點坐標的過程中存在一定的誤差；空間變換參數的最小二乘估計求解是保證配準后的全部角點坐標最優，因此也會存在局部配準后的角點坐標誤差偏大的情況。總的來說，該模型的建立以及參數估計求解過程是比較準確的，并且具有良好的穩定性。

4　結束語

本文在各種圖像配準技術的基礎上，針對雙靶面成像系統的實際應用，建立了一種基于空間變換的雙靶面成像系統的圖像配準模型，在待配準和基準圖像中找到足夠多的特征點，利用最小二乘參數估計求得該空間變換的各參數矩陣，并通過實驗證明了該模型的正確性以及參數估計求解過程的準確性。

圖3　配準后的圖像及誤差分布

1）針對該雙靶面成像系統特點，提出了一種采用基于特征基點標識及空間變換的方法建立兩幅圖像間的配準模型。在此模型基礎上，利用最小二乘原理，求解該數學模型中的各參數矩陣。

2）通過實驗確定了該數學模型中的參數，并對配準結果誤差進行分析，在x、y方向上的誤差保持在±2pixel內，證明了該參數估計求解過程的準確性。

3）通過數學模型的建立及實驗，實現了具有平移、鏡像、縮放參數的雙靶面系統的圖像配準，為后期進行圖像融合，監測跟蹤熔池中心與焊縫中心線圖像的偏離量，實現焊槍軌跡偏離焊縫的在線監測提供了基礎。

[1]Quan Y M，Bi Q L.Image collection and processing system for welding pool and proximate seam using multiple image detectors[J].Computer Modeling and New Technologies，2014，18（11）：105-112.

[2]Ward G.Fast robust image registration for compositing high dynamic range photographs from handheld exposures[J].Joumal of Graphics Tools，2003，8（2）：17-30.

[3]柳祥，胡炳樑，邵秀娟.微型航天器多目標捕獲算法研究[J].宇航學報，2009，30（4）：1415-1420.

[4]譚勇，徐佩霞，徐守時.基于線形特征譜線的遙感目標圖像旋轉和縮放配準[J].中國科學技術大學學報，2010，40（8）：783-789.

[5]Harris C G，Stephens M J.A combined corner and edge detector[C]∥Proceedings of the Fourth Alvey Vision Conference Manchester，1988：147-151.

[6]熊興華，錢曾波，王任享.遺傳算法與最小二乘法相結合的遙感圖像子像素匹配[J].測繪學報，2001，30（1）：54-59.

[7]曾文鋒，李樹山.基于仿射變換模型的圖像配準中的平移、旋轉和縮放[J].紅外與激光工程，2001，30（1）：18-21.

[8]許社教.二維圖形的鏡像變換及其變換矩陣[J].西安電子科技大學學報，1994，21（1）：85-89.

[9]Mallat SG.Multifrequencychanneldecomposition of images and wavelet models[J].IEEE Trans Speech Signal rocessing，1989，37（12）：2091-2110.

[10]章權兵，羅斌，韋穗，等.基于仿射變換模型的圖像特征點集配準方法研究[J].中國圖象圖形學報，2003（10）：20-24.

[11]孔建，姚宜斌，許雙安.整體最小二乘求取坐標轉換參數[J].大地測量與地球動力學，2010，30（3）：74-78.

Image registration of double target surface imaging system based on spatial alternation

BI Qilin1，WANG Qiteng2，QUAN Yanming2
（1.Guangdong Institute of Automation，Guangzhou 510070，China；2.School of Mechanical and Automotive Engineering，South China University of Technology，Guangzhou 510640，China）

An image registration model has been developed for double target surface imaging system of molten pools and weld joints based on feature point identification and space transformation.Least squares were used to determine model parameters.Experiments show that the method can realize image registration in a swift and accurate manner and can be applied in actual double target surface imaging systems，thus providing conditions to monitor the deviation vector of molten pools relate to weld centers in welding processes.

basic characteristic points；double target surface imaging；image registration；least squares；spatial alternation

A

1674-5124（2015）12-0095-05

10.11857/j.issn.1674-5124.2015.12.024

2015-02-20；

2015-04-27

廣東省省院產學研項目（2013B091000006）

畢齊林（1983-），男，湖北黃岡市人，博士，主要從事機器視覺技術及應用研究。