小子樣測(cè)定葉片S-N曲線試驗(yàn)方法研究
張 冰,陳立偉,陳永祥,閆旭東,趙帥帥
(1.北京強(qiáng)度環(huán)境研究所,北京 100076;2.天津航天瑞萊科技有限公司,天津 300462)
小子樣測(cè)定葉片S-N曲線試驗(yàn)方法研究
張冰1,2,陳立偉1,陳永祥1,閆旭東2,趙帥帥2
(1.北京強(qiáng)度環(huán)境研究所,北京 100076;2.天津航天瑞萊科技有限公司,天津 300462)
根據(jù)試驗(yàn)要求,對(duì)葉片在樣本較少情況下測(cè)定其疲勞極限σ-1和S-N曲線。通過(guò)振動(dòng)疲勞試驗(yàn)的方法進(jìn)行研究,試驗(yàn)采用升降法選擇所施加振動(dòng)應(yīng)力的水平,采用異方差回歸分析方法進(jìn)行疲勞試驗(yàn)數(shù)據(jù)的分析。最后獲得葉片材料的均值S-N曲線和置信度為95%、可靠度為99.9%的P-S-N曲線,并得到各自曲線上的疲勞極限σ-1。此方法保證試驗(yàn)的順利進(jìn)行并且具有較高的可靠性,對(duì)于小樣本測(cè)定材料的S-N曲線具有較好的實(shí)用價(jià)值。
疲勞極限;小子樣測(cè)試;S-N曲線;升降法;異方差回歸分析方法
0 引 言
S-N曲線是反映材料的疲勞壽命和所承受的循環(huán)應(yīng)力之間關(guān)系的曲線。由于影響材料疲勞壽命的因素很多,其中許多因素都是隨機(jī)的,因此必須有不同程度可靠性的S-N曲線。通常以存活率P代表疲勞試驗(yàn)的可靠程度,作出不同存活率P時(shí)的S-N曲線,即P-S-N曲線。
目前測(cè)定S-N曲線一般是用一組試樣(取6~10根),在不同應(yīng)力Si下進(jìn)行疲勞試驗(yàn),測(cè)出其斷裂時(shí)的壽命Ni,得到一系列試驗(yàn)點(diǎn)后用光滑曲線連接而成的,這種方法測(cè)得的材料S-N曲線可靠性只有50%。P-S-N曲線通過(guò)數(shù)理統(tǒng)計(jì)方法處理疲勞試驗(yàn)數(shù)據(jù)得到,目前采用成組試驗(yàn)法,即要求在每個(gè)應(yīng)力水平下都做一組試件,然后分別求得各個(gè)應(yīng)力水平下的對(duì)數(shù)壽命均值、標(biāo)準(zhǔn)差和概率安全壽命,再通過(guò)曲線擬合得到P-S-N曲線,這樣就必須在每一個(gè)應(yīng)力水平上都保證有足夠多的試件,導(dǎo)致總的試件數(shù)量很大[1]。
結(jié)構(gòu)的疲勞壽命不僅與應(yīng)力水平有關(guān),還與平均應(yīng)力、應(yīng)力比、應(yīng)力集中系數(shù)和加載順序[2]有關(guān)。當(dāng)前國(guó)內(nèi)外學(xué)者研究重點(diǎn)也多放在確立各因素對(duì)疲勞壽命的影響關(guān)系上,S-N曲線的關(guān)系式也從兩參數(shù)模型不斷發(fā)展為更加準(zhǔn)確復(fù)雜的多參數(shù)模型[3-4]。本文重點(diǎn)介紹在實(shí)驗(yàn)室環(huán)境下,采用最為簡(jiǎn)單的兩參數(shù)模型設(shè)計(jì)試驗(yàn)流程,在小樣本情況下得到葉片材料具有較高可靠度的疲勞極限σ-1和S-N曲線。
1 S-N曲線兩參數(shù)模型
S-N曲線在雙對(duì)數(shù)坐標(biāo)下,可以近似表示為線性。有疲勞極限的S-N曲線,一般由傾斜部和水平部2部分組成,疲勞極限Nc為S-N曲線的轉(zhuǎn)折點(diǎn)。
基于兩參數(shù)應(yīng)力-壽命模型,S-N曲線傾斜部[5]可以表示為

式中:N——疲勞壽命;
S——應(yīng)力幅值;
m、C——材料常數(shù),與應(yīng)力比R和應(yīng)力集中系
數(shù)Kt等參數(shù)有關(guān)。
當(dāng)R=-1時(shí),結(jié)構(gòu)承受對(duì)稱交變應(yīng)力,其疲勞極限用σ-1表示。
對(duì)式(1)兩邊取對(duì)數(shù),得到線性方程式:
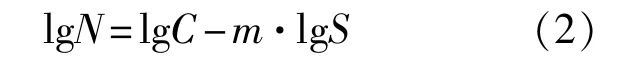
2 試驗(yàn)要求
試驗(yàn)對(duì)象是材料為TC17的發(fā)動(dòng)機(jī)葉片,數(shù)量為25片。TC17是美國(guó)研發(fā)的一種“富β”兩相鈦合金,其特點(diǎn)是強(qiáng)度高,淬透性好,適用于航空發(fā)動(dòng)機(jī)中風(fēng)扇及壓氣機(jī)的盤(pán)件。常溫下其抗拉強(qiáng)度σb為1 185 MPa,屈服強(qiáng)度σ0.2為1 144 MPa,彈性模量E為109GPa。
試驗(yàn)要求測(cè)得葉片對(duì)應(yīng)3×107循環(huán)次數(shù)的疲勞極限σ-1;測(cè)定疲勞極限σ-1后,在106~107循環(huán)、107循環(huán)附近分別補(bǔ)充2~3個(gè)應(yīng)力水平測(cè)定葉片的S-N曲線。
3 試驗(yàn)方法
3.1試驗(yàn)裝置及測(cè)試方法
振動(dòng)疲勞試驗(yàn)裝置為振動(dòng)臺(tái)。試驗(yàn)在葉片第一階彎曲振型對(duì)應(yīng)的共振頻率下進(jìn)行,試驗(yàn)環(huán)境溫度為室溫。
試驗(yàn)時(shí),葉片固定在夾具上,然后將夾具剛性固定在振動(dòng)臺(tái)上,振動(dòng)臺(tái)的運(yùn)動(dòng)部件帶動(dòng)夾具和葉片一起振動(dòng),振動(dòng)臺(tái)輸出固定頻率的正弦激勵(lì)信號(hào),激勵(lì)葉片進(jìn)行等頻率的正弦振動(dòng)。葉片上粘貼多個(gè)動(dòng)態(tài)應(yīng)變片,用來(lái)監(jiān)測(cè)葉片上各點(diǎn)的振動(dòng)應(yīng)力。
試驗(yàn)采用的控制方式是開(kāi)環(huán)控制,即振動(dòng)臺(tái)臺(tái)面上的加速度傳感器不參與控制,單純依靠改變控制儀輸出信號(hào)控制振動(dòng)臺(tái),其原理如圖1所示。具體方法如下:先固定振動(dòng)臺(tái)的激勵(lì)頻率,然后逐步增加控制儀輸出給功率放大器的驅(qū)動(dòng)電壓,使葉片上的最大振動(dòng)應(yīng)力達(dá)到要求的水平。試驗(yàn)過(guò)程中,由于最大應(yīng)力點(diǎn)處的形變較大,應(yīng)變片粘貼不穩(wěn)定,而低應(yīng)力水平點(diǎn)的應(yīng)變片可以長(zhǎng)時(shí)間正常使用,因此通過(guò)監(jiān)測(cè)較低應(yīng)力點(diǎn)的振動(dòng)應(yīng)力來(lái)保證最大應(yīng)力點(diǎn)的振動(dòng)應(yīng)力符合要求的方法是合理的。
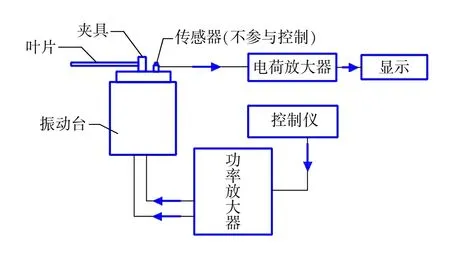
圖1 振動(dòng)臺(tái)系統(tǒng)開(kāi)環(huán)控制示意圖
3.2升降法確定試驗(yàn)應(yīng)力水平
疲勞極限定義為當(dāng)載荷循環(huán)數(shù)達(dá)到107次,試樣仍然不發(fā)生疲勞斷裂,此時(shí)對(duì)應(yīng)的最大應(yīng)力為材料的疲勞極限[6]。研究表明,材料疲勞極限σ-1與抗拉強(qiáng)度σb存在較好的相關(guān)性,在一定程度上可以用σb估算σ-1,并稱σ-1/σb為材料的疲勞比[7]。盡管這種簡(jiǎn)單估算方法的適用范圍有限,并且疲勞比的浮動(dòng)范圍稍大,但是這些研究提供了一個(gè)重要的信息,即材料的疲勞極限σ-1與抗拉強(qiáng)度σb存在著一定的關(guān)聯(lián),可以將其估算數(shù)據(jù)作為試件振動(dòng)疲勞試驗(yàn)的初始應(yīng)力值。本文葉片材料TC17在常溫下的抗拉強(qiáng)度σb為1185MPa,結(jié)合表1中鈦合金的疲勞比,可以確定葉片振動(dòng)疲勞試驗(yàn)的初始應(yīng)力水平為355.5~711MPa。
在振動(dòng)疲勞試驗(yàn)中,壽命(循環(huán)次數(shù))N很難控制,比較容易實(shí)現(xiàn)控制的為應(yīng)力水平S。在測(cè)定疲勞極限時(shí),針對(duì)樣本有限的情況如何選擇應(yīng)力水平才能更加有效地利用樣本疲勞數(shù)據(jù),國(guó)內(nèi)外學(xué)者均開(kāi)展了大量的研究[8]。本文采用的是升降法,即當(dāng)在某個(gè)應(yīng)力水平下出現(xiàn)了疲勞極限,此后的應(yīng)力以該應(yīng)力值作為起始應(yīng)力,以一固定步長(zhǎng)作為變量進(jìn)行增減,不斷變化應(yīng)力水平進(jìn)行疲勞試驗(yàn),它使應(yīng)力水平更加集中地分布在疲勞極限附近。如9號(hào)試驗(yàn)件在應(yīng)力為390MPa時(shí)出現(xiàn)折斷,步長(zhǎng)設(shè)為10MPa,則之后的疲勞試驗(yàn)應(yīng)力水平選擇具體過(guò)程如圖2所示。
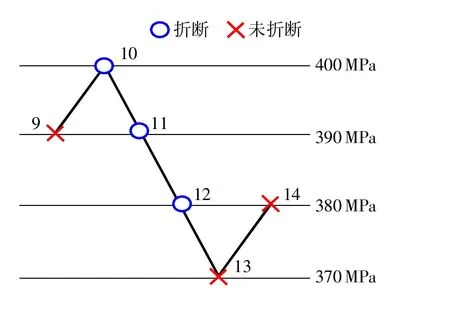
圖2 升降法試驗(yàn)
由于本試驗(yàn)要求對(duì)應(yīng)3×107循環(huán)的疲勞極限,因此在升降法中,對(duì)于107循環(huán)沒(méi)有斷裂的試樣,要求繼續(xù)加載至3×107循環(huán)后終止試驗(yàn)。
3.3小子樣測(cè)試的異方差回歸分析方法
異方差回歸分析理論,解決了工程上經(jīng)常遇到的方差不相等情況的性能曲線測(cè)試問(wèn)題。將該方法應(yīng)用于S-N曲線和P-S-N曲線的小子樣測(cè)試中,可以對(duì)S-N曲線和P-S-N曲線進(jìn)行散點(diǎn)測(cè)試,即每個(gè)應(yīng)力水平可以做一根試件,也可以做若干個(gè)試件,就能得到S-N曲線和P-S-N曲線,既可以節(jié)省大量試件,又能提高測(cè)試準(zhǔn)確度。該方法是將所有試驗(yàn)數(shù)據(jù)作為一個(gè)整體進(jìn)行統(tǒng)計(jì)分析,所以對(duì)第i個(gè)應(yīng)力水平下的均值壽命和概率安全壽命進(jìn)行估計(jì)時(shí),不僅利用該應(yīng)力水平下的ni個(gè)試驗(yàn)數(shù)據(jù),而且還利用其他應(yīng)力水平下試驗(yàn)數(shù)據(jù)提供的“橫向信息”[9]。
1)S-N曲線異方差回歸分析方法。大量試驗(yàn)數(shù)據(jù)已證實(shí),一般結(jié)構(gòu)的對(duì)數(shù)疲勞壽命服從正態(tài)分布,由式(2)可知,對(duì)數(shù)壽命y=lgN和對(duì)數(shù)應(yīng)力水平x=lgS之間存在如下關(guān)系:
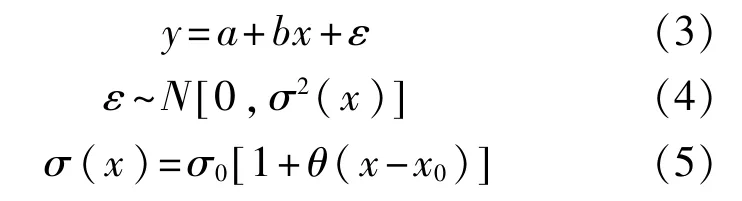
其中a=lgC,b=-m,σ0,θ均為待定參數(shù)。由式(5)可知,對(duì)數(shù)壽命y的標(biāo)準(zhǔn)差σ(x)隨對(duì)數(shù)應(yīng)力水平x線性變換,已不是常數(shù)。
根據(jù)異方差回歸分析方法求得參數(shù)a,b,σ0的估計(jì)量和則S-N曲線方程由下式給出:

標(biāo)準(zhǔn)差σ(x)的估計(jì)量為
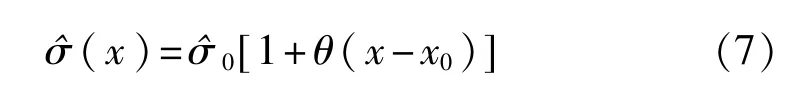
2)P-S-N曲線異方差回歸分析方法。由文獻(xiàn)[9]可知,置信水平為γ,存活率為p的P-S-N曲線由下式給出:

式中ap、bp為待定參數(shù)。
4 試驗(yàn)過(guò)程
4.1確定最大應(yīng)力點(diǎn)和試驗(yàn)應(yīng)力監(jiān)測(cè)點(diǎn)
1)選取某一葉片,在葉片的各個(gè)關(guān)鍵部位粘貼應(yīng)變片,如圖3所示。
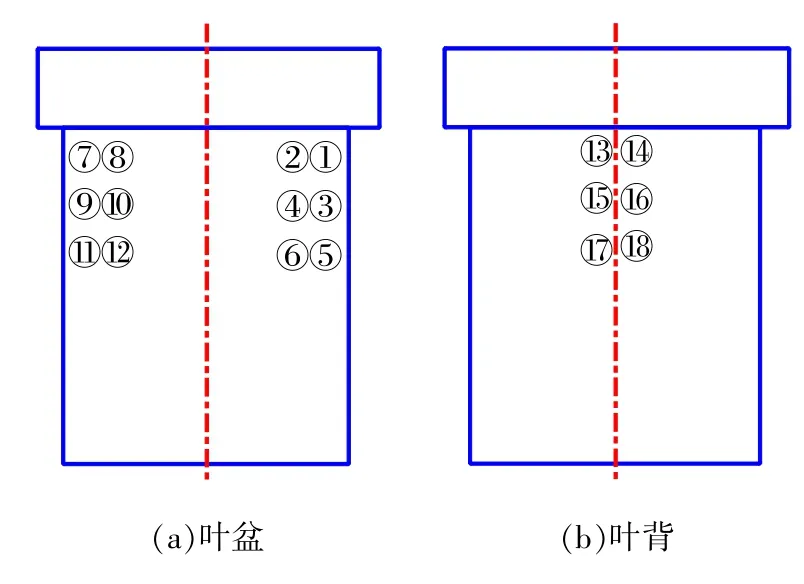
圖3 葉片關(guān)鍵部位應(yīng)變片分布
2)對(duì)葉片進(jìn)行正弦掃描振動(dòng)試驗(yàn)(共振頻率為109Hz),確定葉片的第一階彎曲共振頻率以及各監(jiān)測(cè)點(diǎn)的應(yīng)變分布情況,如表1所示。
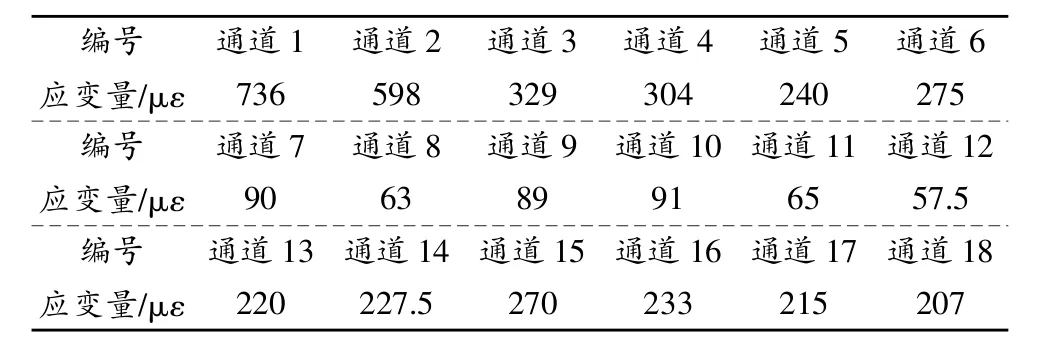
表1 葉片正弦掃描振動(dòng)試驗(yàn)數(shù)據(jù)
3)根據(jù)σ=ε·E,找出葉片在第一階彎曲共振頻率下應(yīng)力的最大點(diǎn)位置,為葉盆根部的①位置。
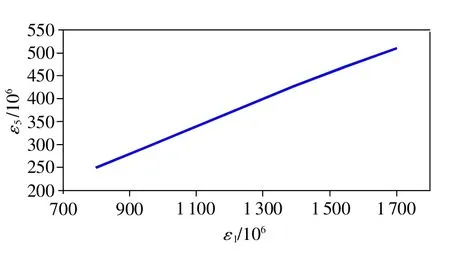
圖4 ①位置和⑤位置應(yīng)變關(guān)系曲線
4)通過(guò)不同量級(jí)下①位置和⑤位置應(yīng)變的比較,可見(jiàn)兩者基本符合線性關(guān)系,如圖4所示。因此選擇低應(yīng)力水平點(diǎn)⑤作為葉片振動(dòng)疲勞試驗(yàn)過(guò)程中的監(jiān)測(cè)點(diǎn),確保①位置應(yīng)力符合要求水平,并求得兩點(diǎn)應(yīng)力水平的比例系數(shù)k為3.26。
4.2確定振動(dòng)頻率
1)對(duì)每一葉片首先進(jìn)行正弦掃描振動(dòng)試驗(yàn),確定葉片的第一階彎曲共振頻率。
2)由于在振動(dòng)疲勞試驗(yàn)過(guò)程中,葉片的共振頻率會(huì)出現(xiàn)微小的左右偏移,造成葉片的振動(dòng)應(yīng)力起伏很大,難以控制,所以宜選取共振頻率附近的點(diǎn)作為激勵(lì)頻率,研究表明,選取共振峰后偏離0.5Hz的頻率點(diǎn)比較合適。
4.3確定振動(dòng)應(yīng)力
1)首先,根據(jù)材料的抗拉強(qiáng)度σb確定葉片疲勞試驗(yàn)的初始應(yīng)力水平S1=0.6σb≈710 MPa,記錄出現(xiàn)裂紋時(shí)的循環(huán)次數(shù)N1。
2)選擇第2個(gè)應(yīng)力水平為S2=0.3σb≈360MPa,記錄出現(xiàn)裂紋時(shí)的循環(huán)次數(shù)N2。
3)如果這兩個(gè)應(yīng)力水平下葉片出現(xiàn)裂紋時(shí)的循環(huán)次數(shù)均不能達(dá)到3×107,繼續(xù)降低應(yīng)力水平,直至出現(xiàn)在經(jīng)歷3×107循環(huán)后葉片不會(huì)出現(xiàn)裂紋的現(xiàn)象。
4)出現(xiàn)疲勞極限σ-1后,根據(jù)3.2所描述的升降法,以20MPa為步長(zhǎng),進(jìn)行不同應(yīng)力水平下的疲勞試驗(yàn),以葉片出現(xiàn)裂紋或者到達(dá)3×107循環(huán)為止。
4.4試驗(yàn)結(jié)束
1)升降法試驗(yàn),最高應(yīng)力水平以出現(xiàn)105壽命為止,最低應(yīng)力水平以出現(xiàn)3×107壽命為止。
2)最終試驗(yàn)以25片葉片全部完成疲勞試驗(yàn)為止,試驗(yàn)數(shù)據(jù)如表2所示。
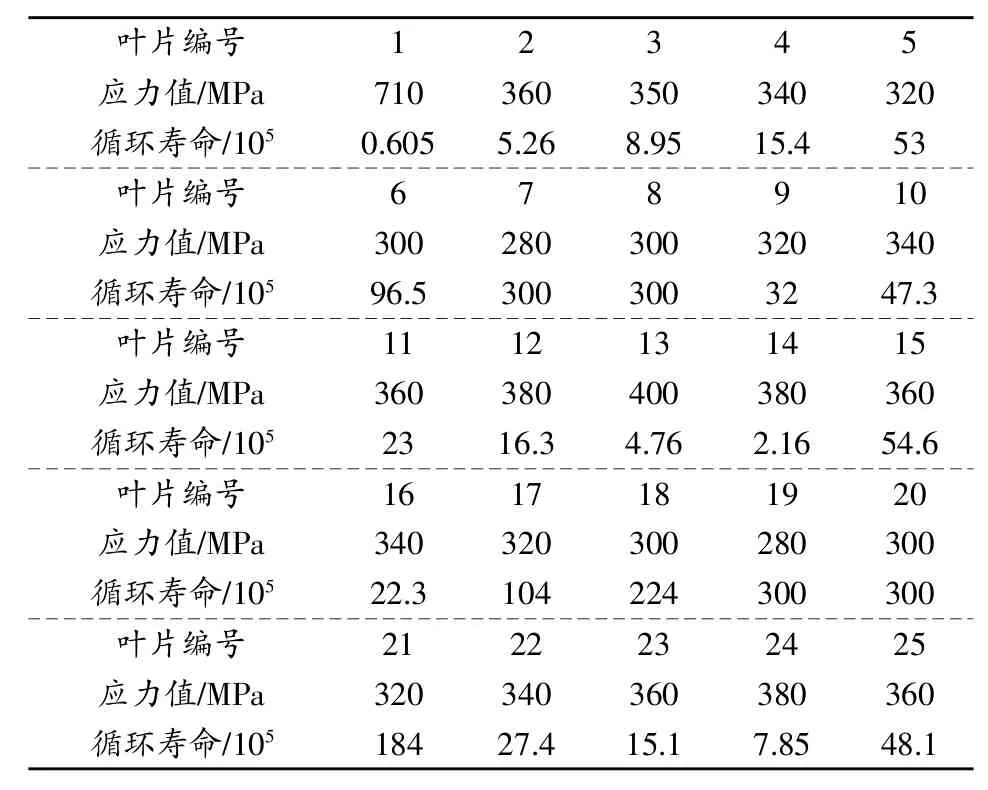
表2 葉片振動(dòng)疲勞試驗(yàn)數(shù)據(jù)
3)根據(jù)異方差回歸分析理論整理試驗(yàn)數(shù)據(jù),得出均值S-N曲線公式:
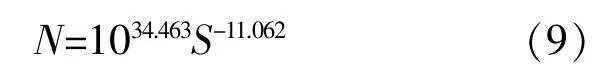
由式(9)可得,對(duì)應(yīng)3×107循環(huán)的均值疲勞極限σ-1為275.04MPa。
同樣可得到置信度為95%,可靠度為99.9%的P-S-N曲線公式:

由式(10)可得,對(duì)應(yīng)3×107循環(huán)的置信度為95%,可靠度為99.9%的疲勞極限σ-1為109.48MPa。
5 結(jié)束語(yǔ)
針對(duì)小子樣測(cè)定葉片的疲勞極限σ-1和S-N曲線,在葉片振動(dòng)疲勞試驗(yàn)過(guò)程中,采用升降法確定所施加振動(dòng)應(yīng)力的水平和采用異方差回歸分析方法進(jìn)行疲勞試驗(yàn)數(shù)據(jù)的分析;在試驗(yàn)控制方式和監(jiān)測(cè)方法方面,也確定了采用振動(dòng)臺(tái)開(kāi)環(huán)控制方式和通過(guò)監(jiān)測(cè)低應(yīng)力水平點(diǎn)來(lái)確保最大應(yīng)力點(diǎn)符合要求應(yīng)力水平的方法;最終確定了具體可行的試驗(yàn)過(guò)程。該研究方法的提出對(duì)于確定試驗(yàn)方案,保證試驗(yàn)順利實(shí)施并且具有高可靠度提供了必要的理論基礎(chǔ)。
[1]劉渭祈,李志潭.金屬材料的P-S-N曲線及其測(cè)定[J].太原重型機(jī)械學(xué)院學(xué)報(bào),1985,6(2):48-57.
[2]Nakajima M,Tokaji K,Itoga H,et al.Effect of loading condition on very high cycle fatigue behavior in a high strength steel[J].Int J Fatigue,2010(32):475-480.
[3]Sun C Q,Zhang X L,Xie J J,et al.A statistical analytical method for fatigue reliability containing veryhigh-cycle fatigue regime[C]∥Proceedings of ICAF,2013:91-94.
[4]馬少俊,胡本潤(rùn).金屬材料疲勞極限估算的多參數(shù)經(jīng)驗(yàn)公式[J].機(jī)械強(qiáng)度,2010,32(6):993-996.
[5]張繼旺,魯連濤.疲勞極限小樣本評(píng)估方法[J].哈爾濱工程大學(xué)學(xué)報(bào),2010,31(3):336-339.
[6]Pollak R D.Analysis of methods for determining high cycle fatigue strength of a material with invesigation of Ti-6Al-4V gigacycle fatigue behavior[D].Alabma:Air U-niversity,2005.
[7]趙少汴.抗疲勞設(shè)計(jì)[M].北京:機(jī)械工業(yè)出版社,1994:59-67.
[8]Nicholas T.Step loading for very high cycle fatigue. BlackwellScienceLtd.FatigueFractEngngMater Struct,2002(25):861-869.
[9]傅惠民,劉成瑞.S-N曲線和P-S-N曲線小子樣測(cè)試方法[J].機(jī)械強(qiáng)度,2006,28(4):552-555.
Studies on small sample test method for blade S-N curve
ZHANG Bing1,2,CHEN Liwei1,CHEN Yongxiang1,YAN Xudong2,ZHAO Shuaishuai2
(1.Beijing Institute of Structure and Environment Engineering,Beijing 100076,China;2.Tianjin Aero-space Relia Technology Co.,Ltd.,Tianjin 300462,China)
To determine the fatigue limit σ-1and S-N curve of blades with few small samples as the test requirements.Vibration fatigue test,that is,the level of vibration stress was fixed via up-down method and the test data was analyzed through variance regression.The S-N curve of mean value and P-S-N curve with 95%-confidence coefficient and 99.9%-reliability of blade materials have been obtained,so as the fatigue limit σ-1of each curve.The method ensures the smoothness and reliability of the test and has a guiding significance in determining the S-N curve of materials through small sample test.
fatigue limit;small sample test;S-N curve;the up and down method;the variance regression analysis method
A
1674-5124(2015)12-0124-04
10.11857/j.issn.1674-5124.2015.12.030
2015-03-05;
2015-04-11
張冰(1985-),男,工程師,碩士,主要從事強(qiáng)度、振動(dòng)和可靠性工作。

