淺談數學教學中教師對教材的加工改造

徐洪木

摘要：教材是教師教學用的材料，是專家編寫的，水平很高，但不一定是適合學生學習的材料。究其原因，從數學教材來看不外乎是結構嚴謹、語言科學準確，再加上里面的實例大多不為學生熟悉這三點。

關鍵詞：教材;教師;學生

中圖分類號：G632.0 ? ? 文獻標志碼：A ? ? 文章編號：1674-9324（2015）20-0233-02

教材是教師教學用的材料，是專家編寫的，水平很高，但不一定是適合學生學習的材料。究其原因，從數學教材來看不外乎是結構嚴謹、語言科學準確，再加上里面的實例大多不為學生熟悉這三點。教材改革之后雖然有所改觀，但這三點仍然是學生自己不便使用教材的原因。雖然不少學校自己設計學案，但由于水平較低、缺乏研究時間，也無法取代教材。面對這些，一些腳踏實地、不浮躁的教師在課堂上對教材的結構、語言進行加工改造，使學生易于接受。但是這些東西是上不了優質課的，因為評課者不是學生，不會打出高分，但是在教學中他們卻能獲得優異的教學成績。道理很簡單，語言是教學的傳遞工具，如何把教材中的知識用學生聽的懂的語言表達出來非常重要。除地域不同各有不同的語言特點外，初中學生能聽懂的語言的共同特點有三：①簡單。文字越少越好。②有趣。適合他們這個年齡段，最起碼他們熟悉。③宜淺不宜深。要做到這三點是很難的，也就是我們平常說的深入淺出。教學語言的這些應有的特點，評課者是無法覺察到的：第一，評課者不是學生;第二，他們大多數多年不教學生了。在這篇文章里，筆者以初中數學幾處知識點的教學處理方式和片段為例，談一下對教師教材的合理加工改造。

一種食材無論如何的營養豐富，都要經過廚師的多工序的料理才能成為美味。食材再有營養沒有了食客需要的色香味，也不能有效地發揮他的作用。數學教材對于學生就像充滿知識營養的食材，必須經過教師的加工才能被學生接受。現行的數學教材是凝聚了課改實驗的教育專家、學科專家、教研人員等一級一線教師的智慧，里面的科學性、知識性沒有必要去懷疑，但是不同教師用它教出了知識能力不同的學生，千差萬別。其中一個重要的原因就是不同的教師對教材做了不同的加工改造。下面從幾個方面談一下自己的看法。

一、對教材中符號的翻譯

教育要面向世界，教材里的各種符號都是國際通用的。除了一些學生必須掌握的數學符號，各種單位符號學生非常不適應。在初一應用題的教學中，這些符號成了不少學生的攔路虎。如：t表示噸，h表示小時，dm表示分米;更有一些合成單位，如：km/h表示千米/小時，t/hm 表示噸/公頃，這些使得學生感到陌生，從而影響對題意的理解。一些經驗不足的教師經常遇到這樣的事：一個感覺難度不大的例題學生卻說聽不懂。指導學生問“3h”是什么意思，才明白“小時”的符號影響了學生。再如找單項式 的系數時，學生找不出來，也不排除概念不清的原因。但往往解釋清楚兩點就行了：①π是數不是字母，②此單項式還可寫成 與a b相乘的形式：

其實這樣的事情在講解題目以前教師應該想到，提前解決。掃除這種簡易的障礙，使學生有精力學習相對重要的數學知識。

二、對教材中一些語句的科學合理的再加工

教材中的語句是嚴密科學的，但也有不通俗易懂的缺憾。對這些語句的再加工，使之變得易于被學生接受，這是我們教師的事。例如，教材中對方程的解是這樣定義的：“能使方程左右兩邊相等的未知數的值”。這句話雖然字少，但省略了主語，學生對此不好理解。教學中應依據實例演示，再去解釋為“一個數代替未知數計算后，如果等號兩邊的得數相等，那么這個數就是方程的解。”這樣學生就比較好理解了。再如教材對中心對稱性質的敘述，有一條是“對稱點所連線段經過對稱中心，而且被對稱中心平分。”在教學中，我把它改成了“對稱點是任何一對對稱點連線的中點，”作為輔助，簡潔明了便于識記。一個材料的優劣應看它是不是適合接受它的對象。照本宣科、生搬硬套不會有好的收獲。

三、引入實例要從學生身邊去找

照抄課本上的實例教學，會使學生有陌生感。如果遇到要解決一個學生不熟悉的實際問題時，可用一個具有相同數學意義的學生熟悉的實際問題來代替，而問題應盡量新奇，不落俗套。如把例題中的人名改成本班的學生姓名，把地名改成學校周圍的村鎮、車站等，這些都會增加學生的接受興趣，使得例子生動起來。在七年級方程應用問題中，商品買賣問題學生最難懂。售價、進價、利潤、利潤率四個量的關系搞得學生暈頭轉向。每次教學進行到這里我就重復一個虛構的實例：你1元錢買了一只雪糕（冬天就改成烤地瓜）1.5元賣給了你的同桌。你的進價是多少？（學生答1元）售價是多少？（學生答1.5元）賺了多少？也就是利潤是多少？（學生答0.5元）賺的錢與進價的比值是多少？也就是利潤率是多少？（學生答0.5或者說50%）在最初接觸這些量的關系時，這樣的例子使學生輕松欣喜，感覺到了利潤的產生，這個實例也為學生對此問題的理解起到了重要的作用。再看它們的關系式：售價-進價=利潤，利潤率=利潤/進價，這樣就不再陌生了。

四、對教材中的一些知識點的給出形式

教師在教學中要變化不同的表達方式，訓練學生多種思維習慣的形成，以提高學生的思維能力。

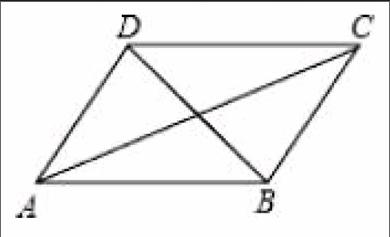
例如：除法法則：除以一個數等于乘以這個數的倒數。要出示式子：a÷b=a×1/b（b≠0）。而對于一元二次方程的求根公式x==Δ=b-4ac≥0因為數學符號多，在教學時，一定要讓學生在學會推導后，反復用語言敘述來幫助盡快熟記。在一些需要圖形而沒有圖形的問題中，一定讓學生畫出圖形。這樣一方面能培養學生的圖像思維，另一方面使問題中的內在規律形象直觀，便于學生解決問題。同時，在教學過程中要鼓勵學生學會發現教材內容中的關鍵語句，讓學生弄清每個教學用語的確切含義，掌握好數學符號的意義和使用方法，并且讓學生對于符號語言、圖形語言、文字語言進行相互轉化訓練。例如，在學習四邊形性質時，一條性質既要讓學生會用文字語言敘述，也要會用數學符號來表示，并能畫出圖形指出符號表示的具體位置。比如“平行四邊行的兩組對角相等”在推導證明后，再讓學生練習這樣表示“若四邊形ABCD是平行四邊形，則∠ABC=∠CDA，∠BAD=∠DCB。”并能指出在圖中的具體位置，出示的圖形不可過于簡單，最起碼要像下圖一樣有對角線。

說到這一點，不能不說函數，函數本身有三種變現形式：解析法、圖像法、列表法。在解決一個問題時，單純地一種表示很難讓學生明白。以二次函數為例，一個題目的出現本身也是在用不同方法表示的。

例如：（2005·浙江）根據下列表格的對應值，判斷方程ax +bx+c=0（a≠0，a、b、c為常數）一個解的范圍是（ ?）。

A.3

C.3.24

考點：用二次函數圖形求一元二次方程的近似值。

分析：根據函數y=ax +bx+c的圖像與x軸的交點就是方程ax +bx+c=0的根，再根據函數的增減性即可判斷方程ax +bx+c=0一個解的范圍。

解：函數y=ax +bx+c的圖像與x軸的交點就是方程ax +bx+c=0的根，函數y=ax +bx+c的圖像與x軸交點的縱坐標為0;由表中數據可知：y=0在y=-0.02與y=0.03之間，所以對應的x的值在3.24與3.25之間，即3.24

點評：掌握函數y=ax +bx+c的圖像與x軸的交點與方程ax +bx+c=0的根的關系是解決此題的關鍵所在。

以上題目用一種方法是無法表達和解答的。

當然在教學實踐中，數學教師要切實體會現代技術的使用，正確運用能幫助學生加深理解、豐富想象、減輕學習難度。但是利用現代技術對教材進行改造加工，主要是在課件的制作使用時還要注意：（1）課件必須依據學生的接受程度而設計，不是課件越玄妙越好，學生必須看得懂。如果課件播放形式過于復雜會影響學生對課件承載知識的掌握。如在教學有理數的大小比較時，用投影放出具體以正負數表示海拔高度的實例就很好，簡單明了，直觀形象，很容易理解和掌握;有的教師出示股票的變化圖像，而且還有動畫，理由是有利于激發學生的創造力。雖然在優質課評選和課件制作評選中會獲獎，但教學效果卻不會好。學生喜歡現代教育技術的媒體課件，好的課件會幫助學生掌握新知識，便于各種能力的提高。但教師也不能因學生的獵奇心理故意制作不利于知識傳播和能力培養的課件。（2）課件使用只能是讓學生認識規律，不能取代原始的訓練。一些基本圖形的畫法，演算過程的書寫都不能用課件代替。

教師和學生是教材的使用者，但學生是通過教師去使用教材的，因為學生駕馭不了教材。學生面對教材就像一個不會做飯的人面對一些上好的食材，何況有的學生還在懷疑教材對于他的意義。因此教師改造加工教材的作用意義是重大的。任何教育理論、教學方法、前輩專家的經驗借鑒都離不開教師面對的學生，也離不開教師工作的學校的位置和條件。