潤物無聲，論數學素養在教學中的培養
——以 《分數的初步認識》為例

◆華中師范大學教育學院 肖 敏 周東明

潤物無聲，論數學素養在教學中的培養
——以 《分數的初步認識》為例

◆華中師范大學教育學院 肖 敏 周東明

數學素養是每一個人都應該具備的基本素養，而數學素養的培養更是義務教育階段數學教育的重要目標。自“新課改”以來，許多一線老師都在作出努力和嘗試如何將數學素養的培養落實到具體的教學過程中。本文結合《分數的初步認識》這一內容來探討如何在教學設計中滲透數學思想和方法，培養學生的數學思維，以期培養學生的數學素養。

教學；數學素養；培養

讓學生獲得其所需要的基礎知識、基本技能、基本數學思想和基本活動經驗是義務教育階段數學教育的重要目標，而培養學生的符號意識、應用意識和創新意識亦是數學教育的重要內容。然而，如何有效地落實這些目標，則方法各異，其結果也是大相徑庭。筆者結合《分數的初步認識》的課程設計，旨在落實上述目標上做些探索，以期實現讓學生“運用數學思維方式進行思考”之目標。

一、找準起點，蓄勢待發

了解學生的已有認知基礎，才能于巧妙中讓學生從已知走向未知，再從未知走向已知，在不斷的認知沖突中運用數學思維去思考問題、感悟數學的思想與方法。

《分數的初步認識》是在學生已經掌握整數相關知識的基礎上來進行教學的，主要是讓學生理解幾分之一的真正含義。對于小學生而言，分數是除整數外的一個新數，是數概念的一次擴展。盡管分數是一個陌生和復雜的概念，但學生還是具備了一些與此相關的概念。一個是整數中“平均分”的概念認知，另一個就是生活經驗中的一些口語或抽象概念。如“一半”，學生知道將1個月餅平均分給兩個人，每個人得到一半，但是學生不知道這里的“一半”其實就是分數二分之一。有些學生可能已經知道“幾分之一”的表達，在生活經驗中也大致能體會到幾分之一的意義，但是這些理解都是比較膚淺的。這些知識經驗是學生學習分數的知識基礎，是教學的出發點。

此外，兒童的認知發展需遵循一定的規律。小學低年級兒童的認知發展更多的是通過動作和圖形學習來完成的，到了高年級才會逐漸抽象成符號和語言，即逐漸從形象思維向抽象思維發展。要使三年級學生接受“分數”這一新概念的認知，就必須遵循此年齡階段兒童認知發展的規律，即讓學生多動手操作，通過熟悉的生活經驗或具體形象圖形來認知抽象的分數概念。

二、定位終點，巧搭橋梁

義務教育階段的數學課程在繼續強調基礎知識和基本能力的同時，還強調通過有效的措施，使學生真正感悟和理解數學思想和方法，得到必要的數學思維訓練，獲得廣泛的數學活動經驗，體會思想方法的價值，從而提升學生的數學素養。

那么，如何在達成《分數的初步認識》知識目標的教學過程中巧妙地滲透數學思想和方法，讓學生得到思維的訓練，則需要教師用心去挖掘元素，設計橋梁。本節課的教學目標如下：

1.能結合具體的情境初步認識幾分之一，知道它的含義和各部分的名稱，能正確讀寫幾分之一這樣的分數。

2.能認識各種表征圖形或情境中的幾分之一，能用實際操作的結果表示幾分之一，并學會用直觀的方法去比較這類分數的大小。

3.通過動手操作、觀察和比較等數學活動來感知幾分之一這類分數的含義和意義，在動手與動腦的過程中發展動手能力和邏輯思維能力，培養符號意識、應用意識和創新意識，滲透極限和辯證的思想。

4.在分數的認識活動中感受分數的意義以及分數與生活的緊密聯系，從而進一步感受數學與生活的聯系以及加強對數學學習的興趣。

三、潤物無聲，重視過程

要實現讓學生“運用數學思維方式進行思考”的教學目標，必須重視教學過程。下面結合《分數的初步認識》教學過程的設計來具體說明。

1.找準支點，落實基本數學活動經驗

“基本活動經驗”是“四基”之一，學生基本活動經驗的獲得，要求教師必須結合數學教學內容，找準活動支點，適時適當適度地開展數學活動，累積活動經驗。本設計中的折疊正方形、運用數學符號、解決問題等活動過程，都是在積累學生的數學活動經驗。

在創設情境初步認識分數時，無論是教材還是優質課例，大都是用對折一個圓形物體的方式來導入。用圓來導入，其優點是對折起來比較簡便，但其缺點是思維方式單一、對折方式單一，活動經驗單一、對折結果單一。而本設計采用正方形導入，則思維多向、對折方式多樣、活動經驗豐富、所得結果多類。既培養了學生的思維和動手能力，又將培養學生的“基本活動經驗”落實到課堂的細節之中。

2.抓住機會，培養符號意識

符號意識是《義務教育數學課程標準（2011年版）》的10個“核心概念”之一，足見其在數學教育中的重要地位。然而，到底該如何培養學生的符號意識呢？除了教材中涉及具體的符號使用時必須不折不扣地完成教學內容外（如低年級時用“☆”這個圖形符號等），還必須結合學生所學的內容，不失時機地加強符號的滲透。例如，關于分數的表示，我們是這樣設計的：

師：除了分成4份、8份，我們還可以分成多少份呢？其中的一份又是它的幾分之一呢？

師：想象一下，如果是平均分成3份、5份、7份呢？你能夠說出每一份是它的多少嗎？

師：分得完嗎？

生：分不完。（老師接著板書 “……”）

師：那分成很多很多份，怎么表示呢？有誰幫幫老師？

（學生的表情十分豐富：好奇、疑惑、迷茫……）

師：我們可不可以用 “☆”來表示這個 “很多很多的份數”呢？比如表示成能不能這樣表示呢？（生討論）

其實是可以的。比如：當五角星表示的份數是100的時候，分數就是你還想到哪些符號呢？

師：你們學過哪些字母呢？想用哪個字母來表示？

（生回答）

師：其實，我們通常用字母 “n”來表示，它表示未知的份數，寫成可以具體為任何數（0除外）。（接著在省略號之后板書

師：大家看黑板，我們把數也數不完的像幾分之一這樣的數起一個名字，叫分數。（補充板書，呈現出：像這樣的數，都是分數）。我們還發現，（板書）把一個物體平均分成n份，其中一份就是它的

這樣的表示方法，既能夠將分數的表示方式“一般化”，使學生對分數的表示一步到位，又不會增加學生的學習難度。

3.深入挖掘，發展思維能力

注重引發學生的數學思考，讓學生學會獨立思考，體會數學的基本思想和思維方式，這是數學教育應該發揮的重要作用。

關于分數的表征方式，除了用面積模型和線段圖來表示，還結合分數的產生以及分數的意義引入了除法的運算結果、數軸和集合來表征分數，目的是讓學生體會從多種角度來思考問題，從而激發學生的思維，培養學生的思維方式。例如，設計了如下習題：

師：對于同樣的一個長方形，你們有的這樣折，有的那樣折。為什么折法不同卻都表示呢？大家可以討論一下。（展示學生的不同折法，如下圖）

生：都是一半、大小相等、都是一份……（教師可引導）

師：是的，折法不同沒有關系，只要是平均分成兩份，其中的一份就都是這個長方形的

同理，教師提問：有的用圓，有的用紙條，有的用長方形，為什么形狀都不一樣，也都可以表示呢？（展示學生的不同折法，如下圖）（學生討論思考）

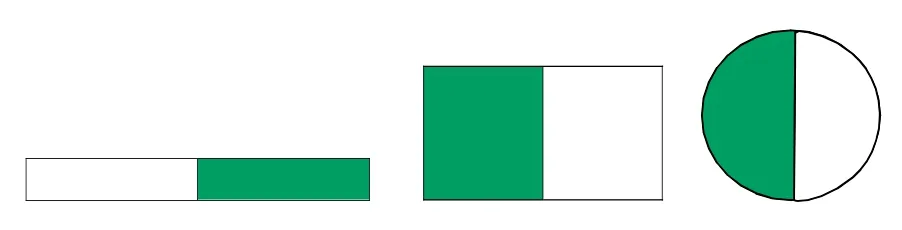
師總結（板書）：不管什么圖形，只要把一個物體平均分成2份，其中一份就是它的

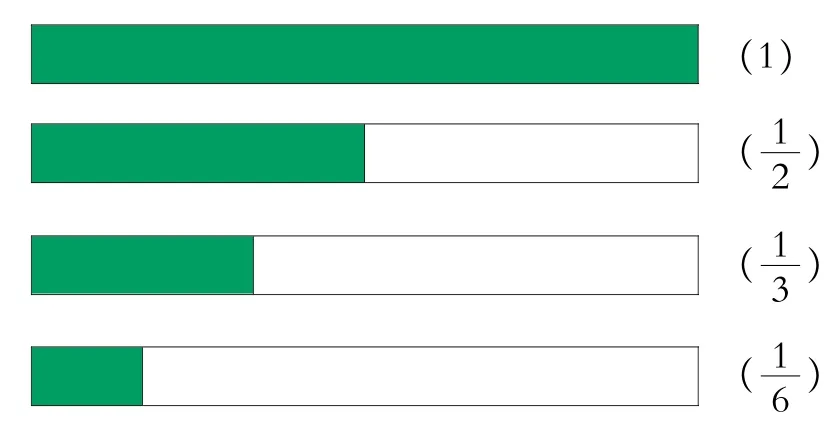
此外，關于分數的大小比較，本設計在用直觀圖直觀比較分數大小之后，又滲透了辨證的數學思想，讓學生從思維的角度來體會分數大小的比較。具體設計如下：

（生暢所欲言，回答不出來也沒關系。）

師：通過觀察，我們可以發現，對于這些分子為1的分數，當分母越大的時候，該分數越小。就像分一塊蛋糕，分的人數越多，每個人得到的蛋糕越少。同學們，只要善于觀察與總結，你們會發現更多數學的奧秘！

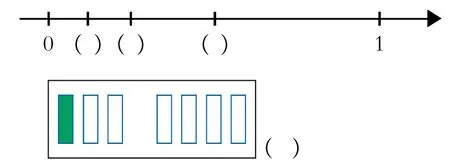
關于分數大小的估計，本設計也呈現了陰影部分逐漸變少的直觀圖，讓學生在直觀比較分數大小的基礎上來估算逐漸變小的分數，從而在無限變小的過程中初步感悟極限思想，即像幾分之一這樣逐漸變小的分數是有無數個的，且最小的那一個分數趨近于0。其直觀圖如下：要求學生估計出每一段長條中陰影部分的大小。

4.學以致用，培養應用意識

運用數學概念與原理去認識世界，從現實世界中抽象出數學問題并用數學方法予以解決，整個數學教育的過程都應該培養學生的應用意識和能力。本設計最后一道習題是讓學生通過測量來應用分數，旨在讓學生用數學思維去認識世界和解決現實世界中的實際問題，培養學生的應用意識，這正是適應了時代發展對人才培養的需求。同時，分數產生于測量，又運用于測量，經歷從生活走向數學，再從數學回歸生活的過程，可以讓學生體會到數學與生活的緊密聯系，感悟分數的價值，增強學生的應用意識。基于此，在教學過程的最后，設計了如下習題：

師：同學們，老師手中有和你們一樣長度的紙條（學具袋中的15cm長的紙條），但是老師沒有你們手中的正方形（邊長為5cm）。你們能用紙條量一量正方形的邊長并告訴老師嗎？老師也要做一個和你們一樣的正方形。

總之，讓學生獲得所需要的基礎知識、基本技能、基本數學思想和基本活動經驗是義務教育階段數學教育的重要目標，而培養學生的符號意識、應用意識和創新意識亦是數學教育的重要內容，這些都對數學素養的培養具有重要作用。如何在教學設計中滲透數學思想和方法，培養學生的數學思維，以期實現學生數學素養的培養，我們應該做到深入挖掘教材、剖析課程標準，在具體的教學內容中尋找培養的契機，在教學過程中讓學生運用數學思維去思考，從而達到潤物細無聲的效果。

（編輯：胡 璐）

肖敏，華中師范大學教育學院小學教育專業碩士研究生，曾獲得2015年度全國全日制教育碩士小學教育專業教學技能大賽決賽三等獎；周東明，現任華中師范大學教育學院教授、博士生導師，華中師范大學中小學數學教育研究中心主任，校級教學督導員，中國教育學會小學數學教學專業委員會理事、學術委員會委員，湖北省教育學會小學數學專業委員會副理事長、學術委員會主任。多年從事小學數學教學的研究工作，參與《實驗數學》研編，任《實驗數學教學文選》副主編，主編《小學數學新課程教學案例》、參編《小學數學教育概論》和《湖北考試史》，參與課題研究，承擔小學數學國家級骨干教師培訓工作等。

G623.5

A

1671-0568（2015）34-0074-04