“借題發(fā)揮”：讓開放題“睿智”走得更遠
——例談小學(xué)生開放題分析問題能力的培養(yǎng)

◆江蘇省鹽城市第二小學(xué) 袁文娟

“借題發(fā)揮”：讓開放題“睿智”走得更遠
——例談小學(xué)生開放題分析問題能力的培養(yǎng)

◆江蘇省鹽城市第二小學(xué) 袁文娟

數(shù)學(xué)教學(xué)要使學(xué)生獲得分析問題和解決問題的一些基本方法，增強分析和解決問題的能力，這些已然成為人們的共識。開放題具有條件開放、答案不唯一、解題策略多樣等特性，開展數(shù)學(xué)開放題專項練習(xí)，從培養(yǎng)審題習(xí)慣入手，逐步引導(dǎo)學(xué)生在面對問題時，能主動從數(shù)學(xué)的角度去分析和尋求解決問題的方法或策略。

開放題；分析問題；審題習(xí)慣；經(jīng)驗積累；策略指導(dǎo)

什么是數(shù)學(xué)問題分析呢？數(shù)學(xué)問題分析就是學(xué)生在新的情境狀態(tài)下，運用所掌握的數(shù)學(xué)知識經(jīng)驗，認識問題中的種種聯(lián)系，采用新的策略和方法，尋求問題答案的一種思維過程。

鑒于以上教育理念，筆者認為數(shù)學(xué)教學(xué)必須達成的目標之一就是：學(xué)生在面對問題時，能夠主動從數(shù)學(xué)的角度去分析和尋求解決問題的方法或策略，從而培養(yǎng)并發(fā)展學(xué)生分析問題的能力。調(diào)查表明，隨著小學(xué)課程的逐步深入，在質(zhì)量先行的教學(xué)背景下，教師往往設(shè)計過多、過密的專項練習(xí)，并希望通過如此“大劑量”的練習(xí)，讓學(xué)生掌握所謂的解題技巧。長此以往，勢必會造成部分學(xué)生“思維定式”，導(dǎo)致學(xué)生分析和解決問題的能力得不到發(fā)展，造成學(xué)生學(xué)習(xí)困難。為改善學(xué)習(xí)境況，保護學(xué)生的數(shù)學(xué)學(xué)習(xí)興趣，培養(yǎng)他們主動分析問題的習(xí)慣，在數(shù)學(xué)課堂上，筆者嘗試開展以培養(yǎng)學(xué)生分析問題能力為主要目的的專項開放題教學(xué)實踐。

一、借 “條件開放”，改善學(xué)生審題習(xí)慣

審題是分析和解決問題的前提，是對已知條件的全面認識，是學(xué)生將書面文字轉(zhuǎn)換為邏輯思維的過程。換言之，審題的好壞將直接影響后續(xù)的分析問題和解決問題。但是，在實際教學(xué)中我們發(fā)現(xiàn)，很多學(xué)生在解題的過程中往往過多關(guān)注已有經(jīng)驗，加上“想當然”的心理，不能夠仔細地審題，深入地分析題意，總按“老印象”辦事，導(dǎo)致錯題率居高不下。

在蘇教版四年級下冊（2014版）運算律教學(xué)單元中（如圖1），學(xué)生在解決含有兩個未知數(shù)的實際問題時，常有思考不全面或分析不到位的情況發(fā)生。原因在于：大部分學(xué)生在整理條件與問題時審題不清，在分析數(shù)量關(guān)系時糾結(jié)于原有經(jīng)驗和認識，或者不夠深入發(fā)掘題目中隱含的數(shù)量關(guān)系。筆者參照《小學(xué)數(shù)學(xué)開放題舉一反三（四年級）》第15講解決實際問題（條件開放），開展教學(xué)實踐。

筆者先以這樣的題型呈現(xiàn)（如圖2），并提問：讀題后，有什么要問的或者要說的？

生：老師，題目的條件是不是不全啊？用這個條件只能算小明語文和數(shù)學(xué)的總分吧？

一語嘩然，他的話頓時把全班學(xué)生的興趣都激發(fā)起來，紛紛小聲嘀咕：就是，只有一個條件怎么能分別求出語文和數(shù)學(xué)的成績呢？只能算兩門的總分！

原題：

圖1

課堂呈現(xiàn)：

圖2

師：想想辦法，怎樣才能把這題的問題解決呢？

生：再加上個條件，應(yīng)該就能求出來！

師：你們覺得他的建議可行嗎？

生：我也覺得要加個條件才行！

看著同學(xué)們紛紛點頭，筆者適時將題目完整呈現(xiàn)（如圖3）。

圖3

這節(jié)課筆者選用的“條件開放式”開放題，旨在打破常規(guī)的解決實際問題練習(xí)方式，以條件信息的“殘缺”促使學(xué)生產(chǎn)生分析問題的需要，再引導(dǎo)學(xué)生快速將條件信息和目標信息從問題情境中分離出來，從而促使學(xué)生養(yǎng)成全面、準確提取問題的條件信息和目標信息的審題習(xí)慣。長此以往，學(xué)生主動觀察、分析、思考問題的習(xí)慣會有很大改善，審題能力也會逐步增強。

二、巧 “化實為虛”，幫助學(xué)生積累經(jīng)驗

這里的“實”指的是為求答案的“標準”，學(xué)生缺少思維探索的時間和空間，只是死記公式、硬背數(shù)量關(guān)系的“模板”等等。“虛”指的就是：通過設(shè)置開放式的問題情境，助推學(xué)生打破原有的思維模式，充分調(diào)動自己的知識儲備，展開廣泛的聯(lián)想，從多方面、多角度對問題進行分析和思考。

如上述案例中“條件開放”的實際問題。筆者問學(xué)生：你覺得可以加個什么條件？

學(xué)生因知識儲備不同，所提條件也五花八門。具代表性的有：

生1：語文比數(shù)學(xué)多20分。

生2：語文和數(shù)學(xué)的分數(shù)同樣多。

生3：語文的分數(shù)是數(shù)學(xué)的2倍。

到這兒，筆者并沒有急于讓學(xué)生解決問題，而是繼續(xù)引導(dǎo)學(xué)生對所提條件再分析。問：這些添加的條件有什么特點嗎？

生1：好像都是語文比數(shù)學(xué)多一些。

生2：有一種是語文和數(shù)學(xué)比，一種是語文分數(shù)是數(shù)學(xué)的幾倍。

生3：我覺得都是語文分數(shù)和數(shù)學(xué)分數(shù)在比較。

筆者看準機會，問：這樣的條件信息實際上就是要讓我們發(fā)現(xiàn)語文分數(shù)和和數(shù)學(xué)分數(shù)之間……

學(xué)生恍然大悟：要知道它們之間是什么樣的關(guān)系！

筆者趁熱打鐵：遇到問題時，一定要先進行認真分析，找出解決問題的關(guān)鍵信息，可不能滿足于單一的解題思路。

解答這道題的關(guān)鍵是發(fā)現(xiàn)實際問題中隱含的數(shù)量關(guān)系。不同的學(xué)生有著不同的思維特點和思維水平，“條件開放式”開放題具有的不完備性，使每一層次的學(xué)生都能展現(xiàn)自己分析數(shù)量關(guān)系的方法；答案的不唯一又能誘使學(xué)生主動與他人的方法進行比較，完善自己的解題思路。我們要始終堅持在教學(xué)中給學(xué)生創(chuàng)造提問、思考、判斷、探究和釋疑的機會，幫助學(xué)生在數(shù)學(xué)活動的探究中逐步累積分析問題的經(jīng)驗，讓數(shù)學(xué)思維的火花漸成燎原之勢。

三、重 “策略指導(dǎo)”，建構(gòu)個性解題模型

解決問題的價值不只是獲得具體問題的解，其重要的一點在于使學(xué)生學(xué)習(xí)一些分析問題和解決問題的基本策略。我們在教學(xué)活動中，要重視學(xué)生解決問題策略的指導(dǎo)，讓運用策略成為學(xué)生分析和解決問題的“一根手杖”。

開放題的解題策略是非常規(guī)的，沒有固定的、現(xiàn)成的模式可以遵循，既往的那種依靠死記硬背、機械模仿式的經(jīng)驗是找不到問題的出路的。借助這樣的特性，引導(dǎo)和鼓勵學(xué)生主動使用分析策略，拓寬解題思路。

1.畫圖表征，問題分析形象化

以《小學(xué)數(shù)學(xué)開放題舉一反三（二年級）》第7講為例。

例：明明家、紅紅家和學(xué)校同在一條筆直的馬路上，從明明家到學(xué)校要走2000米，從紅紅家到學(xué)校要走3000米，那從明明家到紅紅家要走多少米？

讀題、思考后，師問：你的想法怎樣表達更容易被大家接受？

低年級學(xué)生的思維還是以直觀思維為主，當他發(fā)現(xiàn)已經(jīng)不能用算式來表達自己的想法時，會轉(zhuǎn)而尋找更直接的方法——圖畫。（如圖4）

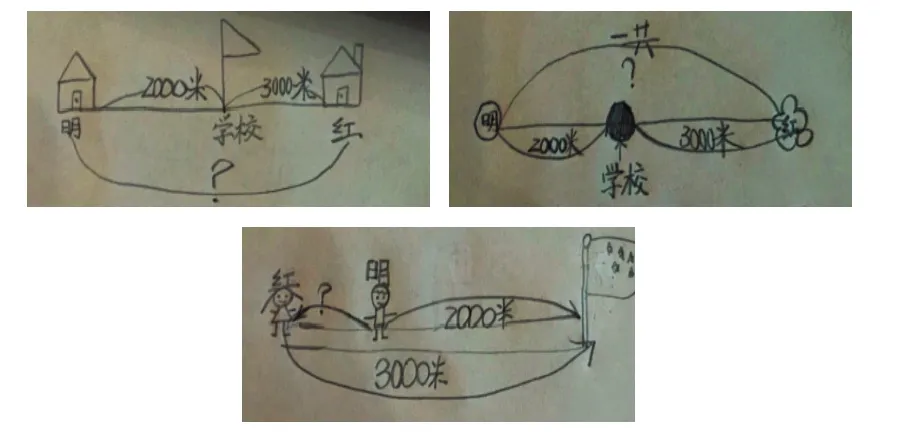
圖4

可能學(xué)生在畫圖時，并不能把兩種情況都表達出來，但是當自己的想法與別人的想法發(fā)生碰撞時，一道復(fù)雜多解題也就迎刃而解了。所以特別強調(diào)的是，要從低年級開始就鼓勵孩子用圖表征問題，讓畫圖成為學(xué)生分析問題的有力手段。

2.列舉嘗試，問題分析有序化

列舉也是一種重要的分析問題的策略。以《小學(xué)數(shù)學(xué)開放題舉一反三（四年級）》第13講為例。

例：王師傅打算用24厘米長的籬笆圍一塊長方形的菜地（長和寬都是整厘米數(shù)）。它可以怎么圍？圍成的菜地的面積是多少平方米？

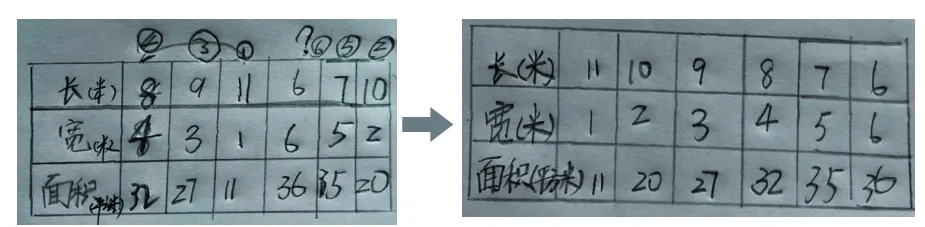
這個問題具有很強的開放性，筆者首先引導(dǎo)學(xué)生討論：你想圍的菜地的長和寬是多少？討論、交流中，學(xué)生發(fā)現(xiàn)需要描述的情況較多，自然喚起學(xué)生列表分析的需要。在不斷地嘗試、不斷地調(diào)整自己的思考方向后，學(xué)生最終找出規(guī)律，體會了有序分析問題的價值。

3.情境模擬，問題分析生動化

在解決問題的過程中，對于一些較復(fù)雜或難以理解的問題，可以用人或物模擬問題的情境，通過實物操作或動態(tài)模擬，使語言敘述的問題變得生動具體，幫助學(xué)生理解和思考問題。

以《小學(xué)數(shù)學(xué)開放題舉一反三（五年級）》第27講為例。

例：一輛客車和一輛貨車同時從相距460米的甲、乙兩地出發(fā)，客車每小時行55千米，貨車每小時行45千米。3小時后，兩車可能相距多少米？

題目并沒有說明客車和貨車的行駛方向，即存在“相向”“背向”“同向”3種可能，屬于答案不唯一的發(fā)散性開放題。教學(xué)時，40%的學(xué)生傾向于畫圖，60%的學(xué)生希望能走一走，感受這3種可能。筆者讓部分學(xué)生沿著既定的路線感知這3種可能，部分學(xué)生通過觀察，將看到的模擬情景用圖表示出來，“合二為一”直觀、生動地幫助學(xué)生分析問題、理清思路。

需要指出的是：分析問題使用的這些策略并不是互相割裂的，在實際操作中，這些策略往往是結(jié)合在一起使用的。教師要經(jīng)常開展“典型開放題”教學(xué)實踐，鼓勵學(xué)生針對具體問題合理運用分析策略，并適時將學(xué)生使用的策略“放大化”“顯性化”。

總之，這樣的開放型專項練習(xí)課，通過多角度地討論和辯論，使學(xué)生感受套用舊經(jīng)驗、沿用老模式的弊端，體會分析問題的重要性；通過多層次地嘗試和運用，使學(xué)生積累了分析問題的經(jīng)驗，強化了分析問題的能力，獲得了一些解決問題的有效策略。我們相信，堅持這樣的開放題教學(xué)，一定能有效訓(xùn)練學(xué)生的數(shù)學(xué)思維，提高學(xué)生的數(shù)學(xué)素養(yǎng)！

[1]義務(wù)教育數(shù)學(xué)課程標準[M].北京：北京師范大學(xué)出版集團. 2011.

[2]戴再平等.數(shù)學(xué)開放題研究[M].廣西：廣西教育出版社.2012.

[3]楊傳岡等.小學(xué)數(shù)學(xué)開放題舉一反三[M].南京：南京大學(xué)出版社.2014.

[4]張丹.小學(xué)數(shù)學(xué)教學(xué)策略[M].北京：北京師范大學(xué)出版集團. 2010.

（組稿：楊傳岡 編輯：胡 璐）

袁文娟，中共黨員，江蘇省鹽城市小學(xué)數(shù)學(xué)教壇新秀。曾多次在市、區(qū)各級課堂教學(xué)、基本功競賽中獲獎，主持和參與多項省、市級課題研究，有多篇論文發(fā)表，曾先后被評為鹽都區(qū)優(yōu)秀共產(chǎn)黨員、優(yōu)秀少先隊輔導(dǎo)員等榮譽稱號。

本文系全國教育科學(xué)“十二五”規(guī)劃教育部重點課題“數(shù)學(xué)開放題對小學(xué)生思維發(fā)展的具體影響評測”研究成果，項目編號：DHA140327。

G623.5

A

1671-0568（2015）34-0094-03