城市復雜交通網絡道路重要性評估方法

張喜平，李永樹，劉 剛，王 蕾

（1.西南交通大學地球科學與環境工程學院，成都610031；2.重慶郵電大學軟件學院，重慶400065）

0 引言

城市路網是支撐城市區域經濟和城市發展的重要基礎設施。路網由許多不同的路段組成，各個路段在整個路網中所處的地理位置和承擔的交通流量是不一樣的，因此各個路段的重要性也有所不同。在路網中選取重要的路段對路網結構穩定性和控制有效性具有重要的意義。道路重要性的評估首要解決的問題是道路網絡中路段的拓撲關系識別。GIS城市路網拓撲關系的表達有兩種方式：原有拓撲與對偶拓撲結構［1－3］。在廣義拓撲分析方法中，對偶圖因具有拓撲關系識別簡單、更能識別線路的交通特性、更符合實際交通運行特征等優勢而多用于GIS的路網表達中。

目前復雜網絡理論逐步應用在交通網絡領域，已有很多交通網絡被證實滿足復雜網絡特性。例如Porta等［4］應用復雜網絡理論對比分析了6種具有不同結構的城市道路網絡，高自友等［5］從多個角度提出復雜網絡在交通領域的應用前景。各國的學者利用復雜網絡理論展開了其網絡節點重要性評估的研究。在路網道路重要性評估中，文獻［6］提出了一種基于路段選擇概率的路段重要性評估方法，該方法在考慮出行者對出行時間的感知誤差的前提下，利用算法求出各個路段的選擇概率，選擇概率越大，路段越重要；文獻［7］中提到了瑞典的學者Erik Jenalius等人提出的一種路段重要性評估算法，該方法是路網中，假設路段上已發生使路段降級甚至失效的事件，對路段失效后的后果進行計算，從而根據它確定路段的重要性；文獻［8］提出了一種基于路段可靠性評價的方法用于確定路網中路段的相對重要性評估；文獻［9］利用網絡的連通性來反映路網中路段節點的重要性。文獻［10］提出了基于場論的復雜網絡節點重要性的評估方法，該方法主要計算了節點的拓撲勢，根據拓撲勢的計算結果決定節點的重要性，該方法考慮了復雜網絡中節點的相互作用。

文獻［4－9］采用直接度量或間接度量的方式去評估路段的重要性。該類研究方法雖對路網中路段重要性的評估具有一定的有效性，但對路網的流量分配要么使用最短路由的方法，要么使用用戶均衡配流的方法。最短路由算法的配流方式多數以節點的介數作為節點流量的反應，這種方法通常不能真實反應節點所承載的負載量，而且介數不能體現交通擁塞對路由的影響。用戶均衡配流的方法雖然能動態反應交通流量的變化，但其計算的時候通常采用一個阻抗函數作為求解的關鍵，該阻抗函數沒有考慮節點間流量的相互影響，即假設每個節點的阻抗僅僅是該節點流量的函數。文獻［10］從場論的角度提出一種復雜網絡節點重要性的評估方法雖然考慮了節點間的相互作用，但沒有用在交通路網中，不能體現路段的擁堵對其它路段的相互影響。

基于以上分析，本文在城市道路網絡對偶圖模型的基礎上，提出一種基于引力場的節點重要性評估方法。該方法下，采用基于引力場的路由方法［11］進行路網的動態配流，對路段的擁堵影響定義節點的引力場，考慮了路段的擁堵影響不僅僅是由相鄰路段引起的，還與相距很遠的節點發生擁堵相關，并且這種影響會隨著距離該路段節點的距離的增加而呈現衰減趨勢。基于這種考慮，本文引入了路段節點的m階鄰居節點的概念，并用于引力場的計算中，根據節點的引力場的大小來確定路段的重要性。

1 引力場論復雜網絡節點重要度評估方法

1.1 理論基礎

定義1 路網對偶圖［12－14］。建立基于廣義路網拓撲的對偶圖對偶拓撲方法是將道路按路名映射為節點、交叉口映射為邊。設G＝ ｛ V ， L｝是基于廣義路網拓撲建立的對偶圖，其中V是網絡中所有節點的集合，L為網絡中所有邊的集合。圖1為路網拓撲圖。

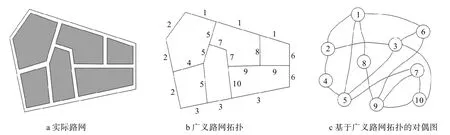
圖1 路網拓撲［3］Fig.1 The road network topology

定義2 節點度值是指節點直接相連的邊的數量，記為D。目前普遍認為節點的度值可以直接反映節點的重要程度。節點的度值越高，則說明該節點越重要。

定義3 m階鄰居節點。對于復雜網絡G＝ ｛ V ， L｝中任意節點i（i∈V），其1階鄰居節點為與節點i之間距離為1的節點，該類節點構成的集合稱作節點i的1階鄰居節點集，記為π（1）（i）；同理，則與節點i之間距離為2的節點為2階鄰居節點，其構成的集合稱作節點i的2階鄰居節點集，記為π（2）（i）；如此類推，則與節點i之間距離為m的節點稱為m階鄰居節點，其構成的集合稱作節點i的m階鄰居節點集，記為π（m）（i）。

1.2 路網節點的引力場計算

1.2.1 節點間引力的計算

天體物理學家J.Q.Stewart研究了Newton的萬有引力公式，提出了引力模型［15］。對于許多現實復雜系統，利用引力場理論研究其內部各組分之間的相互作用有助于進一步理解復雜系統的功能與結構特性，或許能發現一些重要的動力學現象。文獻［11］利用節點的引力場計算，定義了節點的引力場與節點的數據傳輸能力成正比，與節點間的距離成反比。通過以上定義我們發現：復雜交通網絡中節點的重要性與節點的數據傳輸能力、節點的距離、節點的度都有密切聯系［16－20］。文獻［11］定義的節點與數據包之間的引力考慮了復雜交通流量網絡中節點的距離，節點的數據傳輸能力的因素，因此這種定義可以引入到交通網路中對節點重要度的評估。根據復雜交通網絡中交通流量的特性，節點對之間的相互作用場與節點對的距離成反比，與節點對的數據傳輸能力成正比。為了模擬交通擁堵現象，為每一路段節點引入一個數據緩沖隊列，用于模擬當路段出現擁堵時車輛的排隊現象。根據以上分析，可以重新定義網絡中任意節點對之間的引力為

式（1）可以看作節點對之間的引力方程。其中，fij為任意節點i，j之間的引力；k為常數；ci，cj為節點i和j的傳輸能力，即單位時間內所能處理的最大數據包個數；qi為節點i當前緩存隊列中的數據包個數；qj為節點j當前緩存隊列中的數據包個數，當兩個緩存隊列同時為0時表示節點對之間路徑暢通，無擁堵現象發生；cicj／（qi＋qj）可以看作當前節點對之間的路徑的暢通程度，它的取值條件是兩個緩存隊列不能同時為零，也就是兩個路段之間存在擁堵現象。在引力場理論中，引力場中某一點所受引力與暗能量的虛擬質量和星體質量的乘積成正比，與該點到旋轉中心的距離的平方成反比，且與物體的質量無關。對于復雜網絡而言，節點等價于星體，而節點的傳輸能力等價于星體的質量，傳輸能力越大，則引力就越大，因此cicj／（qi＋qj）定義中，路段越擁堵路段節點之間的引力越小，反之引力越大；路段傳輸能力越大路段之間的引力越大；dij為節點i到節點j的最短路徑長度；a和γ為兩個可調節參數，分別用于調節數據傳輸對節點暢通程度、節點傳輸能力和路徑長度的依賴程度，且a＞0；γ＞0。

1.2.2 節點的引力場的計算

把復雜交通網絡G看作是一個包含n個節點及其相互作用的系統，每個節點周圍存在一個虛擬的作用場，網絡中的任何節點都將受到其他節點的聯合作用，由此在整個網絡拓撲上確定了一個數據場，稱之為拓撲勢場。真實網絡的模塊化與抱團特性表明：節點間的相互作用具有局域特性，每個節點的影響能力會隨網絡距離的增長而快速衰減。根據以上分析，引入m階鄰居節點的概念。節點的引力場不僅僅與一階鄰居節點相關還與周圍從2，…，m階的鄰居節點發生關系，因此定義某個節點的引力場為一階到m階鄰居節點與該節點的引力的和。我們引入了衰減指數函數μm作為引力計算每項取值的系數描述了引力大小隨著距離的增加而衰減的趨勢。路網中任意節點i的引力場計算公式為

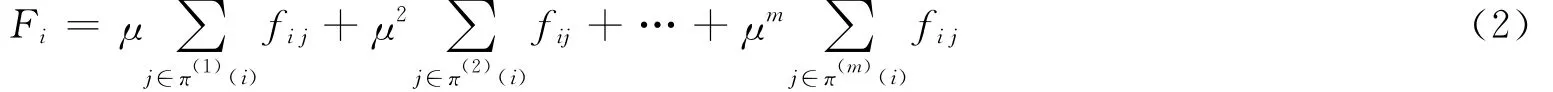
式中，Fi為節點i所激發的引力場取值，衰減指數μm，其中m取值為1，…，m，為各階引力場的系數，原則上與節點i越相近的節點對i產生的引力場越大，與i相距越遠的節點對i產生的引力越小，因此系數項取值0≤μ≤1。隨著距離階數的增加，系數項取值越小，這表明了距離階越大對節點i產生的引力越小。

1.3 路網節點重要度評估方法

網絡中的任何節點都將受到其他節點的聯合作用。因此，節點的重要度不僅與一階鄰居節點相關，還與網絡中所有的節點相關。定義路段重要度評估函數為

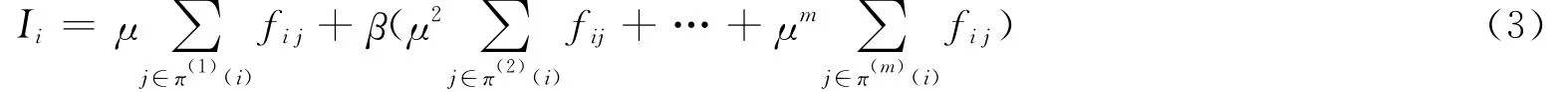
該評估函數中，當β＝0時，評估函數的評估結果只與一階節點相關，因此評估結果等價于基于度的評估結果；而β的取值滿足0＜β≤1時，該系數的取值直接代表了二階以上的節點對節點重要度的貢獻，我們將在實驗結果中討論β的取值對重要度的排序結果的影響。

已知GIS復雜路網，所考察鄰居節點深度為m，根據以上分析我們提出評估路段節點重要度的具體算法為：1）從GIS路網結構圖映射出對偶拓撲結構：G＝ ｛ V ， L｝。V是路網的頂點集合，也是路網的路段集合。L是路網的邊的集合，也是路網的交叉路口的集合。2）根據對偶拓撲結構，提取任意節點i的1到m階鄰居節點集：π（1）（i），π（2）（i），…，π（m）（i）；3）根據引力場路由算法為路網動態配流。4）計算節點i的各階鄰居節點集的每個階的引力和：確定節點i的引力場Fi； 5）根據式（3）計算每個節點的重要度，輸出Ii。

2 試驗與仿真

2.1 城市交通路網關鍵道路提取以及路網的配流

根據成都市城區2007年街道詳圖，按路名提取197個路段，構建原始廣義路網拓撲。基于該路網結構，采用對偶拓撲方法以道路為節點、交叉口為邊構建路網對偶圖。為了能夠較好地描述路網的整體結構和復雜性，將本文的路段重要性評估方法引入到路網關鍵道路提取中，修改文獻［13］算法為路網對偶圖提取10條關鍵道路如圖2所示。

傳統均衡配流是從全局流量分布的角度實行路段交通流的動態分配，缺乏對人們交通出行認知知識的考慮。從行為認知學角度，人們的空間行為由類似于萬有引力定律的規律所決定［21］，故人們的交通出行行為也應可以用引力模型來描述。所以，為得到更符合實際的交通模擬結果，本文的路網配流方法采用文獻［11］中的引力場路由方法，具體方法如下：假設在給定的復雜網絡上，每個節點都具有如下的功能：路由、接收數據包、發送數據包。網絡的初始負載為0，每一個時間步t會產生r個數據包。這些數據包在網絡中傳輸會隨機地選擇源節點與目標節點。產生的數據包自動地添加到源節點的數據包緩存隊列的尾部，在單位時間步內每個節點最多能發送ci個數據包，節點的緩存隊列長度無限且采用先進先出方式。在網絡傳輸過程中，數據包總是由當前節點發送給某個鄰居節點，若該鄰居節點為數據包的目標節點，則刪除該數據包；否則，按照引力場路由選擇策略進入該鄰居節點的緩存隊列。

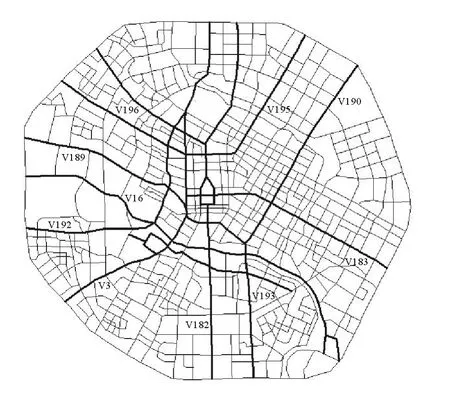
圖2 關鍵道路圖Fig.2 Key road map

2.2 試驗結果仿真分析

為了驗證本文算法的有效性，根據本文的計算方法，采用引力場路由的策略為路網進行配流，得到了路網的擁堵與非擁堵的臨界狀態負載的取值Rc＝12。在空閑狀態，路網非擁堵取R＝6，即R＜Rc；在最大臨界狀態，路網處于擁堵與非擁堵的臨界值，取R＝12，即R＝Rc；在擁堵狀態，取R＝20，即R＞Rc，3種狀態下的交通流數計算出了197個路段節點的引力場的取值，根據圖2提取的關鍵道路選擇：V182，V190，V192，V195，V183，V16，V3，V189，V196，V193這條關鍵道路作為仿真分析結果的評估。

表1為10條關鍵道路在路網處于空閑狀態、臨界狀態以及擁堵狀態下的引力情況。在空閑狀態下，各節點緩存隊列中數據包數為0，各個節點的引力場重要度排序結果與基于節點度的方法比較接近，其原因是公式（1）在節點緩存隊列為0時，度越大的節點其引力作用越大；而在臨界狀態與擁堵狀態下節點的重要度排序結果都與基于節點度的評價方法存在明顯差別。隨著負載量的增加，各節點緩存隊列中數據包數不再為0，且節點的擁堵程度與其緩存隊列中數據包數基本成正比關系。根據公式（1）可知，節點越擁堵，節點間的引力就越小，那么公式（2）所計算的節點引力場值也越小。根據表2可以看出：當R＝6時最重要路段為182號，隨著182號路段擁堵增加到臨界狀態，當R＝12時，16號路段是最重要的路段，而182號路段排序在最后，這說明182號路段的擁堵程度在10個節點中最嚴重。而當R＝20時候，路網陷入全面擁堵狀態，這時193號路段最重要，而182號路段依舊是最擁堵的路段。由此表明：1）擁堵可以改變路段在路網中的重要程度；2）在空閑狀態下，路段的重要性取決于路段的結構特性，即度、中心性等；3）在擁堵狀態下，從行為認知學角度，越擁堵的路段由于其已經匯聚了大量交通流，在路段擁堵沒有得到一定緩解的情況下，該路段對其他交通流的吸引力將下降，進而降低了該路段在路網中的重要程度。故本文的節點重要度研究方法能實時反映路段的擁堵狀況，出行者可以根據節點重要度的排序結果選擇出行的路徑。

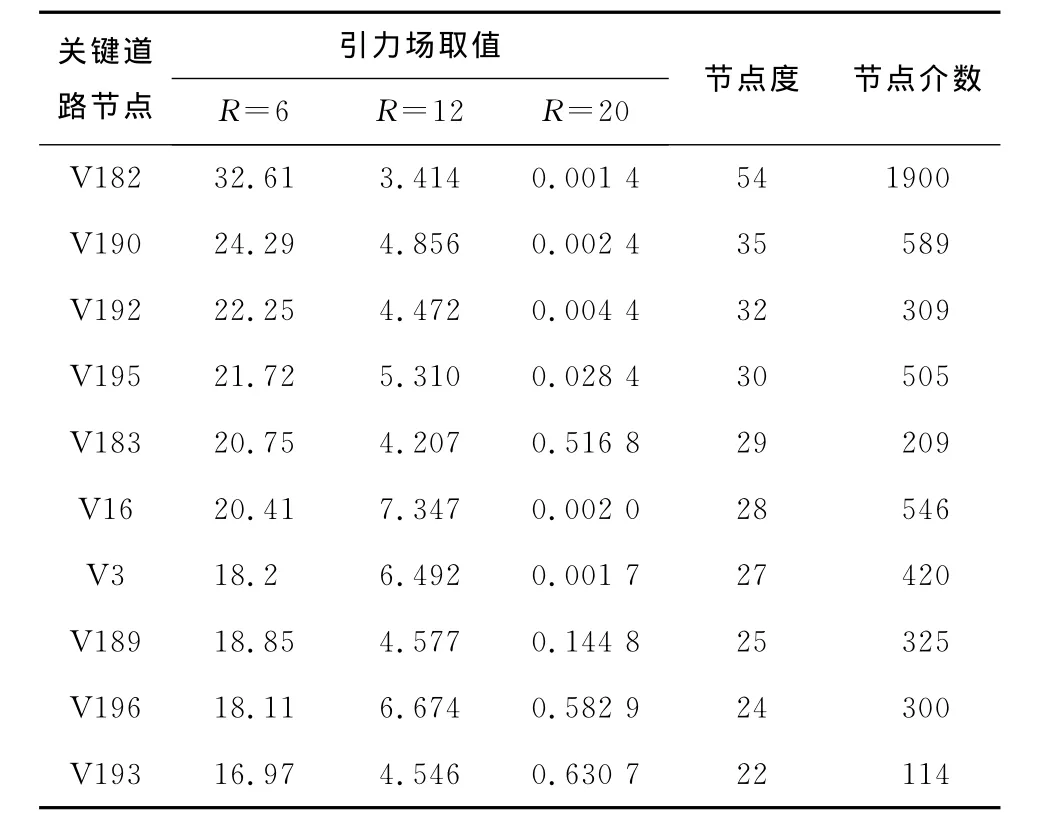
表1 路網關鍵道路節點引力場、度、介數Tab.1 Indices of gravitational field degree betweenness in road network’s key road node

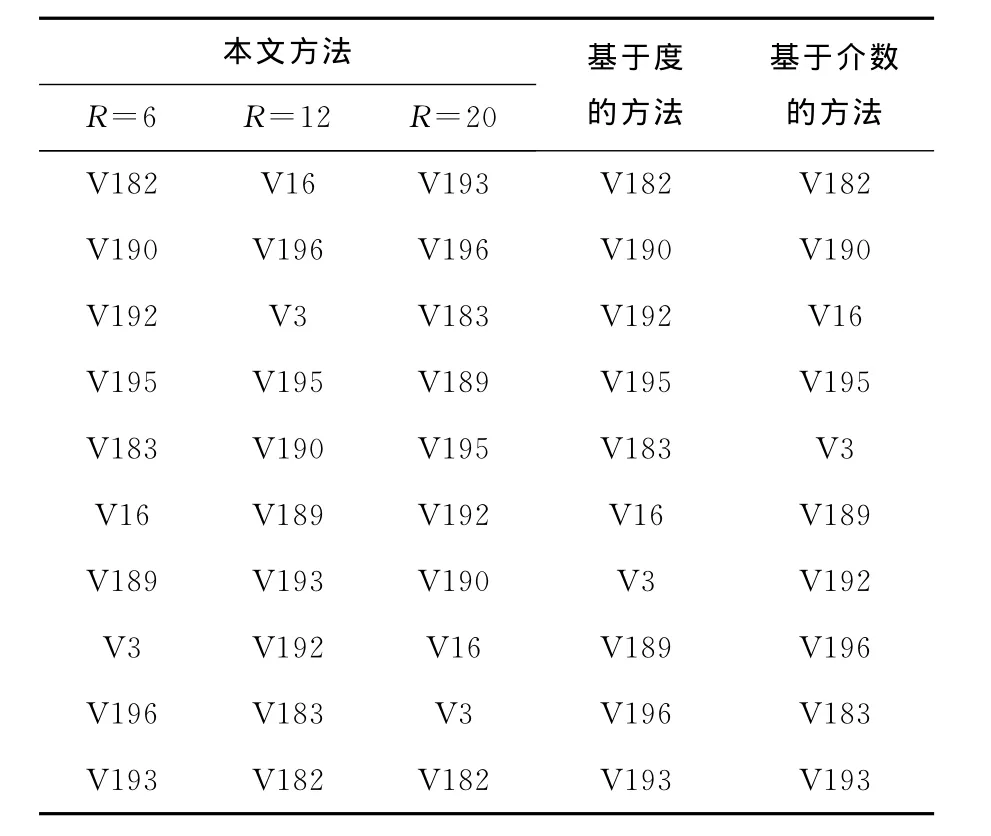
表2 路網關鍵道路節點重要度評價結果（降序）Tab.2 Node importance evaluation results in road network′s key road node

由圖3可以看出，節點重要度評估結果與m的取值密切相關。理論上，m的取值滿足 ［ 0，D ］區間。為進一步分析m為何值時本文評估方法可得到準確的評估結果，分別在路網的不同負載下研究了節點重要度隨m的變化情況。如圖3所示，a，b，c分別給出了路網中10個關鍵道路節點在R＝6無擁堵狀態、R＝12擁堵與非擁堵臨界狀態、R＝20完全擁堵狀態3種情況下重要度與m值的關系。由仿真結果可知，節點重要度評估結果隨m值的增大總體呈現“由不穩定到穩定”的變化趨勢，且當m小于網絡平均路徑長度L時（即m＜L），節點重要度I隨m的增加變化較大，為不穩定狀態；而當m大于網絡平均路徑長度L（即m＞L），節點重要度I隨m值的持續增加幾乎不再變化，節點的重要度評估結果進入穩定狀態（仿真中L的取值為5）。由此，可以得出一個重要結論：只要考察的鄰居節點深度m值大于網絡的平均路徑長度L，本文評估方法便能得到準確、可靠及高精度的評估結果。

圖3 節點重要度與m值的關系Fig.3 Relationship between value of mand node importance

由公式（2）和（3）可知，μ用于衡量節點引力場隨距離的衰減趨勢，故取值滿足0≤μ≤1；β用于評估二階以上節點對當前節點重要度的貢獻，從空間自相關可知，節點自身屬性對其重要性的貢獻程度應大于其他節點對該節點的影響，故β取值應滿足0≤β≤1。故可以通過調節μ，β的取值組合分析節點引力場對多階鄰居節點及自身特性的敏感程度。為進一步檢驗本文方法的有效性，對不同μ，β取值下路段的引力場情況及重要程度進行仿真。實驗數據表明：在非擁堵狀態和擁堵臨界狀態下μ，β的取值對節點重要度的排序沒有影響，而在擁堵狀態下μ，β的取值對重要度的排序有影響。表3是在擁堵狀態下μ，β的取值與關鍵路徑節點引力場的取值關系圖，仿真中令m＝3，R＝12。表4是表3的關鍵路徑節點重要度的排序結果。由引力場的定義可知，擁堵會使引力場的取值減小。隨著擁堵的增加路網中很多節點引力場的取值趨向于0或為0。表3的第一列數據恰好印證了這一定義。引力場取值為0的節點（路段182，190，192，16，3）用于重要度排序中不能得出正確的排序結果，在表4中μ＝0.2的時候，最后5個節點的重要度排序是不準確的，隨著μ的取值的增加表4中最后5個節點的重要度排序能得出精確的結果。而當β＝0.2時，表3的第2列數據有4個節點的引力場取值相同（190，192，16，3），在表4中這4個節點的重要度排序結果也是不正確的，隨著β值的增加，在表4的最后兩列能得到精確的節點重要度的排序結果。

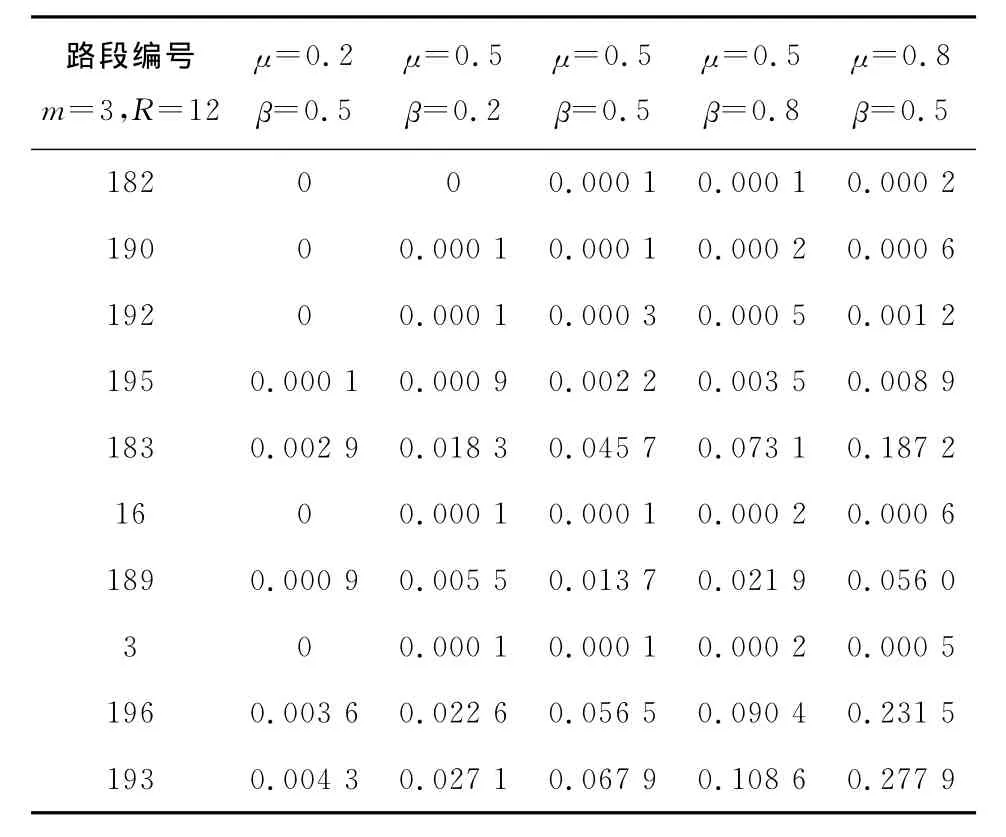
表3 擁堵狀態下μ，β取值與關鍵路徑節點引力場關系Tab.3 Relationship between the values ofμ，βand nodes in the key road of gravitational field in the state of congestion

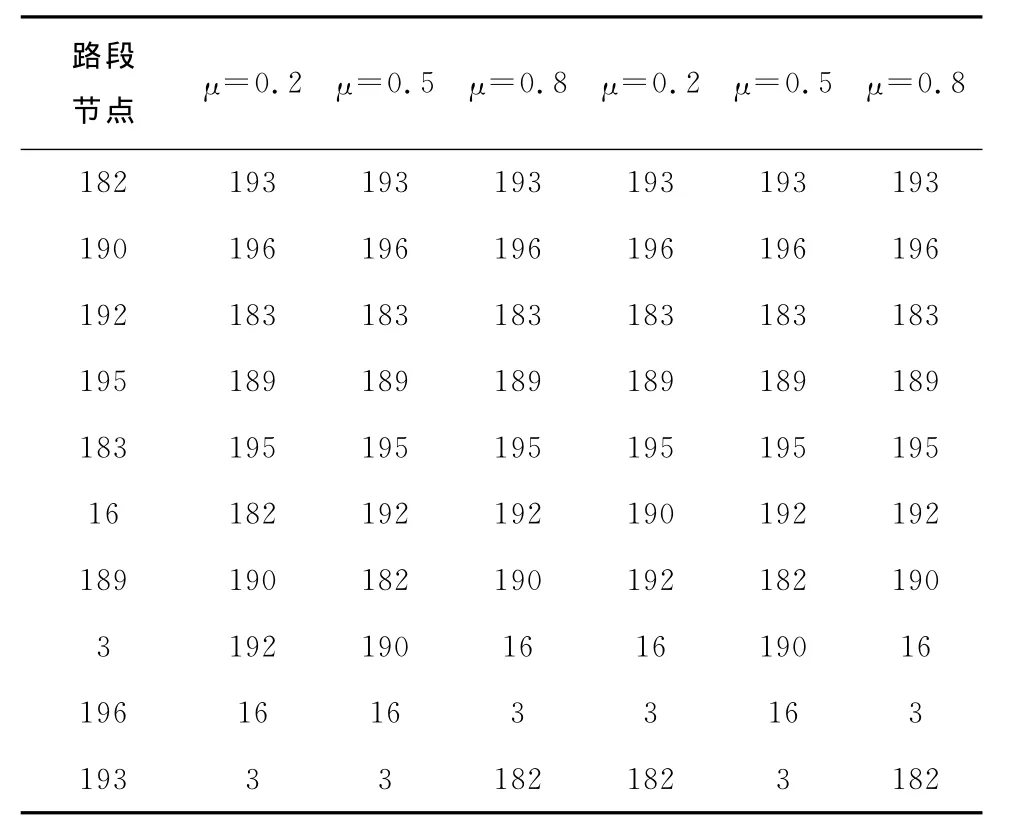
表4 擁堵狀態關鍵路徑節點重要度排序結果（降序）Tab.4 Key road node importance ranking results in the state of congestion

3 結論

對路網中道路重要性的動態、快速、準確的評價對交通計劃、控制和指揮服務有著重要的意義。目前道路重要性評估中的主要困難是難以采用動態的方法準確地接近實際地模擬路網的實際運行情況。本文研究的基于場論的城市道路重要性評估方法采用動態的路網配流技術，在路段引力場的定義中模擬了路段的擁堵排隊現象，使最后的路段評估模型能動態體現路段的擁堵狀況。實驗結果表明：本文的評估方法能進一步揭示復雜路網中的擁堵節點對重要性的影響。通過在評估模型中定義參數μ，β調節了路段節點引力場的取值，解決了評估函數在取相同值的時候無法得出正確的評估結果的問題。本文的評估模型能夠幫助人們理解路網上路段在擁堵下的重要性的依賴關系，為發現復雜路網的關鍵路徑節點提供了一種新的研究思路。

［1］ 李清泉，曾喆，楊必勝，等.城市道路網絡的中介中心性分析［J］.武漢大學學報（信息科學版），2010，35（1）：37－41.Li Qingquan，Zheng Zhe，Yang Bisheng，et al.Betweenness centrality analysis for urban road networks［J］.Geomatics and Information Science of Wuhan University，2010，35（1）：37－41.

［2］ 鄭年波，陸鋒，段瀅瀅.道路轉向延遲的動態對偶圖模型［J］.中國圖象圖形學報，2010，（6）：915－920.Zheng Nianbo，Lu Feng，DuanYingying.Dynamic dual graph mode for turn delays on road networks［J］.Journal of Image and Graphics，2010，（6）：915－920.

［3］ 劉剛，李永樹，楊駿，等.對偶圖節點重要度的道路網自動選取方法［J］.測繪學報，2014，43（1）：97－104.Liu Gang，Li Yongshu，Yang Jun，et al.Auto－selection method of road networks based on evaluation of node importance for dual graph［J］.Acta Geodaetica et Cartographica Sinica，2014，43（1）：97－104.

［4］Port A S，Crucitt I P，Latora V.The network analysis of ur ban streets：a dual approach［J］.Physica A，2006，369（2）：853－866.

［5］ 高自友，吳建軍，毛保華，等.交通運輸網絡復雜性及其相關問題的研究［J］.交通運輸系統工程與信息，2005，5（2）：79－83.Gao Ziyou，Wu Jianjun，Mao Baohua，et al.Study on the complexity of traffic networks and related problems［J］.Journal of Transportation Systems Engineering and Information Technology，2005，5（2）：79－83.

［6］ Michael A P T.Applying interactive color graphics in traffic planning［J］.Computers ＆ Graphics，2007，11（3）：241－248.

［7］ 王曉麗，溫冬梅，張利分.交通網絡重要路段確定方法研究［J］.山西科技，2007，（1）：91－95.Wang Xiaoli，Wen Dongmeng，Zhang Lifen.Study on the method of defining important sections of the traffic network［J］.Shanxi Science and Technology.2007，（1）：91－95.

［8］ 侯立文，蔣馥.城市道路網中路段相對重要性研究［J］.系統工程理論方法與應用，2004，13（5）：623－627.Hou Liwen，Jiang Fu.Study on the relative importance of links in urban roads network［J］.Systems Engneering Theory Methodology Applications，2004，13（5）：623－627.

［9］ 劉思峰，萬壽慶，陸志鵬，等.復雜交通網絡中救援點與事故點間的路段重要性評價模型研究［J］.中國管理科學，2009，17（1）：119－124.Liu Sifeng，Wan Shouqing，Lu Zhipeng，et al.The importance of highway section evaluation model in complex network between accident point and rescue point in the emergency situations［J］.Chinese Journal of Management Science，2009，17（1）：119－124.

［10］赫南，淦文燕，李德毅，等.一種基于數據場的網絡節點重要性度量方法［C］／／中國人工智能學會第12屆全國學術年會論文匯編.哈爾濱：哈爾濱工業大學出版社，2009：55－60.He Nan，Gan Wenyan，Li Deyi，et al.Evaluate nodes importance in the network based on data field theory［C］／／Chinese Artificial Intelligence Society of the Twelfth National Academic ConferenceProceedings.Harbin：Harbin Institute of Technology press，2009：55－60.

［11］劉剛，李永樹.基于引力場理論的復雜網絡路由選擇策略研究［J］.物理學報，2012，61（24）：248901.Liu Gang，Li Yongshu.Routing strategy for complex networks based on gravitation field theory［J］.Acta Phys Sin，2012，61（24）：248901.

［12］李玉蘭，李耀堂.城市道路網容量的對偶圖算法［J］.云南大學學報（自然科學版），2006，（4）：293－297.Li Yulan，Li Yaotang.Dual graph algorithm for the volume of the city road network［J］.Journal of Yunnan University，2006，（4）：293－297.

［13］徐英睿，陸鋒，張洪巖.基于對偶圖的城市交叉口延誤分析［J］.公路，2012，（9）：149－153.Xu Yingrui，Lu Feng，Zhang Hongyan.Based on the dual graph analysis of the urban intersection delay［J］.Highway，2012，（9）：149－153.

［14］閆文彩，張玉林，趙茂先，等.基于復雜網絡的城市路網可靠性分析［J］.山東科學，2011，（2）：65－70.Yan Wencai，Zhang Yulin，Zhao Maoxian，et al.Complex network based reliability analysis of urban road networks［J］.Shangdong Science，2011，（2）：65－70.

［15］James P E，Martin G J.地理學思想史［M］.李旭旦，譯.北京：商務印書館.1989：481－482.

［16］Restrepo J R，Ott E，Hunt B R.Characterizing the dynamical importance of network nodes and links［J］.Phys Rev Lett，2006，97（9）：094102.

［17］Barthelemy M.Betweenness centrality in large complex networks［J］.Eur Phys J B，2004，38（2）：163－168.

［18］Lohmann G，Margulies D S，Horstmann A，et al.Eigenvector centrality mapping for analyzing connectivity patterns in fMRI data of the human brain［J］.PloS ONE，2010，5（4）：e10232.

［19］Jin J，Xu K，Xiong N，et al.Multi－index evaluation algorithm based on principal component analysis for node importance in complex networks［J］.IET Networks，2012，1（3）：108－122.

［20］Zhang J，Xu X K，Li P，et al.Node importance for dynamical process on networks：a multiscale characterization［J］.Chaos，2011，21（1）：016107.

［21］田志文，周海濤.引力模型預測交通分布量的誤差分析［J］.公路交通科技，1994，11（2）：47－51.Tian Zhiwen，Zhou Haitao.The error analysis of traffic distribution by gravity model［J］.Joural of Highway and Transportation Research and Development，1994，11（2）：47－51.