具有失真認知信息的兩層沖突環境建模與分析
宋業新,袁昊劼,李 凌
(海軍工程大學理學院,武漢430033)
0 引言
由于實際沖突系統的復雜多元化與多層次性,社會生活中的個體或組織常常處于具有兩個或多個層次的沖突或競爭環境中。深入研究這樣一類復雜沖突環境、探討其建模分析方法具有重要意義。
針對具有兩個層次的沖突問題,哈佛大學教授Putnam R D[1]首先提出了兩層對策框架,將外交與國內政治之間的聯系問題描述成一個兩層對策模型,并使用國際談判對策和國內政治對策兩個對策來討論國內和國際政治的糾紛。Ahmer T[2]運用兩層對策研究了具有雙邊國內約束的國際協商問題。Viguier L等[3]通過建立一個兩層對策結構模型,計算其唯一的均衡解來評價根據京都協議,歐盟貿易市場范圍內溫室氣體排放量的分配策略問題。Nanduri V等[4]應用兩層矩陣對策模型討論了能源市場中的發電容量擴充問題。然而,這些研究大都建立在局中人對沖突或協商環境有較為清晰的認識的基礎上,忽視了在實際沖突過程中,不同層次的局中人可能會對其他局中人的沖突信息具有不確定性認知或錯誤判斷。對此,Gorelik V A等[5-6]分別研究了帶有局中人策略估計和完全風險或風險函數等不確定性條件的遞階對策問題。Oyota T等[7]基于由3個雙矩陣對策構建的遞階超對策探討了兩國之間具有不確定性認知的國際國內兩層協商問題。本文則針對具有失真認知的兩層沖突環境,基于局中人之間策略集與結局偏好上的認知信息,將單方上、下層局中人與對方局中人之間的沖突分別描述為一個超對策[8-9]和多個雙矩陣對策,構建了具有失真認知信息的面向兩層沖突環境的兩層遞階超對策模型,并討論了其均衡結局的定義以及均衡結局存在的條件與求解方法。
1 具有失真認知信息的兩層沖突環境
考慮如下兩層沖突環境,A和B是沖突雙方,a和a1,a2,…,am分別是A方處于上層(例如,國際層面)和下層(例如,國內層面)的局中人,b是B方的局中人(由于具有代表性,不妨假設為其上層局中人)。記N1={a,a1,a2,…,am},N2={b},則N=N1∪N2為沖突環境中局中人的集合,若Si(i∈N)為局中人i的策略集,Sji(i∈Np,j∈Nq;p,q∈{1,2},p≠q)為局中人i所認知的對方局中人j的策略集,由于認知失真或錯誤判斷,一般有Sji≠Sj,且fji:Sj→Sji為局中人i對對方局中人j真實策略集的認知函數,ki:Sai→Sa為A 方上層局中人a對其下層局中人ai(i=1,2,…,m)真實策略集的認知函數。另外,在局中人i與j的沖突中,Vi為局中人i在其所認知的結局空間Oi=Si×Sji上的偏好值向量,Vi(o(k)i)表示其對結局o(k)i∈Oi的偏好值;Vji為局中人i所認知的局中人j在結局空間Oi上的偏好值向量,同樣,由于認知失真或錯誤判斷,一般有Vji≠Vj。針對上述具有失真認知信息的兩層沖突環境,本文將討論其建模與分析方法。
2 兩層遞階超對策模型及其遞階超納什均衡
2.1 兩層遞階超對策模型
本文從描述A方上、下兩層局中人與對方局中人之間沖突的角度來建立兩層遞階超對策模型。
首先,A方上層局中人a與B方局中人b對沖突環境存在不同的認知信息,他們分別根據自己的認知構建對策模型Ga= (Sa,Sba;Va,Vba)和Gb= (Sab,Sb;Vab,Vb)。由Ga和Gb構成局中人a與b之間的兩人一階(或簡單)超對策模型,記為H0= [Ga,Gb]。結合a與b之間相互真實策略集上的認知函數fba:Sb→Sba和fab:Sa→Sab,可進一步建立局中人a與b之間的兩人共生超對策模型[7],表示為
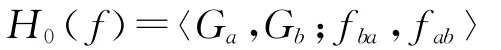
這里,
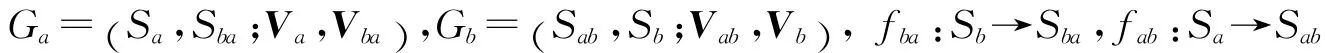
其次,在整個沖突中,A方下層局中人ai(i=1,2,…,m)為了應對b與己方上層局中人a的沖突,根據自身對局中人的b認知,單方主觀地構建與b的雙矩陣對策模型:
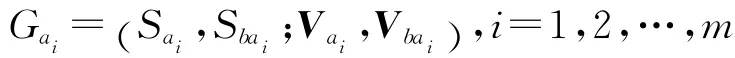
這樣,在上述共生超對策模型和雙矩陣對策模型的基礎上,結合A方下層局中人ai對B方局中人b真實策略集的認知函數fbai:Sb→Sbai,以及A方上層局中人a對下層局中人ai真實策略集的認知函數ki:Sai→Sa,構建A方所有局中人a,a1,a2,…,am與B方局中人b之間的兩層遞階超對策模型:
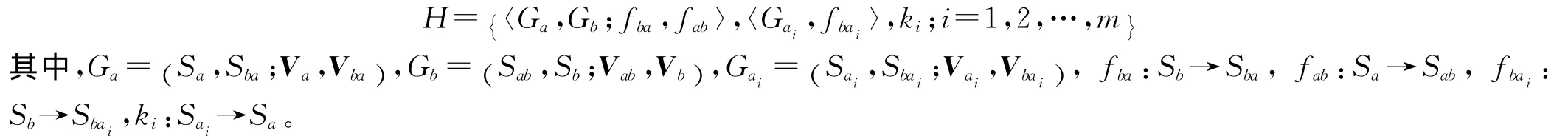
特別地,若A方所有局中人正確地認知b的策略集,而b也正確地認知a的策略集,即Sb=Sba=Sbai,Sa=Sab時,記fba=fbai=ISb,fab=ISa,局中人a,a1,a2,…,am與b之間的兩層遞階超對策稱為強兩層遞階超對策,表示為
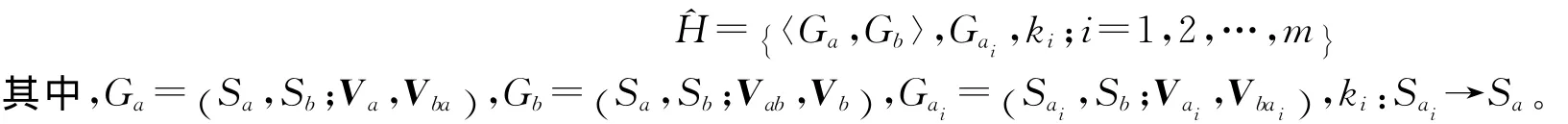
由于在國際貿易、協商談判、條約簽署等活動中,雙方局中人往往會正確認知對方的策略集,因此,強兩層遞階超對策模型是具有實際意義的。
進一步,若雙方局中人不僅正確認知對方的策略集,而且清晰準確地了解對方的結局偏好,即Va=Vab,Vb=Vba,Vbai=Vbi,這里Vbi是局中人b在結局空間Sai×Sb上的結局偏好向量,此時,局中人a,a1,a2,…,am與b之間的強兩層遞階超對策就轉化為清晰的兩層對策,可以表示為
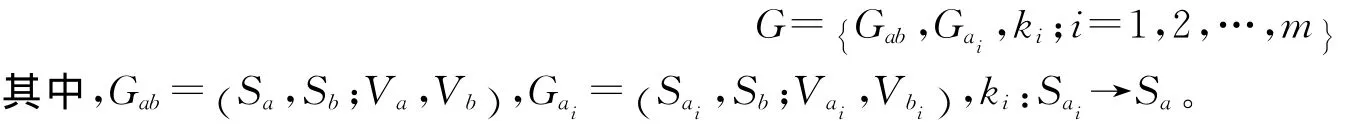
2.2 遞階超納什均衡
為了給出兩層遞階超對策模型H遞階超納什均衡的定義,先介紹兩人簡單超對策和共生超對策超納什均衡的概念。
定義1[9]在兩人簡單超對策H0=〈Ga,Gb〉中,若是Gb的一個均衡結局,則是兩人簡單超對策H0的超納什均衡。若同時是Ga與Gb的均衡結局,則稱為H0穩定(可維持)的超納什均衡,否則,稱失穩的超納什均衡。
定義2[7]在兩人共生超對策模型 H0(f)=〈Ga,Gb;fba,fab〉中,若(x*,y*)∈Sa×Sb,且對于?x∈Sa,Va(x*,fba(y*))≥Va(x,fba(y*)),對于?y∈Sb,Vb(fab(x*),y*)≥Vb(fab(x*),y)。則稱(x*,y*)為兩人共生超對策模型H0(f)的超納什均衡。
由定義2,若(x*,fba(y*))是Ga的一個均衡結局,(fab(x*),y*)是Gb的一個均衡結局,則(x*,y*)為 H0(f)的一個超納什均衡。共生超對策的超納什均衡實際上是局中人a和b分別通過認知函數fba和fab所理解的納什均衡。
在上述兩個定義的基礎上,給出兩層遞階超對策模型H遞階超納什均衡的定義。
定義3 在兩層遞階超對策 H= {〈Ga,Gb;fba,fab〉,〈Gai,fbai〉,ki;i=1,2,…,m}中,結局若(α*,β*)是兩人共生超對策〈Ga,Gb;fba,fab〉的一個超納什均衡,對?i∈且在對策Gai中,對于?γi∈Sai有Vai(γi*,fbai(β*))≥Vai(γi,fbai(β*))。則稱(α*,是H的一個遞階超納什均衡。
由定義3可以看出,兩層遞階超對策的遞階超納什均衡實際上是根據認知函數fbai與ki(i=1,2,…,m)在兩人共生超對策的超納什均衡(α*,β*)基礎上的一種自然擴展。
定義4 對于?sb∈Sb,?si,s′i∈Sai,若Vai(si,fbai(sb))≥Vai(s′i,fbai(sb)),有Va(ki(si),fba(sb))≥Va(ki(s′i),fba(sb)),則稱認知函數集{fba,fbai,ki}滿足遞階一致性。
若fba=fbai=ISb,fab=ISa,則定義4變為:對于?sb∈Sb,?si,s′i∈Sai,若Vai(si,sb)≥Vai(s′i,sb),有Va(ki(si),sb)≥Va(ki(s′i),sb),則此時只稱認知函數ki滿足遞階一致性。
定理1 若 H= {〈Ga,Gb;fba,fab〉,〈Gai,fbai〉,ki;i=1,2,…,m }是一個兩層遞階超對策,其中上層兩人共生超對策〈Ga,Gb;fba,fab〉存在超納什均衡(α*,β*),認知函數集{fba,fbai,ki,i=1,2,…,m}滿足遞階一致性,且ki,i=1,2,…,m,均為滿射,則兩層遞階超對策H存在遞階超納什均衡。
證明:由于(α*,β*)∈Sa×Sb是兩人共生超對策模型〈Ga,Gb;fba,fab〉的一個超納什均衡,故對?α∈Sa,有Va(α*,fba(β*))≥Va(α,fba(β*));?β∈Sb,有Vb(fab(α*),β*)≥Vb(fab(α*),β)。
又在對策Gai(i=1,2,…,m)中,針對fbai(β*)∈Sbai,一定?γi*∈Sai,對于?γi∈Sai有Vai(γi*,fbai(β*))≥Vai(γi,fbai(β*)),由認知函數集{fba,fbai,ki,i=1,2,…,m}的遞階一致性,有Va(ki(γi*),fba(β*))≥Va(ki(γi),fba(β*)),由于ki為滿射,ki(γi)可以是Sa中的任意策略,故ki(γi*)=α*,i=1,2,…,m。于是,由定義3,(α*,是H的一個遞階超納什均衡。證畢。
在強兩層遞階超對策模型中,由于fba=fbai=ISb,fab=ISa,類似于定理1,易得:
定理2 若H= {〈Ga,Gb〉,Gai,ki;i=1,2,…,m }是一個強兩層遞階超對策,其中上層兩人簡單超對策〈Ga,Gb〉存在超納什均衡(α*,β*),認知函數ki,i=1,2,…,m均滿足遞階一致性,且為滿射,則強兩層遞階超對策存在遞階超納什均衡。
由定理1,2和定義3,不難得出,如果遞階超納什均衡存在,只要先通過超對策穩定性分析過程[9-10]求出上層共生(或簡單)超對策的超納什均衡(α*,β*),然后,在對策Gai(i=1,2,…,m)中,根據定義3的條件(2)確定出γi*,即可得到兩層遞階超對策的遞階超納什均衡。
3 例子
A,B兩國為某爭議島嶼發生沖突,兩國高層分別記為局中人a和b,b的策略集Sb={β1,β2}={派兵駐守島嶼,撤出島嶼},a的策略集Sa={α1,α2,α3}={武力進攻,經濟制裁,外交談判}。面對沖突,A國的國防部和商務部(分別記為局中人a1,a2)會相應采取措施,a1的策略集Sa1={γ1,γ2,γ3,γ4}={空中進攻,海上進攻,封鎖,不派兵};a2的策略集Sa2={δ1,δ2,δ3}={為部隊提供后勤保障支援,限制B國商品進出口,不采取行動}。假定A方所有局中人正確地認知b的策略集,而b也正確認知a的策略集,但相互的結局偏好認知失真,a對局中人a1,a2真實策略集的認知函數均為滿射,且有k1(γ1)=α1,k1(γ2)=α1,k1(γ3)=α2,k1(γ4)=α3;k2(δ1)=α1,k2(δ2)=α2,k2(δ3)=α3。
若上層局中人a和b之間的簡單超對策信息見表1,表中每個括號中的4個數據分別表示針對結局空間Sa×Sb上的結局(αi,βj),a和b 的真實偏好值Va(αi,βj),Vb(αi,βj),以及a所認知的b的偏好值Vba(αi,βj)與b所認知的a的偏好值Vab(αi,βj)。這里為簡便起見,用1~6的整數來反映對6個不同結局的偏好值。
A方局中人a1,a2分別根據主觀認知,構建與B方局中人b的對策模型,其結局和偏好信息分別見表2和表3,表2中每個括號中的2個數據分別表示針對結局空間Sa1×Sb上的結局(γi,βj),a1的偏好值Va1(γi,βj)和a1所認知的b的偏好值Vba1(γi,βj),用1~8的整數來表示;表3中每個括號中的2個數據則分別表示針對結局空間Sa2×Sb上的結局(δi,βj),a2的偏好值Va2(δi,βj)和a2所認知的b的偏好值Vba2(δi,βj),用1~6的整數來表示。

表1 a和b之間的簡單超對策〈Ga,Gb〉Tab.1 Simple hypergame〈Ga,Gb〉between aand b
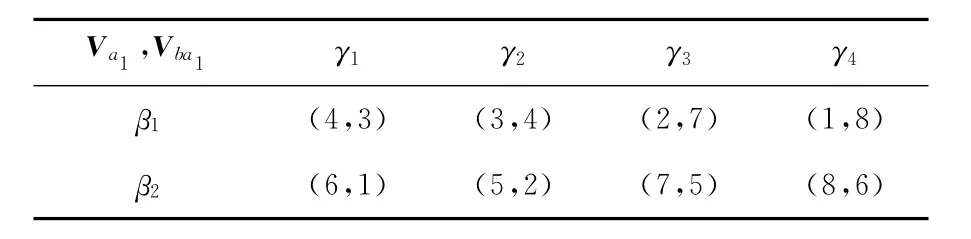
表2 a1和b之間的雙矩陣對策Ga1Tab.2 Bimatrix game Ga1between a1and b

表3 a2和b之間的雙矩陣對策Ga2Tab.3 Bimatrix game Ga2between a2and b
4 結論
針對具有失真認知的兩層沖突環境,基于局中人之間策略集與結局偏好上的認知信息,以及位于不同層次的局中人與對方局中人之間的對策和超對策,構建兩層遞階超對策模型。在超對策超納什均衡的基礎上,給出了兩層遞階超對策模型遞階超納什均衡的定義,探討了遞階超納什均衡存在的條件及其求解方法。論文給出的模型和方法對于復雜多層沖突環境的建模與分析具有指導意義。
[1] Putnam R D.Diplomacy and domestic politics:the logic of two-level games[J].International Organization,1988,42(3):427-460.
[2] Ahmer T.International bargaining with two-sided domestic constraints[J].Journal of Conflict Resolution,2001,45:320-340.
[3] Viguier L,Vielle M,Haurie A,et al.A two-level computable equilibrium model to assess the strategic allocation of emission allowances within the European union[J].Computers and Operations Research,2006,33:369-385.
[4] Nanduri V,Das T K,Rocha P.Generation capacity expansion in energy markets using a two-level game-theoretic model[J].IEEE Transactions on Power Systems,2009,24(3):1165-1172.
[5] Rodyukov A B,Tarakanov A F.On the solution of hierarchical game under uncertainty with total risk of players[J].International Journal of Computer and Systems Sciences,2007,46(5):681-687.
[6] Gorelik V A,Rodyukov A V and Tarakanov A F.A hierarchical game under uncertainty conditions with using player risk function and guarantied strategy estimate[J].International Journal of Computer and Systems Sciences`,2009,48(6):937-945.
[7] Toyota T and Kijima K.Modelling of two-level negotiation in hierarchical hypergame framework[C]//Proc of 2004AI,Simulation and Planning Conference.Berlin Heidelberg:Springer-Verlag,2004:298-295.
[8] Gharesifard B,Cortes J.Evolution of players'misperceptions in hypergames under perfect observations[J].IEEE Transactions on Automatic Control,2012,57(7):1627-1640.
[9] 宋業新,王法坤,瞿勇.多沖突環境下的兩人一階超對策交互集結模型[J].系統工程與電子技術,2010,32(8):1672-1676.Song Yexin,Wang Fakun,Qu Yong.Interactive integration model of two-person first-level hypergames in multi-conflict situations[J].Systems Engineering and Electronics,2010,32(8):1672-1676.
[10]Song Y X,Li W J,Zeng X H.λ-Equilibrium of hypergame with fuzzy strategy and preference perceptions[C]//Proc of the IEEE International Conference on Intelligent Computing and Intelligent Systems.Washington:IEEE Press,2009,2:641-645.

