解析幾何課程創(chuàng)新學習方法的探索與實踐

張 微 孫梅蘭 章玉澤 趙春影 嚴建國 王學為

（合肥學院數(shù)學與物理系，安徽 合肥 230601）

我們在講授和學習解析幾何課程的過程中深刻體會到傳統(tǒng)的“只注重本課程理論體系的完整性”的方法，很難適應(yīng)現(xiàn)在的人才培養(yǎng)要求。因此，我們對解析幾何課程的學習模式從以下幾個方面進行了探討。希望能幫助學生學會學習該課程，增加學習興趣，減少學習困難，讓學生更快地、無障礙地進入后繼課程的學習，熟練地將所學的解析幾何知識應(yīng)用于實際。

1 優(yōu)化學習素材，提高學習效能

首先，我們根據(jù)學習和實習的經(jīng)驗，匯總了解析幾何知識在后繼課程和實際中應(yīng)用較多的“點”，對這些知識點進行“強化”處理。將這些知識點在教材的有關(guān)章節(jié)中標注，一方面提醒教師在教學中力爭對這些“點”講多、講深、講透，并介紹它們在后繼課程或?qū)嶋H中的作用；另一方面提醒學生在學習時重點關(guān)注。這樣，不僅讓學生對當下所學知識有更深的理解，而且讓學生對未來要學的知識有初步的感知并產(chǎn)生好奇心，從而提高學生的學習熱情。

例如，向量的外積在物理學中表示力矩、磁力、角動量等；參數(shù)方程是學生不夠重視且比較怕學習的部分，但參數(shù)方程在數(shù)學分析等學科中有非常廣泛的應(yīng)用，如用于求解各類積分，參數(shù)方程還廣泛地應(yīng)用于生產(chǎn)實際中；學生以往常常忽視對空間區(qū)域的作圖，認為可有可無，但會作圖對求解重積分、曲面積分等是非常有用的。

再如，目前學習的二維、三維向量在代數(shù)中會推廣到n 維；現(xiàn)在學習的平面間的位置關(guān)系可以用代數(shù)中線性方程組的解的結(jié)構(gòu)理論來討論、二次曲面的分類問題可以用代數(shù)中的二次型的理論來研究。

其次，對解析幾何教材中在后繼課程和實際中應(yīng)用較少的知識點進行適當?shù)摹叭趸碧幚怼１热纾蛄康碾p重向量積等。

另外，我們還遴選了幾本含有“應(yīng)用型”實例的參考書，汲取不同教材中的精華，歸納它們的特點，為更好地學習該門課程開闊視野，總結(jié)如何利用這些參考書配合主教材進行自主學習的經(jīng)驗。

2 提煉解析幾何課程中所蘊含的數(shù)學思想方法

有位哲學家指出：“即使是學生把教給他的所有知識都忘記了，但還能使他獲得受用終生的東西的那種教育才是最高最好的教育。”數(shù)學思想方法就是數(shù)學教育中使學生受用終生的東西之一。我們根據(jù)在解析幾何教與學中的經(jīng)驗，挖掘出解析幾何課程中所蘊含的數(shù)學思想方法，這些思想方法可以使解析幾何的教與學的高度得到極大的升華。解析幾何中蘊涵著數(shù)形結(jié)合、化歸、變換、類比、知識系統(tǒng)化等非常多的數(shù)學思想方法，這里僅以數(shù)形結(jié)合思想方法說明如下：

解析幾何是體現(xiàn)數(shù)形結(jié)合思想方法的典范，其內(nèi)容從始至終都貫穿著數(shù)形結(jié)合思想方法。教材的知識脈絡(luò)基本如下：介紹了向量及其運算，把空間的幾何結(jié)構(gòu)向量化、代數(shù)化，從而把代數(shù)的方法引入到幾何中來。又引入了坐標系，建立了空間向量的坐標與空間點的坐標，給出了向量各種運算的坐標表示，從而使向量的運算轉(zhuǎn)化為數(shù)的運算，這樣就把幾何問題的討論推進到了可以計算的數(shù)量層面；建立曲線、曲面與其方程的對應(yīng)關(guān)系；在由平面和直線滿足的幾何條件建立起它們的方程后，用代數(shù)的方法研究點、線、面間的幾何問題（位置問題、度量問題）；由柱面、錐面、旋轉(zhuǎn)曲面的幾何特征推導(dǎo)出它們的方程；通過對橢球面、雙曲面與拋物面的標準方程的討論得出它們的形狀和一些幾何性質(zhì)；從二次曲線（面）的方程出發(fā)，通過代數(shù)運算，找出適當?shù)淖鴺俗儞Q，得出二次曲線（面）的標準方程，從而能在平面上（空間中）確定它的位置，畫出它的幾何圖形。[1]

下面，舉例說明數(shù)形結(jié)合思想方法如何用于提高解題效率。

例1 已知兩條異面直線l1，l2，證明：連接l1上任一點和l2上任一點的線段的中點在兩直線的公垂線段的垂直平分面上。

解題思路：先建立空間直角坐標系，再寫出l1,l2在此直角坐標系下的方程，最后證明l1上任一點與l2上任一點中點的坐標滿足兩直線的公垂線段的垂直平方面的方程。

上題是用代數(shù)方法解決幾何問題。

例2 已知：x2+y2+z2=1，a2+b2+c2=1，求證：ax+by+cz≤1。

解題思路：由x2+y2+z2=1 知點(x,y,z)在以原點為球心的單位球面上；平面ax+by+cz=0 過原點；點(x,y,z)到平面ax+by+cz=0 的距離是此距離應(yīng)該小于等于單位球面的半徑，得出結(jié)論。

上例是用幾何方法解決代數(shù)問題。

3 總結(jié)利用案例學習的經(jīng)驗

我們?yōu)榻馕鰩缀蔚拿總€知識模塊尋找了至少一個實際應(yīng)用案例，分析如何利用這些案例來理解相關(guān)知識，如何建模并解決這些案例中的問題。通過所學知識的應(yīng)用，擴展知識面，提高學習興趣，增強分析與解決問題的能力。

例3[2]激光測量中的直線與平面問題

由激光知識可知，若圖1 中光軸為z 軸，則由點P 的激光在平面π 上點Pi(xi,yi,zi)(i=1，…，n)的光強為：

式中的z0為點P 的豎坐標。

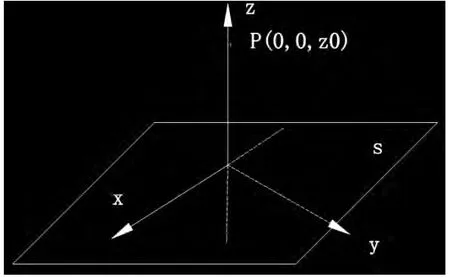
圖1

由于平面π 過坐標原點，所以其方程可記為

圖2

下面要求出A,B,z0，為此我們要在平面π 上確定若干點Pi(xi，yi，zi)(i=1，…，n)，為方便計算，構(gòu)造如圖2 中結(jié)構(gòu)的邊長為r 的組合等邊三角形，將這些三角形的頂點作為Pi(xi，yi，zi)(i=1，…，n)點，要求出Pi(xi，yi，zi)(i=1，…，n)的坐標和A,B,z0共3n+3 個未知量，需要3n+3 個方程。由Pi(xi，yi，zi)(i=1，…，n)的坐標滿足方程（1）和（3）式，會產(chǎn)生2n 個方程，還需要3n+3-2n=n+3 個方程。

圖2 的結(jié)構(gòu)中任意相鄰兩點間的距離均是邊長r，此結(jié)構(gòu)中共有(n-1)+(n-2)=2n-3(n≥2)條鄰邊，由此可得2n-3 個方程，所以令2n-3=n+3 有n=6。

因此，通過求解如下方程組：

求解上面的21 個方程得A，B，z0和Pi(xi，yi，zi)(i=1，…，n)的坐標。

上例可以作為“直線與平面”這部分知識的應(yīng)用案例。

例4[3]飛機機翼的外形曲面

某型號飛機的機翼為直紋面，圖3 表示兩個平行截面之間的機翼外形。橫截面的邊界是兩條參數(shù)閉曲線：

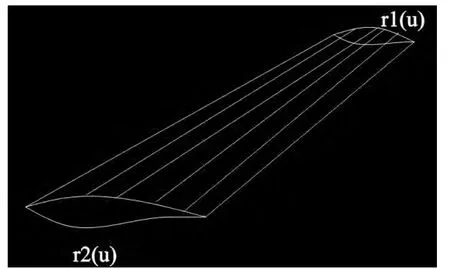
圖3

對于同一參數(shù)u1，在兩截面的邊界線分別對應(yīng)兩點這兩點之間的直線向量式方程為

其中(0≤v≤1)為參數(shù)。當u1從0→1 時，上直線就連續(xù)地描出一張直紋曲面，此直紋曲面的方程可以寫為：

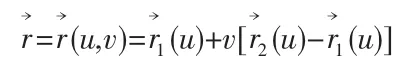
其中0≤u，v≤1 為曲面的參數(shù)。

上例作為學習“直紋曲面”這部分知識的應(yīng)用案例。

4 總結(jié)如何利用信息技術(shù)學習解析幾何的經(jīng)驗

我們探討設(shè)計了一些該課程的數(shù)學實驗項目。如運用Mathematica、Matlab 等軟件制作“解析幾何”中的曲面和曲線圖形，通過動態(tài)演示形象地揭示幾何概念的內(nèi)涵，清晰地展現(xiàn)幾何圖形的構(gòu)造和特點，增強學習的直觀性和形象性，多角度、多側(cè)面、多層次深化學習內(nèi)容，從而增加課程的趣味性，激發(fā)同學學習的積極性，加深對知識的理解，取得傳統(tǒng)式學習難以達到的效果。

例5[4]利用Matlab 畫出的圖像。

輸入如下命令：[x，y]=meshgrid(-4：0.5：4);z=sqrt(x.^2+y.^2);surf(x，y，z)

運行結(jié)果為所求圓錐面的圖像（略）。

本文是我們在實施安徽省大學生創(chuàng)新訓(xùn)練項目“解析幾何模塊化進程中創(chuàng)新學習方法的探索與實踐”的過程中的收獲和感悟。該項目的特色是首先考慮到解析幾何課程的特點，再從學生自身學習的角度出發(fā)，希望在總結(jié)解析幾何知識在后繼課程和實際應(yīng)用的基礎(chǔ)上，探索出解析幾何課程的創(chuàng)新學習方法并付諸實踐。

［1］呂林根.解析幾何學習輔導(dǎo)書[M].北京：高等教育出版社，2006.

［2］徐陽，楊興云.空間解析幾何及其應(yīng)用[M].哈爾濱：哈爾濱工業(yè)大學出版社，2006.

［3］蔣大為.空間解析幾何及其應(yīng)用[M].北京：科學出版社，2004.

［4］汪曉銀，鄒庭榮，周保平.數(shù)學軟件與數(shù)學實驗[M].2 版.北京：科學出版社，2010.

［5］馬淑云，王陽.解析幾何教學中強化數(shù)學思想方法芻議[J].南陽師范學院學報，2011，10(3)：87-91.

［6］王穎.將解析幾何融入線性代數(shù)教學中的思考[J].高師理科學刊，2013，33(4)：62-64.