用平面幾何證明三角形重心的性質(zhì)

王欣

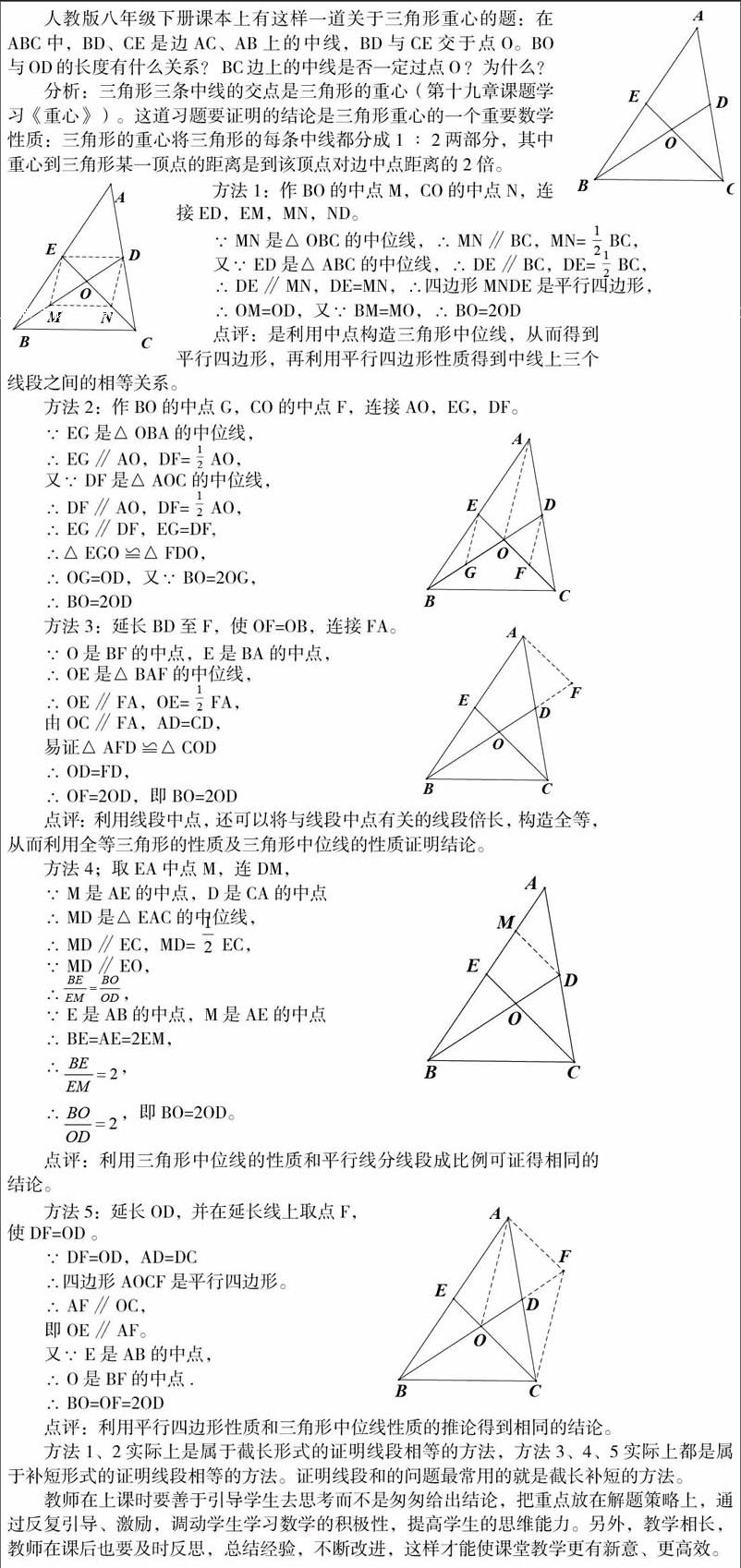
人教版八年級下冊課本上有這樣一道關(guān)于三角形重心的題：在ABC中，BD、CE是邊AC、AB上的中線，BD與CE交于點O。BO與OD的長度有什么關(guān)系？BC邊上的中線是否一定過點O？為什么？

分析：三角形三條中線的交點是三角形的重心（第十九章課題學(xué)習(xí)《重心》）。這道習(xí)題要證明的結(jié)論是三角形重心的一個重要數(shù)學(xué)性質(zhì)：三角形的重心將三角形的每條中線都分成1∶2兩部分，其中重心到三角形某一頂點的距離是到該頂點對邊中點距離的2倍。

點評：利用平行四邊形性質(zhì)和三角形中位線性質(zhì)的推論得到相同的結(jié)論。

方法1、2實際上是屬于截長形式的證明線段相等的方法，方法3、4、5實際上都是屬于補短形式的證明線段相等的方法。證明線段和的問題最常用的就是截長補短的方法。

教師在上課時要善于引導(dǎo)學(xué)生去思考而不是匆匆給出結(jié)論，把重點放在解題策略上，通過反復(fù)引導(dǎo)、激勵，調(diào)動學(xué)生學(xué)習(xí)數(shù)學(xué)的積極性，提高學(xué)生的思維能力。另外，教學(xué)相長，教師在課后也要及時反思，總結(jié)經(jīng)驗，不斷改進(jìn)，這樣才能使課堂教學(xué)更有新意、更高效。