輕松玩“轉”勾股定理
沈曉霞

轉化是將未知的問題轉化為已知的問題,把抽象的問題轉化為具體的問題,把復雜的問題轉化成簡單的問題.勾股定理研究的是平面直角三角形中三邊之間的關系,但在學習過程中時常會遇到立體圖形上的問題,這時就要考慮到運用轉化的思想,把立體圖展開成平面圖形,再利用平面幾何的知識進行求解.

例1 ? 如圖1所示,有一根高為2 m的木柱,它的底面周長為0.3 m,為了營造喜慶的氣氛,老師要求小明將一根彩帶從柱底向柱頂均勻地纏繞7圈,一直纏到起點的正上方為止,問小明至少需要準備多長的一根彩帶?
【分析】將一張直角三角形的紙片在鉛筆上纏繞七圈,將紙片展開,發現彩帶的長相當于直角三角形的斜邊長(如圖2),可以利用勾股定理求出彩帶的長.

解:∵BC為木柱的高,
∴BC=2 m.
又∵木柱的底面周長為0.3 m,
∴AC的長為0.3×7=2.1(m).
在Rt△ACB中,由勾股定理,得AB2=AC2+BC2=22+2.12=8.41,=2.9.
因此彩帶的長為AB=2.9 m.
【點評】遇到一些空間問題時,可通過動手實際操作一下,建立實物模型,這是建立空間概念的良好訓練方法,而對實際問題進行分解、轉化是數學解題中常用的思路.
例2 ?如圖3,長方體的底面邊長分別為2 cm和4 cm,高為5 cm,若一只螞蟻從P點開始經過4個側面爬行一圈到達Q點,則螞蟻爬行的最短路徑是________cm.
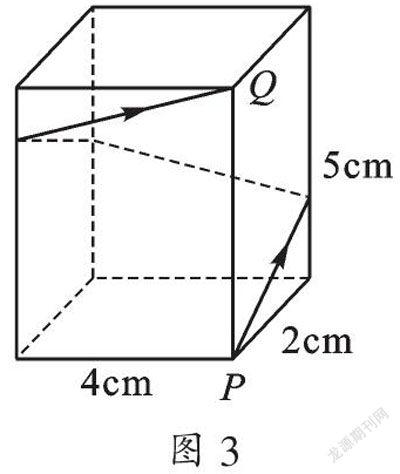
【分析】要求立體圖形中的最短路徑首先要化曲為直,即將長方體側面展開成如圖4所示,則PA=2+4+2+4=12(cm),兩點之間線段最短,利用勾股定理便可解決.

解:PA=2+4+2+4=12(cm),
∵Rt△PAQ中,∠A=90°,
∴PQ2=PA2+AQ2,
∴PQ2=122+52=169,
∵PQ>0,∴PQ=13 cm.
【點評】很多數學新問題往往是通過形或數的逐步轉化,化歸為一個比較熟悉容易的問題,從而達到解決原問題的目的.
(作者單位:江蘇省常州市武進區湖塘實驗中學)

