勾股定理中的分類討論

潘美麗

在用勾股定理解決問題時，有些問題會出現多種情況，若分析不到位就會漏解或錯解.這就需要我們利用分類思想對各種情況加以討論，并逐類求解，然后綜合得解.本文以一個中考題為例，對運用勾股定理解題時需要用到的分類思想加以探討，供同學們參考.

【例題】（2010·黑龍江雙鴨山）Rt△ABC中，∠BAC=90°，AB=AC=2. 以AC為一邊，在△ABC外部作等腰直角三角形ACD，則線段BD的長為_______.

【分析】首先要結合題意，畫出相應的圖形.因為以AC為一邊在△ABC外部作等腰直角三角形ACD，則AC可以是直角邊，也可以是斜邊，其中以AC為直角邊又分兩類，分別以A、C為直角頂點，所以有三種情況.

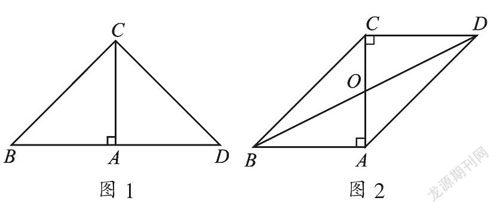
【解答】情況一：如圖1，以A為直角頂點，向外作等腰直角△DAC，

∵∠DAC=90°，且AD=AC，

∴BD=BA+AD=2+2=4.

情況二：如圖2，以C為直角頂點，向外作等腰直角△ACD，

∵△ACD是等腰三角形，

∴得AC=CD=2，

∠ACD=90°，

又∵∠BAC=90°，AB=AC=2，

∴AB∥CD且AB=CD.

∴四邊形ABCD是平行四邊形.

∴AC和BD互相平分，且相交于O，

情況三：如圖3，以AC為斜邊，D為直角頂點，向外作等腰直角△ADC，

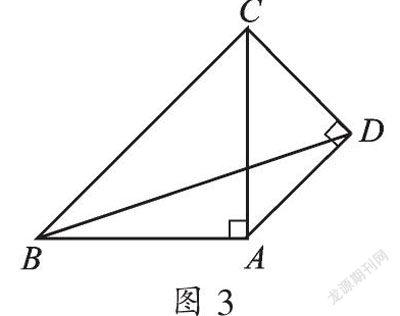
∵∠ADC=90°，AD=DC，且AC=2，

∴設AD=DC=x，

根據勾股定理，

建立方程x2+x2=22，

又∵△ABC、△ADC是等腰直角三角形，

∴∠ACB=∠ACD=45°，

∴∠BCD=90°，

又∵在Rt△ABC中，

【涉及知識點】等腰三角形，勾股定理.

【點評】本題中，符合條件的圖形不唯一，所以結論存在多種情況.在應用一條已知線段構造等腰直角三角形時，這條已知線段可以是直角邊，也可以是斜邊.根據具體圖形，結合勾股定理計算線段的長即可.本題主要考查勾股定理、等腰三角形性質的靈活運用，同時對分類討論思想有較高要求.

同學們不妨嘗試完成下列變式：

【變式】Rt△ABC中，∠BAC=90°，AB=AC=2.以BC為一邊，在△ABC外部作等腰直角三角形BCD，則線段BD的長為_______.

【分析】本例同上例類似，都是有著與勾股定理有關的無圖多解的特點.如果不注意分類討論，就會漏解或錯解.所以有必要利用分類討論思想逐類求解.

參考答案：2或4或2.

同學們不妨再想一想，如何求AD的長？

【小練習】

1. 已知△ABC是等腰三角形，其中一邊長是10，另一邊長是8，則底邊上的高為（ ? ? ?）.

D. 以上都不是

2. 某園藝公司對一塊直角三角形的花圃進行改造.測得兩直角邊長為6 m、8 m.現要將其擴建成等腰三角形，且擴充部分是以8 m為直角邊的直角三角形.求擴建后的等腰三角形花圃的周長.

【參考答案】

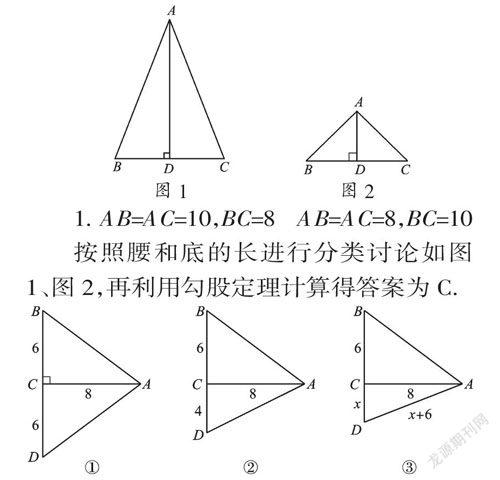
1. AB=AC=10，BC=8 ? AB=AC=8，BC=10

按照腰和底的長進行分類討論如圖1、圖2，再利用勾股定理計算得答案為C.

2. 利用等腰三角形性質進行分類討論，如圖①②③，可利用勾股定理和方程思想求得答案分別為：32或20+4

【題型分析】此類題考查了運用勾股定理計算中的分類思想.要熟悉等腰三角形的分類，要全面分析在原來直角三角形的基礎上可能構成等腰三角形的各種情況，防止以偏概全.題目如有圖形則將變得很簡單，按圖形解答即可.但若沒有圖形，則需要討論幾種可能的情況，這正是“無圖題前細思考，分類討論保周到”.

總之，勾股定理作為解題中的一種工具，在中考中的應用十分廣泛，覆蓋了填空、選擇、探究、證明等各種題型.它作為一種代數思想解決幾何問題的最重要的工具，除了在等腰三角形中出現，更是常常與其他知識，如全等三角形、圓及圖形變換等結合，同學們要能靈活運用所學知識，結合圖形的特點，恰當分類解決問題.

（作者單位：江蘇省常州市蘭陵中學）