透視數學中考題中的勾股定理應用

汪麗萍

勾股定理是幾何學中的明珠，是解直角三角形重要的定理與依據.它在生活中有著重要的應用，也是中考必考的知識點.它揭示的是直角三角形三邊的數量關系，是典型的數形結合思想的體現.下面選取中考題中的幾例作簡單的闡述，希望對同學們的學習有所幫助.

一、 直接用勾股定理計算

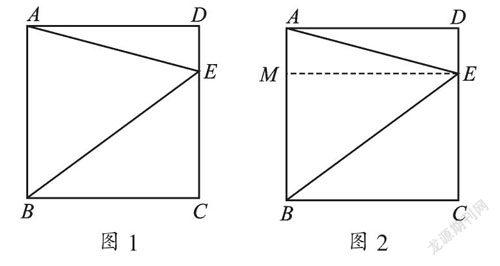
例1 ? （2015·吉林長春）如圖1，點E在正方形ABCD的邊CD上.若△ABE的面積為8，CE=3，則線段BE的長為_______.

【分析】本題根據△ABE的面積為8可求出正方形邊長為4，再根據勾股定理即可求出BE的長.

解：過E作EM⊥AB于M，如圖2，

∵四邊形ABCD是正方形，

∴AD=BC=CD=AB，∴EM=AD，BM=CE，

∵△ABE的面積為8，

∴AB×EM=8，得：EM=4，

即AD=DC=BC=AB=4，

∵CE=3，由勾股定理得：BC2+CE2=BE2，

∴BE2=42+32=25，

∴BE=5.

【點評】本題求出正方形邊長是關鍵，求出邊長后直接利用勾股定理進行計算.

二、 勾股定理和逆定理并用證垂直

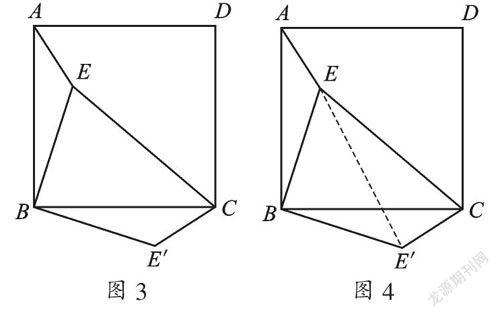
例2 ? （2013·內蒙古包頭）如圖3，點E是正方形ABCD內的一點，連接AE、BE、CE，將△ABE繞點B順時針旋轉90°到△CBE′的位置.若AE=1，BE=2，CE=3，則∠BE′C=_______度.

【分析】首先根據旋轉的性質得出∠EBE′=90°，BE=BE′=2，AE=E′C=1，進而根據勾股定理的逆定理求出△EE′C是直角三角形，從而得出答案.

解：連接EE′，如圖4，

∵△ABE繞點B順時針旋轉90°到△CBE′，

∴∠EBE′是直角，

∴△EBE′是直角三角形，

∵△ABE與△CBE′全等，

∴BE=BE′=2，∠AEB=∠BE′C，

∴∠BEE′=∠BE′E=45°，

∵EE′2=22+22=8，AE=CE′=1，EC=3，

∴EC2=E′C2+EE′2，

∴△EE′C是直角三角形，

∴∠EE′C=90°，∴∠BE′C=90°+45°=135°.

【點評】此題主要考查了勾股定理以及逆定理，根據已知得出△EE′C是直角三角形是解題關鍵.

三、 利用勾股定理解決實際問題

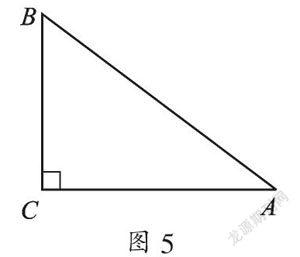
例3 ? （2015·福建廈門）已知A，B，C三地位置如圖5所示，∠C=90°，A，C兩地的距離是4 km，B，C兩地的距離是3 km，則A，B兩地的距離是_______km;若A地在C地的正東方向，則B地在C地的_______方向.

【分析】根據勾股定理來求AB的長度.由于∠C=90°，A地在C地的正東方向，則B地在C地的正北方向.

解：∵∠C=90°，A，C兩地的距離是4 km，B，C兩地的距離是3 km，

∴AB2=AC2+BC2，∴AB2=42+32=25，

∴AB=5（km）.

又∵A地在C地的正東方向，則B地在C地的正北方向.

【點評】本題考查了勾股定理的應用和方向角.這類問題的解決策略是運用勾股定理建立數學模型，把實際問題轉化為數學問題.

四、 利用勾股定理經典圖創設問題

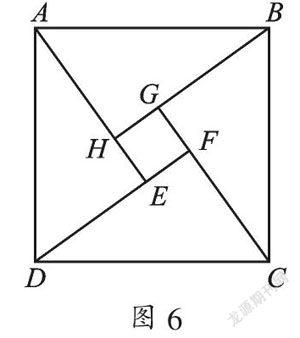
例4 ? （2015·湖南株洲）如圖6是“趙爽弦圖”，△ABH、△BCG、△CDF和△DAE是四個全等的直角三角形，四邊形ABCD和EFGH都是正方形.如果AB=10，EF=2，那么AH等于_______.

【分析】一方面根據圖形特征得出線段之間的關系AE-DE=2，另一方面利用面積關系：正方形ABCD的面積-正方形EFGH的面積=四個全等直角三角形面積和，得出AE×DE=48，再利用勾股定理得出AE2+DE2=AD2=AB2=100推出AE+DE=14，最后解二元一次方程組即可算出DE長，即AH的長.

解：∵AB=10，EF=2，

∴大正方形的面積是100，小正方形的面積是4，

∴四個直角三角形面積和為100-4=96，

設AE為a，DE為b，即4×ab=96，

∴2ab=96，a2+b2=100，

∴（a+b）2=a2+b2+2ab=100+96=196，

∴a+b=14，∵a-b=2，

解得：a=8，b=6，

∴AE=8，DE=6，∴AH=DE=6.

【點評】勾股定理有著悠久的歷史，它曾經引起很多人的興趣.本題就是在我國漢代數學家趙爽創制的弦圖的基礎上改編得到的.本題考查的就是弦圖中的各線段之間、圖形面積之間的關系和勾股定理.

（作者單位：江蘇省常州市武進區湖塘實驗中學）