船橋碰撞過程引發的沖擊動力學論題

第一作者王禮立男，教授，博士生導師，1934年生

船橋碰撞過程引發的沖擊動力學論題

王禮立1，陳國虞2，楊黎明1

(1.寧波大學機械工程和力學學院，浙江寧波315211；2. 上海海洋鋼結構研究所，上海201204)

摘要：對船橋撞擊過程引發的幾個沖擊動力學論題進行了分析。研究表明：①為降低船撞力，應采用柔性(低的結構動態廣義波阻抗)防撞裝置；②撞擊力所做的功，通過應力波傳播轉化為內能(變形能)與動能之和；而變形能中的不可逆部分愈高，防撞裝置發揮的整體作用愈大，則愈有利于防撞裝置發揮緩沖耗能作用。并且如何讓船舶盡早結束撞擊并帶走盡量多的剩余動能，應是防撞裝置設計的關鍵點；③黏性耗能可緩沖撞擊過程、延長撞擊歷時，有利于防撞裝置發揮整體作用，進而為船舶在低應力下轉向滑離、從而帶走盡可能多的剩余動能創造條件。因此，船撞橋防護裝置的設計應該建立在如下的科學設計理念上：ⅰ低波阻抗意義上的沖擊柔性，ⅱ緩沖撞擊過程意義上的粘性耗能，ⅲ防撞裝置能及早發揮整體作用，化撞擊集中力為分布載荷，以及ⅳ讓船盡早滑離而帶走盡量多的剩余動能。以鋼絲繩防撞圈為主要元件的柔性耗能防撞裝置是這一防撞理念的工程應用實例，其有效性已為工程實踐和實船撞擊試驗證實。

關鍵詞：船橋碰撞；沖擊動力學；沖擊力；能量轉換；動態響應

收稿日期：2014-01-20修改稿收到日期：2014-08-19

中圖分類號:U442文獻標志碼：A

Impact dynamics topics motivated by ship-bridge collision process

WANGLi-li1,CHENGuo-yu2,YANGLi-ming1(1. College of Mechanical Engineering and Mechanics, Ningbo University, Ningbo 315211, China；2. Shanghai Marine Steel Structure Research Institute, Shanghai 201204, China)

Abstract:Some impact dynamics topics motivated by ship-bridge collision processes were analyzed here. It was shown that (1) in order to reduce the impact force, a flexible crashworthy device with a low structural dynamic generalized wave impedance should be applied; (2) the work done by the impact force is converted via wave propagation into the internal energy (deformation energy) and kinetic energy; the larger the irreversible part of the former, the greater the overall role played by the crashworthy device, the better the buffer role played by the crashworthy device; moreover, how to make the ship as soon as possible end the collision and carry away as much as possible the remaining kinetic energy should be a key point; (3) viscous dissipation of energy can buffer the collision process, prolong the dissipation duration, help the crashworthy device to play an overall role, and create a condition for ship to end the collision; thus, the scientific design idea of a crashworthy device should be based on (i) impact flexibility with a low structural wave impedance, (ii) viscous dissipation of energy to buffer collision process, (iii) the crashworthy device to play an integral role as soon as possible to change the concentrated impact force into weaker distributed loads, and (iv) to make the ship turn away as soon as possible and take away the remaining kinetic energy as much as possible. As an engineering application example, such a design idea was reflected in a new flexible crashworthy device consisting of hundreds of steel-wire-rope coils. Its effectiveness was verified with engineering practices and real ship collision tests.

Key words:ship-bridge collision; impact dynamics; impact force; energy conversion; dynamic response

船橋相撞的危害性已經人所共知。[1-3]

如何避免或減輕船舶與橋梁相撞的災難性后果，是當前具有廣泛意義的國際性課題，日益引起各國學術界、工程界和管理部門的共同關注。

就實際工作而言，不論對于船舶設計師還是橋梁設計師，首先是如何科學地認識、分析和確定船橋撞擊力Fcq，舍此就談不上如何加強防護等等，這里用兩個下標c(代表船)和q(代表橋)來指船與橋撞擊界面處的總撞擊力Fcq。

為什么船橋撞擊力Fcq的確定會成為一個問題呢？困難在哪里呢？

從發展歷史來看，主要由于人們對它有一個由淺入深的認識發展過程。關鍵點在于：在分析船橋撞擊力Fcq時，是把船橋相撞過程看作一個準靜態平衡過程來處理，只考慮其最終平衡結果而不計及其時間過程；還是把它看作一個隨時間t變化的、沖擊動力學過程來處理。

沖擊動力學理論與固體靜力學理論的主要區別是什么呢？

概括地說，在研究沖擊載荷下結構和材料的動態響應時，通常應計及兩種基本的動力學效應以區別于靜力學分析，即結構慣性效應和材料應變率效應[4]。對結構慣性效應的考慮實質上導致了對結構中各種形式的波傳播的研究，不論是精確的還是簡化的，并促進了“結構沖擊動力學”的發展；而對材料應變率效應的考慮則導致了對材料的各種類型的應變率相關的(率型)本構關系和失效準則的研究，促進了“材料沖擊動力學”的發展。

下面就相關的主要論題作一討論。

1影響船橋撞擊力Fcq的主要因素

對于船橋撞擊力Fcq的一切分析研究，最終歸結為到底有哪些主要影響因素、以及它們如何定量地影響船撞力Fcq。只有掌握了這一點，我們才能進而提出科學的防撞措施。

就我國現行的兩個船橋撞擊力計算公式而言，如下的公路規范公式[5]本質上源自剛體整體運動的動量原理或沖量原理(Ft=Mv)，以本文統一的符號表示時為：

(1)

而如下的鐵路規范公式[6]則本質上源自船和橋作為整體但計及其結構彈性柔度的動能原理：

(2)

兩式中F(MN)為壓縮撞擊力(下標表示不同公式的出處，如GL表示公路規范，TL表示鐵路規范等)，W(MN)和M(=W/g)分別為船舶的重量和質量，v(m/s)為船舶的撞擊速度，td(s)為撞擊歷時，α為船舶與墩臺撞擊面的夾角，γ(s/m1/2)為動能折減系數，用以計及船舶動能沒有全部由橋墩所吸收，而Cu1和Cu2(m/MN)分別為船舶和橋墩的結構彈性柔度，即單位力作用下產生的位移(結構剛度ku的倒數)，Ku12是如下定義的組合剛度：

(3)

此處C和K中的下標u表示這里的結構柔度是以位移與載荷之比定義的(單位m/MN)；下文中凡是結構柔度以變形(應變)與載荷之比定義時(單位MN-1)，則以下標ε表示，以示區別。

國際上常用的船撞力公式如美國指導規范(ASHHTO)公式[7]和歐洲統一規范公式[8]等，都可以歸類于式(2)類型的公式，只是取了不同的經驗系數[9]。

對比式(1)和式(2)可見，兩者都以撞擊速度v和船舶質量M為影響船撞力Fcq的主要因素，而且兩者相同地給出Fcq正比于v，但在船舶質量M的定量影響程度上則各不相同。

用式(1)來計算撞擊力時，最大的困難在于如何正確確定撞擊歷時td。下面我們分別從準靜態分析和沖擊動力學分析兩個不同的角度來討論一下撞擊歷時。

從準靜態力學的角度來分析td時，設以U表示船橋以v相撞時的相對位移，則td的平均值可表為t=U/v，從而式(1)可改寫為：

(4a)

對于彈性系統，上式意味著：船的動能(Mv2/2)與撞擊力做功(FU/2)相等，正是動能原理的表現形式之一。而且對于彈性系統，位移U與作用力F成正比，U=CuF，正比系數Cu即彈性系統的彈性柔度(剛度Ku的倒數)。這樣，由于td=U/v=CuF/v=F/(Kuv)，式(4a)可進一步改寫為：

(4b)

當計及斜撞擊時撞擊角α的影響(sinα)，把系統的彈性柔度Cu取為船的柔度Cu1與橋的柔度Cu2之和，Cu=Cu1+Cu2，再假設船的總動能中只有β(=γg1/2)部分被橋吸收，則上式就與鐵路規范公式(式2)完全相同。在這個意義上，式(2)和式(1)是內在相通的，只是表現形式不同而已。

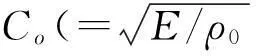
(5)

式中:ρ0為材料原始密度，E為楊氏彈性模量。把式(5)代入式(1)得

(6a)

FID=ρ0C0A0v=mC0v=

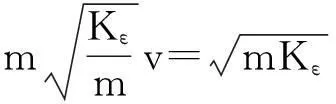
(6b)

在式(6)中已經把F的下標寫為ID以表示是由沖擊動力學(Impact Dynamics)觀點導出的。事實上，按照應力波傳播理論進行嚴格推導，將得出與式(6)完全相同的結果[3-4,9]。

對比式(4)和式(6)，可以看出準靜態分析和沖擊動力學分析對于船撞力主要影響因素的異同。為方便起見，把式(4)和式(6)的對比簡單歸納如下式所示：

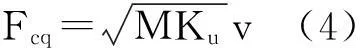
由此可見：

(1)兩種分析一致給出：船撞力正比于撞擊速度v。因此，限制船舶在臨近橋梁時的航速應是首要的防護措施之一；

(2)兩種分析都給出：船撞力正比于結構剛度的平方根，因此采用柔性防護應是首選；反之，如果片面追求橋梁/防撞裝置的高剛度高強度，則船撞力反而更大，不論對橋還是對船都更加不利；

(3)準靜態分析式(4)表示船撞力正比于結構質量M的平方根，而沖擊動力學分析式(6)表示船撞力正比于結構線密度m的平方根，并且線密度m總是與結構剛度Kε組合在一起以結構廣義波阻抗Rw的形式出現，即最終表現為：船撞力正比于結構廣義波阻抗。

關于撞擊質量M如何影響船撞力，有必要進一步討論。人們常常憑直覺或日常經驗認為：撞擊質量M應該直接影響撞擊力。想不通“船撞力怎么會與船舶總質量M無關”呢？這需要根據不同情況來分析。如果船橋相撞是一個可以忽略應力波傳播過程的準靜態過程，而且關心的是撞擊的最終結果的話，則正如式(4)所示，船的總質量M無疑是一個重要影響因素。但對于應力波傳播起主導作用的撞擊早期過程，外加載荷和撞擊能量都是通過應力波傳播而逐步作用于波陣面后方區域的，撞擊的初始峰值起著關鍵作用；這時船的總質量不會在撞擊一開始就發揮總體作用，而是隨應力波在船中傳播才逐步發揮愈來愈大的作用，因而總質量M并不直接影響瞬態初始撞擊力。

事實上，可通過一個簡化實例對這一動態過程作定量說明。考慮一個質量為M的剛體Bs(模擬船)軸向撞擊一彈性長桿Bb(模擬橋)。應力波分析表明(例如參考文獻[4]的公式(3-5))[4]，這時撞擊界面處的撞擊應力和質點速度一開始達到最大值F*，然后遵循如下的指數規律衰減：

(7a)

(7b)

式中:v*是初始撞擊速度，F*(=-ρ0C0A0v*)是相應的初始峰值撞擊力，Mt(=ρ0C0A0t)代表t時刻桿中應力波波陣面所掃過的那部分桿的質量，無量綱質量因子Rm(=ρ0C0A0t/M)則代表波陣面所掃過部分的質量Mt與撞擊物總質量M之比，它是隨時間增大的。上式表示，應力波和質點速度波的波剖面表現為一強間斷波陣面前沿(峰值)及隨后的呈指數衰減的波尾。從這里可以定量地理解總質量M在應力波傳播過程中所起的作用：撞擊一開始(t=0)的初始最大撞擊力取決于撞擊速度和波阻抗，與M無關；但此后通過時間相關的無量綱質量因子Rm(=ρ0CweAt/M)，總質量M對于應力波剖面指數衰減的快慢有影響，但隨時間其影響又逐漸減弱。

對于剛度K的影響也有必要作補充討論。式(4)和式(6)都表明，結構剛度愈大，撞擊力愈大。基于這一分析，人們已經愈來愈傾向于設計建造“柔性”防護裝置。但怎么來評價防護裝置的柔性呢？是不是具有一定結構柔度的防護裝置都是“柔性”防護裝置？都能降低撞擊力？對此，我們從基于應力波理論的式(6)出發來評價：

(1)首先，就船撞力的沖擊動力學分析而言，柔性防護裝置的“柔度”應該更嚴格地理解為“結構廣義波阻抗Rw”，或簡稱為“沖擊柔度”，而并非一般結構靜力學意義上的柔度(1/K)。這樣，“柔性防護裝置”實際上應該指“結構廣義波阻抗Rw”低的防撞裝置；

(2)其次，“結構廣義波阻抗Rw”的高低是相對而言的，嚴格地說，只有防護裝置的“結構廣義波阻抗”Rws小于船的“結構廣義波阻抗”Rwb時，才能發揮降低撞擊力的作用；

(3)再次，結構廣義波阻抗包含的有關材料參數都應該是計及應變率效應的，即指高應變率下的“結構動態廣義波阻抗”。

強調這三點，不僅有利于正確認識和科學設計“柔性”防護裝置，同時也是對今后柔性防護裝置(包括其元件)進一步研制發展提出的新挑戰。

特別應該指出，式(6)是為了說明應力波效應而把船舶簡化為“均質等截面桿”時得出的理論解，式中的廣義波阻抗Rw(=ρ0C0A0)所包含的ρ0C0取決于材料特性，而A0反映了結構特性。實際的船舶結構要復雜得多，如何確定實際船舶在沖擊載荷下等效的“結構廣義波阻抗”，是一個設計師們面臨的新課題。對于給定的船型，在采用計及應力波效應的動態數值模擬計算時，已經隱式地包含了船舶“等效結構廣義波阻抗”的分析。目前尚未見到為改進船舶抗撞功能而主動對其“等效結構廣義波阻抗”進行分析研究和設計的報道，這應是一個有待深入研究的新課題。

綜上所述，在應力波傳播起主導作用的船橋撞擊過程中，撞擊一開始的峰值撞擊力主要取決于撞擊速度v和動態結構廣義波阻抗Rw，船的總質量(重量)則隨著應力波的傳播和相互作用而逐漸產生影響。為降低船撞力，應該采用以低于船的“結構動態廣義波阻抗Rw”為特征的“柔性防護裝置”。

2影響船橋相撞過程中能量交換的主要因素

從能量/動量交換的角度看，船橋相撞的過程是一個船與橋在短歷時內進行能量/動量傳遞和交換的動力學過程。

按照傳統的彈性系統準靜態力學分析，不論是中國公路規范公式(式1)還是鐵路規范公式(式2)，實質上都如式(4a)所示那樣，把船橋相撞的動量/能量交換關系歸結為船的總動能(Mv2/2)轉化為撞擊力的做功(FU/2)，而相應的能量守恒關系則表現為：船的總動能最終轉化為船和橋的總變形能(內能)。以50 000 t船舶為例，如果船速以4 m/s計，則相應的總動能高達約300 MJ。對于這么巨大的動能，如果其全部或大部分要由被撞橋梁的局部受損區在短歷時內來承受，又不至于導致安全事故，那無疑是一個極其嚴峻的挑戰！

從沖擊動力學的觀點來分析這一能量/動量交換關系時，與上述的準靜態力學分析相區別，應強調以下兩點動力學效應。

(1)其一是：能量傳遞和交換不是整體結構在瞬時立即完成的，而是通過應力波的傳播過程逐漸發生的，具體的能量轉換形式則需要考察跨過波陣面的能量守恒關系，并視不同材料和結構特性而異。

(2)其二是：沒有理由預先限定撞擊的終態必定對應于“船的總動能最終轉化為船和橋的總變形能(內能)”；恰恰相反，既然這是一個經由應力波傳播進行能量交換的過程，我們可以期望或設法在交換了總撞擊能量中盡可能低的百分比后就能結束(脫離)撞擊。這從根本上對于船和橋的安全防護都將是極有利的。下面對這兩點分別作進一步分析。

具體地說，當經由應力波以波速D傳播而發生能量交換時，應該滿足如下的跨過波陣面的能量守恒條件(例如參看參考文獻[4]的式(2)-61和式(2)-62)[4]：

(8)

此處應力σ以拉為正，質點速度v以坐標正向為正，e是材料單位質量的內能(或ρ0e是單位體積的內能)，Δ表示跨過波陣面的相關量的差值，并以上標-和+分別表示波陣面前方和后方的各量。式(8)第一式等號左邊的負號對應于右行波，正號對應于左行波。式(8)第一式的物理意義是：在應力波以波速D傳播的過程中，當波陣面在dt時間傳播過dX(=Ddt)距離的質量時，應力σ所做的功轉化為兩部分能量：內能(即變形能)和動能(正是動能部分在準靜態分析中被忽略了)；而式(8)第二式的物理意義是：內能即變形能。

為方便計，下面討論波陣面前方處于靜止的零應力狀態(σ+=v+=ε+=e+=0)的情況，則式(8)化為：

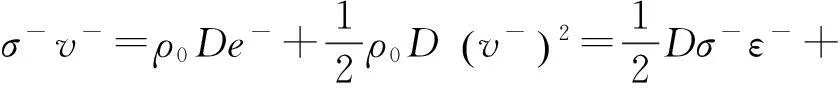
(9)

對于線彈性系統，彈性波速D=Ce=(E/ρ0)1/2。當把跨過波陣面的動量守恒條件σ-=?ρ0Cev-和連續性條件v-=?Ceε-分別代入式(9)第一式等號右邊動能項中的(v-)2，即可證明式(9)第一式中的動能項剛好等于內能項[8-9]，即：

換句話說，如圖1所示，由波陣面掃過的那部分質量所吸收的總能量中，動能形式和內能形式的能量相等，各占總能量的一半。在傳統的準靜態分析中，認為撞擊力所做的功都轉化為變形能(內能)，而沒有考慮到不可忽略的、與內能等量的動能，這正是用準靜態分析來研究沖擊動力學動態問題中的能量交換時之不足之處。

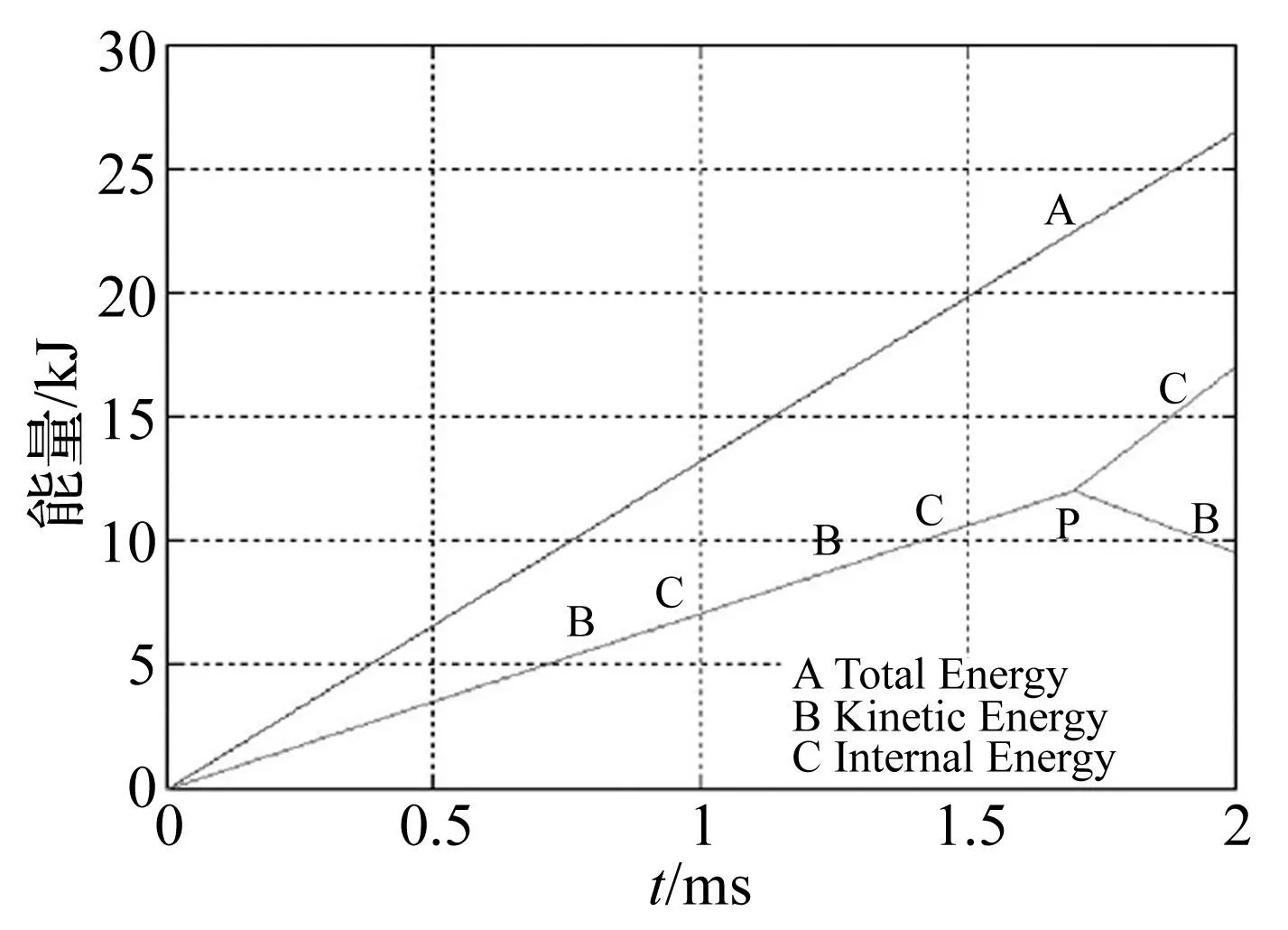
圖1　跨過彈性波波陣面的能量分配隨時間的變化 Fig.1 Energy allocation across the elastic wave front changes with the time

圖1中的P點對應于彈性波傳播到達固定端，由于固定端邊界條件對應于位移和質點速度為零，受此條件的約束，動能被釋放而轉化為變形能。此后，隨著反射波在固定端的反射傳播，動能隨時間進一步減少，而變形能則隨時間進一步增大。

對于彈性-線性硬化塑性情況，設彈性模量為E和塑性線性硬化模量為Ep(?E)。撞擊引起的應力波將“分裂”成兩部分[4]：以較快的彈性波速Ce(=(E/ρ0)1/2)傳播的彈性前驅波，和后隨的以較慢塑性波速Cp(=(Ep/ρ0)1/2?Ce)傳播的塑性波。對于彈性前驅波，如前所述，動能和內能各占總吸收能量的一半。對于后隨的塑性波，經過與推導式(10)相類似于的分析和數學運算后可以發現[9-10],由于塑性變形的不可逆性，塑性波的比內能 (ρ0e-)p不再與塑性波的動能(ρ0(v-)2/2)p相等，其差值為：

(11)

可見通過塑性波傳播進行能量傳遞時，所吸收的總能量中內能(變形能)部分大于動能部分，內能(變形能)部分中包括可恢復的彈性應變能和不可恢復(耗散)的塑性應變能。

應該強調：對于具有彈塑性特征的大多數金屬材料，如上所述，撞擊引起的應力波將“分裂”成以較快的彈性波速Ce(=(E/ρ0)1/2)傳播的彈性前驅波，以及后隨的以較慢塑性波速Cp(=(Ep/ρ0)1/2?Ce)傳播的塑性波。由于塑性波速通常比彈性波速小一個量級，撞擊過程結束時塑性波到達的區域有限，這就是為什么撞擊造成的塑性區常常集中在高度局域化的小范圍。然而，如果一個防撞裝置只有局域化的小范圍發揮耗能作用，不論從技術角度、還是從經濟角度，都是不可取的。顯然，一個科學而經濟的防撞設計應該追求防撞裝置發揮整體的吸能/耗能作用,這時不僅防撞裝置整體起到了吸能/耗能作用，而且還起到了把局域化的高強度集中撞擊力轉化為較弱的分布載荷的作用。

從以上分析可見，任一防撞裝置的能量吸收功能中，一般包含可恢復能量和不可恢復能量(耗能)。如果吸收的全部是彈性的可恢復能量，能量形式只會隨著具體邊界條件而轉化，而不會有任何耗散。例如當邊界條件為零應力條件(自由端)時，可逆變形能將被釋放而轉化為動能。顯然，任一高效的防撞裝置，不僅應該起到降低撞擊力的作用，把較強的集中撞擊力轉化為較弱的分布載荷，而且應該讓防撞裝置整體(而不是局域化范圍)起到耗散撞擊能量的作用，從而能夠通過防撞裝置盡可能地減少傳遞給橋梁的撞擊能量。

其實，如本節一開頭所說，更為重要的是：船橋相撞時應盡最大可能使船和橋及早脫離接觸，以盡可能減少撞擊過程所交換的能量，此乃保護船橋安全的上上之策。猶如坦克裝甲板設計成能使“反坦克彈”發生迅速“滑彈”那樣，如果能在船橋相撞時讓船舶盡可能早地滑離防撞裝置，從而使得船舶總動能中盡可能少的百分比參與撞擊過程的能量交換，應該成為我們的追求目標。還應該注意，船舶滑離防撞裝置的過程在沖擊動力學分析上相當于處理具有移動沖擊載荷邊界條件的復雜問題，使得應力波效應扮演主導作用的歷時進一步延長而更加不可忽略。

圖2　撞擊角φ=45°時船和橋墩相對位置 Fig.2 Ship-bridge collision in the case of φ=45°

圖2給出一個已應用于廣東湛江海灣大橋的實例[11-12]。該柔性耗能防撞裝置以鋼絲繩防撞圈為主要元件，其外鋼圍在迎撞面的一側設計成90°夾角的楔形結構，使得船軸線與外鋼圍迎撞面的碰撞角φ為45°夾角。由于撞擊力的方向一般不通過船的質心，必然對船施加了一個力矩，從而促使船的轉動而改變航行方向，沿著外鋼圍滑開。動態數值計算表明：在大約時間t=4.4 s時，撞擊力F(t)幾乎降為零，表明船與防撞裝置脫離，撞擊完全結束。

相應地，撞擊過程中系統的能量分配及其隨時間的變化如圖3所示。圖中曲線C代表系統的總能量(撞擊前的船舶總動能)，曲線A代表系統的動能，曲線B代表系統的內能(變形能)。顯然，在撞擊過程中船舶的動能減少，轉變為系統的動能和變形能，其中，大部分轉換為船和防撞裝置的變形能(曲線B)，另一部分轉變為曲線D所代表的滑動能。A、B、D三曲線之和與C曲線之差反映了計算中的砂漏能，在本例中幾乎可以忽略不計。

本例表明，采用這一新型柔性耗能防撞裝置后，船舶動能在撞擊前后的變化不大(約50 MJ)，僅占船舶總動能(307 MJ)的約16 %。這意味著船在轉向并脫離碰撞后把大部分沖擊能量以剩余動能形式帶走了(占船舶初始動能的80%以上)。這是避免船橋兩敗俱傷的關鍵所在。對變形能的具體計算還表明，其中防撞裝置所吸收的達到約22 MJ，船舶變形所吸收的達到約8.5 MJ，分別占船舶初始動能的7.2%和2.8%左右，都不高，且前者大于后者，說明防撞裝置發揮了“吸能/耗能器”的作用，既保護了橋、也保護了船舶免遭嚴重破壞。

從以上分析可見，撞擊過程中的能量交換的形式和多少、以及參與能量轉換的質量的多少，都隨波傳播過程而變化發展。撞擊力所做的功，通過應力波傳播通常轉化為內能(變形能)與動能之和，其可逆部分的能量形式視反射邊界條件的不同可相互轉換；而變形能中的不可逆部分愈高，防撞裝置愈能發揮整體吸能/耗能作用，則愈有利于防撞裝置發揮緩沖耗能作用。在船橋相撞過程中如何讓船舶盡可能早地滑離防撞裝置，帶走盡可能多的剩余動能，從而盡可能地減少撞擊能量交換，乃是防撞裝置設計的關鍵性要點之一。

A-動能，B-內能 (變形能)，C-總能，D-滑動能。 圖3　撞擊角φ=45°時系統能量-時間曲線 Fig.3 Curves of energy vs. time calculated in the case of φ=45°

3黏性耗散在船橋相撞過程中的作用

從上一節能量轉換的角度來看，彈性系統在撞擊過程中只吸收能量而并不耗散能量，其所吸收的能量都是可恢復的。由此不難想象，如果防護裝置具備耗能特性，能經由防護裝置耗散掉盡可能多的沖擊能量，顯然更有利于橋梁和船舶的安全。

就耗能類型而言，通常可劃分為塑性耗能和黏性耗能兩類。前者通過結構/材料的不可逆塑性變形起到耗能作用，后者則通過結構/材料的不可逆黏性流動起到耗能作用。

由鋼結構為主組成的彈塑性防撞裝置(如目前常用的鋼套箱結構等)是塑性耗能防撞裝置的典型代表。對于這類耗能防撞裝置，有以下三點值得注意：

(1)首先，由于鋼的波阻抗高，并且只有在超過屈服強度的高載荷下才會發生塑性耗能，所以從沖擊動力學角度看，難以實現真正的低撞擊力、即相對于船舶結構而言的低波阻抗意義上的“柔性防撞”。

(2)其次，鋼的塑性波速通常比其彈性波速小一個量級，因此鋼結構防撞裝置在經受船撞時，容易形成高度局域化的塑性變形區，不能充分發揮整個防撞裝置的作用。尤其是一旦形成高度局域化的塑性變形撞擊區，船頭容易鑲住在局部撞擊區而難以滑離，于是船舶總動能將自始至終、百分之百地參與撞擊過程的能量交換，這對船橋安全防護是最不利的！

(3)再次，塑性耗能伴有不可逆的塑性殘余變形，防撞裝置每經受一次撞擊就要進行修復，更換已發生殘余變形的元件，不能重復使用。

鑒于塑性耗能防撞裝置上述三點先天性的不足之處，人們遂傾向于探索基于不可逆黏性流動的黏性耗能防撞裝置。那么黏性流動耗能機制對于船橋相撞過程的應力波傳播和相應的能量交換有什么樣的影響呢？

我們先來考察一下黏性耗能特性對于應力波傳播和撞擊力的影響。為了便于從原理上對黏性效應加以揭示和說明，考慮一個簡化的“短彈性桿Bs-黏彈性阻尼層Bd-長彈性桿Bb”組成的具有黏性耗散的非彈性系統，即短桿Bs以速度v撞擊前端帶有阻尼層Bd的長桿Bb，如圖4所示。黏彈性阻尼層的的動態力學響應采用圖4(b)所示的三單元黏彈性模型來描述，即由一個彈性模量為E的彈簧元件和一個Maxwell元件并聯組成，后者由彈性模量為EM的彈簧元件和松弛時間為θM的黏壺元件串聯組成。相應的黏彈性本構關系由下式描述[4]

(12a)

或其微分形式：

(12b)

圖4　黏彈性耗能系統示意圖 Fig.4 Schematic of a visco-elastic energy-dissipating system

下面采用動態LS-DYNA數值計算對相關的應力波傳播特性和撞擊力進行分析。

數值計算中，鋼制有限長桿Bs的有關材料參數取為：密度ρ0=7.85×103kg/m3, 彈性模量E=210 GPa, 泊松比n=0.3 因而波速Cwe=5.17 km/s 及波阻抗ρ0Cwe=40.6 MPa s/m。桿Bb的材料設為三種：①剛體(ρ0Ce=∞)，②與撞擊桿Bs相同的鋼，③混凝土，有關材料參數為ρ0=2.50×103kg/m3,E=25 GPa,υ=0.17因而Ce=3.16 km/s 及ρ0Ce=7.9 MPa s/m。黏彈性阻尼層的有關材料參數則參照對于有機玻璃動態力學特性的實驗研究結果[4],取為密度ρ0=1.19×103kg/m3，三單元黏彈性模型中并聯彈簧的彈性模量E=2.94 GPa，并聯Maxwell元件的串聯彈簧EM=3.07 GPa 而串聯黏壺的松弛時間θM=95.4 μs，從而有特征波速Cw=((E+EM)/ρ0)1/2=2.25 km/s以及瞬時波阻抗ρ0Cw=2.68 MPa s/m。這時，鋼桿Bs波阻抗與黏彈性阻尼層波阻抗之比ns-d= 15.1，此值愈高意味著黏彈性阻尼層的沖擊柔性愈低，而其耗散特性則主要由黏彈性松弛時間θM來刻畫，這可以通過以下的算例來理解。

撞擊桿Bs與黏彈性阻尼層Bd撞擊界面處撞擊力的計算結果匯總在圖5a中，而相應的沒有黏彈性阻尼層時的計算結果則給出在圖5(b)中(曲線1，2，3)，以供比較。

由圖5可見幾點主要結果：

(1)不論有沒有黏彈性耗能阻尼層，撞擊力的高低依賴于桿Bs與桿Bb的波阻抗之比，在上述三種不同情況中，以Bb為剛性材料時為最高，而以Bb為混凝土材料為最低。這意味著橋墩的波阻抗低，則撞擊應力就低。此結果與本文第一節的分析一致。

(2)但不論上述Bb三種不同情況中的哪一種，添加了低波阻抗的黏彈性耗能阻尼層后，撞擊應力都顯著地、甚至于成倍地降低。

(3)尤其是，伴隨著黏性能量耗散，不論是加載波還是卸載波，都不再像無黏彈性耗能阻尼層的彈性波那樣(圖5(b)中曲線1，2，3)顯示無緩沖的“瞬態響應”，而顯示一種低應力下伴隨阻尼耗散的緩沖遲滯過程，從而使低應力下的撞擊歷時大大延長。在圖5(b)中，黏性效應導致的應力波作用歷時延長了近一個量級，使得應力波傳播效應更加不可忽略。這種在應力波傳播過程中的緩沖遲滯效應對于船橋相撞而言，從開始撞擊到隨后的脫離撞擊都將起到十分有益的緩沖作用。

圖5　撞擊應力的計算結果 Fig.5 Impact stresses calculated

上述原理性分析說明，采用低波阻抗黏性耗能防護裝置既可以明顯降低撞擊力，同時還可以緩沖撞擊過程、延長撞擊歷時。不難想象，只要在防撞裝置設計中能使船偏離航向，那么在低撞擊力下延長撞擊歷時將給船舶提供足夠時間轉變其航行方向，從而創造條件讓船舶帶走盡可能多的剩余動能，更加有利于橋梁和船舶的安全。

下面再來考察一下黏性耗能特性對于撞擊能量轉換與分配的影響。

由于黏彈性波傳播的復雜性，其傳播過程中的能量轉換與分配已難以用類似于式(10)和式(11)那樣的解析式來描述。下面借助于一個實例的數值計算來分析。考慮一長為3 m的黏彈性桿，一端受恒速v撞擊，另一端為固定端(位移和質點速度為零)。材料參數與前面討論圖4中黏彈性阻尼層Bd時所采用的相同。

圖6給出了通過黏彈性波傳播所吸收的總能量中內能與動能的分配。

如令此黏彈性材料的松弛時間θM=∞，就化為相應的彈性波問題，那就是圖5所示結果。對兩者進行對比，可看到黏彈性波與彈性波在能量轉換與分配中的差別。

由圖可見，與彈性波時內能總等于動能(圖5)的情況不同，在黏彈性材料的情況下，黏彈性桿所吸收的總能量中內能(曲線C)大于動能(曲線B)，并且由于耗散特性，其差別隨時間增加。在本算例中，時間約為1.7 ms時入射波到達固定端。受到固定端位移和質點速度為零的約束，這時動能開始釋放并轉化為內能。此后動能隨時間繼續減少，而內能隨時間進一步增大。這是一種由于固定端邊界條件所引起的能量形式的內部轉換。

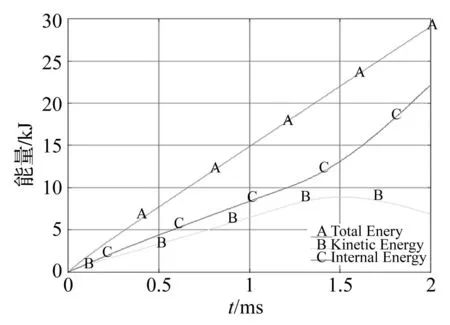
圖6　黏彈性波能量分配計算結果 Fig.6 Energy allocation calculated for visco-elastic waves

在分析了黏性耗能對于撞擊力和撞擊能量轉換的影響之后，現在可以設想一下如下兩種不同情況的物理圖像：一條船分別撞擊一個彈簧和一個圖4(b)所示黏彈性元件。當撞擊在彈簧元件上時，撞擊力的時程曲線將如圖5(b)中的曲線1，2，3所示那樣，加載和卸載都呈現無延遲的瞬時響應，而且卸載后，彈簧吸收的能量沒有耗損，會全部釋放。但當撞擊黏彈性元件時，撞擊力的時程曲線將如圖5(a)所示那樣，加載和卸載都呈現延遲的非瞬時響應(參見圖5(b)中的對比)，特別是即使載荷開始卸降了，變形還會繼續；并且由于在加-卸載過程中有能量耗損，黏壺阻尼器所吸收的能量在卸載后只會釋放一部分。人如果跟著船舶一起撞擊這兩種元件，在撞擊彈簧元件時會有一種突發的沖擊感，而在撞擊黏壺阻尼器時則會有一種延遲的緩沖感。這種緩沖效應不僅有利于降低和緩沖船橋相撞開始時的撞擊力，而且有利于緩沖船橋脫離撞擊時的卸載載荷，以免船舶轉頭太快時有可能造成船尾對橋的二次撞擊。

還應該指出，黏性耗能防撞裝置與塑性耗能防撞裝置相比，由于黏彈性波的傳播速度與彈性波相同，有助于防撞裝置整體發揮耗能作用；而塑性波的傳播速度比彈性波小一個量級，容易形成高度局域化的塑性變形區，不利于發揮防撞裝置的整體耗能作用。

當然，由于黏彈性波傳播的應變率相關性，黏性耗能防撞裝置的設計遠比無黏性防撞裝置復雜得多。黏性效應顯著與否主要與刻畫沖擊條件下黏性效應的“高頻松弛時間”θ2的數值大小有關(式12)。事實上，表征黏彈性材料黏性特性的任一松弛時間參數θj(j=1,2,3…)，各自都只對應一個有效的應變率(或時間)影響區，此“有效影響區”，不論以時間表示還是以應變率表示，均為大約4.5個量級[4]。此相對應地，就黏彈性波的傳播而言，存在一個由θ2起主要作用的、或即以“有效傳播時間”teff=θ2，或“有效傳播距離”Xeff=Cvθ22占統治地位的轄區。超出這一“有效傳播時間”或“有效傳播距離”占統治地位的轄區，θ2就不再發揮顯著的影響作用。因此，如果防撞裝置的等效松弛時間選擇得不適當，甚至于可能在某些情況下，設計者會在數值計算中發現黏性耗能不大，黏性緩沖效應不明顯。這時就要調整防撞裝置的等效松弛時間。如何調整和制造出具有不同松弛特性的防撞裝置，是今后需要進一步研究解決的課題。

綜合以上分析可知，船撞橋防護裝置的設計應該建立在低波阻抗意義上的沖擊柔性和緩沖撞擊過程意義上的黏性耗能的設計理念上，一方面可以降低船撞力，另一方面由于黏性耗能機制可以緩沖撞擊過程、延長撞擊歷時，有助于防撞裝置發揮整體作用，并為船舶在低應力下轉向滑離創造條件，從而帶走盡可能多的剩余動能，達到既保護橋又保護船、并盡可能使防護裝置能夠反復使用的目的。圖2所示的以鋼絲繩防撞圈為主要元件的柔性耗能防撞裝置正是按照這一防撞理念研發的工程應用的實例。實船撞擊試驗證實了這一防撞理念是正確和有效的[13]。

4結論

對于船橋撞擊過程中相關的幾個沖擊動力學論題進行了分析，得出幾點主要結論：

(1)在應力波傳播起主導作用的船橋撞擊過程中，撞擊一開始的峰值撞擊力主要取決于撞擊速度v和結構動態廣義波阻抗Rw，船的總質量則隨著應力波的傳播和相互作用而逐漸產生影響。為降低船撞力，應該采用以低于船的“結構動態廣義波阻抗Rw”為特征的“柔性防護裝置”。

(2)在船橋撞擊的能量交換過程中，其能量交換的形式和多少、以及參與能量轉換的質量的多少，都隨波傳播過程而變化發展。撞擊力所做的功，通過應力波傳播而轉化為內能(變形能)與動能之和，其可逆部分的能量形式視反射邊界條件的不同可相互轉換；而變形能中的不可逆部分愈高，防撞裝置發揮的整體作用愈大，則愈有利于防撞裝置發揮緩沖耗能作用。在船橋相撞過程中如何讓船舶盡可能早地滑離防撞裝置，帶走盡可能多的剩余動能，從而盡可能地減少撞擊能量交換，應是防撞裝置設計的關鍵性要點。

(3)兼備柔性和黏性耗能特性的防護裝置，一方面可以降低船撞力，另一方面黏性耗能機制可以緩沖撞擊過程和延長撞擊歷時。這既有助于讓防撞裝置發揮整體作用，達到整體發揮吸能/耗能作用，并把較強的撞擊集中力轉化為較弱的分布載荷；又為船舶在低應力下轉向滑離創造條件，從而帶走盡可能多的剩余動能，達到既保護橋又保護船、并盡可能使防護裝置能夠反復使用的目的。

(4)概而括之，船撞橋防護裝置的設計應該建立在如下的科學設計理念上：①低波阻抗意義上的沖擊柔性，②緩沖撞擊過程意義上的黏性耗能，③防撞裝置能及早發揮整體作用，化撞擊集中力為分布載荷，以及④讓船盡早滑離而帶走盡量多的剩余動能。圖2所示的以鋼絲繩防撞圈為主要元件的柔性耗能防撞裝置正是這一防撞理念的工程應用實例，其有效性已為多年的工程實踐和大型實船撞擊試驗所證實。

參考文獻

[1]Jones N.Structural aspects of ship collisions. in jones N and wierzbicki T, editors. structural crashworthiness[M]. Butterworths Publishers, London and Boston, 1983:308-337.

[2]陳國虞，王禮立. 船撞橋及其防御 [M]. 北京：中國鐵道出版社，2006.

[3]陳國虞，王禮立，楊黎明，等. 橋梁防撞理論和防撞設施設計 [M]. 北京：人民交通出版社，2013.

[4]王禮立. 應力波基礎 [M].第二版．北京：國防工業出版社出版，2005.

[5]中華人民共和國交通部. 公路橋涵設計通用規范[S].(JTG D60-2004)，2004.

[6]中華人民共和國鐵道部. 鐵路橋涵設計基本規范[S].(TB10002.1-2005)，2005.

[7]AASHTO. Guide specifications and commentary for vessel collision design of highway bridges[S]. American Association ofState Highway and Transportation Official, Washington D. C., 2009.

[8]Vrouwenvelder A C W M. Design for ship impact according to eurocode 1, Part 2.7, Ship collision analysis[R].Rotterdam: Balkema A A, 1998: 123-134.

[9]王禮立，楊黎明，陳國虞，等，船橋相撞時撞擊力和能量轉換的沖擊動力學分析[C].第二十屆全國橋梁學術會議論文集(下)，2012，武漢:921-935.

[10]Wang Li-li, Yang Li-ming, Tang Chang-gang,et al. On the impact force and energy transformation during ship-bridge collisions[J]. International Journal of Protective Structures,2012,3(1):105-120.

[11]王禮立, 張忠偉, 黃德進, 等. 船撞橋的鋼絲繩圈柔性防撞裝置的沖擊動力學分析[M]. 見:洪友士. 應用力學進展—祝賀鄭哲敏先生八十華誕. 北京: 科學出版社, 2004: 172-180.

[12]Wang Li-li, Yang Li-ming, Huang De-jin, et al. An impact dynamics analysis on a new crashworthy device against ship-bridge collision[J]. International Journal of Impact Engineering, 2008, 35(8): 895-904.

[13]楊黎明，呂忠達，王禮立，等，橋梁抗船撞柔性防護方法及實船撞擊實驗[C].第二十屆全國橋梁學術會議論文集(下)，2012，武漢:948-954.