奇異譜分解在超聲速無人機聲振試驗數據處理中的應用

第一作者劉鎏男，博士生，1986年生

通信作者閆云聚男，教授，1954年生

奇異譜分解在超聲速無人機聲振試驗數據處理中的應用

劉鎏，閆云聚，李鵬博

(西北工業大學力學與土木建筑學院，西安710072)

摘要：將相空間重構和奇異譜分解相結合對受強氣動噪聲影響的超聲速飛行器測試數據進行濾波,以實現對于試驗參數的精確識別。首先通過數值仿真論證該方法的可行性,然后針對某型超聲速無人機的聲振試驗對試驗采集數據進行相空間重構,并對重構后的軌跡矩陣進行奇異值分解,得到反映真實信號信息的信號子空間和反映噪聲信息的噪聲子空間。通過定義奇異值差分譜這一指標來判定真實信號信息子空間維數,并針對現有最大差分譜理論缺陷提出了優選差分譜峰值理論,利用奇異譜分解的逆過程對真實信號進行重構。重構結果表明,該方法適用于超聲速飛行下的飛行器聲振試驗數據處理,為超聲速飛行器飛行狀態的精確描述提供了良好的思路。

關鍵詞：相空間重構；奇異值分解；超聲速；聲振試驗；信號濾波

收稿日期：2013-12-11修改稿收到日期：2014-01-11

中圖分類號:TB53文獻標志碼：A

Singular value spectral decomposition and its application in acoustic vibration test data processing of a supersonic aircraft

LIULiu,YANYun-ju,LIPeng-bo(College of Civil Engineering and Mechanics, Northwestern Polytechnical University, Xi’an 710072, China)

Abstract:In order to realize precise identification of acoustic vibration test data of a supersonic aircraft, a new filtering method combining phase space reconstruction and singular spectral decomposition was proposed. Firstly, the feasibility of this method was demonstrated through numerical simulation. Secondly, in order to separate the signal subspace and the noise subspace, the phase space reconstruction of the test data was conducted, and the attractor track matrix was also decomposed with singular value decomposition (SVD). Finally, aiming at shortages of the maximum difference spectrum theory, the concept of optimizing difference spectrum theory was presented, and the signal reconstruction was proposed on the basis of the peak position of the optimizing difference spectrum. Reconstruction results showed that the proposed method is suitable for processing the acoustic vibration test data of a supersonic aircraft, the result provided a good foundation for the precise description of a supersonic aircraft’s flying state.

Key words:phase space reconstruction; singular value decomposition; supersonic; acoustic vibration test; signal filtering

超聲速飛行器在高速飛行時,所形成的復雜氣動流場會產生強大的氣動噪聲,并且有可能與飛行器結構體形成嚴重的耦合振動效應。飛行器結構殼體外面的強大氣動噪聲和其自身的強烈振動都會傳遞到飛行器儀器設備艙內,使內部的儀器設備處于強烈的振動與噪聲環境中,對設備造成的可能危害包括：導線擦傷、緊固件松動、間斷電觸點、帶電元件的接觸和短路、密封失效、構件疲勞、光學上的失調、裂紋和斷裂、微電子元件線路故障、導線的磨損、印刷電路板破裂等各種故障,將嚴重影響飛行器飛行的可靠性與安全性。為了預防以上可能的危害并進一步準確預示飛行器儀器設備的振動噪聲環境,需要進行聲振試驗從而對噪聲環境下的飛行器振動響應進行預報。試驗中振動響應數據的獲取不可避免地存在各種干擾,造成諸如測試數據模糊,信噪比低,信號突變等問題,直接影響到后續的數據處理和試驗理論論證對比分析。因此,如何選取適當的信號濾波方法對試驗數據進行預處理就顯得尤為重要。

近幾年來奇異譜分解技術(Singular Value Decomposition, SVD)被廣泛運用。張友民等[1-2]和宮曉琳等[3]將基于SVD的固定區間平滑方法應用于機載合成孔徑雷達運動補償用位置姿態系統的后處理,獲得了位置、速度和姿態的最優估計;Shim等[4]和賈鵬等[5]將基于SVD的冗余慣導系統故障診斷方法用于雙陀螺故障檢測;Shnayderman等[6]和朱衛綱等[7]提出了基于SVD的遙感圖像融合性能評價,較好地反映了多類遙感圖像融合的質量。何田等[8-10]將SVD運用于噪聲背景下突變信息的檢測,實現了對于某型航空發動機碰摩故障實測數據的處理。

SVD是一種非線性的濾波方法,它克服了傅里葉變換只能處理平穩信號的局限性，不需要像小波分析那樣耗時耗力的憑借經驗選擇小波函數,也沒有Hilbert-Huang變換所存在的邊界處理以及模態混疊等問題，與上述方法相比,它具有濾波算法簡單,濾波能力強以及頻域范圍普適性等優點。過往的一些關于SVD方法的研究往往集中于對一些中低頻信號進行研究,信號本身較為簡單且所處環境亦較為單一,少有關于SVD方法運用于復雜環境下振動測試數據處理的相關研究。鑒于此,本文在以往研究的基礎上,將SVD方法和相空間重構相結合對超聲速飛行器聲振試驗數據進行處理。

1相空間重構與奇異值分解

對于一系列離散時間序列{hi,i=1,2,…,N},其中N為采樣點編號,利用Takens定理[11]可以對其進行相空間重構,得到如下L×K階Hankel矩陣：

(1)

其中：K=N-L+1,延時值為1,H也被稱為軌跡矩陣。

軌跡矩陣H經SVD分解后可得如下形式：

H=UΣVT

(2)

式中：U∈RL×L，Σ是一個L×K的對角陣,Σ=diag(σ1,σ2,…,σn)，σ1,σ2,…,σn為奇異值且按降序排列,V∈RK×K。

式(2)兩邊同時右乘V,有

HV=UΣ

(3)

當離散時間序列{hi,i=1,2,…,N}含有噪聲時,軌跡矩陣H作SVD分解后可表示為：

UsΣsVTs+UωΣωVTω

(4)

由式(4)可以看出,軌跡矩陣經奇異值分解以后,得到了表征信號信息的信號子空間H′和表征噪聲信息的噪聲子空間N,這兩個空間是互不相關的,SVD分解的目的就是將這兩個互不相關的子空間分離以達到信號濾波的作用。

2相空間重構維數和最小嵌入維數確定

2.1相空間重構維數確定

前文已經提到,只有在由一維觀測序列及其適當延時值所構成的維數合適的相空間中,系統演化的動力學行為才能由重構空間中點的演化軌跡無奇異的表達出來。這里存在一個相空間重構維數的確定問題,即軌跡矩陣H的維數L×K的確定。徐鋒等[13]通過反復試驗的方法近似給出了相應確定原則而并未從理論上給予相應的證明，本文通過理論分析驗證該原則的正確性。

(5)

定理2.1 對于式(1)所示Hankel矩陣H，矩陣的跡可以表示為

(6)

證明依據式(2) Hankel矩陣H的定義可以得到

(7)

上式可變換為

(8)

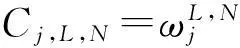
(9)

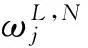
(10)

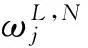
(11)

上式表明：

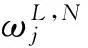
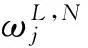
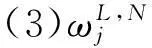
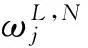
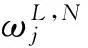
(12)

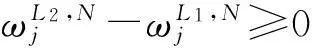
L=[(N+1)/2]

(13)

K=N-L+1

(14)

其中符號[]表示取整。

2.2最小嵌入維數確定

對于含有噪聲的離散時間序列,經由奇異值分解后得到反映真實信號的信號子空間和反映噪聲信號的噪聲子空間,這里就存在兩個子空間維數的確定問題。反映到實際運算過程中就是有效奇異值階數選擇問題。原則上,奇異值分解的濾波效果主要取決于有效奇異值的選擇。當所選的奇異值數目較少,濾波階次較低時,會導致濾波信號包含的信息不完整,甚至發生波形畸變現象,難以對原信號的有效信息特征做出準確反映;而當所選奇異值數目較多,濾波階次較高時,在濾波后的信號中仍然保留了一部分噪聲信息,無法達到信號濾波的目的。事實上,由式(4)可知,軌跡矩陣H作SVD分解后,所得到的奇異值矩陣具有如下形式：

(15)

其中Σs是反映真實信號信息的奇異值部分,而Σω則代表噪聲信息的奇異值部分,即軌跡矩陣H作SVD分解后會分為反映真實信號信息的Σs部分以及代表噪聲信息的Σω部分。由于真實信號信息和噪聲信息之間存在差異性,反映到奇異值矩陣上在交接部分奇異值大小必然會存在突變,那么在Σω和Σs過渡處的奇異值在數值上會明顯有一個突變點,也就是說突變點前的奇異值所對應的分量為真實信號信息,突變點后的奇異值所對應的分量為噪聲信息。這里通過定義奇異值差分譜來衡量相鄰奇異值的變化情況,即

(16)

其中：σi和σi+1表示相鄰兩奇異值數值大小,趙學智等[14-15]在對機械信號處理時采用了最大差分譜理論,即差分譜最大峰值處即為有效奇異值選擇點。數值仿真表明,在外部干擾和實際信號差異性不大的情況下最大差分譜理論有較好的效果,但對于實際超聲速飛行環境下的飛行器而言,其外部環境更為復雜,最大差分譜理論并不適用,這一點在后文中可見。為此,本文提出了優選差分譜峰值方法,即逐次找出奇異值差分譜上各個峰值點并分別進行信號重構,通過對比分析來尋找最優的重構曲線。

3濾波后信號的重構

最小嵌入維數即有效奇異值個數選定以后,下一步就是依據有效奇異值的個數來對濾波信號進行重構，當選定的有效奇異值個數為k時有

(17)

需要注意的是,H′并不具有Hankel矩陣的形式,它只是當選定矩陣秩為k時的一種最佳逼近,為了得到真實的信號序列sk,需要對矩陣H′中的反對角元素取平均,即

(18)

其中：p=max(1,i-K+1)，q=min(L,i)。

4數值仿真

為說明奇異譜分解的濾波效果以及驗證重構相空間維數和最小嵌入維數的選擇原則,構造信號

x(t)=sin(48πt)+sin(100πt)

(19)

在此基礎上疊加符合正態分布N(0,1)的高斯白噪聲n(t),噪聲強度D=2。疊加噪聲后信號可以表示為

y(t)=x(t)+n(t)=

sin(48πt)+sin(100πt)+n(t)

(20)

采樣頻率fs=1 000 Hz,采樣點數1 024,原始信號和疊加噪聲后信號見圖1所示。

圖1　原始信號與疊加噪聲后信號 Fig.1 Original signal and noisy signal

圖1(a)所示是加噪前的信號時域信息,圖1(b)是加噪后的信號時域信息,可以看到加噪后信號波形無論在幅值還是形狀上都變得雜亂無章，信號信息徹底淹沒在噪聲環境下。圖1(c)和圖1(d)分別表示加噪前、后的頻域信息,同樣可以看到加噪后頻域部分會出現其他峰值。下面利用奇異譜分解技術對加噪信號進行處理,采樣點數1 024,即N=1 024,由式(14)和式(15)有L=[(N+1)/2]=512，K=N-L+1=513,即相空間重構后軌跡矩陣H的維數為513×512,以此軌跡矩陣進行奇異值分解,得到的前21個奇異值見表1,相應的奇異值差分譜值如圖2所示,從圖2中可以看出奇異值峰值主要集中于前面部分,在i處于2,4,6,8,16,20和48時奇異值大小發生突變，且在i=4處出現最大峰值,δmax=122。利用式(17)和式(18)取前4個奇異值進行信號重構,重構結果如圖3所示,可以看到時域方面兩者基本吻合,重構效果明顯,經過奇異值分解重構后信號的兩個主要頻率成分f1=24 Hz及f2=50 Hz得到很好地體現。可見奇異譜分解技術在信號濾波方面是切實可行的,同時奇異值差分譜值這一指標也能較準確反映有效奇異值的個數。

表1　前21個奇異值數值情況

圖2　奇異值差分譜曲線 Fig.2 Singular value difference spectrum curve

圖3　前4個奇異值分量重構結果 Fig.3 The first four singular value components reconstruction results

5奇異譜分解在超聲速飛行器聲振試驗數據處理中的應用

通過聲振試驗對某超聲速無人機的飛行狀態進行描述，試驗模型用彈性繩吊裝于高聲強混響室，如圖4(a)所示，試驗總聲壓級共五個狀態，分別是總聲壓級140 dB、145 dB、150 dB、155 dB、160 dB，每個狀態持續30 s，在飛行器表面，安裝16個單軸向加速度傳感器，加速度測點布局如圖4(b)所示,加速度采樣頻率為64 kHz。不失一般性,本文取總聲壓級160 dB的測試數據進行分析,由于每個通道采集數據量較大,這里取其中的10 240個數據點進行分析,得到試驗后測得的總聲壓級為160 dB時測點2的時頻域信息如圖5所示。

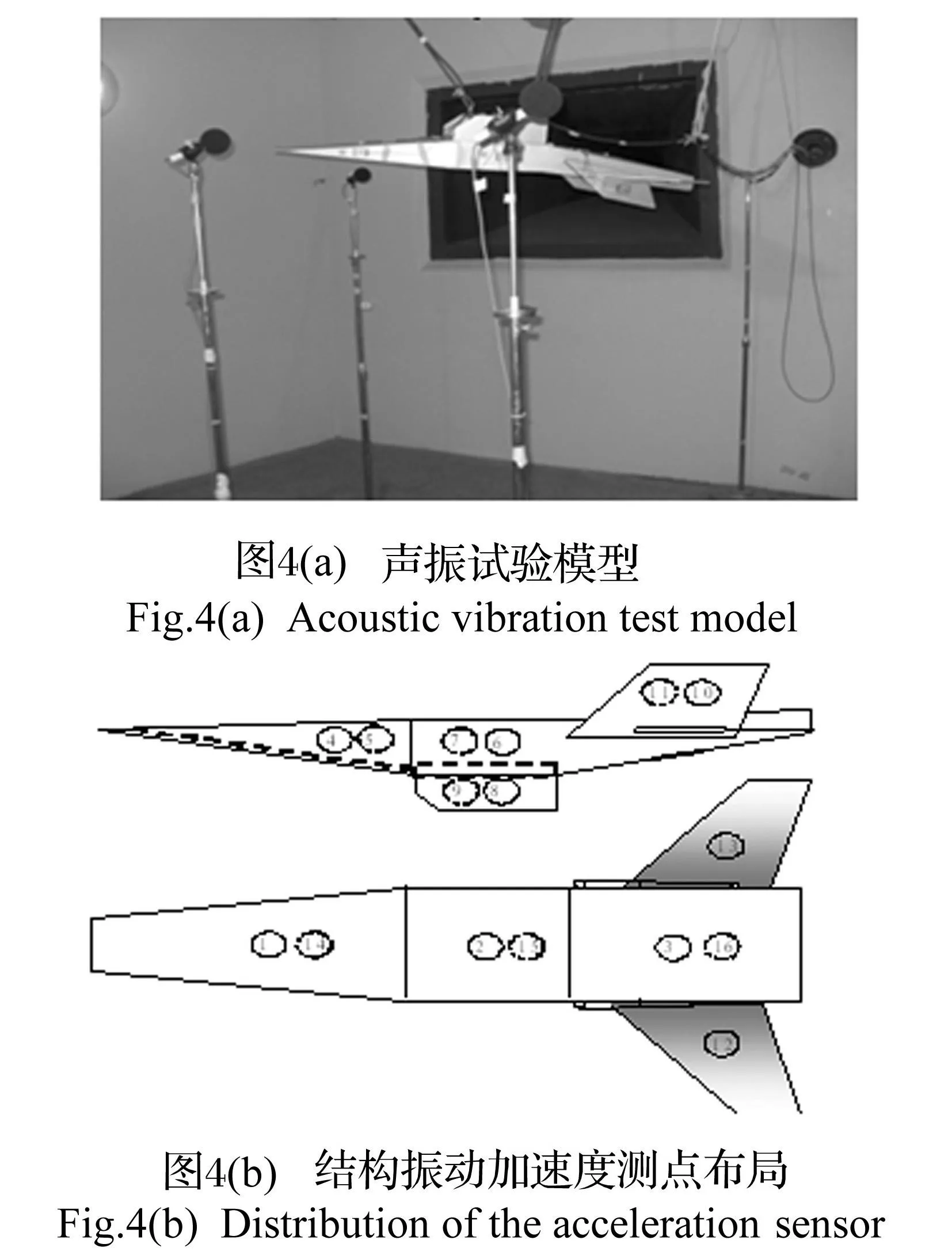
圖5　加速度測點2#時、頻域信息 Fig.5 Time domain and frequency domain of the acceleration data about sensor 2

下面利用奇異譜分解技術對實驗數據進行處理。采樣點數10 240,N=10 240,由式(14)和式(15)有L=[(N+1)/2]=4 096,K=N-L+1=4 097,即相空間重構后軌跡矩陣H的維數為4097×4096,以此軌跡矩陣進行奇異值分解,得到的前27個奇異值見表2,對應的奇異值差分譜曲線如圖6所示。

表2　前27個奇異值數值情況

圖6　奇異值差分譜曲線 Fig.6 Singular value difference spectrum curve

可以看到奇異值序列在i處于2,4,6,12,14,20,22時產生突變,且在i=2處出現最大峰值,奇異值差分譜最大值δmax=29 195,取前2個奇異值進行信號重構,重構信息如圖7所示。

圖7　前2個奇異值分量重構結果 Fig.7 The first 2 singular value component reconstruction results

圖7表示的是重構后時、頻域信息,可以看到在頻域圖中僅在218.01Hz處存在一個頻率峰值,而噪聲致振環境下結構的響應具有多頻的特性[16]。這說明僅按照最大差分譜理論難以對超聲速環境下飛行器聲振響應進行準確描述。奇異譜分解的核心思想在于真實信號和噪聲信號的分離,由于信號和噪聲的差異性此種分離在臨界處必然伴隨著突變,奇異值突變處正是這種差異性的潛在體現。盡管高速飛行器所處振動環境復雜，聲振信號存在多頻的特性，但信號和噪聲之間的差異性仍然存在。因此,這里同時考慮其它奇異值突變處的重構情況,重構結果見圖8(a)～8(f)。

圖8　重構結果 Fig.8 Reconstruction results

對比圖1及圖8(1)-8(6)可以看到,當取22個奇異值進行重構時效果最為顯著,響應信號的主要頻率成分見表3所示。

表3　聲振信號主要頻率成分

為了定量比較最大差分譜峰值理論和優選差分譜峰值理論，這里引入信噪比指標

(21)

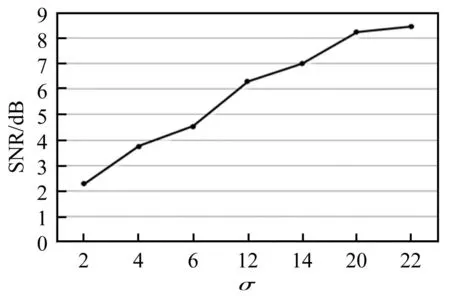
圖9　不同奇異值重構信噪比值 Fig.9 Signal to noise ratio under different singular value decomposition

可以看到按照最大差分譜理論σ=2時重構后信噪比SNR為2.30 dB,在所有峰值處奇異值重構結果中最小,當按照最優差分譜峰值理論選定有效奇異值σ=22時重構效果最為顯著,信噪比SNR達到8.49 dB。

6結論

本文利用SVD和相空間重構實現了對于高速飛行器聲振響應的狀態描述,從理論上分析了相空間重構維數及有效奇異值階數等指標并給出了相應的表達式及判定方法,為實際應用的參數選擇提供了依據,并通過仿真分析和試驗結果論證驗證了該方法的可行性，結論如下：

(1)針對以往依據經驗選擇相空間重構維數的方法從理論上進行了分析論證，分析結果表明Hankel矩陣維數接近方陣時效果最佳；

(2)奇異譜分解以信號和噪聲的差異性作為分界條件,通過尋找最優奇異譜峰值點可以確定有效奇異值個數；

(3)最大峰值理論并不適用于高速飛行器聲振響應信號的信號重構，依據本文提出的優選差分譜峰值理論進行重構維數的選擇效果較好,采用前者重構后所得信噪比僅為2.30 dB，而采用后者重構后信噪比能達到8.49 dB。

參考文獻

[1]Zhang Y M, Dai G Z, Zhang H C, et al. A SVD-based extended Kalman filter and applications to aircraft flight state and parameter estimation[C]. Proceedings of 1994 American Control Conference, Maryland: Baltimore, 1994: 1809-1813.

[2]張友民, 焦凌云, 陳洪亮,等. 基于奇異值分解的固定區間平滑新方法[J]. 控制理論與應用, 1997, 14(4): 579-583.

ZHANG You-min, JIAO Lin-yun,CHEN Hong-liang, et al. A new fixed-interval smoothing algorithm based on singular value decomposition[J]. Control Theory and Applications, 1997,14(4): 579-583.

[3]宮曉琳, 房建成. 基于SVD的R-T-S最優平滑在機載SAR運動補償POS系統中的應用[J]. 航空學報, 2009,30(2): 311-318.

GONG Xiao-lin, FANG Jian-cheng. Application of SVD-based R-T-S optimal smoothing algorithm to POS for airborne SAR motion compensation[J]. Acta Aeronoutica et Astronautica Sinica, 2009, 30(2):311-318.

[4]Shim Duk-sun, Yang Cheol-kwan. Geometric FDI based on SVD for redundant inertial sensor systems[J]. 2004 5th Asian Control Conference, 2004, 6:1094-1100.

[5]賈鵬, 張洪鉞. 基于奇異值分解的冗余慣導系統故障診斷[J]. 宇航學報, 2006, 27(5): 1076-1080.

JIA Peng, ZHANG Hong-yue. Fault detection for redundant inertial navigation system based on SVD method[J]. Journal of Astronautics, 2006, 27(5):1076-1080.

[6]Shnayderman A, Gusev A, Eskicioglu A M. A SVD based grayscale image quality measure for local and global assessment [J]. IEEE Transactions on Image Process, 2005, 14 (2): 422-429.

[7]朱衛綱, 周萌清, 徐華平,等. 基于奇異值分解的遙感圖像融合性能評估[J]. 北京航空航天大學學報，2008, 34(12): 1448-1451.

ZHU Wei-gnag, ZHOU Meng-qin, XU Hua-ping,et al. Remote sensing image fusion assessment based onSVD[J]. Journal of Beijing University of Aeronautics and Astronautic, 2008，34(12): 1448-1451.

[8]何田, 劉獻棟, 李其漢. 噪聲背景下檢測突變信息的奇異值分解技術[J]. 振動工程學報, 2006, 19(3): 399-403.

HE Tian, LIU Xian-dong, LI Qi-han. An improved method of detecting abrupt information based on singularity value decomposition in noisebackground[J]. Journal of Vibration Engineering, 2006, 19(3): 399-403.

[9]何田, 劉獻棟, 李其漢. 一種改進的航空發動機轉靜件碰摩故障診斷方法[J]. 航空動力學報, 2008, 23(6): 1093-1097.

HE Tian, LIU Xian-dong, LI Qi-han. Improved fault diagnosis method for aero engine rotor-sator rub[J]. Journal of Aerospace Power, 2008, 23(6): 1093-1097.

[10]何田, 劉獻棟, 陳亞農,等. 基于奇異值差的轉靜件碰摩故障診斷方法研究[J]. 航空動力學報, 2009, 24(10): 2296-2301.

HE Tian, LIU Xian-dong, CHEN Ya-nong,et al. Method for diagnosing rub fault of rotor-stator base on differences of singularlyvalue[J]. Journal of Aerospace Power, 2009, 24(10)：2296-2301.

[11]李月, 楊寶俊. 混沌振子系統(L-Y)與檢測[M]. 北京:科學出版社, 2007:12.

[12]Shin K, Hammond J K, White P R. Iterative SVD method for noise reduction of low-dimensional chaotic time series[J]. Mechanical Systems and Signal Processing, 1999,13(1): 115-124.

[13]徐鋒, 劉云飛. 基于中值濾波-奇異值分解的膠合板拉伸聲發射信號降噪方法研究[J]. 振動與沖擊, 2011, 30(12): 135-140.

XU Feng, LIU Yun-fei. Noise reduction of acoustic emission signal in aplaywood based on median filtering-singular value decomposition[J]. Journal of Vibration and Shock, 2011, 30(12):135-140.

[14]趙學智, 向可, 葉邦彥,等. 基于二次樣條小波細節信號峰值的有效奇異值確定[J]. 振動與沖擊，2010, 29(11): 6-12.

ZHAO Xue-zhi, XIANG Ke, YE Bang-yan , et al. Determination of effective singular values based on detailed signal peak with quadratic spline wavelet [J]. Journal of Vibration and Shock, 2010, 29(11): 6-12.

[15]趙學智, 葉邦彥. 奇異值差分譜理論及其在車床主軸箱故障診斷中的應用[J]. 機械工程學報, 2010, 46(1):100-108.

ZHAO Xue-zhi, YE Bang-yan. Processing of milling force signal and isolation of state information of milling machine based on singular valuedecomposition[J]. Chinese Journal of Mechanical Engineering,2007, 43(06): 169-174.

[16]Shorter P J, Langley R S. Vibro-acoustic analysis of complex systems[J].Journal of Sound and Vibration, 2005, 288:669-699.