軸對稱動力學問題的無網格自然鄰接點Petrov-Galerkin法

第一作者陳莘莘男，博士，副教授，1975年生

軸對稱動力學問題的無網格自然鄰接點Petrov-Galerkin法

陳莘莘,李慶華,劉永勝

(華東交通大學土木建筑學院，南昌330013)

摘要：基于無網格自然鄰接點Petrov-Galerkin法，提出了復雜軸對稱動力學問題求解的一條新途徑。幾何形狀和邊界條件的軸對稱特點，將原來的空間問題轉化為平面問題求解。計算時僅僅需要橫截面上離散節點的信息，無論積分還是插值都不需要網格。自然鄰接點插值構造的試函數具有Kronecker delta函數性質，因此能夠直接準確地施加本質邊界條件。有限元三節點三角形單元的形函數作為權函數，可以減少域積分中被積函數的階次，提高計算效率。數值算例結果表明，所提出的方法對求解軸對稱動力學問題是行之有效的。

關鍵詞：軸對稱；無網格法；動力響應；自然鄰接點插值

基金項目：國家自然科學基金資助項目(11002054, 51074076)

收稿日期：2013-11-08修改稿收到日期：2014-02-26

中圖分類號:O241; O343文獻標志碼：A

Meshless natural neighbour Petrov-Galerkin method for axisymmetric dynamic problems

CHENShen-shen,LIQing-hua,LIUYong-sheng(School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang 330013, China)

Abstract:A novel algorithm for solving complex axisymmetric dynamic problems was put forward on the basis of the meshless natural neighbour Petrov-Galerkin method. Due to axial symmetry of geometry and boundary conditions, an original three-dimensional (3D) problem was reduced into a two-dimensional (2D) problem. Only a set of discrete nodes on a cross section were needed and no meshes were required for either interpolation or integration. The natural neighbour interpolation shape functions had a Kronecker delta property and therefore the essential boundary conditions could be directly imposed. The three-node triangular finite element shape functions were taken as test functions, they reduced the orders of integrands involved in domain integrals and improved the computational efficiency. Numerical examples showed that the proposed method for solving axisymmetric dynamic problems is effective.

Key words:axisymmetric; meshless method; dynamic response; natural neighbour interpolation

作為一種新的數值計算方法，無網格法可以減少或消除網格劃分給數值計算帶來的困難，尤其在自適應分析、大變形和裂紋擴展等問題中體現出其獨特的優越性，具有廣闊的應用前景[1-4]。現有的無網格方法中，Atluri等[5]提出的無網格局部Petrov-Galerkin(MLPG)方法允許試函數和權函數選自不同的函數空間，所有積分都在基于節點的局部子域上進行，無需借助背景積分網格，被譽為是一種真正的無網格方法。但是以移動最小二乘近似為理論基礎的MLPG方法，形函數不滿足Kronecker delta函數性質，難以準確施加本質邊界條件。近年來提出的無網格自然鄰接點Petrov-Galerkin法[6-8]不僅充分發揮了局部Petrov-Galerkin法的優勢，而且采用了自然鄰接點插值構造試函數，從而可以直接準確地施加本質邊界條件。目前，該方法在很多領域都得到了廣泛的應用[9-12]。

在結構分析中常會遇到一些軸對稱問題，它們的幾何形狀、約束條件及作用的荷載都對稱于某一固定軸。軸對稱問題是彈性空間問題的一個特殊問題，利用軸對稱特性，可以將三維空間問題轉換為二維問題，從而快速有效地求解。近年來，許多學者[13-15]都致力于無網格法求解復雜軸對稱問題的研究，并相繼取得了一些進展。本文對無網格自然鄰接點Petrov-Galerkin法應用于軸對稱動力學問題進行了研究，詳細推導了離散方程，并編制了相應的計算程序。最后，通過數值算例驗證了本文方法的有效性和合理性。

1軸對稱動力學問題的控制方程

在分析軸對稱問題時，通常采用圓柱坐標系(r,θ,z)。以z軸為對稱軸，所有位移、應變和應力都與θ方向無關，只是r和z的函數。任一點的位移只有兩個方向的分量，即沿r方向的徑向位移ur和沿z方向的軸向位移uz。軸對稱動力學問題的基本方程如下：

(1)平衡方程

(1)

(2)

式中:σr,σθ,σz和τrz表示應力向量分量，br和bz表示體力向量分量，ρ是質量密度，c是阻尼系數。

(2)幾何方程

(3)

(3)本構方程

(4)

式中:

(5)

其中:E為彈性模量，v為泊松比。

應力和位移滿足如下的邊界條件

(6a)

(6b)

和初始條件

(7a)

(7b)

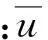
2軸對稱動力學問題的離散方程

2.1自然鄰接點插值[6-12]

TI={x∈R2:d(x,xI)<

d(x,xJ),?J≠I}

(8)

式中:d(x,xI)為點x與結點xI的距離。可見，每個TI表示的實際上是以點xI為最近離散節點的空間點位置的集合。在此基礎上，進一步可建立計算點x的二階Voronoi結構，如圖1所示。

圖1　點x的一階和二階Voronoi結構 Fig.1 First-order and second-order Voronoi cells about x

計算點x對節點xI的形函數φI(x)定義為點x與節點xI的Voronoi結構重疊區域的面積AI(x)與點x的Voronoi結構的總面積之比，即

φI(x)=AI(x)/A(x)

(9)

以圖1為例，節點1的插值形函數φ1(x)可表示為

φ1(x)=Aabfe/Aabcd

(10)

定義了各節點的插值函數后，點x的位移函數可以寫為

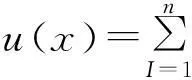
(11)

式中:uI(I=1,2,…,n)是點x周圍n個自然鄰接點的節點位移向量，φI(x)為對應節點的形函數。

2.2控制方程的弱形式及其離散化

(12)

(13)

式中:vI為加權函數。

對方程(12)的左邊項進行分部積分并利用散度定理后，可得

(14)

(15)

圖2　局部多邊形子域 Fig.2 The local polygonal sub-domains

(16)

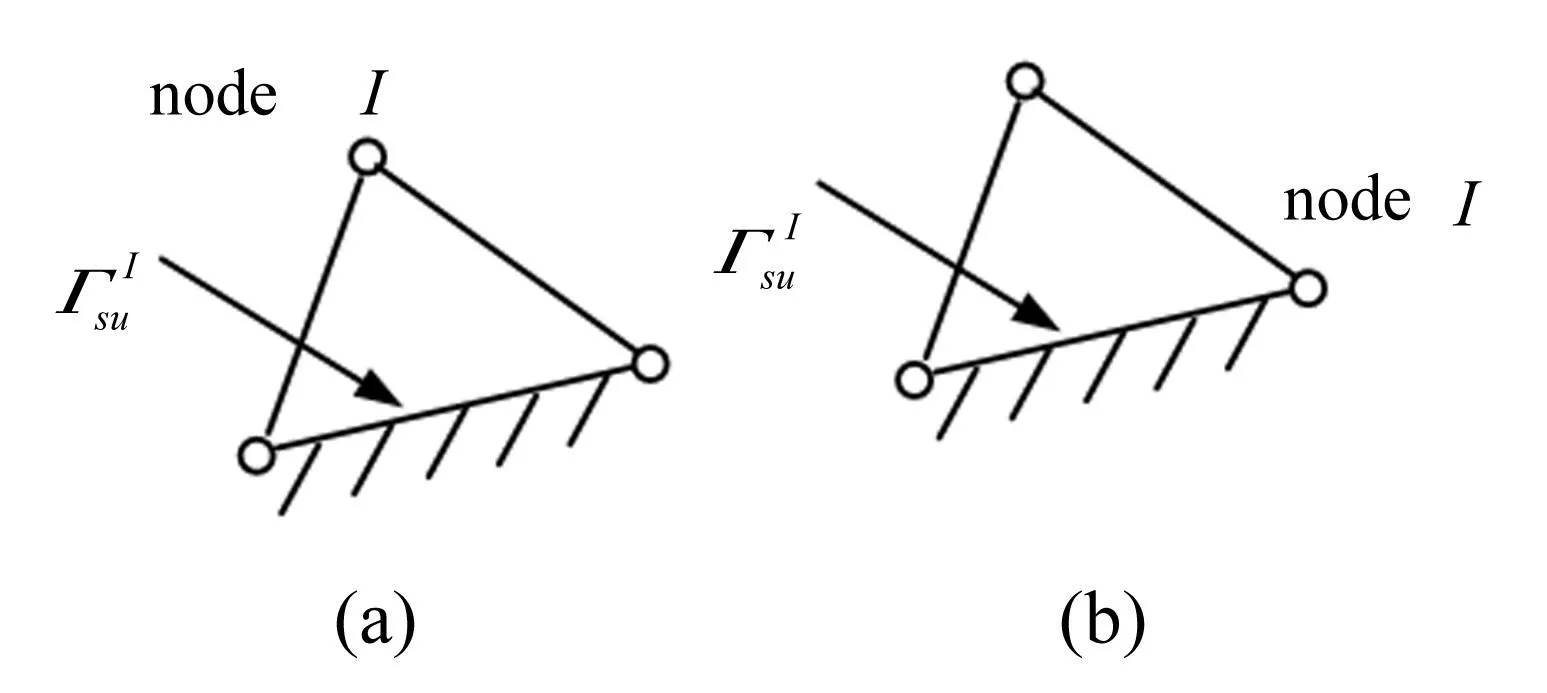
圖3　子域Ω I s上的位移邊界Γ I su Fig.3 Essential boundary condition Ω I s over sub-domain Γ I su

將式(16)代人式(14),并注意到vI=NI，有

(17)

同理，由方程(13)可得

(18)

聯立方程(17)和方程(18)，可得

(19)

式中:

u={ur,uz}T,σ={σr,σθ,σz,τrz}T

(20a)

b={br,bz}T,t={tr,tz}T

(20b)

(20c)

由于只對空間域進行離散，求解域Ω內的試函數u(x,t)可由式(11)表示為

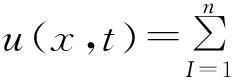
(21)

將空間離散后的位移表達式(21)代入式(19),可得到系統的運動方程如下：

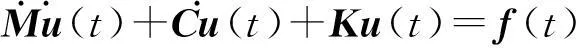
(22)

式中:M,C,K和f(t)分別是系統的質量矩陣、阻尼矩陣、剛度矩陣和節點載荷向量，且它們各元素可具體表示為：

(23a)

(23b)

(23c)

(23d)

其中，

(24a)

(24b)

采用Newmark法對方程(22)進行積分即可以求得系統的動態響應。

圖4　受內壓的厚壁圓筒 Fig.4 A thick-walled cylinder subjected to internal pressure

3數值算例

3.1受突加載荷的厚壁圓筒

有一無限長厚壁圓筒，其內半徑a=0.1 m,外半徑b=0.2 m，受突加內壓力p=75 MPa的作用，如圖4所示。材料的彈性模量E=2.1×1011Pa，泊松比v=0.3，質量密度ρ=7.85×103kg/m3。

計算分析中，截取長L=0.1 m的厚壁圓筒作為計算結構，節點布置方案見圖5，且z=0和z=L的節點施加軸向零位移約束。采用時間步長Δt=4.0×10-7s計算得到了不計阻尼情況下內表面的徑向位移隨時間的變化曲線，如圖6所示。為了進行對比，圖6還給出了有限元軟件ABAQUS(采用6400個CAX4R單元)的計算結果。從圖6可以看出，本文的計算結果與ABAQUS的計算結果都吻合很好，從而表明了本文方法的有效性。

圖5　厚壁圓筒節點布置 Fig.5 Nodal distribution for a thick-walled cylinder

圖6　厚壁圓筒內表面的徑向位移 Fig.6 Radial displacement history at the inner surface of the thick-walled cylinder

3.2受突加載荷的厚壁球殼

有一厚壁球殼，其外壁半徑R1=0.2 m，內壁半徑R2=0.16 m，受突加內壓力p=75 MPa的作用。材料參數為E=2.1×1011Pa，v=0.3，ρ=7.85×103kg/m3。

由于對稱性，采用如圖7所示的節點布置方案。計算時時間步長取為Δt=3.0×10-7s。為了檢驗方法的有效性，本文采用有限元軟件ABAQUS使用12000個CAX4R單元得出的解來對比。圖8給出了不計阻尼情況下圓球內壁的徑向位移隨時間的變化曲線，從圖上可以看出本文方法和ABAQUS的結果非常吻合，從而進一步說明了本文方法的有效性。

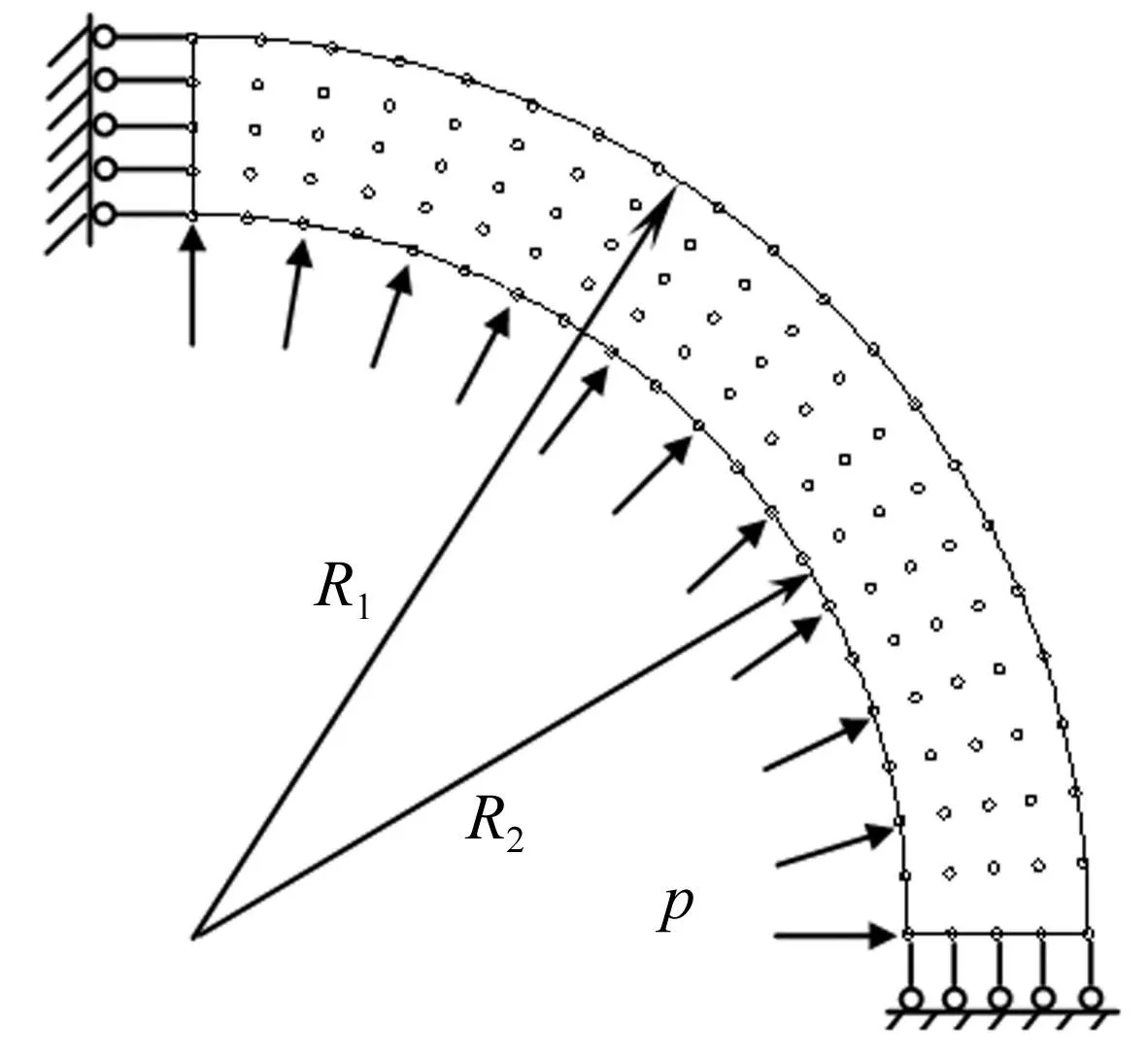
圖7　厚壁球殼節點布置 Fig.7 Nodal distribution for a thick-walled spherical shell

圖8　厚壁球殼內表面的徑向位移 Fig.8 Radial displacement history at the inner surface of the thick-walled spherical shell

4結論

無網格自然鄰接點Petrov-Galerkin法只需要用到模型分布在域內和邊界上的節點，并不需要任何單元和網格，因此是一種真正的無網格方法。在求解過程中，采用有限元三節點三角形單元的形函數作為權函數，減少了域積分中被積函數的階次，提高了計算效率。基于自然鄰接點插值構造的試函數，具有Kronecker delta函數性質，從而可以直接準確地施加本質邊界條件。

本文借助無網格自然鄰接點Petrov-Galerkin法的基本原理，詳細推導了軸對稱動力學問題的計算公式，并編制了相應的計算程序，最后通過數值算例論證了本文方法的有效性。本文方法還可容易地推廣到軸對稱裂紋問題的求解計算。

參考文獻

[1]Belytschko T, Krongauz Y. Meshless methods: An overview and recent developments [J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139(9): 3-47.

[2]劉欣. 無網格方法[M]. 北京：科學出版社，2011.

[3]張雄，劉巖，馬上. 無網格法的理論及應用[J]. 力學進展, 2009, 39(1): 1-36.

ZHANG Xiong, LIU Yan, MA Shang. Meshfree methods and their applications [J]. Advances in Mechanics, 2009, 48(5): 1-36.

[4]王峰，林皋，鄭保敬，等.基于滑動Kriging插值的無網格MLPG法求解結構動力問題[J]. 振動與沖擊, 2014,33(4): 27-31.

WANG Feng, LIN Gao, ZHENG Bao-jing, et al. MLPG method based on moving Kriging interpolation for structural dynamic analysis[J].Journal of Vibration and Shock, 2014,33(4): 27-31.

[5]Atluri S N, Zhu T. A new meshless local Petrov-Galerkin (MLPG) approach in computational mechanics [J]. Computational Mechanics, 1998, 22: 117-127.

[6]蔡永昌，朱合華，王建華. 基于Voronoi結構的無網格局部Petrov-Galerkin方法[J]. 力學學報, 2002, 35(2): 187-193.

CAI Yong-chang, ZHU He-hua, WANG Jian-hua. The meshless local Petrov-Galerkin method based on the Voronoi cells [J]. Acta Mechanica Sinica, 2003, 35(2): 187-193.

[7]Cai Y C, Zhu H H. A meshless local natural neighbour interpolation method for stress analysis of solids [J]. Engineering Analysis with Boundary Elements, 2004, 28: 607-613.

[8]Wang K, Zhou S J, Shan G J. The natural neighbour Petrov-Galerkin method for elasto-statics [J]. International Journal for Numerical Methods in Engineering, 2005, 63: 1126-1145.

[9]李順利，龍述堯，李光耀. 自然鄰接點局部Petrov-Galerkin法求解中厚板彎曲問題[J]. 湖南大學學報, 2011, 38(1): 53-57.

LI Shun-li, LONG Shu-yao, LI Guang-yao. Natural neighbour Petrov-Galerkin method for moderately thick plates [J]. Journal of Hunan University, 2011, 38(1): 53-57.

[10]陳莘莘，劉應華，岑章志. 彈塑性結構安定下限分析的無網格局部Petrov-Galerkin法[J]. 力學學報, 2009, 41(5): 713-721.

CHEN Shen-shen, LIU Ying-hua, CEN Zhang-zhi. A meshless local Petrov-Galerkin method for static shakedown analysis of elasto-plastic structures [J]. Acta Mechanica Sinica, 2009, 41(5): 713-721.

[11]Chen S S, Li Q H, Liu Y H, et al. Dynamic elastoplastic analysis using the meshless local natural neighbour interpolation method [J]. International Journal of Computational Methods, 2011, 8(3): 463-481.

[12]王凱，周慎杰，聶志峰，等. 基于局部自然鄰近無網格法的形狀優化[J]. 機械工程學報, 2009, 45(10): 185-191.

WANG Kai, ZHOU Shen-jie, NIE Zhi-feng, et al. Shape optimization based on the local natural neighbour Petrov-Galerkin method[J]. Journal of Mechanical Engineering, 2009, 45(10): 185-191.

[13]何沛祥，李子然，吳長春. 軸對稱問題中的無網格Galerkin法[J]. 中國科學技術大學學報, 2003, 33(3): 318-323.

HE Pei-xiang,LI Zi-ran, WU Chang-chun. Element free Galerkin method for axisymmetric solids[J]. Journal of University of Science and Technology of China, 2003, 33(3): 318-323.

[14]陳建橋，梁元博，丁亮. 無網格局部Petrov-Galerkin法求解軸對稱問題[J]. 華中科技大學學報, 2007, 24(4): 9-12.

CHEN Jian-qiao, LIANG Yuan-bo, DING Liang. Numerical analysis of axisymmetric problems by MLPG [J]. Journal of Huazhong University of Science and Technology, 2007, 24(4): 9-12.

[15]楊建軍，鄭建龍. 無網格MLPG法求解軸對稱彈性力學問題[J]. 工程力學, 2012, 29(8): 8-13.

YANG Jian-jun, ZHENG Jian-long. Analysis of axisymmetric elasticity problems using the meshless local Petrov-Galerkin method [J]. Engineering Mechanics, 2012, 29(8): 8-13.