基于數(shù)字序列編碼遺傳算法的高層結(jié)構(gòu)黏滯阻尼器優(yōu)化布置

2015-12-30 03:43:17燕樂緯,陳洋洋,周云

振動(dòng)與沖擊 2015年3期

第一作者燕樂緯男，博士，講師，1978年10月生

通信作者周云男，教授，博士生導(dǎo)師，1965年9月生

燕樂緯1, 陳洋洋2，周云1

(1.廣州大學(xué)土木工程學(xué)院，廣州510006; 2. 廣州大學(xué)工程抗震研究中心，廣州510006)

摘要：提出一種基于數(shù)字序列編碼遺傳算法的高層結(jié)構(gòu)黏滯阻尼器優(yōu)化布置方法，解決了允許各層阻尼器安裝數(shù)量不同時(shí)，二進(jìn)制編碼的標(biāo)準(zhǔn)遺傳算法不能完備表達(dá)求解空間的問題。數(shù)字序列編碼用染色體的一個(gè)基因位表示一個(gè)阻尼器的安裝位置，其數(shù)值表示該阻尼器的安裝層數(shù)。在這一編碼方案下，優(yōu)化問題基因型空間中的染色體和表現(xiàn)型空間中的可選布置方案一一對(duì)應(yīng)，編碼滿足嚴(yán)格的合法性、完備性、Lamarckian性質(zhì)以及強(qiáng)因果性。與數(shù)字序列編碼方式相對(duì)應(yīng)，離散重組交叉算子保證了種群的有效進(jìn)化。此外，基于染色體目標(biāo)函數(shù)值的相對(duì)大小構(gòu)造適應(yīng)度函數(shù)，能夠充分體現(xiàn)種群中染色體的適應(yīng)度差異，加速種群的進(jìn)化，進(jìn)而獲得優(yōu)化問題的全局最優(yōu)解。對(duì)多遇地震下20層Benchmark結(jié)構(gòu)的阻尼器布置方案進(jìn)行了優(yōu)化，計(jì)算結(jié)果表明了該方法的有效性。

關(guān)鍵詞：數(shù)字序列編碼；遺傳算法；相對(duì)適應(yīng)度；阻尼器；高層結(jié)構(gòu)

收稿日期：2014-05-07修改稿收到日期：2014-09-25

中圖分類號(hào):O224；TU311文獻(xiàn)標(biāo)志碼：A

Optimal positioning of viscous dampers in tall buildings based on digital sequence conding genetic algorithm

YANLe-wei1,CHENYang-yang2,ZHOUYun1(1. School of Civil Engineering, Guangzhou University, Guangzhou 510006, China; 2. Earthquake Engineering Research and Test Center, Guangzhou University, Guangzhou 510006, China)

Abstract:An optimal locating method of viscous dampers in tall buildings was presented based on digital sequence coding genetic algorithm (DSCGA). Compared with standard genetic algorithm (SGA), the presented algorithm could completely represent the solution space of the optimization problem when the number of dampers was not equal in each damper-installation storey. A gene bit of digital sequence code represented an installation position of a damper, its value denoted the damper-installation storey. With the presented digital sequence coding, the size of the genotype space was exactly consistent with that of the phenotype space, while strict legitimacy, completeness, Lamarckian property, and strong causality were satisfied. The discrete-recombination cross operator, corresponding to the digital sequence coding, ensured the effective evolution of the population. Furthermore, a fitness function was constructed based on a relative objective function value, it could not only fully embody the fitness difference in population but also promote effective evolution to obtain the global optimal solution as a result. The method was applied for a typical damper positioning optimization problem, a 20-storey Benchmark structure under a frequent seismic level was considered. The efficiency and applicability of the presented algorithm were assessed.

Key words:digital sequence coding; genetic algorithm; relative fitness; damper; tall buildings

黏滯阻尼器(Viscous Damper)是一種廣泛應(yīng)用于高層、超高層建筑結(jié)構(gòu)的被動(dòng)減震控制裝置。用遺傳算法對(duì)高層結(jié)構(gòu)的黏滯阻尼器安裝位置進(jìn)行優(yōu)化以提高耗能效率、降低消能減震系統(tǒng)的成本，是當(dāng)前研究的一個(gè)熱點(diǎn)。對(duì)于選定安裝阻尼器的樓層安裝相同數(shù)量阻尼器的優(yōu)化問題，可以采用二進(jìn)制編碼的標(biāo)準(zhǔn)遺傳算法(Standard Genetic，Algorithm， SGA)進(jìn)行優(yōu)化。在此類問題中，每一個(gè)樓層只有安裝阻尼器和不安裝阻尼器兩種狀態(tài)，這兩種狀態(tài)可以用{1,0}表示，恰好對(duì)應(yīng)于遺傳算法的一個(gè)基因位。將整個(gè)高層結(jié)構(gòu)的阻尼器安裝狀態(tài)列入一個(gè)數(shù)列中，就形成了標(biāo)準(zhǔn)遺傳算法的染色體。根據(jù)結(jié)構(gòu)的響應(yīng)設(shè)置適應(yīng)度函數(shù)，對(duì)阻尼器安裝布置的參數(shù)空間進(jìn)行遺傳優(yōu)化，得到的最佳染色體就是優(yōu)化問題的最優(yōu)解，也即阻尼器的最優(yōu)布置方案[1]。

但是，實(shí)際的高層結(jié)構(gòu)阻尼器優(yōu)化配置問題中，各層的阻尼器安裝數(shù)量不一定相同[2]，用二進(jìn)制編碼的標(biāo)準(zhǔn)遺傳算法求解此類問題會(huì)遇到很大的困難甚至難以求解[3]。

針對(duì)具體的工程優(yōu)化問題，選用適當(dāng)?shù)木幋a和相應(yīng)的遺傳算子進(jìn)行優(yōu)化，是遺傳算法研究一個(gè)重要的方向[4]。Dyer等[5]將實(shí)數(shù)編碼遺傳算法應(yīng)用于航天工程中導(dǎo)彈推進(jìn)系統(tǒng)的優(yōu)化設(shè)計(jì)。Panteleev等[6]對(duì)比了二進(jìn)制編碼和實(shí)數(shù)編碼遺傳算法在次優(yōu)綜合控制問題中的優(yōu)化效果。陳瑤等[7]利用整數(shù)編碼的遺傳算法提出了兩點(diǎn)組群雜交算子和基于適應(yīng)值的組群啟發(fā)式變異算子，解決了管理工程中的分組優(yōu)化強(qiáng)NP難問題。此外，F(xiàn)ujita等[8]和李宏男等[9]分別提出了在不同的優(yōu)化目標(biāo)和評(píng)價(jià)準(zhǔn)則下對(duì)阻尼器進(jìn)行優(yōu)化配置的問題。

本文將在以往工作的基礎(chǔ)上[10-11]，設(shè)計(jì)數(shù)字序列編碼、相對(duì)適應(yīng)度函數(shù)和離散重組交叉算子，解決高層結(jié)構(gòu)各層阻尼器安裝數(shù)量不同時(shí)的優(yōu)化布置問題。

1計(jì)算模型

1.1結(jié)構(gòu)模型

阻尼器優(yōu)化配置問題的研究需要反復(fù)分析不同阻尼器配置方案下的結(jié)構(gòu)響應(yīng)，反饋給遺傳算法進(jìn)行迭代優(yōu)化。以阻尼器在各層的分布狀態(tài)為設(shè)計(jì)變量時(shí)，結(jié)構(gòu)體系的響應(yīng)可以利用層模型的動(dòng)力響應(yīng)分析得到。

一般情況下，線性黏滯阻尼器的出力取決于其瞬時(shí)相對(duì)速度的大小[12]：

(1)

地震作用下，安裝黏滯阻尼器的結(jié)構(gòu)體系的運(yùn)動(dòng)微分方程可表示如下：

(2)

1.2優(yōu)化模型

高層結(jié)構(gòu)阻尼器優(yōu)化布置問題的一般數(shù)學(xué)表達(dá)形式為：

(3)

式中：n是結(jié)構(gòu)層數(shù)，X是阻尼器的布置方案；t是動(dòng)載荷作用時(shí)間；g(X,t)≤0是經(jīng)過標(biāo)準(zhǔn)化處理的約束條件。

f是優(yōu)化問題的目標(biāo)函數(shù)。出于結(jié)構(gòu)安全性和舒適性的考慮，一般需要優(yōu)化結(jié)構(gòu)在地震動(dòng)時(shí)程內(nèi)的層間位移角峰值和加速度峰值[9]。

2數(shù)字序列編碼遺傳算法

2.1編碼

用遺傳算法求解工程中的優(yōu)化問題時(shí)，首先要考慮的就是所用編碼能否恰當(dāng)?shù)乇硎緝?yōu)化問題的求解空間，以及能否通過相應(yīng)的遺傳算子實(shí)現(xiàn)問題的優(yōu)化求解[13]。

由于二進(jìn)制編碼的基因位只有{0,1}兩種狀態(tài)，當(dāng)各層配置的阻尼器數(shù)量不相同時(shí)，不能用一個(gè)基因位表示一層的阻尼器安裝狀態(tài)。如果用多個(gè)基因位表示一層的阻尼器安裝狀態(tài)，雖然理論上可行，但隨著樓層的增加，將會(huì)使染色體編碼長度成倍增加，引發(fā)遺傳優(yōu)化過程的“維數(shù)災(zāi)難”而難于求解。

例如，文獻(xiàn)[3]用6個(gè)二進(jìn)制編碼表示一層結(jié)構(gòu)上的阻尼器數(shù)量，n層結(jié)構(gòu)的編碼長度為6n，并用此方法對(duì)一棟6層結(jié)構(gòu)進(jìn)行了阻尼器優(yōu)化配置(編碼長度36)。如果結(jié)構(gòu)層數(shù)增加到20層，則染色體編碼長度長達(dá)20×6=120，遺傳優(yōu)化過程所需的計(jì)算量和計(jì)算時(shí)間都將是難以承受的。

此外，用二進(jìn)制碼串表示高層結(jié)構(gòu)的阻尼器配置方案還存在合法性(legality)的問題。當(dāng)安裝阻尼器的總層數(shù)預(yù)先確定時(shí)，遺傳操作各步驟產(chǎn)生的染色體中1的數(shù)量是不確定的，總數(shù)與給定的阻尼器安裝層數(shù)不一定相符合。要避免此問題，就需要在交叉算子和變異算子中進(jìn)行限定，這也會(huì)浪費(fèi)大量的計(jì)算時(shí)間和計(jì)算資源。

事實(shí)上，由于樓層數(shù)和阻尼器安裝數(shù)目均為整數(shù)，用整數(shù)序列表示高層結(jié)構(gòu)阻尼器的布置狀態(tài)是最自然、最合理的方式。在總的阻尼器安裝數(shù)量確定的情況下，有兩種整數(shù)編碼方案可供選擇，即

方案A：染色體的每一項(xiàng)為一個(gè)基因位，表示一個(gè)樓層，其數(shù)值表示該層的阻尼器安裝數(shù)目。例如，序列(0 0 1 0 2 1 0 1 3 0 0 0 1 0 1 0 0 0 0 0)表示在20層結(jié)構(gòu)的第3、6、8、13、15層各布置一個(gè)阻尼器，在第5層布置2個(gè)阻尼器，在第9層布置3個(gè)阻尼器，阻尼器總數(shù)為10個(gè)。

方案B：染色體的每一項(xiàng)為一個(gè)基因位，表示一個(gè)阻尼器，其數(shù)值表示該阻尼器的安裝層數(shù)。例如，方案A中例舉的阻尼器配置方案可以表示為(3 5 5 6 8 9 9 9 13 15)。

用二進(jìn)制編碼時(shí)，也有兩種編碼方式：

方案C：僅用一個(gè)基因位表示一層的阻尼器安裝狀態(tài)。由于此方案不能表示一層安裝多個(gè)阻尼器的情況，方案A、B中的例子不能用此方案表示。

方案D：用多個(gè)基因位表示一層的阻尼器安裝狀態(tài)。由于阻尼器總數(shù)為10，每層需要用4個(gè)基因位才能表示出所有可能的情況。例如第5層布置兩個(gè)阻尼器，編碼表示為(0 0 1 0)，第9層布置3個(gè)阻尼器，編碼表示為(0 0 1 1)，全部20層的編碼總長度為4×20=80。

以上四種編碼的對(duì)比如表1所示。表中所列位串長度和基因型空間的大小均以20層結(jié)構(gòu)安裝10個(gè)阻尼器為例計(jì)算，此時(shí)所有的可行解數(shù)量，也即表現(xiàn)型空間的大小為2010。

表1　不同編碼方式的比較

從表中可以看出，方案A、C、D都會(huì)產(chǎn)生大量不合法的染色體，導(dǎo)致其不滿足Lamarckian性質(zhì)(優(yōu)良基因遺傳性質(zhì))，因果性(基因型空間的小擾動(dòng)對(duì)應(yīng)表現(xiàn)型空間的小擾動(dòng))較差。此外，方案C還不能表示各層阻尼器配置數(shù)量不同的狀態(tài)，不具備完備性。只有方案B基因型空間中的染色體和表現(xiàn)型空間的可行解一一對(duì)應(yīng)，既滿足合法性，又滿足完備性。并因此而具備很強(qiáng)的Lamarckian性質(zhì)和因果性，能夠保證遺傳優(yōu)化過程的順利實(shí)施。

在方案B中，各基因位的數(shù)值僅表示樓層序號(hào)，無數(shù)值大小意義，可以稱為數(shù)字序列編碼。數(shù)字序列編碼方案和與之對(duì)應(yīng)的遺傳算子相結(jié)合構(gòu)成的遺傳算法，稱為數(shù)字序列編碼遺傳算法(Digital Sequence Coding Genetic Algorithm，DSCGA)。

2.2離散重組交叉算子

需要指出的是，本文所提的數(shù)字序列編碼雖然在形式上與多參數(shù)整數(shù)編碼相類似，在編碼層次上卻有著本質(zhì)的區(qū)別。數(shù)字序列編碼的可變參數(shù)為阻尼器的布置方案，整個(gè)數(shù)字序列表示一種可行布置方案，序列中的每個(gè)元素表示一個(gè)阻尼器的安裝位置，處于基因?qū)哟巍６鄥?shù)整數(shù)編碼由多個(gè)獨(dú)立的參數(shù)序列組成，各元素之間沒有彼此依賴關(guān)系，屬于個(gè)體的局部組分層次，基因包含在元素?cái)?shù)值之中。這一基因?qū)哟蔚牟顒e反應(yīng)在遺傳操作過程中，最典型的體現(xiàn)就是交叉算子的不同。

交叉算子是遺傳算法中最重要的遺傳算子之一。根據(jù)遺傳算法的積木塊假設(shè)，交叉算子通過重組父代的特性來產(chǎn)生子代，屬于基因?qū)用娴倪z傳操作。由于多參數(shù)整數(shù)編碼的基因包含于序列元素的數(shù)值之中，需要采用算數(shù)交叉算子才能實(shí)現(xiàn)染色體的基因交換。而在本文所提的DSCGA中，序列中的元素本身就處于基因?qū)哟危淙≈祪H表示阻尼器安裝位置，無數(shù)值大小意義。因而對(duì)其進(jìn)行算術(shù)交叉運(yùn)算不僅毫無意義，而且會(huì)破壞算法的Lamarchkian性質(zhì)。合理的做法是交換序列中的元素，有效地地實(shí)現(xiàn)基因重組，生成具備父代優(yōu)良基因的子代個(gè)體。具體的操作步驟包括：

Step1：在父代種群中隨機(jī)選擇兩個(gè)個(gè)體，準(zhǔn)備進(jìn)行交叉操作。

Step2：生成一個(gè)在(0,1)上均勻分布的隨機(jī)數(shù)τ，用lc=ceil[τ(l-1)]確定交叉位置lc，式中l(wèi)為位串長度，ceil[]為向上取整函數(shù)；

Step3：交換父代個(gè)體交叉位置之后的位串，生成子代個(gè)體；

Step4：對(duì)生成的子代個(gè)體重新排序，使之符合順序原則。

這一交叉算子稱為離散重組交叉算子，其形式與二進(jìn)制編碼遺傳算法的單點(diǎn)交叉相類似。之所以能夠采用這種方式，是數(shù)字序列編碼的符號(hào)性而非數(shù)值性決定的。執(zhí)行離散重組交叉算子之后，子代個(gè)體可能會(huì)出現(xiàn)排序混亂問題，需要用排序命令重新排序，以便執(zhí)行下一步的遺傳操作。

例如，對(duì)兩個(gè)選定的準(zhǔn)備進(jìn)行交叉操作的個(gè)體：

父代個(gè)體X1：2 2 3 3│3 6 7 8 10 12

父代個(gè)體X2：1 2 2 4│5 7 7 8 11 16

若位串中豎線所在位置為隨機(jī)選定的交叉位置，則交叉得到的新個(gè)體為：

1 2 2 3 4 6 7 8 10 12

即完成了交叉操作。

2.3相對(duì)適應(yīng)度函數(shù)

輪盤賭選擇算子的優(yōu)點(diǎn)是能夠定量表示染色體適應(yīng)度的差異。采用輪盤賭選擇算子時(shí)，染色體的適應(yīng)度值具有絕對(duì)意義，適應(yīng)度的數(shù)值大小會(huì)直接影響被選中的概率[14]。

為了實(shí)現(xiàn)從目標(biāo)函數(shù)值到適應(yīng)度函數(shù)值的映射，一般的做法是采用界限構(gòu)造法構(gòu)造適應(yīng)度函數(shù)[15]，即

F(x)=Cmax-f(x)

(4)

為保證適應(yīng)度F(x)非負(fù)，往往需要給最大值Cmax設(shè)定較大的裕度。其結(jié)果是改變了目標(biāo)函數(shù)值的相對(duì)大小，輪盤賭選擇優(yōu)勝劣汰的選擇意義被弱化，這將會(huì)嚴(yán)重影響遺傳算法優(yōu)化的計(jì)算效率。

為解決這一問題，本文作者在文獻(xiàn)[10]中提出了一種基于目標(biāo)函數(shù)相對(duì)大小的適應(yīng)度函數(shù)構(gòu)造方法。設(shè)規(guī)模為N的種群中，第i個(gè)染色體的目標(biāo)函數(shù)值為f(xi)，則其適應(yīng)度可以按下式計(jì)算：

(5)

這樣得到的適應(yīng)度可以稱為相對(duì)適應(yīng)度(Relative fitness)。采用相對(duì)適應(yīng)度可以避免事先預(yù)估Cmax，計(jì)算得到的相對(duì)適應(yīng)度能夠最直接地體現(xiàn)種群中各個(gè)染色體目標(biāo)函數(shù)值之間的差異，使目標(biāo)函數(shù)值(層間位移角和加速度等結(jié)構(gòu)響應(yīng))小的染色體獲得較大的選擇概率，目標(biāo)函數(shù)值較大的染色體獲得較小的選擇概率，目標(biāo)函數(shù)值最大的染色體直接被剔除。

例如，某規(guī)模為100的種群，一次迭代計(jì)算得到的目標(biāo)函數(shù)最小值為2.3×10-3，最大值為2.7×10-3，平均值為2.5×10-3。表2給出了采用界限構(gòu)造法目標(biāo)函數(shù)(預(yù)設(shè)界限值Cmax=4×10-3)和相對(duì)適應(yīng)度目標(biāo)函數(shù)時(shí)，不同層次染色體的選擇概率。

表2　采用不同適應(yīng)度構(gòu)造方法時(shí)的選擇概率

從表中可以看出，采用相對(duì)適應(yīng)度方法構(gòu)造適應(yīng)度函數(shù)時(shí)，最優(yōu)染色體和最差染色體被選中的概率差距明顯大于界限構(gòu)造法。優(yōu)良染色體的存活率將會(huì)大幅提高，帶有優(yōu)良基因的模式將能以最合理的概率存活下來，而不良模式將會(huì)以很大的概率被摒棄。

2.4遺傳算法的其它問題

對(duì)應(yīng)于序列編碼，采用以較低的變異概率隨機(jī)變動(dòng)某一基因位的取值的方式實(shí)現(xiàn)染色體的變異。具體操作步驟是:①根據(jù)變異概率選定需要變異的染色體；②隨機(jī)選定一個(gè)變異位；③將變異位上的數(shù)值變異為[1,N]范圍內(nèi)的任意整數(shù)值，N為結(jié)構(gòu)層數(shù)。其在表現(xiàn)型空間的意義為：將父代給出的解所表示的某層安裝的阻尼器隨機(jī)移動(dòng)到另一層。

最優(yōu)保持策略是遺傳算法研究的重要成果之一。研究表明，采用了最優(yōu)保持策略的遺傳算法能依概率收斂到優(yōu)化問題的全局最優(yōu)解，不采用最優(yōu)保持策略的遺傳算法則不具備這一收斂性。在本文中，采用以下方式實(shí)現(xiàn)最優(yōu)保持策略：計(jì)算新一代種群的目標(biāo)函數(shù)值，若子代種群中最優(yōu)染色體的目標(biāo)函數(shù)值高于父代種群中的最優(yōu)染色體(這表示父代最優(yōu)染色體的適應(yīng)度值優(yōu)于子代最優(yōu)染色體)，則用父代種群的最優(yōu)染色體代替子代種群中的最差染色體，也即目標(biāo)函數(shù)值最大的一個(gè)。

2.5計(jì)算流程圖

在本章的最后，給出基于DSCGA高層結(jié)構(gòu)阻尼器優(yōu)化配置方法的計(jì)算流程圖示于圖1。

圖1　計(jì)算流程圖 Fig.1 Calculation flowchart

3算例

本章用序列編碼遺傳算法對(duì)多遇地震下20層Benchmark模型進(jìn)行阻尼器優(yōu)化布置，并與二進(jìn)制編碼的標(biāo)準(zhǔn)遺傳算法進(jìn)行對(duì)比，以驗(yàn)證本文所提方法的有效性。

3.120層Benchmark模型

20層Benchmark模型為鋼框架結(jié)構(gòu)。地上20層除首層層高為5.49 m外，其余各層層高均為3.96 m。各層質(zhì)量和剛度如表3所示[16]。

表3　20層Benchmark模型結(jié)構(gòu)參數(shù)

3.2優(yōu)化問題描述

要求在此20層Benchmark結(jié)構(gòu)上安裝多個(gè)等效阻尼器系數(shù)為ceq=1.05×108N·s/m的黏滯阻尼器，選擇最佳的安裝位置，優(yōu)化結(jié)構(gòu)在7度多遇地震加速度時(shí)程作用下的抗震性能。

優(yōu)化工作分兩個(gè)階段進(jìn)行。第一階段研究阻尼器數(shù)量一定(10個(gè))時(shí)，不同地震波作用下，DSCGA與SGA的優(yōu)化配置結(jié)果對(duì)比。本文選取El Centro波、DEL AMO BLVD-90波和Northbridge波(峰值55gal)，以結(jié)構(gòu)最大層間位移角和峰值加速度為優(yōu)化目標(biāo)進(jìn)行優(yōu)化。地震波的基本數(shù)據(jù)見表4。

表4　選用的3條地震波

第二階段研究研究阻尼器數(shù)量不同時(shí)，同一地震波作用下DSCGA與SGA的優(yōu)化配置結(jié)果對(duì)比。仍以結(jié)構(gòu)最大層間位移角和峰值加速度為優(yōu)化目標(biāo)進(jìn)行優(yōu)化，選取El Centro波(峰值55 gal)作為地震波時(shí)程輸入，對(duì)比阻尼器數(shù)量為8個(gè)、10個(gè)、12個(gè)時(shí)的優(yōu)化配置結(jié)果。

采用本文提出的DSCGA和帶有精英保持策略的SGA(編碼方案C)分別進(jìn)行優(yōu)化。除了編碼方式之外， DSCGA和SGA的控制參數(shù)完全相同，即種群規(guī)模N=300，最大進(jìn)化代數(shù)T=300，交叉概率pc=0.8，變異概率pm=0.2。

3.3優(yōu)化結(jié)果對(duì)比分析

采用相對(duì)適應(yīng)度時(shí)，不同代種群的適應(yīng)度計(jì)算標(biāo)準(zhǔn)不同。為觀測種群的進(jìn)化過程，可以用目標(biāo)函數(shù)值的進(jìn)化曲線來代替。圖2給出了El Centro波作用下以加速度為優(yōu)化目標(biāo)時(shí)的典型進(jìn)化曲線。

對(duì)于所研究的地震波時(shí)程和阻尼器數(shù)量不同的每種工況，分別進(jìn)行3次優(yōu)化，平均計(jì)算時(shí)間約為6 500 s，合108min。第一階段和第二階段研究的優(yōu)化結(jié)果分別如表5和表6所示。

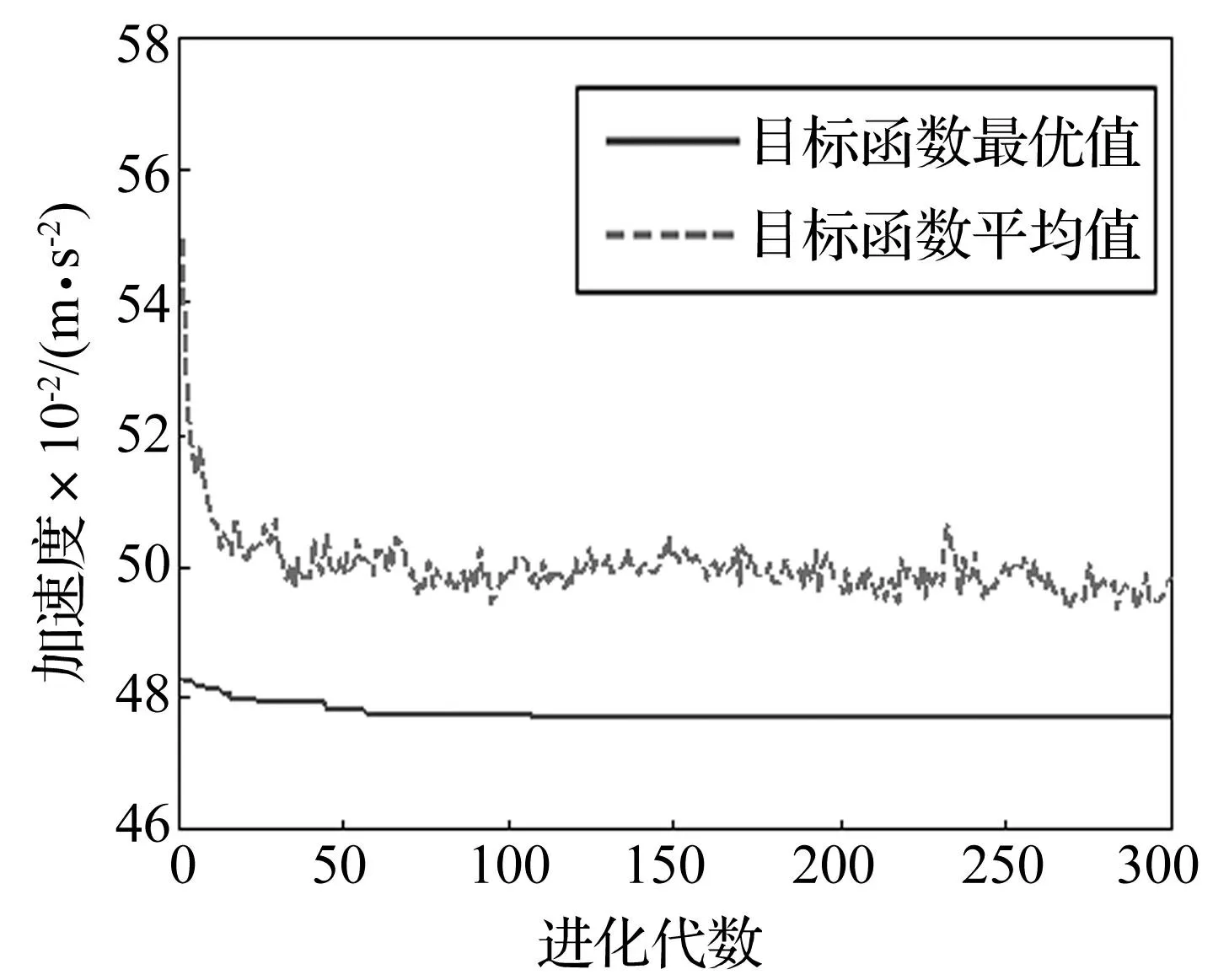
圖2　進(jìn)化曲線 Fig.2 Evolution curve

從表中可以看出，在不同的地震波作用下，以加速度為優(yōu)化目標(biāo)時(shí)，DSCGA顯然能夠獲得比SGA更好的加速度控制效果，其最優(yōu)解中存在一層布置多個(gè)阻尼器的情況。如在El Centro波作用下，第4、 5層分別布

表5　不同地震波作用下的優(yōu)化結(jié)果

表6　阻尼器數(shù)量不同時(shí)的優(yōu)化結(jié)果

置2個(gè)阻尼器；DEL AMO BLVD波作用下，第3、4、5層分別布置2個(gè)阻尼器；Northbridge波作用下，第3層布置3個(gè)阻尼器。由于二進(jìn)制編碼的SGA不能表示各層阻尼器布置數(shù)量不同的情形，無法搜索到這類可行解，因而其最優(yōu)解的控制效果明顯不如DSCGA。

從表6中阻尼器安裝數(shù)量不同時(shí)的優(yōu)化結(jié)果對(duì)比，可以看出一個(gè)明顯的趨勢，即阻尼器安裝的數(shù)量越多，DSCGA的優(yōu)勢越明顯。阻尼器數(shù)量為8個(gè)時(shí)，DSCGA與SGA的優(yōu)化效果一致，且基本集中在中下層；阻尼器數(shù)量為10個(gè)時(shí)，DSCGA的加速度優(yōu)化效果已經(jīng)開始優(yōu)于SGA；阻尼器數(shù)量為12個(gè)時(shí)，無論是加速度還是層間位移角，DSCGA的優(yōu)化效果都明顯優(yōu)于SGA，所獲得的最優(yōu)解中都存在一層布置多個(gè)阻尼器的情形。這是因?yàn)椋?dāng)阻尼器的數(shù)量較少時(shí)，最優(yōu)布置方案傾向于中下層均勻布置，其最優(yōu)解包含在SGA的可行空間中；當(dāng)阻尼器的數(shù)量較多時(shí)，各層阻尼器數(shù)量不同能起到更好的控制效果，其最優(yōu)解已經(jīng)超出了SGA可行解的范圍(即前文所述該問題的SGA編碼不具備完備性的缺點(diǎn))。而數(shù)值序列編碼的完備性使得DSCGA能夠順利查找到所需要的全局最優(yōu)解。

4結(jié)論與展望

針對(duì)具體的工程優(yōu)化問題，選用適當(dāng)?shù)木幋a和相應(yīng)的遺傳算子進(jìn)行優(yōu)化，是遺傳算法研究一個(gè)重要的方向。為求解高層結(jié)構(gòu)阻尼器優(yōu)化配置(允許各層安裝不同數(shù)量阻尼器)問題，本文提出了數(shù)字序列編碼(編碼方案B)及其相應(yīng)的DSCGA。

采用數(shù)字序列編碼直接目的是完備(completeness)且合法(legality)地表達(dá)的表現(xiàn)型空間，解決以往編碼方案不能完備表達(dá)表現(xiàn)型空間(方案C)或大量非法解破壞遺傳算法機(jī)理，導(dǎo)致GA陷入非法解陷阱(方案A、D)的問題。

與一般的整數(shù)編碼遺傳算法相比，DSCGA具有兩個(gè)明顯的創(chuàng)新之處：①數(shù)字序列編碼編碼充分考慮了各可選位置選用目標(biāo)數(shù)量不同(以高層結(jié)構(gòu)各層安裝不同數(shù)量阻尼器為例)的優(yōu)化問題的特點(diǎn)，具備合法性、Lamarckian性和優(yōu)良的因果性，解決了二進(jìn)制編碼SGA不能完備表達(dá)此類優(yōu)化問題的求解空間的問題；②DSCGA的編碼元素處于基于層次而非局部組分層次，僅具有序號(hào)意義，可以采用離散重組交叉算子進(jìn)行交叉，而非一般整數(shù)編碼遺傳算法所用的算術(shù)交叉。

DSCGA的意義在于提供了一種求解多個(gè)可選位置選用不等數(shù)量目標(biāo)的復(fù)雜優(yōu)化模型的方法。數(shù)字序列編碼可以完備且合法地表達(dá)此類優(yōu)化問題的表現(xiàn)型空間，這使得DSCGA的每一次搜索，也即每一個(gè)可行解的適應(yīng)度值計(jì)算都具備尋優(yōu)價(jià)值，不會(huì)陷入無謂的非法解陷阱；所用編碼與表現(xiàn)型空間的可行解一一對(duì)應(yīng)，不會(huì)錯(cuò)失優(yōu)化問題的全局最優(yōu)解。離散重組交叉算子的根本思想在于通過交叉將部分阻尼器的安裝位置換位，而非普通整數(shù)編碼遺傳算法所用算數(shù)交叉給出的數(shù)值運(yùn)算，更加符合此類優(yōu)化問題的優(yōu)化機(jī)理。

對(duì)20層Benchmark模型進(jìn)行阻尼器優(yōu)化配置的算例表明，DSCGA可以解決此類復(fù)雜的數(shù)值優(yōu)化問題。由于所用編碼與表現(xiàn)型空間的可行解一一對(duì)應(yīng)，既不會(huì)錯(cuò)過優(yōu)化問題的全局最優(yōu)解，也不會(huì)陷入無謂的非法解陷阱。整個(gè)優(yōu)化過程所用時(shí)間約6 500 s，在可接受范圍內(nèi)。

本文針對(duì)“小震不壞”設(shè)計(jì)階段，詳細(xì)研究了多遇地震作用下結(jié)構(gòu)的彈性響應(yīng)優(yōu)化。以此為基礎(chǔ)，該方法有望推廣到罕遇地震作用下進(jìn)入彈塑性階段的優(yōu)化分析。這部分工作將是本文后續(xù)研究的方向和重點(diǎn)。

參考文獻(xiàn)

[1]Li L, Song G, Ou J. A Genetic algorithm-based two-phase design for optimal placement of semi-active dampers for nonlinear Benchmark structure [J].Journal of Vibration and Control,2010(16):1379-1392.

[2]Estekanchi H E, Basim M C. Optimal damper placement in steel frames by the Endurance Time method [J]. TheStructure Design of Tall Special Buildings, 2011(20):612-630.

[3]楊佑發(fā)，李帥，熊麗. 偏心結(jié)構(gòu)黏滯阻尼器的空間位置優(yōu)化[J]. 土木工程學(xué)報(bào)，2012(45):99-102.

YANG You-fa, LI Shuai, XIONG Li. Optimal distribution of fluid viscous dampers for eccentric structure [J]. China Civil Engineering Journal, 2012(45)：99-102.

[4]田莉，陳換過，祝俊，等. 基于自適應(yīng)模擬退火遺傳算法的傳感器優(yōu)化配置研究[J]. 振動(dòng)工程學(xué)報(bào)，2012,25(3):238-243.

TIAN Li, CHEN Huan-guo, ZHU Jun, et al. A study of optimal sensor placement based on the improved adaptive simulated annealing genetic algorithms [J]. Journal of Vibration Engineering, 2012,25(3):238-243.

[5]Dyer J D, Hartfield R J, Dozier G V, et al. Aerospace design optimization using a steady state real-coded genetic algorithm [J]. Applied Mathematics and Computation, 2012(218):4710-4730.

[6]Panteleev A V, Metlitskaya D V. An application of genetic algorithms with binary and real coding for approximate synthesis of suboptimal control in deterministic systems [J].Automation and Remote Control, 2011(72):2328-2338.

[7]陳瑤，霍佳震. 整數(shù)編碼的組群遺傳算法在分組優(yōu)化中的設(shè)計(jì)和應(yīng)用[J]. 上海交通大學(xué)學(xué)報(bào)，2013,47(3):472-478.

CHEN Yao, HUO Jia-zhen. Number-coded grouping genetic algorithm for solving grouping problem: design and application [J]. Journal of Shanghai Jiaotong University, 2013,47 (3):472-478.

[8]Fujita K, Moustafa A, Takewaki I. Optimal placement of viscoelastic dampers and supporting members undervariable critical excitations [J]. Earthquake and Structures, 2010(1):43-67.

[9]李宏男，曲激婷. 基于遺傳算法的位移型與速度型阻尼器位置優(yōu)化比較研究[J]. 計(jì)算力學(xué)學(xué)報(bào)，2010,27(2):252-257.

LI Hong-nan, QU Ji-ting. Comparison of optimalplacement of displacement-based and velocity-based dampers using genetic algorithm [J]. Chinese Journal of Computational Mechanics, 2010,27(2):252-257.

[10]燕樂緯，陳洋洋，王龍，等. 基于相對(duì)適應(yīng)度遺傳算法的高層結(jié)構(gòu)黏滯阻尼器優(yōu)化布置[J].振動(dòng)與沖擊，2014,33(6):195-200.

YAN Le-wei, CHEN Yang-yang, WANG Long, et al. Optimum installation of viscous dampers in tall buildings based on relative fitness genetic algorithm [J]. Journal of Vibration and Shock, 2014,33(6):195-200.

[11]Su R K L, Yan L W.Provision of reinforcement in concrete solids using the generalized genetic algorithm [J].Journal of Computing in Civil Engineering, ASCE, 2011, 25(3): 211-217.

[12]徐趙東，馬樂為. 結(jié)構(gòu)動(dòng)力學(xué) [M]. 北京：科學(xué)出版社，2007.

[13]玄光男，程潤偉. 遺傳算法與工程優(yōu)化[M]. 北京：清華大學(xué)出版社，2004.

[14]Nakama T. Markov chain analysis of genetic algorithms applied to fitness functions perturbed concurrently by additive and multiplicative noise [J]. Computational Optimization and Applications，2012, 51(2):601-622.

[15]李敏強(qiáng)，寇紀(jì)淞，林丹，等. 遺傳算法的基本理論與應(yīng)用[M]. 北京：科學(xué)出版社，2002.

[16]Ohrori Y, Christenson R E, Spencer B F, et al. Benchmarkcontrol problems for seismically excited nonlinear buildings [J]. Journal of Engineering Mechanics, ASCE, 2004(130):366-385. L, Song G, Ou J. A Genetic algorithm-based two-phase design for optimal placement of semi-active dampers for nonlinear Benchmark structure [J].Journal of Vibration and Control,2010(16):1379-1392.