高速滾動球軸承動態載荷計算改進方法的研究

第一作者盛夏男，碩士生，1986年生

通信作者李蓓智女，教授，1955年生

高速滾動球軸承動態載荷計算改進方法的研究

盛夏，李蓓智，張亞偉

(東華大學機械工程學院，上海201620)

摘要：在離心力和陀螺力矩的作用下，滾動球軸承高速旋轉時的內部載荷分布與軸承靜止情況下的載荷分布具有顯著差異，其主要影響因素包括，滾動軸承的接觸角、軸承預緊位移以及旋轉速度等。基于Jones&Harris(簡稱J&H)力學模型的軸承載荷分布的分析方法已經得到了廣泛的應用。然而其計算公式多、迭代繁瑣、收斂速度慢。針對此現象，研究了軸承動態載荷分布規律及其算法，提出了改進的J&H軸承數值計算模型，給出相應的簡化計算步驟。計算與對比結果表明，改進的J&H計算模型在其應用范圍內，可以大幅減少計算時間。

關鍵詞：高速滾動軸承；動態載荷計算；數值計算簡化模型

收稿日期：2013-10-21修改稿收到日期：2014-02-14

中圖分類號:TH133.33文獻標志碼：A

A simplified approach for calculation of rolling ball bearing internal dynamic load distribution

SHENGXia,LIBei-zhi,ZHANGYa-wei(Research Center of Advanced Manufacturing Technology, College of Mechanical Engineering, Donghua University, Shanghai 201620, China)

Abstract:Rolling elements in a high speed rolling bearing are influenced by centrifugal force and gyroscopic effect its internal load distribution is quite different from that of a static bearing. The main influencing factors include bearing contact angles, axial preload and bearing rotation speed, etc. The method of calculating the distribution of bearing internal loads based on Jones & Harris (J&H) model is widely used. However, it involves too many equations, complicated iterations and slow convergence speed. Here, the law and algorithm of bearing internal load distribution were studied to simplify J&H bearing model. A new simplified calculation procedure was provided. The computation results showed that the improved J & H approach can reduce the calculation time significantly in its application range.

Key words:high speed rolling bearing; calculation of dynamic load; simplified model

滾動軸承是重要的旋轉機械基礎件，通常被稱為"工業的關節"，其重要性顯而易見[1]。尤其對于高速、精密機床，滾動軸承的工作精度很大程度上決定了機床的加工精度。很多學者[2-3]開展了高速主軸-軸承系統的研究。 隨著制造業對機床精度和速度越來越高的要求，滾動軸承的相關研究也越來越廣泛，尤其是在轉子動力學方面，軸承在高速運轉時的動態性能受到了各個學者的關注[4-6]。Hertz首先提出了用于滾動軸承力學分析的接觸理論，Jones[7]最先以Hertz接觸理論為基礎，建立了滾動軸承動態力學分析的擬靜力學模型，并在軸承力學平衡方程中引入了慣性力效應；Harris在Jones的基礎上提出了更完善的軸承計算模型，其中考慮了高速運轉時，滾球的陀螺效應，并建立了經典的Jones & Harris滾動軸承內部動態載荷數值計算模型[8]，Jones和Harris都采用了擬靜力學法，該計算模型易于編程和計算，且被相關實驗驗證了其準確性，因此，一直被不斷地發展并應用至今。 Gupta[9]考慮了滾球的運動狀態、受力狀態以及各零件之間的相互作用關系, 提出了滾動軸承受力分析的動力學模型。然而Gupta的模型所采用的微分方程在使用計算機編程計算時過于復雜，限于當時的計算機水平而沒有很好的得到發展。

J&H軸承模型涉及了相當數量的非線性方程組，并且一些計算參數之間有非常強的耦合性，一些計算參數在迭代的過程中需要重復使用從而造成迭代收斂過慢的情況[10-11]，根據文獻[10-11],基于J&H模型進行了大量數值計算的測試后，認為該模型的收斂性和計算速度有待進一步改善和提高，尤其是用于分析高速軸承[12]。同樣，唐運冰等[13]也曾提到，在計算滾動軸承動態載荷分布以及進一步分析其動力學性能時，容易發生收斂困難，振蕩等不利因素，并建議加入松弛系數。為此，本文將分析Jones & Harris軸承模型的不足，研究軸承動態載荷分布規律及其計算方法，提出相應的改進方法與模型，以提高高速滾動球軸承動態載荷分布的計算分析的效率。

1Jones & Harris滾動軸承動態模型簡述

1.1Jones & Harris模型

圖1　軸承滾球方位角及其序號定義 Fig.1 Azimuth of rolling bearing

Jones & Harris模型(以下簡稱為J&H模型)假設軸承相鄰滾球間隔的角度均等，即該角度恒為Δφ。每個滾球對應序號q如圖1所示，并稱φq為第q個滾球的方位角，滾球總數為Z，則Δφ=2π/Z。滾動軸承在高速轉動時(一般為轉速大于20 000 r/min或dmn大于5×105)，受到發生公轉與自轉的滾球將受到離心力和陀螺效應的作用，使滾球與滾道間的位置關系與軸承處于靜止時有明顯差異。圖2為滾動軸承靜止時滾球與滾道的橫截面示意圖，其中，BD表示內外滾道曲率中心的距離，BD=ro+ri-D=(fo-fi-1)D。對于滾動軸承，fo和fi分別是軸承外滾道，內滾道的曲率半徑系數，通常為0.50～0.54。軸承在未受到任何載荷時的接觸角為α0。

圖2　單個滾球與滾道的靜態接觸 Fig.2 Static contact between a ball and raceways

軸承在旋轉時，滾球與滾道的接觸點發生變化，其位置關系及接觸角的變化如由圖3所示，內接觸角αiq增大而外接觸角αoq減小；由于離心力和陀螺力矩的作用產生了滾球與滾道的接觸變形δiq及δoq；(內滾道處的陀螺力矩被滑動摩擦抵消)，同時，在外載荷和滾球的共同作用下，軸承內圈產生位移變化(反映在內滾道曲率中心的變化上)。

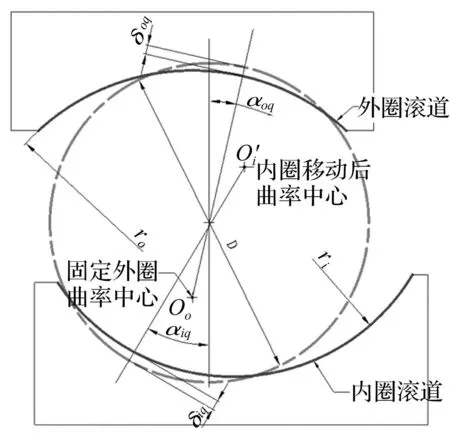
圖3　轉動滾球與滾道的動態接觸情況 Fig.3 Contact between rotating ball and raceways

通過圖4的描述可以清晰地觀察軸承旋轉時某個滾球與滾道之間的幾何關系與變形協調關系。圖中δrq，δa為內圈徑向與軸向的變形量。Oo，Ob以及Oi分別為軸承靜止時的外滾道曲率中心、滾球中心和內滾道的曲率中心。和Oi′和Ob′分別為軸承旋轉時滾球與內滾道曲率中心發生偏移后所處的位置。αiq,αoq為軸承的動態內、外接觸角。軸承轉速和外載荷的變化都會使Oi′，Ob′，αiq，αoq隨之變化。為了求得這些變化量或計算軸承內圈整體的偏移量，需要建立一系列的關系式來求解。

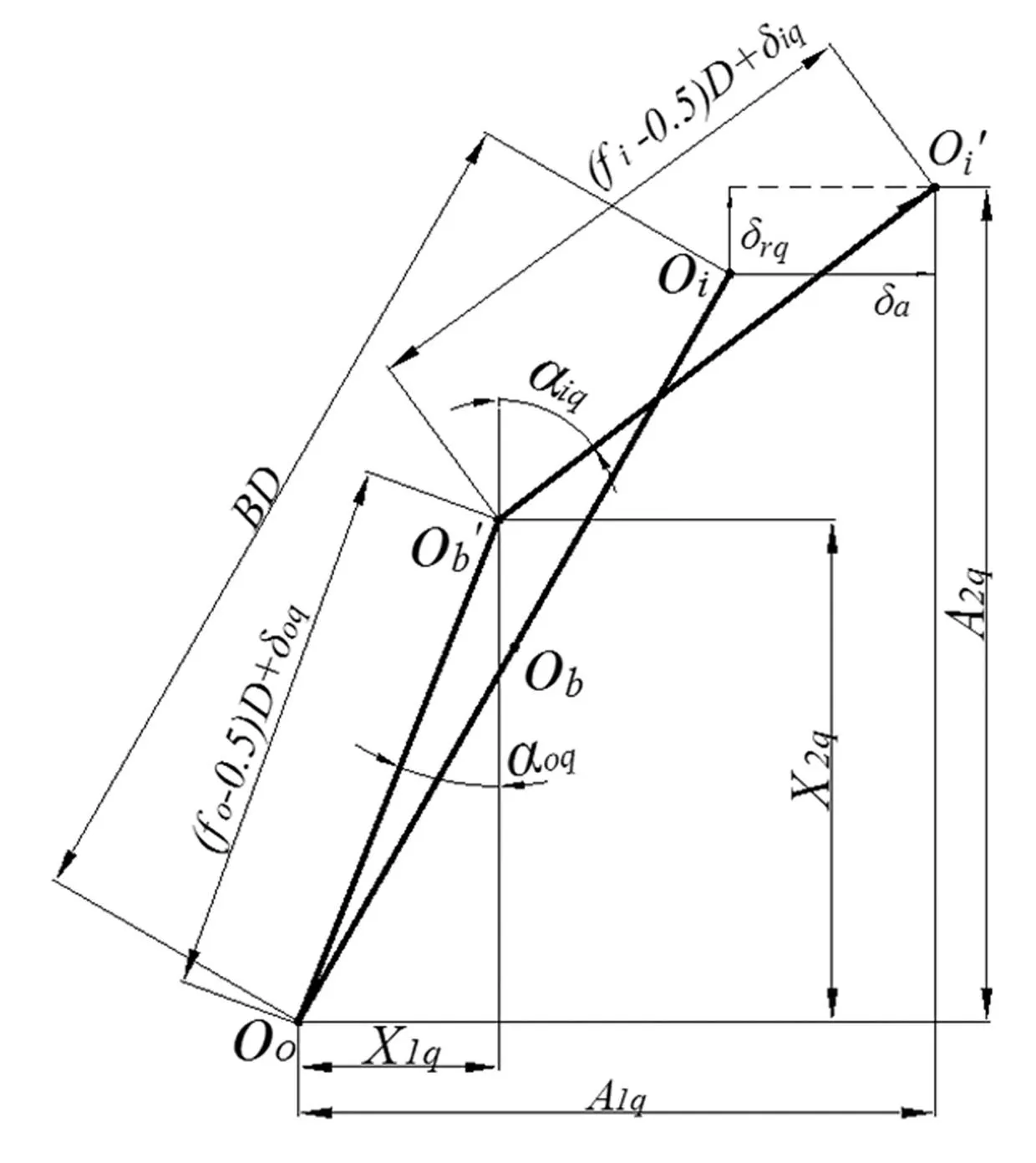
圖4　滾球與滾道的接觸情況幾何關系圖 Fig.4 Geometry relations between rollingelement and raceways

根據圖4，相關關系式由式(1)～(8)所示。

(1)

(2)

A1q=BDsinα0+δa

(3)

A2q=BDcosα0+δrq

(4)

據式(1)～(4)可以解得αiq，αoq的三角函數值：

(5)

(6)

結合圖4和式(1)～(5)通過勾股定理建立等式：

(A1q-X1q)2+(A2q-X2q)2-

[(fi-0.5)D+δiq]2=0

(7)

(8)

根據滾球的受力平衡(圖5)可得到：

Qiqsinαiq-Qoqsinαoq-

(9)

Qiqcosαiq-Qoqcosαoq-

(10)

圖5　滾球的受力 Fig.5 Loads on the ball

其中:Qiq和Qoq為Hertz接觸力，Fcq，Mgq為該方位角滾球所受的離心力和陀螺力矩，這些量計算方法可參考文獻[14]。

方程(7)～(10)僅反映軸承中第q個滾球與內外圈的相互作用情況。將所有滾球對軸承內圈的接觸力進行求和，還可以建立如下平衡方程：

(11)

(12)

式中:Fr和Fa表示作用在軸承內圈的徑向和軸向外部載荷，Z為軸承內含的滾球數。

1.2J&H模型的計算過程及其不足

式(7)～(10)以及(11)、(12)構成了Jones & Harris軸承動態載荷分布計算模型。方程組中總共未知變量為4Z+2個，其中方程組(7)～(10)包含4Z個未知量，(11)、(12)包含兩個未知量。同時，該數值計算模型總共包含4Z+2的方程數。因此，在理論上方程組有解，通過迭代法可以得到其近似解。在該計算模型中的未知量并非固定不變，可以根據要求設定未知量。Jones 和Harris 都以X1q、X2q、δiq、δoq以及δrq和δa(其中X1q、X2q表示滾球在X,Y方向的偏移位移量，δiq、δoq分別表示內外滾道接觸變形量，δrq和δa則分別表示內圈的軸向及徑向變形量)為未知變量。然而經過計算發現，δrq和δa并不適合作為未知量，他們對于給定量Fr和Fa的大小極為敏感，極易造成數值計算的不穩定[12]，采用Fr和Fa作為未知變量可以極大地提高方程組的收斂性，更有利于方程組的求解。因此，本文中的數值模型采用這種未知量設定方法。顯然，在該計算模型中都是非線性方程組，可以看出某些變量如：cosαiq與X2q等在方程組中有非常強的耦合性，且對數值變化敏感。加上方程數目較多，計算過程非常復雜且費時。

2改進的J&H計算模型

2.1改進模型的假設

對于由4Z+2個等式所構成的非線性方程組來說其計算過程必然顯得過于繁瑣和費時。因此若能合理簡化方程或減少方程組的數目，可使模型的計算效率得到顯著提升。

首先，構成多達4Z個方程原因是式(7)～(10)中的參數會根據每個滾球方位角的不同而改變。對于任意第q個位置的滾球，若令δrq=0即假設沒有徑向力作用于軸承內圈。這樣，對于軸承中每個方位角的滾球，所有的變量都相同，式(7)～(8)所組成的方程組是完全相同的。因此在這個前提下，只需計算對應任意方位角的(7)～(10)式，就可以得到所有方位角的解。

根據這點可以把軸承在高速旋轉時滾道與滾球的變形分解為兩個階段進行：

圖6　Jones & Harris 模型簡化的兩個步驟 Fig.6 Two steps of simplifying the Jones & Harris’s model

第一階段：首先不考慮徑向力載荷對軸承內圈的作用，即先認為δrq=0。由式(7)～(10)計算出X1q、X2q、δiq、δoq(按任意方位角的滾球計算均可)。顯然，如果不考慮徑向力的作用，軸承內圈的徑向位移為0，計算結果同樣如此。圖6 (a)表示了這一過程，軸承內圈曲率中心由原先處于靜平衡狀態下的Oi軸向平移到Oi′，并在這個位置達到平衡狀態；滾球與內外滾道產生接觸變形δiq、δoq；同時滾球中心從Ob偏移到Ob′。

第二階段：在步驟1的基礎上重新將原有的徑向力加入到計算中。此時，原先處于平衡狀態的滾球與滾道會再次發生位置上的偏移，滾球中心Ob′移動到Ob″,而內圈滾道的曲率中心Oi′則偏移到Oi″。圖6(b)著重反映了這個過程。

(13)

同時第二階段滾球的靜力平衡公式為：

(14)

(15)

通過這樣對J&H軸承模型的簡化，計算方程數由4Z+2縮減到2Z+6，其中2Z個方程為對應不同滾球方位角的式(14)與(15)，另外“4+2”個方程為方程組(7)～(10)，這4個等式中的δrq=0；以及式(11)和(12)。顯然，模型簡化后方程數目幾乎減少一半，且式(14)與(15)的參數之間耦合度明顯較J&H軸承模型的更弱，并且無需使用Newton迭代法就可以得到結果。在J&H模型當中時常會遇到迭代收斂慢的情況，而簡化后的模型對此則大為改善。

2.2改進方法的可行性分析

對于簡化J&H軸承模型，上文提出了兩個關鍵的假設。其一是考慮徑向力對軸承內圈的作用與否都不會對動態外接觸角αoq產生影響。其二假設認為徑向力作用以及其作用的大小不會對滾動軸承的軸向位移造成影響。現對這兩個假設的可行性進行分析。

以高速滾動軸承B7005C/P4為例，其軸承基本參數由表1所示。

可行性分析一：由圖7可以看出徑向力及其大小對于動態外接觸角的余弦值的影響。在低于9 000r/min時，可以看到徑向力對外接觸角具有一定的影響，無徑向力作用和1 000 N徑向力作用差別可達0.009(該誤差值為cosαoq誤差百分比的1%左右)。但當軸承轉速超過10 000 r/min時，徑向力對cosαoq影響逐漸減弱，當轉速達到12 000 r/min時，差別已經可以縮小到0.002(該誤差為本身值的0.2%)，即在式(14)中用無徑向力的cosαoq取代有徑向力的相應值，其誤差大約為1%～0.2%。因此，改進的J&H模型尤其適用于高速軸承。

表1　B7005C/P4高速球軸承基本參數

圖7　不同轉速下徑向力與軸承外接觸角余弦值的關系 Fig.7 Influences of radial forceand various speeds on cosα oq

可行性分析二：文獻[14-15]的相關討論認為，對于軸承內圈受到純徑向力作用時，內圈產生的軸向位移可以忽略不計。此外，高速機床的軸承的預緊力能夠將軸承內圈保持在一定的位置，若機床采用多組軸承的配置方法，如“背靠背”或“面對面”等也能約束軸承內圈的軸向位移。因此，在改進的J&H模型的計算過程中忽略徑向力對軸向位移的影響也是可行的。

3案例分析

以B7005C/P4高速球軸承為例(見表1)，分別使用J&H和改進的J&H計算模型對該軸承的高速旋轉時的動態參數進行計算和對比分析，以驗證改進的J&H計算模型的有效性。由于假設軸承外圈定，且都采用外滾道控制理論，則軸承外滾道動態參數δoq和cosαoq對軸承的動態特性影響并不明顯，分析中主要針對內滾道的動態特性參數δiq和cosαiq。數值模型由Matlab進行編程與計算，兩種軸承模型的計算結果由圖8～圖11給出。

圖8、圖9分別為徑向力Fr=100 N和Fr=300 N時內滾道接觸變形值δiq的計算分析結果。結果顯示，顯然較小的徑向載荷Fr情況下，改進的J&H模型與J&H模型計算結果的差異非常之小，當軸承轉速高于9 000 r/min時，可將計算結果的差異控制在0.2%以內。因此改進的J&H模型在計算高速輕載機床滾動軸承動態特性時，能完全替代J&H軸承模型。

圖8　徑向力F r=100 N時不同轉速下δ iq計算結果對比 Fig.8 Comparison of δ iq under different speed with F r=100 N

圖9　徑向力F r=300 N時 不同轉速下δ iq計算結果對比 Fig.9 Comparison of δ iq under different speed with F r=300 N

圖10　徑向力F r=100 N時不同轉速下cosα iq計算結果對比 Fig.10 Comparison of cosα iqunder different speed with F r=100 N

圖10和圖11給出了Fr=100 N和Fr=300 N時內滾道動態接觸角cosαiq在相關轉速下的計算分析結果。顯然，除6 000 r/min時兩種模型的cosαiq計算結果有誤差外，其它轉速下兩者計算結果數值差異不超過1%。

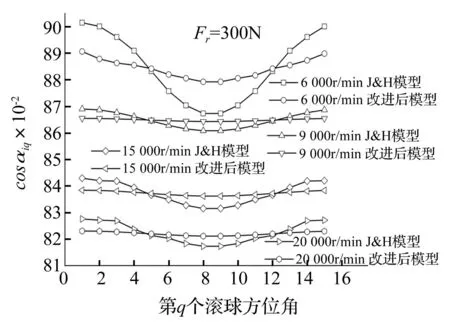
圖11　徑向力F r=300 N時 不同轉速下cosα iq計算結果對比 Fig.11 Comparison of cosα iqunder different speed with F r=300 N

4結論

本文分析和計算了軸承高速旋轉情況下的載荷分布，研究了軸承動態載荷分布規律及其計算方法，提出了改進的J& H軸承數值計算模型，避免了Jones 和 Harris(J&H)計算模型需要對大量非線性方程組進行迭代計算，不僅提高了計算效率，同時也弱化了參數之間的耦合程度。以B7005C/P4、(最好再給一種分析過的型號)等高速球軸承為對象，并根據相關高速軸承的實際工作要求，進行了相應的計算與分析，對比結果表明了，改進的J&H計算模型，可以使計算工作效率提高2～3倍(見圖12)。

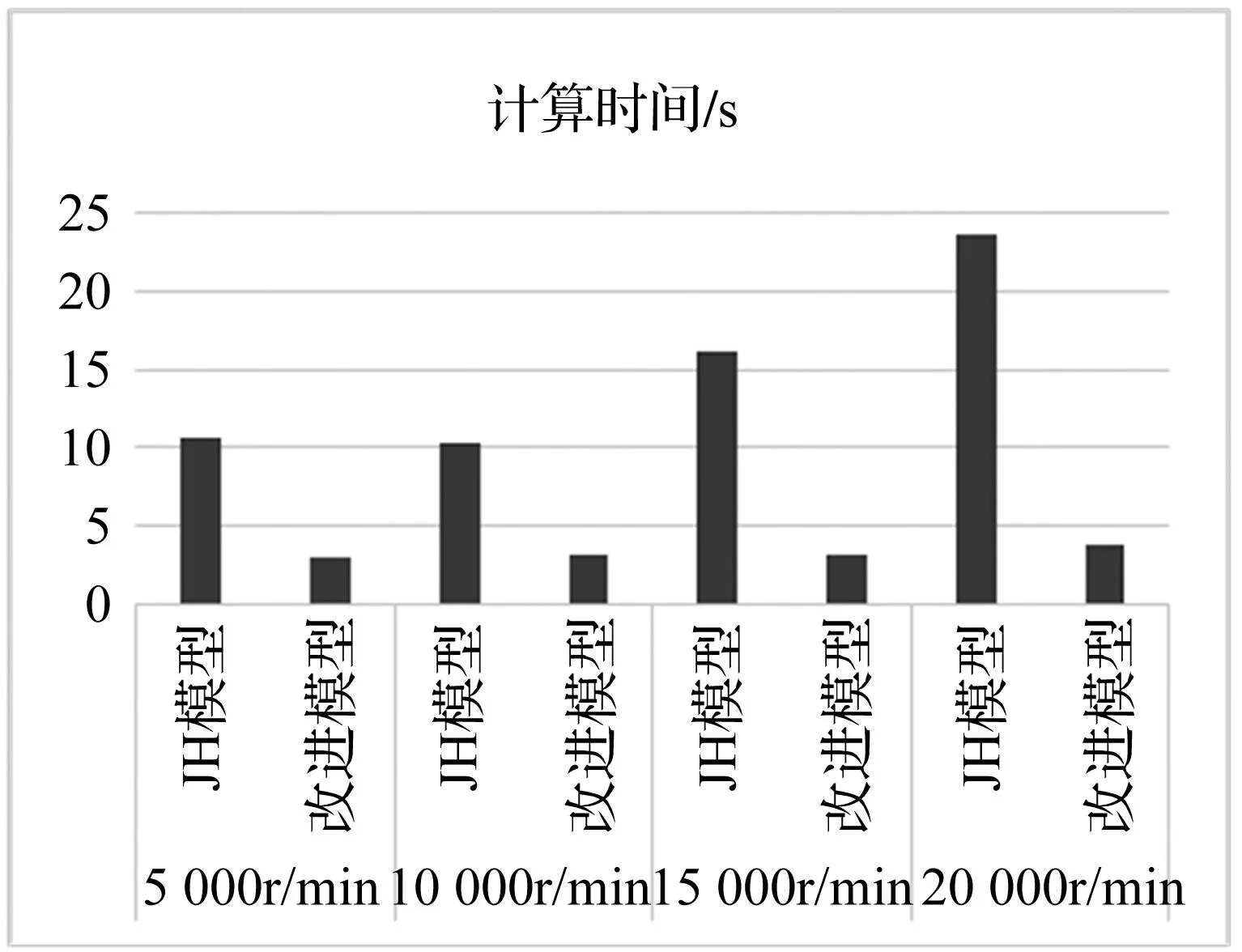
圖12　J&H模型與改進J&H模型的計算時間比較 Fig.12 Comparison of calculation speeds between J&H model and simplified J&H model

當滾動軸承低速旋轉時，改進的J&H模型與J&H模型的計算結果最大存在8%的差異，但是軸承轉速在9 000 r/min或以上時，滾動軸承動態載荷分布的計算結果差異始終小于1%。誤差產生是由于在改進模型的假設中，始終認為外接觸角不變而造成的，實際上，軸承運行速度很高時或者徑向載荷不大時，外接觸角的變化可以忽略。因此，在分析高速輕載機床的滾動軸承時，改進的J&H模型具有明顯的計算分析優勢。

參考文獻

[1]楊曉蔚, 周宇. 滾動軸承重要性與技術含量縱論[J]. 軸承,2003(1): 35-38.

YANG Xiao-lan, ZHOU Yu. Discussion on the Importance and technology of the rolling bearing[J]. Bearing,2003 (1): 35-38.

[2]Gunter E J. Dynamic stability of rotor-bearing systems: Scientific and technical information division[J]. National Aeronautics and Space Administration, 1966.

[3]Mechanical, Tecnmologyinc, Lathamny.Rotor-bearing dynamics design technology Part IV: [M].1965.

[4]Cao Yu-zhong, Altintas Y. A general method for the modeling of spindle-bearing systems[J]. Journal of Mechanical Design, 2004, 126(6): 1089.

[5]Sinou J J. Non-linear dynamics and contacts of an unbalanced flexible rotor supported on ball bearings[J]. Mechanism and Machine Theory,2009, 44(9): 1713-1732.

[6]Bai Chang-qing, Zhang Hong-yan, Xu Qing-yu. Subharmonic resonance of a symmetric ball bearing-rotor system[J]. International Journal of Non-Linear Mechanics, 2013, 50: 1-10.

[7]Jones A B. Ball motion and sliding friction in ball bearings[J]. Journal of Basic Engineering,1959,81:1-12.

[8]Harris T A,Mindel M H. Rolling element bearing dynamics[J]. Wear, 1973, 23: 311-337.

[9]Gupta K. Advanced dynamics of rolling elements[M]. Springerverlag; 1984.

[10]朱益利, 金超武, 許磊,等. 滾珠軸承力學模型的數值求解方法研究[J]. 中國機械工程,2013(4): 427-431.

ZHU Yi-li, JIN Chao-wu, XU Lei, et al. Methods of ball bearing mechanics model[J] China Mechanical Engineering,2013(4): 427-431.

[11]趙春江, 孫永春, 王建梅. 高速角接觸球軸承接觸角的求解分析[J]. 軸承, 2008(10): 1-4.

ZHAO Chun-jiang, SUN Yong-chun, WANG Jian-mei. Analysis on contact angle of high speed augular contact ball bearings[J]. Bearing,2008(10): 1-4.

[12]Liao Neng-tung, Lin Jen-fin. Ball bearing skidding under radial and axial loads[J]. Mechanism and Machine Theory,2002,37:91-113.

[13]唐云冰, 高德平, 羅貴火. 航空發動機高速滾珠軸承力學特性分析與研究[J]. 航空動力學報, 2006, 21(2): 354-360.

TANG Yun-bing,GAO Ge-ping,LUO Gui-huo. Research of aero-engin high-speed ball bearing[J]. Journal of Aerospace Power,2006, 21(2): 354-360.

[14]Harris Tedric A. Rolling bearing analysis[J]. John Wiley & Sons. INC, 2001.

[15]Palmgren A. Ball and roller bearing engineering, 3rd ed[M]. Burbank, Philadelphia: SKF Industries Inc., 1959.