輸電塔氣動力系數和氣動導納風洞試驗研究

第一作者鄧洪洲男，博士，教授，1960年生

通信作者胡曉依女，博士，講師，1970年生

輸電塔氣動力系數和氣動導納風洞試驗研究

鄧洪洲， 司瑞娟， 段成蔭， 胡曉依

(同濟大學建筑工程系,上海200092)

摘要：輸電塔結構的非定常抖振力與來流風速之間存在復雜的非線性關系，基于風洞試驗得到的某1000kV格構式直線輸電塔彈性模型的基底力以及參考高度處同步采集的風速時程，采用線性和高斯兩種近似假定計算了非定常氣動力系數并與試驗值進行了比較；提出了包含結構氣動阻尼效應在內的總氣動導納的概念，通過基底脈動力譜和來流脈動風速譜的比值對總氣動導納函數進行識別，并用基于頻域相干函數對導納函數的線性部分進行了估計。結果發現，風偏角線性近似所計算靜氣動力系數的偏差較高斯近似小；由于氣動抖振力非定常性質明顯，不考慮總氣動導納函數將高估輸電塔模型的抖振響應；脈動風力與脈動風速間有較強的非線性關系，用線性導納函數計算的抖振力譜將低估脈動風分量的影響。

關鍵詞：輸電塔；風洞試驗；氣動系數；氣動導納；抖振響應

收稿日期：2013-09-30修改稿收到日期：2014-01-09

中圖分類號:TM753；TU317+.1文獻標志碼：A

基金項目：軍隊科研資助項目([2012]80)

Wind tunnel test for aerodynamic coefficient and aerodynamic admittance of a transmission tower

DENGHong-zhou,SIRui-juan,DUANCheng-yin,HUXiao-yi(Department of Building Engineering, Tongji University, Shanghai 200092, China)

Abstract:Buffeting forces of structures, such as, transmission tower usually have a complex nonlinear relation to incoming wind fluctuations. Based on wind forces and simultaneous fluctuating wind speed time history measured from a wind tunnel test on a model of 1000 kV suspension transmission tower, the aerodynamic coefficients and aerodynamic admittance functions of the tower were studied. Unsteady aerodynamic coefficients obtained in the test were compared with those estimated starting from linear and Gaussian assumptions. The concept of total aerodynamic admittance including structural aerodynamic damping effect was proposed. It was identified with ratio of power spectral density of wind force to that of fluctuating wind speed. The linear admittances representing correlated parts of the wind speeds and wind forces were estimated by employing frequency-domain coherence functions. Results showed that the linear assumption of relationship between time-dependent wind angle of attack and associated aerodynamic coefficient has a higher accuracy than that of Gaussian assumption; because of the unsteady nature of wind-speed-to-wind-force relation, neglecting aerodynamic admittances leads to higher estimation of the buffeting responses of the tower; moreover, the effects of wind fluctuations are underestimated with linear admittances in spite of the stronger nonlinearity between wind speed and wind force.

Key words:transmission tower; wind tunnel experiment; aerodynamic coefficient; aerodynamic admittance; buffeting response

隨著高度的增加，輸電塔的柔性越來越大，對作用其上的風荷載也更加敏感。這導致輸電塔的抖振響應顯著增大，這些風振響應反過來會引起結構應力的大幅增加或結構構件連接的疲勞損傷的累積。顯然，對強風下輸電塔抖振響應的準確預測對結構設計都有著至關重要的意義。

氣動導納函數一直是結構抖振分析的重要參數。一般來講，結構所受氣動力大多基于線性準定常模型計算，認為脈動風與氣動力的傳遞函數不隨時間和頻率變化，忽略脈動風的高階項貢獻而近似取泰勒展開線性項。事實上，結構上脈動風力不但和風向角(脈動風的線性項)有關，還可能與脈動風分量之間存在高度非線性[1]。對某344m桅桿的實測結果顯示，當湍流度小于15%時略去脈動風高階項產生的偏差較小，而湍流度達到25%時 計算結果的誤差將達20%左右[2]。

在對細長的橋梁結構研究中，導納函數可采用直接法計算[3-4]，通過脈動風力功率譜和脈動風速功率譜的比值求得。Peil等[2]對測量結果的線性和非線性導納函數進行了識別，計算了根據湍流分量修正的風力譜。Snaker等[5]則是通過高頻測力天平測得的抖振力譜和熱線風速儀測得的風速譜求得了兩次多項式形式的氣動導納函數。為提高識別精度，趙林等[6]采用互譜識別法對大跨度橋梁節段模型的導納函數進行了識別，并采用雙對數三次多項式的形式對結果進行了擬合。本文基于對一1000kV輸電塔氣彈模型的天平測力試驗結果，通過對模型基底抖振力和來流脈動風速功率譜的測量，采用直接法對格構式輸電塔架的氣動導納函數在頻域內進行了識別,并對阻力系數和升力系數進行了討論。一般來講，輸電塔為多孔的格構式結構，可認為其上的風荷載氣動力主要為阻力，但已有的風洞試驗結果表明[7-8]，湍流風作用下輸電塔架可產生明顯的橫向升力。

1試驗設置和測量

1.1氣彈模型設計

原型輸電塔的三維尺寸為19.12m×19.12m×105.4m，名義高寬比為5.373。橫擔支撐為等邊角鋼桿件，塔身主材和橫擔主材為鋼管。氣彈模型采用離散剛度法[9]設計，表1給出了模型的主要縮尺比(模型/原型)情況。

輸電塔采用毛細銅管加輕質外衣制作，模型高1.757m。模型的風洞阻塞比<1%，不需要考慮風洞阻塞修正。采用人工激振法測量模型的動力特性，模型在順導線方向和垂直導線方向上的基本頻率比較相近，分別約為20.2Hz和20.4Hz，兩方向阻尼比相差很小，基本在1.6%左右，扭轉頻率為28Hz。

表1　試驗模型的主要相似參數

1.2風洞設施

試驗在同濟大學邊界層風洞試驗室進行，風洞試驗段長15m、寬3m、高2.5m，可調風速范圍為1～68m/s。試驗分別在均勻流場和紊流場中進行，均勻流場紊流度<1%，湍流風場采用尖劈+粗糙元的方式進行模擬，試驗風場見圖1。

本次試驗中，試驗風場模擬的是開闊地面的自然風特性，平均風速剖面參考中國荷載規范[10]的A類地貌，冪指數α=0.12，紊流度參考國際風荷載標準[11]的取值，即30m高度處(模型0.5m高度)紊流度大致與風剖面冪指數相當。圖2為測得的縱向風速功率譜，其中擬合譜形如：

圖1 試驗平均風速廓線和紊流度剖面Fig.1Profilesofwindvelocityandturbulenceintensity圖2 縱向(a)和橫向(b)脈動風速功率譜Fig.2PSDofthelongitudinal(a)andtransverse(b)componentsoffluctuatingwind

1.3試驗說明

模型的基底抖振力響應使用五分量高頻測力天平進行測量，在參考高度處(橫擔下平面，距地面zr=1.02m)采用熱線風速儀測量來流風速的湍流分量，采用皮托管對風速進行輔助監測，皮托管布置于風洞邊緣參考高度處，用于控制平均風速。試驗數據的采樣頻率為200Hz，采樣時長81.915s。

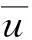
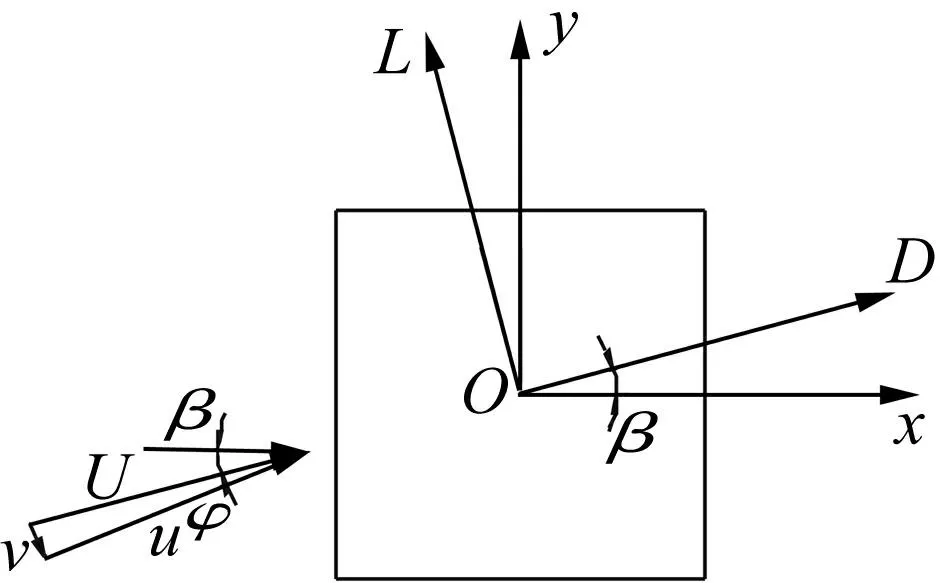
D=Fx·cos(β)-fy·sin(β) L=Fx·sin(β)+fy·cos(-β) U= u= +u′,v=v′ φ′?v/u 圖3　坐標定義 Fig.3 Coordinate systems

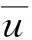
1.4基本假定

抖振力系數和氣動導納函數的求解基于如下假定：所有試驗得到的時程均視為穩態隨機過程；在計算抖振力系數時，認為平均抖振力僅由平均風速產生，脈動風速引起的抖振力視為零均值過程；縱向抖振力譜為縱向風脈動分量的函數，橫向抖振力譜為橫向風脈動分量的函數；將抖振力等效視為作用于動力風荷載、模型慣性力與阻尼力合力作用點；不計縱向和橫向脈動風的相關性。

1.5總氣動力譜的定義

高頻測力天平試驗要求模型剛度無限大、質量無限輕。但是，實際上對于輸電塔這一類高聳結構來說，制作出完全剛性的模型是很困難的。本文采用的氣彈模型即為非完全剛性的模型，模型-天平系統的基頻約20Hz，本文稱這種非完全剛性的模型為半剛性模型。為求得半剛性模型上的抖振風力荷載，文獻[12]提出一種消除由模型振動產生的慣性力作用的方法，本文稱這種消除了結構慣性力后的抖振力為總氣動力荷載。

計算時，將抖振力等效視為作用于一點，則動力風荷載產生的基底氣動彎矩可表示為：

M0(t)=F0(HT,t)HT

(1)

其中:M0(t)風荷載產生的模型基底彎矩，F0(t)風荷載產生的模型基底剪力，HT為模型等效高度,HT=σM0/σF0。

對半剛性的輸電塔模型，基底彎矩可表示為總氣動力產生的彎矩M(t)和慣性力產生的彎矩MI(t)之和，即

(2)

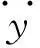
(3)

其中頻響函數為

(4)

式中:ω0為模型頻率，ζ為結構的阻尼比。

這樣，氣彈模型振動產生的慣性力即被消除，根據式(1)和式(3)求得結構上的總氣動力譜如下：

(5)

2抖振力和抖振力系數

2.1系數的定義與計算

取模型總高H，底部寬度B和0度風向構件的總迎風面積A為計算參數。fx,fy,mz,mx和my為模型坐標系xoy下的5個力分量。D和L分別為阻力和升力。則平均風力系數可按下式計算：

(6)

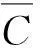
2.2靜態氣動力系數

通過均勻流場和紊流場中的測力試驗，根據式(6)，可求得模型坐標系xoy下的五分力系數(圖4(a)～(b))和風軸坐標系DOL下的阻力和升力系數(圖4(c))。

模型坐標系下平均抖振力系數的最大值出現在15°或75°風向角。這意味著，對輸電塔來說，沿其主軸方向(X、Y向)的最大力由和該主軸呈15°角的風產生。紊流場中測得的平均力系數和均勻流結果有著相近的分布規律，但紊流場中的靜力系數要明顯小于均勻流場時的值，均勻流場的阻力系數約在1.9～2.3之間，而紊流場的阻力系數在1.2～1.6之間，原因可能是兩種流場中雷諾數效應的影響不同，紊流使得流體分離層更加容易再附，從而導致阻力系數往往比均勻流場中小，下文將就此討論。

對模型在兩種流場中0～90°(垂直導線方向)風向角下阻力和升力靜力系數的比較發現兩種流場中阻力和升力系數依舊有相似的規律，紊流場中阻力系數明顯小于均勻流場，升力系數二者相近且數值不大，基本在0.2以內。對本次試驗的模型，其主要桿件的雷諾數比原型結構的雷諾數小2～3個數量級左右，由于對縮尺模型雷諾數的模擬難于實現。眾所周知，均勻流中的雷諾數效應比紊流中明顯得多，為考察雷諾數效應的影響本文根據獻[7]中給出的均勻流中圓截面桿件方形塔架不同雷諾數下的阻力系數情況對試驗結果進行修正，由實度比查得修正系數約0.75，對均勻流場中的試驗結果進行修正，修正后的結果即可被認為是考慮了雷諾數效應的桿件的阻力系數。修正后的均勻流中阻力系數和紊流場中測得的阻力系數曲線非常接近，和程志軍等[13]對某輸電塔氣彈模型的試驗結果也不謀而合。該現象至少可以說明兩個問題：一是格構式輸電塔的整體阻力系數值基本在某一個數值附近，而不隨輸電塔結構外形的變化而有很大的變化；二是對于紊流場中的格構式輸電塔架來說，雷諾數的影響較小，基本可以不予考慮。

圖4　模型坐標系xoy下的均勻流場靜力系數(a)、紊流場靜力系數(b)以及風軸坐標系DOL下的靜力系數比較(c) (C D,C L為均勻流場的結果；C t D,C t L為紊流場的結果；Modified C i為均勻流場修正Reynolds效應的結果；Ref 為文獻[13]的結果) Fig.4 Model’s force coefficients in xoy in uniform (a) and turbulent (b) flow, and model’s force coefficients in DOL (c) (C D,C Lare results in uniform flow; C t D,C t L are results in turbulent flow; Modified C i are results in uniform flow considering Reynolds effect; Ref is the tested results by Cheng(2000))

2.3抖振氣動力系數

根據圖4所示坐標系，隨風偏角和時間變化的縱向和橫向的風力可表示為式(7)的形式:

(7)

(8)

抖振氣動力系數Ci是和時間有關且隨φ′而變化的量，和脈動風速相似，也可以分成平均值和以該風向角為中心波動的脈動分量兩部分。取Ci泰勒展開的線性項可得：

Ci(β,φ′)=

(9)

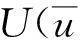
(10)

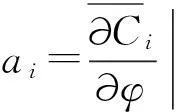
按線性假設和高斯假設兩種情況，根據試驗測得的脈動風速時程u(t)和v(t)對抖振氣動力系數按式(9)進行近似計算，并與式(7)計算的試驗值進行比較如圖5～圖6所示。從圖5的概率密度分布可以看出，試驗值比兩種假定下近似計算的方差要小。不同的假設條件主要導致氣動力系數方差的差異，對均值的影響微乎其微。對本次試驗模擬的風場來說，用高斯假定估算的氣動力系數方差明顯高于試驗實測值，說明試驗模型上的脈動風偏角并非高斯過程。就本次試驗結果而言，風偏角的線性假設比高斯假設更接近實測值，這是一個有趣的現象，但該現象有無普遍性和代表性，還有待更深入更廣泛的研究。

圖5　紊流場中氣動力系數的概率密度( =9.56 m/s) Fig.5 Probability densities of aerodynamic coefficients in turbulent flow( =9.56 m/s)

圖6　紊流場中氣動力系數的自功率譜密度( =9.56 m/s) Fig.6 Power spectrum densities of aerodynamic coefficients in turbulent flow( =9.56 m/s)

3頻域氣動導納函數

3.1導納函數定義

導納函數可由脈動風力功率譜SLi和來流脈動風速功率譜Sui的比值直接計算氣動導納。

根據定義，氣動導納函數也可以用式(11)計算[2]:

(11a)

(11b)

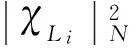
3.2導納函數擬合方法

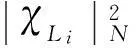
(12)

3.3氣動導納函數識別與討論

根據式(11)和式(12)，得到的平滑后的導納測量結果及其擬合結果見圖7(a)～(b)，擬合參數a、b、c的結果列于表2中，為研究方便起見，取不同風向角下阻力或升力氣動導納擬合曲線的均值為其名義導納函數，該名義導納函數雖不能代表每一個工況的實際情況，但是卻可以簡明地反映出試驗輸電塔模型氣動導納的整體特征。

通過對比不同風向角時導納函數擬合曲線發現，各曲線的變化趨勢相似。阻力導納函數有隨折減頻率的增大而遞減，升力導納函數在低頻段隨折減頻率增大而增大，在高頻段隨之增大而減小。氣動導納函數對風向角敏感，隨角度變化沒有很明顯的規律。

圖7(c)為線性導納和非線性導納的對比。從圖中可見，阻力和升力的非線性導納函數為小于1.0的變量，其最大值分別約為0.95和0.1。也就是說對于此類輸電塔，考慮氣動導納后的抖振響應比不考慮時低。在k<0.27時阻力導納值大于升力導納值，在k>0.27時升力導納值大于阻力導納值，說明高頻率的脈動風分量對升力的影響較對阻力的影響更明顯。線性導納函數明顯小于相應的非線性導納函數，線性阻力和升力導納的最大值分別為0.07和0.01，比非線性導納函數小了一個數量級，脈動風和結構抖振力之間有明顯的非線性傳遞關系，原因不外乎以下四點：一是在較高紊流度時忽略脈動風高階成分有較大的偏差；二是抖振力并不完全依賴于脈動風速，比如還與空間尺度有關；三是總導納函數還包括了含結構阻尼和氣動阻尼在內的所有阻尼效應的影響；四是測量和分析時存在系統誤差。此外，經過與8m/s和12m/s風速下的氣動導納測量結果對比發現，風速對氣動導納值的影響不明顯。

圖8給出了抖振力功率譜測量值和相應的根據線性導納計算的抖振力譜，線性抖振力功率譜明顯低于試驗測得的抖振力譜，再次說明湍流風場中抖振力與風的脈動分量間關系復雜，不能簡單地用線性輸出力譜和風譜的比值來確定桁架式輸電塔架的導納函數。

圖7　各風向角下阻力(a)和升力(b)非線性總氣動導納函數擬合，以及線性和非線性導納函數對比(c) Fig.7 Fitted admittance functions of drag (a) and lift (b) force, and comparison of linear and nonlinear admittance functions (c)

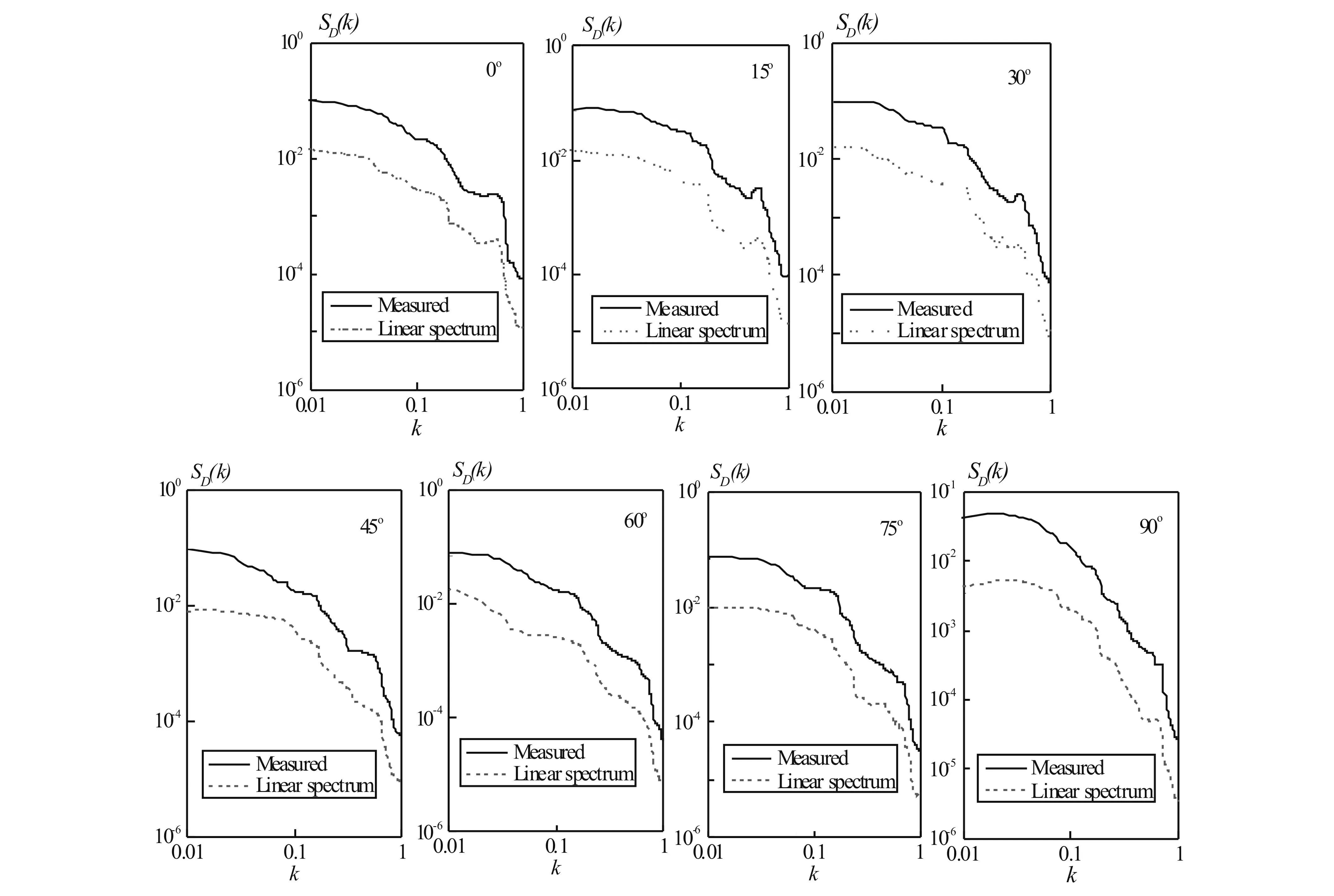
Fig.8　實測抖振力譜及相應的線性譜 Fig.8 Comparison of measured buffeting force spectra with corresponding linear spectra

表2　氣動導納參數擬合結果

4結論

通過高頻天平測力試驗，對細高格構式特高壓輸電塔架的氣動力系數進行了測量與研究。結果表明對輸電塔來說，沿其主軸方向(X、Y向)的最大力由和該主軸呈15°角的風產生，而非沿主軸方向的風產生。

氣動力系數和脈動風偏角之間為弱非線性，本次試驗結果表明，輸電塔模型風偏角φ′并不接近高斯分布。但無論用哪種方法，橫向湍流引起的抖振升力效應都不可忽略。就基底抖振力來看，對于紊流場中的格構式輸電塔架來說，雷諾數的影響已很小，可以不予考慮。

提出了考慮結構氣動阻尼力的總體氣動導納概念，通過對模型基底抖振力和來流脈動風速功率譜的測量，采用直接法對格式式輸電塔架的氣動導納函數在頻域內進行了識別。結果表明，線性導納函數計算的抖振力譜會大大低估脈動風分量的影響，不考慮導納函數將會高估結構的動力響應。本文還給出了橫向升力導納函數的識別結果，可用于輸電塔橫向振動的時程計算。

參考文獻

[1]Peil U, Behrens M. Dynamic response of slender structures under wind load[A]. In: Grundmann H, Schu?ller G I. Proceeding of the fifth European Conference on Structural Dynamics[C]. Munich, Germany: Taylor & Francis, 2002: 141-152.

[2]Peil U, Behrens M. Aerodynamic admittance models for buffeting excitation of high and slender structures[J]. J. Wind Eng. Ind. Aerodyn., 2007, 95: 73-79.

[3]Walshe D E, Wyatt T A. Measurement and application of the aerodynamic admittance function for a box-girder bridge[J]. J. Wind Eng. Ind. Aerodyn., 1983, 14: 211-222.

[4]Jakobsen J B. Fluctuating wind load and response of a line-like engineering structure with emphasis on motion-induced wind forces[D]. Trondheim, Norway: Department of Structural Engineering, University of Trondheim, 1995.

[5]Snaker P P, Jones N P, Scanlan R H. Identification of aeroelastic parameters of flexible bridges[J]. ASCE Journal of Engineering Mechanics, 1994, 120(8): 1718-1741.

[6]趙林, 葛耀君, 李鵬飛. 氣動導納函數互譜識別法注記[A]. 第十三屆全國結構風工程學術會議論文集[C]. 大連: 2007:698-707.

[7]李正良, 肖正直, 韓楓,等. 1000kV漢江大跨越特高壓輸電塔線體系氣動彈性模型的設計與風洞試驗[J]. 電網技術, 2008, 32(12): 1-5.

LI Zheng-liang, XIAO Zheng-zhi, HAN Feng, et al. Aeroelastic model design and wind tunnel tests of 1000kV Hanjiang long span transmission line system[J]. Journal of Power System Technology, 2008, 32(12):1-5.

[8]鄧洪洲, 司瑞娟, 胡曉依,等. 特高壓輸電塔氣彈模型風洞試驗研究[J]. 同濟大學學報(自然科學版), 2010, 38(5): 673-678.

DENG Hong-zhou, SI Rui-jian, HU Xiao-yi, et al. Wind tunnel test on aeroelastic model of UHV latticed transmission tower[J]. Journal of Tongji University(Natural Science), 2010, 38(5): 673-678.

[9]樓文娟, 孫炳楠, 唐錦春. 高聳格構式結構風振數值分析及風洞試驗[J].振動工程學報, 1996, 9(3): 318-322.

LOU Wen-juan, SUN Bing-nan, TANG Jin-chun. Wind tunnel test and numerical computation on wind-induced vibration for tall lattice tower[J]. Journal of Vibration Engineering, 1996, 9(3): 318-322.

[10]中華人民共和國住房和城鄉建設部. GB50009-2012 建筑結構荷載規范[S]. 北京: 中國建筑工業出版社, 2012.

[11]International Standard Organization. ISO 4354: 2009(E) Wind Actions on Structures[S]. Geneva: International Standard Organization, 2009.

[12]鄒良浩, 梁樞果. 半剛性模型風洞試驗荷載譜的處理方法[J]. 實驗流體力學, 2007, 21(3): 76-81.

ZOU Liang-hao, LANG Shu-guo. A method to evaluate wind force spectra of semi-rigid model in wind tunnel tests[J]. Journal of Experiments in Fluid Mechanics, 2007, 21(3): 76-81.

[13]程志軍, 付國宏, 樓文娟等. 高聳格構式塔架風荷載試驗研究[J]. 試驗力學, 2000, 15(1): 51-55.

CHENG Zhi-jun, FU Guo-hong, LOU Wen-juan, et al. Research for the wind force on high-rise latticed tower[J]. Journal of Experimental Mechanics, 2000, 15(1): 51-55.

[14]Bendat J S, Piersol A G. Random data-analysis and measurement procedures(4thEdition)[M]. New York: Wiley, 2010:180-190.

[15]Davenport A G. Buffeting of a suspension bridge by storm winds[J]. J. Struct. Engrg. Div. ASCE, 1962, 88(6): 233-264. U, Behrens M. Dynamic response of slender structures under wind load[A]. In: Grundmann H, Schu?ller G I. Proceeding of the fifth European Conference on Structural Dynamics[C]. Munich, Germany: Taylor & Francis, 2002: 141-152.

[2]Peil U, Behrens M. Aerodynamic admittance models for buffeting excitation of high and slender structures[J]. J. Wind Eng. Ind. Aerodyn., 2007, 95: 73-79.

[3]Walshe D E, Wyatt T A. Measurement and application of the aerodynamic admittance function for a box-girder bridge[J]. J. Wind Eng. Ind. Aerodyn., 1983, 14: 211-222.

[4]Jakobsen J B. Fluctuating wind load and response of a line-like engineering structure with emphasis on motion-induced wind forces[D]. Trondheim, Norway: Department of Structural Engineering, University of Trondheim, 1995.

[5]Snaker P P, Jones N P, Scanlan R H. Identification of aeroelastic parameters of flexible bridges[J]. ASCE Journal of Engineering Mechanics, 1994, 120(8): 1718-1741.

[6]趙林, 葛耀君, 李鵬飛. 氣動導納函數互譜識別法注記[A]. 第十三屆全國結構風工程學術會議論文集[C]. 大連: 2007:698-707.

[7]李正良, 肖正直, 韓楓,等. 1000kV漢江大跨越特高壓輸電塔線體系氣動彈性模型的設計與風洞試驗[J]. 電網技術, 2008, 32(12): 1-5.

LI Zheng-liang, XIAO Zheng-zhi, HAN Feng, et al. Aeroelastic model design and wind tunnel tests of 1000kV Hanjiang long span transmission line system[J]. Journal of Power System Technology, 2008, 32(12):1-5.

[8]鄧洪洲, 司瑞娟, 胡曉依,等. 特高壓輸電塔氣彈模型風洞試驗研究[J]. 同濟大學學報(自然科學版), 2010, 38(5): 673-678.

DENG Hong-zhou, SI Rui-jian, HU Xiao-yi, et al. Wind tunnel test on aeroelastic model of UHV latticed transmission tower[J]. Journal of Tongji University(Natural Science), 2010, 38(5): 673-678.

[9]樓文娟, 孫炳楠, 唐錦春. 高聳格構式結構風振數值分析及風洞試驗[J].振動工程學報, 1996, 9(3): 318-322.

LOU Wen-juan, SUN Bing-nan, TANG Jin-chun. Wind tunnel test and numerical computation on wind-induced vibration for tall lattice tower[J]. Journal of Vibration Engineering, 1996, 9(3): 318-322.

[10]中華人民共和國住房和城鄉建設部. GB50009-2012 建筑結構荷載規范[S]. 北京: 中國建筑工業出版社, 2012.

[11]International Standard Organization. ISO 4354: 2009(E) Wind Actions on Structures[S]. Geneva: International Standard Organization, 2009.

[12]鄒良浩, 梁樞果. 半剛性模型風洞試驗荷載譜的處理方法[J]. 實驗流體力學, 2007, 21(3): 76-81.

ZOU Liang-hao, LANG Shu-guo. A method to evaluate wind force spectra of semi-rigid model in wind tunnel tests[J]. Journal of Experiments in Fluid Mechanics, 2007, 21(3): 76-81.

[13]程志軍, 付國宏, 樓文娟等. 高聳格構式塔架風荷載試驗研究[J]. 試驗力學, 2000, 15(1): 51-55.

CHENG Zhi-jun, FU Guo-hong, LOU Wen-juan, et al. Research for the wind force on high-rise latticed tower[J]. Journal of Experimental Mechanics, 2000, 15(1): 51-55.

[14]Bendat J S, Piersol A G. Random data-analysis and measurement procedures(4thEdition)[M]. New York: Wiley, 2010:180-190.

[15]Davenport A G. Buffeting of a suspension bridge by storm winds[J]. J. Struct. Engrg. Div. ASCE, 1962, 88(6): 233-264.