基于汽車座椅導軌試驗模態的結合部剛度優化

張 晨，余慧杰，丁曉紅

（上海理工大學 機械工程學院，上海 200093）

0 引言

研究表明，振動問題60%來自結合部［1］，雖然結合部對整機動態特性影響巨大，但是由于結合作用機理相當復雜，其參數往往無法準確識別。隨著有限元技術的發展，仿真分析已成為研究動態特性問題的新方法，但是結合部建模的準確性亦成為阻礙仿真技術發展的瓶頸。因此，對結合部有限元建模方法的研究自然成為一個重要的課題與研究方向。

汽車座椅導軌是座椅與車身之間的連接件，在汽車行駛過程中若導軌產生明顯異響將使乘客對整車質量留下糟糕的印象。在對座椅各主要連接部件分析的基礎上，可以確定導軌內部鋼珠與內外軌之間結合部的動態特性是振動噪聲的主要來源。由于鋼珠位置處于導軌內部，難以通過試驗方式獲取結合部參數，因此在仿真建模時無法給出結合部參數。為此，本文以汽車座椅導軌為例，闡述一般有限元模型結合部建模時快速獲取接觸剛度的方法。該方法將模態試驗技術和有限元方法相結合，并運用優化方法對結合部參數進行反推。

1 結合部建模及接觸剛度理論計算方法

目前對于結合部的建模方法，若簡化處理則有剛性連接與接觸對；較為準確的模擬方法則有等參數接觸單元與彈簧－阻尼單元［2］。其中，剛性連接完全不考慮接觸部位的動態特性，只適用于整體的宏觀研究；接觸對模擬則以摩擦因數表征接觸關系，但對每種接觸形式無法給出合適的摩擦因數；等參數接觸單元通過單元節點的相對位移推導出單元剛度矩陣，但該方法不考慮各節點之間的耦合作用，目前只在整機的仿真計算中進行驗證；彈簧－阻尼單元以剛度和阻尼來表征結合部的動態特性，但是剛度和阻尼難以準確獲取，阻礙了該方法的廣泛應用。

本文介紹的方法不同之處在于通過有限元優化技術快速反推結合部參數，以彌補傳統彈簧－阻尼建模方法的不足。一般而言阻尼對系統的固有頻率與振型影響較小，所以本文所述方法中不對接觸阻尼進行優化，建模時所需的阻尼參數由模態試驗中測得的模態阻尼比來代替。目前接觸剛度的識別多采用動態特性試驗法或理論計算法。動態特性試驗法對結合部結構依賴較高，不適用于裝配不便的結構，因此該方法的使用受到很大的限制。而理論計算法，接觸剛度kN可以由作用在彈性體上的法向壓力F除以法向趨近量δN獲得，即：

根據赫茲接觸理論，彈性力學中給出了兩個彈性體之間的法向趨近量的計算公式［3］：

圖1為汽車座椅導軌切面垂向受力示意圖。其中，各鋼珠所受彈性力分別為F1、F2、F3、F4，α＝45°，Fz為通過座椅傳遞至導軌的垂向外載荷。對于內軌，根據靜力平衡條件有：

其中：z為單列滾道內鋼珠數量。

圖1 導軌垂向受力示意圖

類比接觸軸承的支承剛度計算方法［5］，在Fz的作用下，鋼珠A的彈性趨近量應等于鋼珠B的彈性恢復量，并且彈性體在某一方向上的總變形應該等于各分力作用在該方向的變形之和。另外由赫茲接觸理論可知，彈性體的法向趨近量正比于其法向作用力的2/3次方，即：

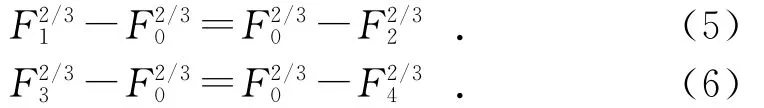
其中：F0為預載荷下單個鋼珠所受的法向力。

在z、α、Fz、F0都為已知量時，根據式（3）～式（6）可以求出單個鋼珠所受的法向壓力。當求得各法向力之后可以根據公式（1）求得接觸剛度kN。

直線滾子導軌橫向與切向受力的剛度計算方法與垂向類似，這里不再贅述。通過以上的計算方法，即可建立直線滾子導軌結合部動態特性參數模型。由此可見，理論計算方法過程繁瑣，且受赫茲接觸理論假設的約束，未考慮接觸相對滑移等問題，因此理論計算法無法滿足結合部建模的通用性、快速性需求。

2 座椅導軌實物模態試驗

試驗模態分析主要基于線性振動理論，通過試驗將采集的系統輸入與輸出信號經過參數識別獲得模態參數。本次測試中采用DH5927動態測試分析系統，試驗中將導軌用軟繩懸掛起來近似模擬自由狀態，用錘擊法按照激勵點移動、響應點固定的方式來測試傳遞函數。

由振動力學可知，在結構的振動過程中引起振動的主要因素是低階模態，并且由于實際結構中阻尼的存在，較高階模態的振型將迅速衰減。另外，導軌對路面激勵敏感頻率為40Hz以下的低頻段，故我們找到前2階模態固有頻率及振型，并以此作為剛度優化中的優化目標值。若需對更多階模態進行研究，方法相同。表1為試驗模態固有頻率及阻尼比，圖2為試驗模態振型圖。

表1 試驗模態固有頻率及阻尼比

3 座椅導軌有限元模型

本次FEA模型的建立是基于Altair公司的HyperMesh軟件進行的。在HyperMesh中用殼單元對薄壁件進行數學離散。在該模型中，外軌長450mm，內軌長402mm，采用基本尺寸為5mm×5mm的CQUAD4單元，并賦予殼單元實際部件的厚度。模型中共有節點7 913個、單元7 406個，選取各向同性材料建立材料模型，其中彈性模量E為210GPa，泊松比為0.3，密度為7 900kg/m3。汽車座椅導軌有限元模型如圖3所示。

圖2 試驗模態振型

導軌內部鋼珠的模擬是本次建模的關鍵，為簡化問題，我們將鋼珠視為剛體。建模過程中在24個鋼珠位置嵌入彈簧單元（CBUSH單元），每個鋼珠由一個CBUSH單元（CBUSH單元兩端點位置重合）和兩個RBE2單元（剛性單元）構成。根據彈簧單元位置的對稱性，將其分成4組。彈簧單元可賦予6個自由度（3個軸向線位移自由度，3個旋轉角自由度）方向剛度。需要注意的是CBUSH單元需要賦予一個局部坐標系，其6個自由度方向也是相對于局部坐標系而言的。

圖3 汽車座椅導軌有限元模型

4 基于試驗模態的剛度優化

在HyperWorks中的OptiStruct模板下用Lanczos法按質量矩陣歸一化對導軌模型進行自由模態實特征值提取。初始分析中為彈簧給定一組初始剛度值。在剛度給定過程中，發現4組彈簧旋轉角自由度方向剛度對計算模態結果無影響，故只考慮4組彈簧12個軸向線位移剛度。當12個剛度都指定為500N/m時，除去前6階剛體模態之后，導軌系統前2階模態固有頻率如表2所示。

表2 給定初值計算所得模態固有頻率值

初始分析完成之后，在OptiStruct模板下進行尺寸優化。以試驗模態1、2階固有頻率為目標，彈簧單元剛度值為設計變量，運用最小二乘法進行剛度優化。

4.1 設計變量

設計變量為要優化的結合部接觸剛度，即4組彈簧的各方向剛度Kx、Ky、Kz，共12個設計變量。給定500 N/m為初始值，設定設計變量的變化范圍在1N/m～1 000N/m。

4.2 設計目標

用最小二乘法最小化如下目標函數：

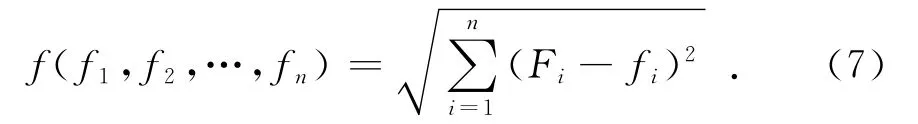
其中：Fi、fi分別為試驗與計算模態第i階固有頻率。

4.3 優化結果分析

優化后目標函數最小二乘偏差為2.59×10－5Hz，優化后的固有頻率計算結果見表3，優化計算得到的彈簧剛度見表4。

表3 優化后的導軌模態固有頻率值

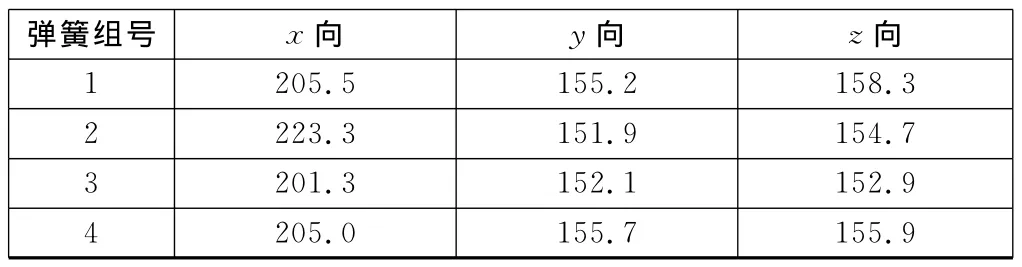
表4 優化后彈簧剛度N/m

優化后的第1、2階模態振型與試驗模態振型對比如圖4所示。

經過對比，優化后導軌系統模態振型與試驗模態對應階次的振型相吻合，所以我們認為在此過程中所得優化后的彈簧剛度即為所要得到的結合部等效接觸剛度。

5 結束語

通過模態試驗技術與有限元模態分析相結合的方法，對汽車座椅導軌結合部接觸剛度進行了優化，得到了該導軌各階固有頻率及振型。通過對比研究，說明該模型的參數優化結果是可取的，模型的建立是成功的。該研究結果表明，基于實測參數的有限元優化方法能夠較好地解決結合部等效參數獲取問題，從而為一般結合部建模提供了解決方案。

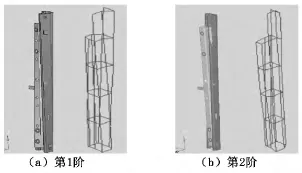
圖4 優化后模態振型與試驗模態振型對比

［1］郭鐵能，李玲，蔡力鋼，等.基于頻響函數辨識機械結合部動態參數的研究［J］.振動與沖擊，2011，30（5）：69-72.

［2］王世軍，黃玉美，趙金娟，等.機床導軌結合部的有限元模型［J］.中國機械工程，2004，15（18）：1634-1636.

［3］王槐，代霜.大接觸角推力球軸承接觸的有限元仿真研究［J］.計算機仿真，2013，30（1）：308-309.

［4］程光仁，施祖康，張超鵬，等.滾珠螺旋傳動設計基礎［M］.北京：機械工業出版社，1987.

［5］蔣書運，祝書龍.帶滾珠絲杠副的直線導軌結合部動態剛度特性［J］.機械工程學報，2010，46（1）：92-99.