低速重載下齒根彎曲強度有限元分析

張金泉

（鎮江市江南礦山機電設備有限公司，江蘇 鎮江 212009）

0 引言

鎮江市江南礦山機電設備公司自行研制的新型節能型起重永磁鐵采用齒輪齒條傳動，其中齒條帶動直齒圓柱齒輪，直齒圓柱齒輪與轉軸軸頸采用普通平鍵連接，從而實現轉軸的轉動，轉軸的驅動轉矩約為3 000Nm。起重永磁鐵頻繁地吸放鋼板，轉軸需要作間歇性的正反轉來完成，且轉軸轉速很低，約3r/min。針對這種低速重載的工況，齒輪齒條的主要失效形式為輪齒折斷。國內對齒輪齒根彎曲應力問題開展了較多的研究，如武漢理工大學的黃海等［1］對點線嚙合齒輪齒根彎曲應力進行研究，并修正了齒輪的齒根彎曲應力計算公式；南京航空航天大學的靳廣虎［2］對圓柱齒輪進行了有限元分析，研究了在齒頂受載時輪齒的應力分布規律；北京科技大學的李寧等［3］對對稱與非對稱齒輪齒根彎曲應力進行了ANSYS有限元分析，研究表明在相同參數條件下，非對稱齒輪在正反轉過程中，其齒根彎曲強度優于對稱標準齒輪；吉林大學的趙強［4］針對汽車傳動系統中的變速器斜齒輪，使用ANSYS的參數化語言APDL完成了齒根彎曲應力的有限元分析。本文在結合前人研究的基礎上，考慮到低速重載下齒輪齒條嚙合的特殊性，選取嚙合過程中的不同嚙合時刻（嚙合位置）對齒輪的齒根彎曲強度進行分析，從而獲得了嚙合過程中的齒根彎曲應力及輪齒齒廓的變形值，對齒輪機構的設計與校核具有一定的指導意義。

1 齒輪有限元模型

起重永磁鐵采用齒輪齒條機構傳動，標準直齒圓柱齒輪與標準齒條嚙合時重合度為1.981。為便于對嚙合過程中的齒輪進行有限元分析，特采取以下的假設：①在計算時，齒輪齒條嚙合時的重合度取為2，即在任意時刻認為齒輪與齒條都有兩對齒參與嚙合；②在進行有限元分析時，輪齒所受載荷為均布載荷，且兩齒所受載荷大小相等。

齒輪參數見表1，齒輪齒條的三維模型如圖1所示。采用三維繪圖軟件SolidWorks進行建模。為便于ANSYS的求解分析，特簡化模型，選取嚙合過程的3齒來計算，其有限元模型如圖2所示。

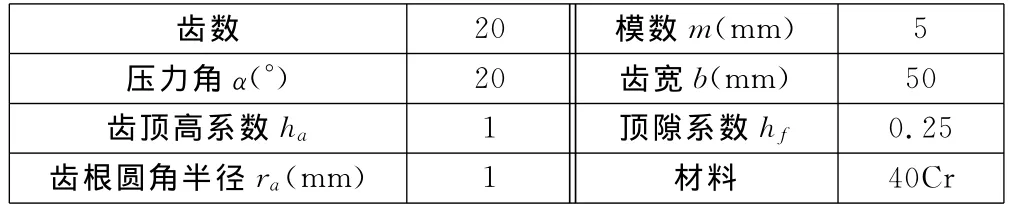
表1 齒輪參數

2 齒根彎曲強度的仿真及結果分析

采用有限元分析軟件ANSYS對齒輪的齒根彎曲應力及變形值進行求解。選取單元類型為SOLID187，齒輪材料的彈性模量為E＝206 000N/mm2，泊松比為0.28，許用彎曲應力［σF］＝297MPa。為了便于分析嚙合過程中輪齒的彎曲應力和變形值，對3齒進行編號（見圖2）。選取齒輪齒條嚙合過程中的8個時刻，首先從齒輪的1號齒、2號齒參與齒條的嚙合過程中選取4個時刻，假定在初始時刻，齒條的一齒齒頂與1號齒的齒根部位嚙合，則齒條的相鄰齒齒根與2號齒的齒頂嚙合，直至1號齒即將脫離嚙合；其次從齒輪的2號齒、3號齒參與齒條的嚙合過程中選取后4個時刻，即齒條的一齒齒頂與2號齒的齒根部位嚙合，則齒條的相鄰齒齒根與3號齒的齒頂嚙合，直至2號齒即將脫離嚙合。對嚙合過程中的8個時刻分別進行求解，進而獲得齒輪的齒根彎曲應力與齒形的變形量隨嚙合過程的變化情況。

圖3為嚙合初始時刻（時刻1）齒輪的齒根彎曲應力分布及齒形變形情況。由于齒輪的1號齒與2號齒參與嚙合，齒根彎曲應力在1號、2號齒的齒根部位較大，其中2號齒的齒根彎曲應力最大，約為229MPa；變形量較大部位在1號、2號齒的齒頂，其中2號齒的齒頂變形量最大，為15.9μm。

圖1 齒輪齒條三維模型

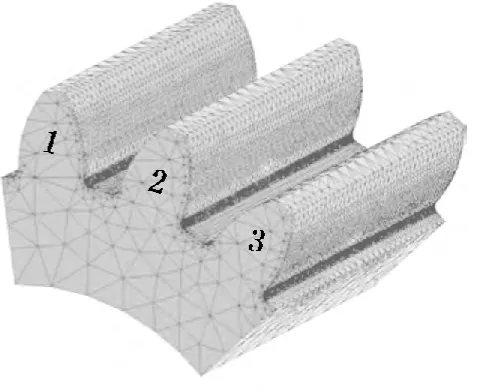
圖2 齒輪有限元網格劃分圖（3齒）

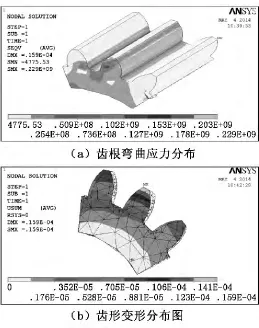
圖3 嚙合初始時刻齒輪齒根彎曲應力與變形情況

圖4為嚙合過程中8個時刻的最大齒根彎曲應力曲線。前4個時刻為1號、2號齒參與嚙合的過程，3號齒未參與嚙合，因此3號齒齒根彎曲應力為零。后4個時刻為2號、3號齒參與嚙合的過程，1號齒已經脫離嚙合，因此1號齒的齒根彎曲應力為零。從3個齒的整個嚙合過程來看，1號齒的齒根彎曲應力逐漸增大，然后減小為零；2號齒的齒根彎曲應力先減小后增大，基本按照拋物線規律變化；3號齒的齒根彎曲應力由零變最大，然后逐漸減小。嚙合過程中，最大的齒根彎曲應力約為250MPa，此值雖小于齒輪材料的許用彎曲應力，不會出現輪齒的折斷，但是輪齒在此循環交變應力的作用下會出現疲勞破壞，這是需要注意的。

圖5為齒輪齒條嚙合過程中8個時刻的齒形最大變形曲線。其中2號齒表示了齒輪的一個齒從嚙合開始時刻至嚙合終了時刻的齒廓變形情況。由圖5可以看出，輪齒在嚙合過程中，齒廓的變形量具有類似拋物線的變化規律，齒廓的最大變形量約為17μm，可見在低速重載下齒廓的變形量較大。

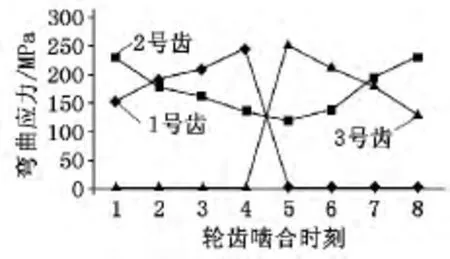
圖4 嚙合過程中8個時刻的最大齒根彎曲應力曲線

圖5 嚙合過程中8個時刻的最大齒形變形曲線

3 結論

通過ANSYS軟件對低速重載下的齒輪3齒模型進行了有限元仿真分析，獲得了嚙合過程中的齒根彎曲應力值與齒廓變形值。仿真結果可以看出，嚙合過程中齒根彎曲應力值與齒廓變形值基本呈拋物線規律變化，雖然最大齒根彎曲應力并未超出材料的許用應力值，但是齒輪輪齒在一定次數的循環交變應力作用下會出現疲勞破壞。

［1］黃海，厲海祥，羅齊漢，等.點線嚙合齒輪齒根彎曲應力研究［J］.機械傳動，2011，35（1）：8-11.

［2］靳廣虎.正交面齒輪傳動的強度與動力學特性分析研究［D］.南京：南京航空航天大學，2012：45-52.

［3］李寧，李威，肖望強.對稱與非對稱齒輪齒根彎曲應力對比分析［J］.北京科技大學學報，2013，35（1）：120-124.

［4］趙強.變速器齒輪彎曲應力分析建模與仿真［D］.長春：吉林大學，2009：61-64.