變徑管與薄壁圓管軸向壓縮過程研究

徐龍江，雷君相，高貴杰

（上海理工大學 材料成形與模具研究所，上海 200093）

0 引言

變徑管作為一種有效吸能元件［1］受到廣泛關注，國內外對其研究也越來越多［2］。變徑管在受軸向壓縮時，其內管和外管都受到力的作用［3］，各部分的變形模式有很多種，如自由翻轉、內管和外管的軸對稱或非軸對稱失穩［4］等。為了能直觀地研究變徑管在軸向載荷作用下的變形過程，將變徑管的內管、中管和外管抽象出來單獨研究，其中內管和外管可以看作只受軸向壓縮，中管受軸向拉伸。結合圓管軸向壓縮，可以對變徑管的變形過程作系統研究，從而為變徑管在軸向壓縮過程中出現自由翻轉提供新的理論依據。

1 理論研究

變徑管結構及軸向壓縮過程如圖1所示，在軸向載荷作用下，其內管和外管受到軸向壓縮，中管受軸向拉神［5］。根據應力應變曲線，斷裂強度大于屈服強度，因此中管拉斷時的力應該遠大于壓縮內管和外管時的壓力。因此本文研究的重點是薄壁圓管壓縮和變徑管自由翻轉。變徑管幾何尺寸如表1所示。

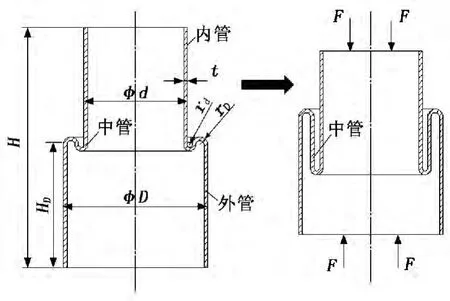
圖1 變徑管結構及軸向壓縮過程

1.1 薄壁圓管軸向壓縮載荷

當薄壁圓管受軸向壓縮時，其塑性破損模式可能是軸對稱或非軸對稱形式，這主要取決于圓管外徑和厚度之比（D0/t）。軸對稱模式通常稱為圓環模式，而非軸對稱模式被稱為鉆石模式。一般而言，D0/t＞80的圓管發生鉆石模式的破損，D0/t＜50時發生圓環模式的破損［6］。圖1所示的變徑管中，內管和外管的直徑與厚度之比均小于50，在軸壓下均發生圓環模式的破損。

表1 變徑管幾何尺寸

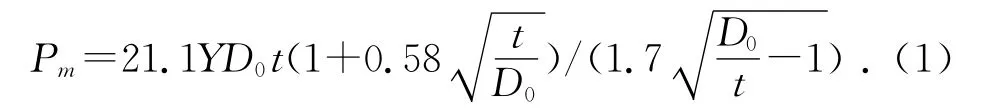
其中：Y為屈服應力。

金屬薄壁圓管采用20鋼，將Y＝296MPa、D0＝40mm、t＝1.4mm 代入式（1）中，得出壓縮內管的平均載荷為47.9kN；當Do＝56mm時，得出壓縮外管的平均載荷為54.7kN。

1.2 變徑管軸向壓縮載荷

變徑管在軸向壓縮作用下發生自由翻轉，在自由翻轉的穩定階段，自由翻轉力將達到最高值且保持不變［7］。由上海理工大學雷君相教授推導的變徑管自由翻轉吸能元件內管外翻的翻轉力公式為：

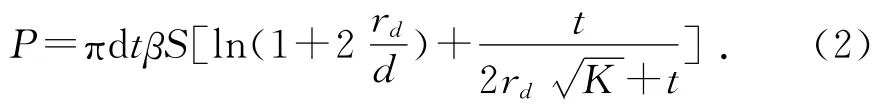
對于受軸向壓縮的薄壁圓管而言，一般采用的理論模型是Alexander模型，即通過塑性鉸來建立平衡方程，進行圓管軸對稱壓潰分析，得到完成整個褶皺過程的平均載荷Pm：

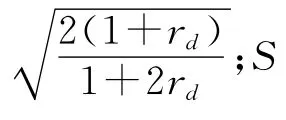
2 模擬研究

本文模擬采用薄壁圓管，其彈性模量為210GPa，泊松比為0.3，密度為7 800kg/m3。由于此次壓縮模擬的位移較大，接觸較復雜，故模擬實驗采用ABAQUS/Explicit軟件進行有限元分析，模型中圓管和變徑管采用三維的可變形體，上、下壓頭均采用解析剛體，材料屬性中輸入圓管彈性參數和塑性參數，摩擦因數設為0.1。壓縮圓管時要設置圓管的自接觸，防止圓管發生穿透現象，使模擬結果更加真實。圖2為所要壓縮的薄壁金屬圓管和變徑管的有限元模型。

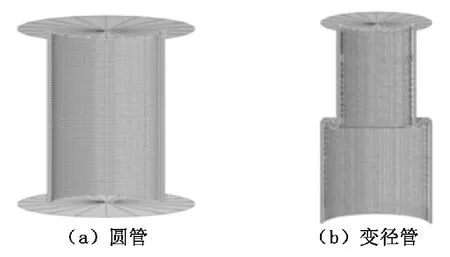
圖2 圓管和變徑管的有限元模型

為了比較壓縮后的結果，設置壓縮的位移量s＝30mm，薄壁金屬管和變徑管壓縮的模擬結果如圖3所示。

圖3 圓管和變徑管的壓縮結果

從壓縮結果可以看出：圓管受壓縮發生軸對稱失穩，其失穩模式為圓環模式，產生較為規則的褶皺；變徑管經壓縮后，內管和外管變形為中管，中管逐漸由短變長，整個過程比較穩定。

3 結果分析

圓管內管、圓管外管和變徑管3種壓縮過程的載荷－位移曲線如圖4所示。從圖4中可以看出，圓管內管和外管發生軸對稱失穩時，載荷先達到一個最大的初始峰值，隨后急劇下降，然后波動起伏，這些波動是由連續褶皺產生的，每一個峰值對應于一個褶皺過程的開始。

變徑管自由翻轉開始階段，載荷隨著加載位移的增加而增大，達到一個峰值，之后出現下降，最后會達到一個穩定值并持續進行下去。變徑管自由翻轉的載荷－位移曲線比較平穩，與模擬出現的中管平直穩定這一結果相吻合。并且變徑管的載荷－位移曲線和圓管的載荷－位移曲線相比，多處于其下方，表明變徑管翻轉穩定時的載荷要小于壓縮圓管時的載荷。

由于壓縮圓管產生的載荷最大峰值遠大于變徑管自由翻轉時產生的載荷最大峰值，因此，變徑管在發生軸向壓縮時更易發生自由翻轉，而不會發生內管或者外管的軸對稱失穩；根據載荷的平穩程度，變徑管的自由翻轉是理想的變形模式，可以作為吸能元件應用于各種碰撞場合。

表2為圓管壓縮和變徑管自由翻轉的理論計算值和模擬結果對比。由表2可以看出，理論計算出的變徑管自由翻轉時的平均載荷和模擬結果基本吻合，模擬結果中自由翻轉下的Pm是自由翻轉過程中載荷穩定狀態時的力。

圖4 圓管和變徑管軸向壓縮的載荷－位移曲線

表2 圓管壓縮和變徑管自由翻轉的理論計算和模擬結果對比

4 結論

（1）薄壁圓管壓縮時的最大載荷遠大于變徑管自由翻轉時的最大載荷。

（2）軸向壓縮時，薄壁圓管發生軸對稱失穩，變徑管發生自由翻轉，不會發生內管或者外管的軸對稱失穩。

（3）變徑管在發生自由翻轉時的變形模式穩定，載荷隨加載位移的增加保持恒定，可以作為理想的吸能元件。

（4）理論計算出的變徑管自由翻轉時的平均載荷和模擬結果基本吻合。

［1］Guillow S R，Lu G，Grzebieta R H.Quasi static axial compression of thin－walled circular aluminum tubes［J］.International Journal of Mechanical Science，2001，43：2103－2123.

［2］張立玲，高峰，杜發榮.不等厚拼焊管軸向壓縮變形的數值模擬研究［J］.塑性工程學報，2006，13（4）：6－19.

［3］劉德學，何清和，袁文輝，等.薄壁圓管變形吸能元件準靜態壓潰吸能分析［J］.電力機車與城軌車輛，2011，34（3）：37－39.

［4］張立玲，林逸，高峰.不同材料薄壁圓管準靜態軸壓變形特性［J］.塑性工程學報，2010，17（4）：62－65.

［5］雷君相，李笠.圓管縮徑能量吸收裝置的研究［J］.塑性工程學報，1995，2（2）：57－64.

［6］余同希，盧國興.材料與結構的能量吸收［M］.北京：化學工業出版社，2006.

［7］王敏杰，雷君相.變徑管自由翻轉過程研究［J］.熱加工工藝，2013，42（5）：146－148.