方程應用題的教學之我見
田磊
【中圖分類號】G633.6 【文獻標識碼】A 【文章編號】2095-3089(2015)12-0118-01
遵循題型教授方程應用題,把表面復雜的應用題歸納為行程問題、工程問題、效率問題、分配問題、利潤問題、和差倍分等幾類題型,再把每類題型都進行細致入微的講解,就好像給了學生一個模板,當學生遇到應用題時,先看它們屬于哪一種題型,然后再對照模板,運用相應的方法解決。這樣做確實可以幫助學生理清思路,得以較快的解決問題。在實際教學中,絕大多數的老師都或多或少的使用了這種方法。這也充分說明了遵循題型教授方程應用題,在某種程度上是比較有效果的。
但是,任何事物的產生都具有兩面性,遵循題型教授方程應用題在學習應用題之初具有其向導作用,但是從長久來說,它又束縛了學生的思維,學習用方程解應用題的主要目的是培養學生分析和解決實際問題的能力,而生活中的問題又豈是幾種類型所能概括的,遵循題型教授方程應用題,僅能使學生牢牢的掌握幾種類型題目的解法,對于不好劃分類型的應用問題便無從下手。長此以往,不利于學生發散性思維的訓練和培養。
應用題之所以難,主要是很難理清實際問題中復雜的數量關系,從而列不出方程。因此對應用題的教學,應當把重點放在讓學生如何把未知轉化為已知,如何去發現等量關系上,而不應過分的看重題型。
在初中階段,列代數式,方程、方程組的應用,不等式、不等式組的應用,函數的應用等,基本涵蓋了初中代數知識的所有應用,我都采取了同樣的分析方法:①畫線段示意圖;②列表格。
畫線段示意圖主要適用于行程問題,現舉例如下:
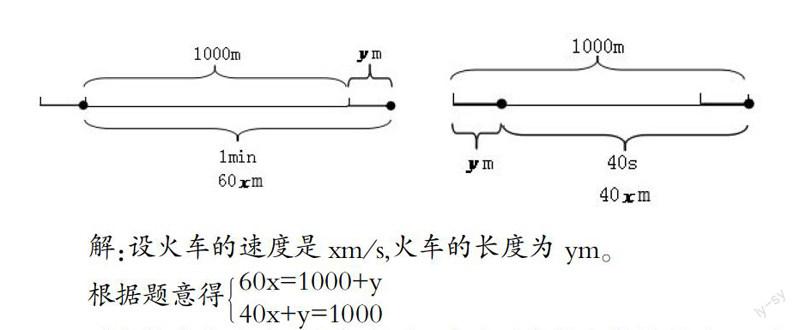
例1:某鐵路橋長1000m, 現有一列火車從橋上通過,測得該火車從開始上橋到完全過橋共用了1min , 整列火車完全在橋上的時間共40s, 求火車的速度和長度。
分析:解決這道問題,首先需要引導學生用部分代替整體,用火車上特別的一點(如車頭或車尾)來代替整列火車。
解:設火車的速度是xm/s,火車的長度為 ym。
根據題意得60x=1000+y40x+y=1000
列表格基本適用于任何題型。在應用表格分析問題時,只需要學生了解最基本的數量關系即可,如:路程=速度×時間;工作量=工效×時間;銷售額=單價×數量等等。現舉例如下:
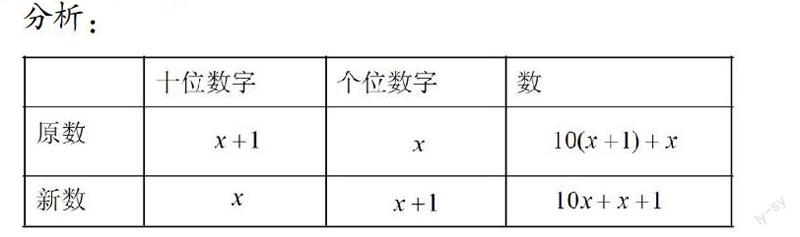
例2:已知一個兩位數,它的十位上的數字比個位上的數字大1,若顛倒個位數字與十位數字的位置,得到的新數比原數小9,求這個兩位數。
分析:
解:設這個兩位數的個位數字是x,則十位數字是x+1。
根據題意得[10(x+1)+x]-[10x+x+1]=9
方程應用題的教學是否應當遵循題型教學?這個問題沒有絕對的答案,老師的教學要因學生的整體水平靈活變化,只要適合學生的方法就是好方法!

