高速鐵路接觸線氣動參數仿真及風振響應研究

第一作者汪宏睿男，博士生，1990年生

通信作者劉志剛男，博士,教授，1975年生

高速鐵路接觸線氣動參數仿真及風振響應研究

汪宏睿，劉志剛，宋洋，姜靜

(西南交通大學電氣工程學院，成都610031)

摘要：為深入研究接觸網系統在風載荷作用下接觸線形成的風振響應，采用流體力學軟件Fluent模擬計算形狀不規則接觸線截面的氣動力參數，由其獲得接觸線與承力索的風載荷模型。在有限元軟件MSC-Marc中建立京津城際鐵路接觸網整體模型，并利用MSC-Marc用戶子程序功能實現接觸網中接觸線及承力索的風載荷動態輸入，求解得接觸線在不同風速、不同初始風攻角風載荷作用下產生的風振響應。結果表明，由于接觸線的氣動特性，任意風攻角風載荷作用下接觸線豎直方向振動位移均值為負值，會加劇弓網間相互作用；接觸線扭矩系數很小可忽略不計，接觸線發生馳振原因之一為升力系數隨攻角變化較大，在風攻角25°左右最可能發生馳振現象。

關鍵詞：風載荷；風振響應；氣動力參數；有限元；動態輸入；馳振

收稿日期：2013-11-08修改稿收到日期：2014-04-03

中圖分類號:LU225.7文獻標志碼：A

基金項目：國家自然科學

Aerodynamic parameters simulation and wind-induced vibration responses of contact wire of high-speed railway

WANGHong-rui,LIUZhi-gang,SONGYang,JIANGJing(School of Electrical Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Abstract:In order to study wind vibration responses of contact wire during a catenary system under wind load, the aerodynamic parameters of contact wires with irregular cross-section shapes were calculated using CFD software Fluent. The wind load models of contact wire and carrier cable were deduced based on the aerodynamic parameters. The finite element model of the catenary system was built by using MSC-MARC. Using the user subroutine of MSC-MARC, the dynamic input of the wind load on contact wire and carrier cable was realized. The wind vibration responses of contact wire under wind loads with different wind speeds and attack angles were simulated. The results showed that the mean vibration displacements of contact wire in vertical direction under wind load with any attack angle due to its aerodynamic characteristics are negative, they intensify the interaction between pantograph and contact wire; the torque coefficients of contact wire are small and can be ignored; the rapid change of lift coefficients of contact wire is one of the reasons to cause contact wire galloping; the galloping of contact wire is more possible to occur at the wind attack angle of 25°.

Key words:wind load; wind vibration response; aerodynamic parameters; FEM; dynamic input; galloping

由于高速鐵路接觸線截面形狀為帶溝槽的非標準圓形[1]，在風載荷作用下會造成接觸線偏移及振動，嚴重時會出現接觸網舞動甚至傾覆現象，易造成接觸線、吊弦、承力索損傷甚至斷線，縮短使用壽命，且影響機車受流，造成受電弓刮弓等事故。接觸線風偏值大小也是決定接觸網跨距長度設計值的重要指標。目前，國內外對高速鐵路接觸線在風載荷作用下產生振動的研究，尚未考慮接觸線特殊的截面形狀對氣動力參數影響[2-5]，而實際中接觸線在風作用下的受力與氣動參數直接相關，且模型往往只考慮接觸線的風載荷未考慮承力索的風載荷，因此研究計及接觸線氣動力參數及承力索風載荷接觸線風振具有重要意義。

對結構氣動力參數研究多采用風洞實測，但由于風洞實驗周期長、費用高、測量精度有限，且存在實驗模型與實際等效性難以確定的局限性[6]。因此，本文用計算流體力學(Computational Fluid Dynamics，CFD)軟件作為研究氣動特性的替代手段，模擬接觸線周圍流場并進行氣動力參數分析。先用CFD軟件Fluent模擬接觸線周圍定常空氣流場，計算不同迎風攻角下接觸線升力系數、阻力系數及扭轉力矩系數，分析不同風速下接觸線氣動參數變化規律，并與風洞實驗結果對比，驗證仿真的有效性；再據所得氣動力參數推導接觸線及承力索的風載荷模型，用MSC-Marc軟件建立接觸網整的有限元模型，利用Marc用戶子程序功能實現接觸網中接觸線及承力索風載荷的動態輸入；獲得接觸線在不同風速、初始風攻角風載荷作用下產生的風振響應特性。

1接觸線氣動力參數仿真計算

用Fluent對接觸線截面繞流進行模擬求得氣動力參數，需據接觸線截面實際形狀及尺寸繪制截面物理模型，再將截面周圍流場合理劃分網格，確定求解方法進行氣動力參數求解。

1.1模型建立

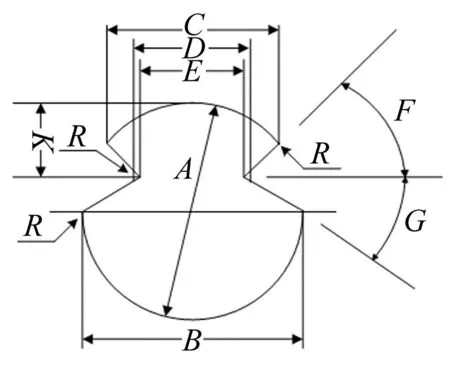
圖1　接觸線截面形狀 Fig.1 The cross-sectional shape of the contact line

高速鐵路常用的接觸線截面形狀見圖1，常用不同規格接觸線具體參數見表1。

由于接觸線合金類型識別溝槽對截面形狀影響較小且不具有統一形狀，忽略該溝槽對接觸線氣動力參數影響。四種規格接觸線直徑A或B的最大差值在4 mm以內，求解氣動力參數時因其截面形狀完全相同，尺寸對氣動力參數影響較小，因此選取典型的標稱截面積為120 mm2的接觸線建立物理模型。

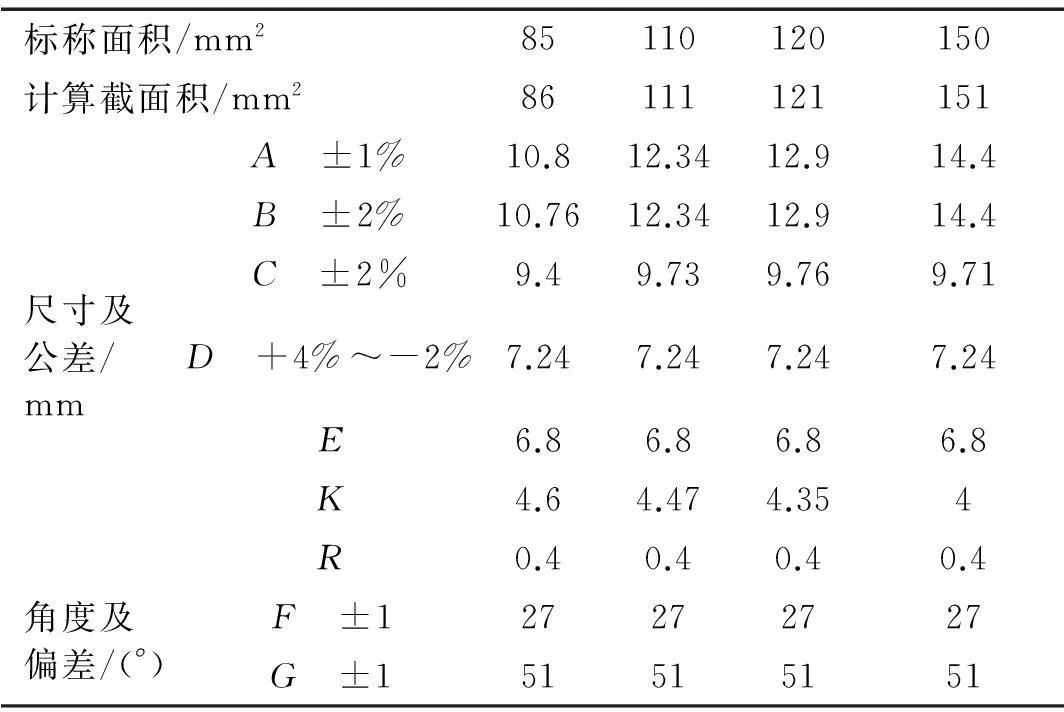
表1　接觸線截面規格參數

接觸線截面周圍計算域為流場，其網格劃分是求解氣動力參數關鍵。因此劃分時越近接觸線截面處網格應越密集，網格疏密需循序漸進，每層網格與相鄰內、外層網格面積比、長寬比不能過大。網格劃分有結構化與非結構化兩種，配合不同網格形狀與間距構成多種網格劃分形式。通過試驗多種網格劃分形式，考慮計算精度與效率，選擇圓形流場見圖2。網格為結構化網格，基本單元形狀為四邊形。圓形流場直徑4 m，流場平面總面積約12.57 m2，共劃分四邊形網格單元26 730個。流場的圓形外邊界定義為速度入口邊界(velocity-inlet)，用于具有一定速度的流體輸入；由于在流體作用下接觸線截面形狀不會發生改變，因此將截面邊界定義為固壁邊界(wall)。

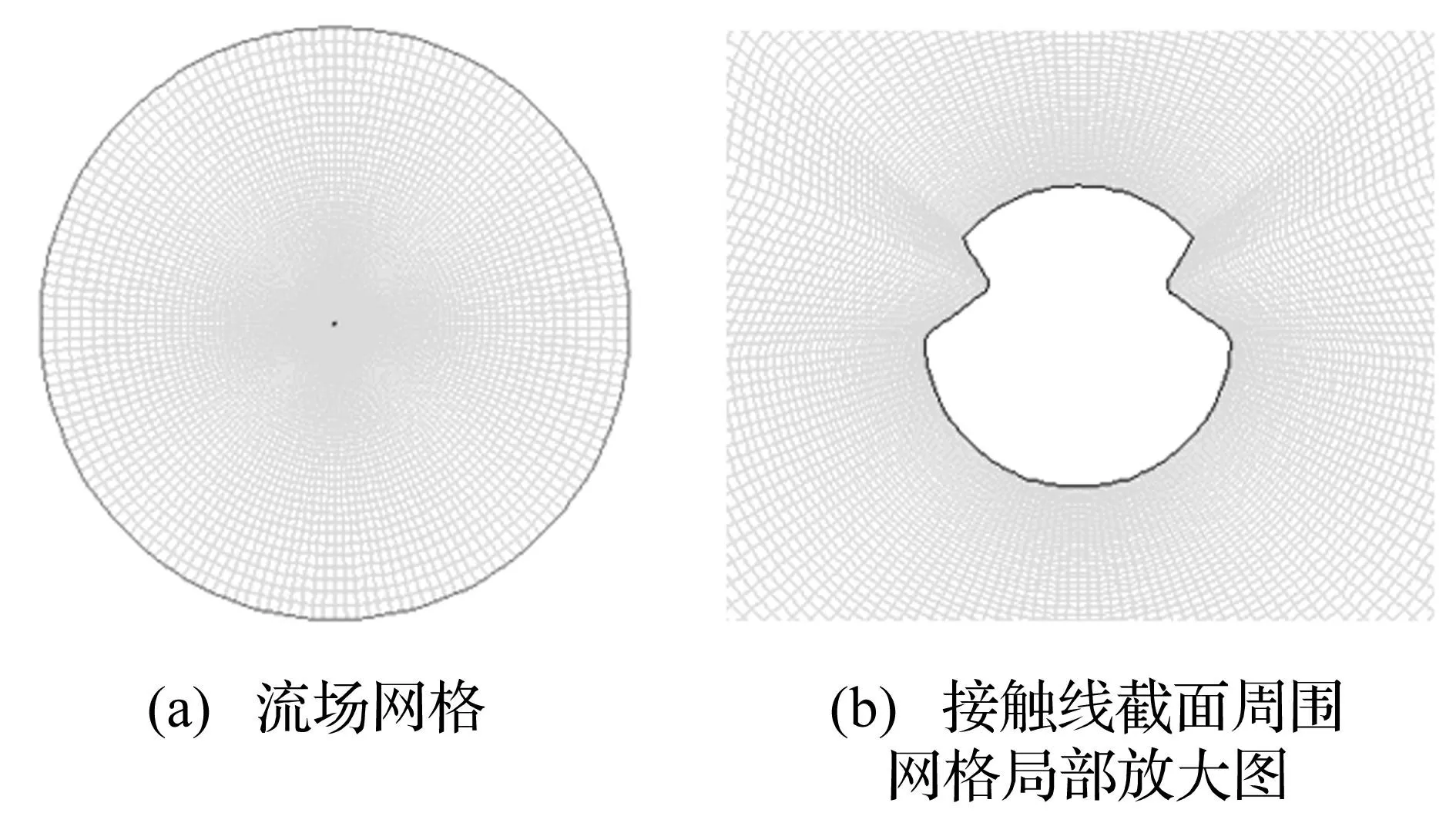
圖2　接觸線截面及流場網格 Fig.2 Cross-section of the contact line and its flow field grid

1.2仿真求解

流體因可壓縮性大小被分為可壓縮流體、不可壓縮流體兩類。可壓縮流體與速度密切相關，本文研究的接觸線周圍風速一般低于50 m/s，因而仿真時視風為不可壓縮流體，即流體外部壓強、溫度恒定使流體體積與密度恒定。

流體流動遵循動量守恒定理。不可壓縮流體在二維直角坐標系下動量守恒N-S方程[6]為

(1)

連續性方程為

(2)

式中：ρ為流體密度；μ為流體動力粘性系數；x，y為流體在直角坐標系下坐標；vx，vy為流體在流場中x，y方向速度；p，t分別為壓強、時間。

本文研究中流體的流動為端流流動，湍流模型選擇忽略分子粘性影響的完全湍流流動標準k-ε模型，該模型應用范圍廣且滿足本文精度要求。按模型設置Fluent求解器，對N-S方程及標準k-ε模型耦合求解，迭代直至殘差滿足收斂條件(殘差收斂值設為10-5)，得接觸線升力系數、阻力系數及力矩系數值。

1.3氣動力參數仿真結果及驗證

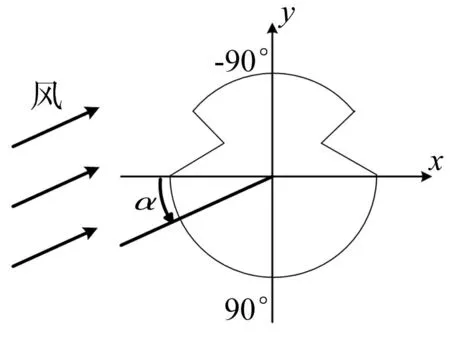
圖3　風攻角示意圖 Fig.3 Schematic diagram of wind attack angle

由于接觸線截面形狀左右對稱，故只需仿真風攻角-90°~90°時體軸的三分力系數，即得水平向阻力、豎直向升力和及扭轉力，經計算、轉換可得接觸線在任意風攻角下風軸的氣動力參數。本文選5 m/s，10 m/s，20 m/s及30 m/s四種風速，每種風速下風攻角由-90°~90°每隔5°進行一次仿真計算，風攻角α大小見圖3，即風向與x軸負半軸夾角，順時針方向為正。仿真結果表明，由于接觸線截面直徑較小，接觸線扭轉力矩系數數量級在10-3左右，與文獻[7]結論相同。因此在考慮風載荷對接觸線影響時可忽略其造成的扭轉力矩影響。仿真所得接觸線阻力、升力系數見圖4。由圖4看出，①接觸線截面不規則圓形造成氣動力參數不規則變化。接觸線阻力系數CD在風攻角由-60°增大到30°時出現類似波谷的變化，在-20°作用到夾持溝槽下表面時出現最小值，其它攻角下CD變化不大；接觸線升力系數CL隨風攻角變化出現兩個明顯波谷，第一個出現在-45°附近，此時風近似垂直作用在夾持溝槽下表面；第二個波谷出現在45°附近，其幅度變化明顯較第一個大，此時風近似垂直作用于夾持溝槽上表面；值得注意的是，接觸線升力系數在攻角0°~90°時均為負數(圖3中風向指向坐標軸第一區間)時，升力對接觸線作用實際上將其壓向坐標軸第四區間，即向右上方的風作用到接觸線上反而使其向右下方偏移。②風速對接觸線阻力系數CD及升力系數CL大小影響較大。在相同風攻角下，阻力系數CD及升力系數CL呈現隨風速增大而減小趨勢。

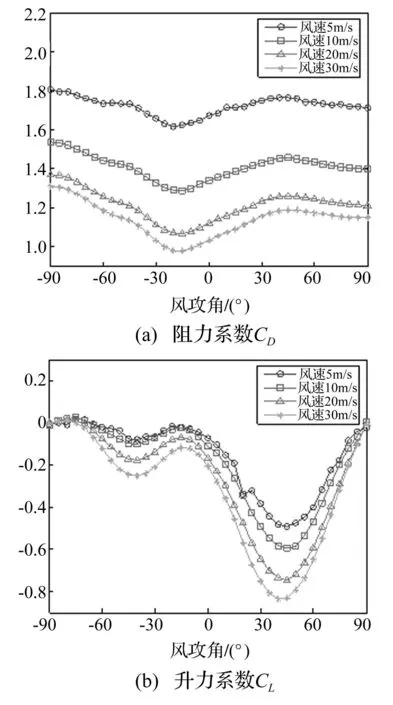
圖4　不同風速下接觸線氣動參數比較 Fig.4 Comparison of aerodynamic parameters of the contact lineunder different wind speeds

為驗證CFD仿真的有效性，在西南交通大學單回流串聯雙試驗段XNJD-1工業風洞內進行該型號接觸線截面實驗，見圖5。實驗按原接觸線5∶1的幾何比例制作模型，由于風洞實驗目的為驗證本文CFD仿真方法的有效性，因此只選取0°攻角下三個風速。實驗測得接觸線阻力系數見表2，與CFD仿真結果誤差在可接受范圍內，從而驗證本文方法的有效性。

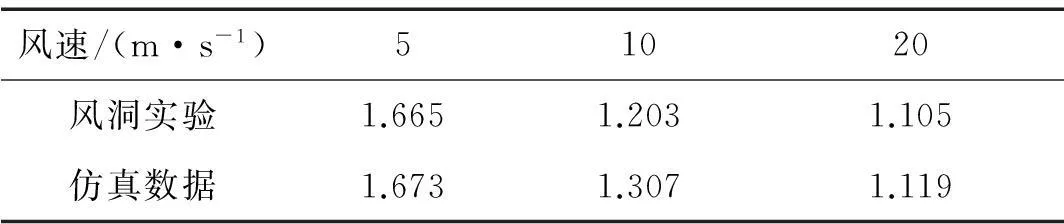
表2　風攻角0°時接觸線氣動力參數

圖5　風洞實驗現場圖 Fig.5 The experiment site of wind tunnel

為滿足數值計算要求，不同風速U下阻力系數CD及升力系數CL可擬合為風攻角α的三次多項式函數[8]。試驗后選α的5次多項式函數進行擬合以滿足精度要求,即

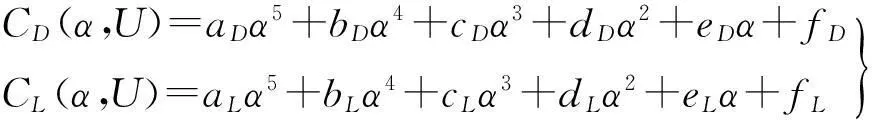
式中：aD，bD，cD，dD，eD，fD，aL，bL，cL，dL，eL，fL均為常系數。

2接觸線風振有限元模型

用有限元方法對接觸網受風振動響應進行仿真，模型由接觸網風載荷模型及接觸網有限元模型組成。

2.1接觸網風載荷

作用于建筑結構的風載荷由平均風與脈動風兩部分產生，分別為靜態力與動態力[9]。對柔性結構接觸網而言，風載荷作用直接導致接觸網的振動及形變，進而導致有效風攻角改變，使平均風及脈動風對接觸網均產生動態力作用，致接觸線產生復雜的振動現象。接觸網空間隨機風場的模擬方法文獻[3]已詳述，用Davenport風譜、空間互譜密度函數及諧波疊加法模擬接觸網中多個特征點的風速時程。據各特征點風速時程，在有限元模型中模擬不同平均風速及初始風攻角下接觸網風載荷，獲得接觸線振動情況。

自然風載荷對接觸線或承力索的作用為定常空氣力[10]，據流體誘發振動理論，長L的接觸線在速度U的風作用下，所受氣動力載荷包括順風向阻力FD、垂直順風向升力FL及扭轉力矩FM。由于接觸線扭轉力矩系數CM非常小可忽略不計，故接觸線所受阻力、升力[11]可分別表示為

(4)

(5)

式中：ρ為空氣密度；U為平均風速；D為接觸線直徑；L為接觸線長度；CD(α,U)，CL(α,U)為在風速U下有效風攻角為α時接觸線阻力系數與升力系數的函數(見式(3));振動時接觸線的有效風攻角α為

α=α0+β-Δα

(6)

式中：α0為初始風攻角；Δα為接觸線自身扭轉角；β為接觸線動態迎風角。

由于β的存在，當來流風速為U時，接觸線實際受力見圖6。圖中Fx軸與Fy軸圍成的坐標系稱絕對風軸坐標系，由初始風攻角α0決定。FD軸與FL軸圍成的坐標系稱相對風軸坐標系，由動態迎風角β決定。ux，uy分別為接觸線特征點處水平、豎直方向速度。在相對風軸坐標系中，FD與FL由式(4)、(5)決定，將其轉化到絕對風軸坐標系得

Fx=FDcosβ-FLsinβ

(7)

Fy=FDsinβ+FLcosβ

(8)

式中：動態迎風角β由導線豎直方向振動引起，表達為

(9)

由于接觸線振動時U?uy，故上式可簡化為

(10)

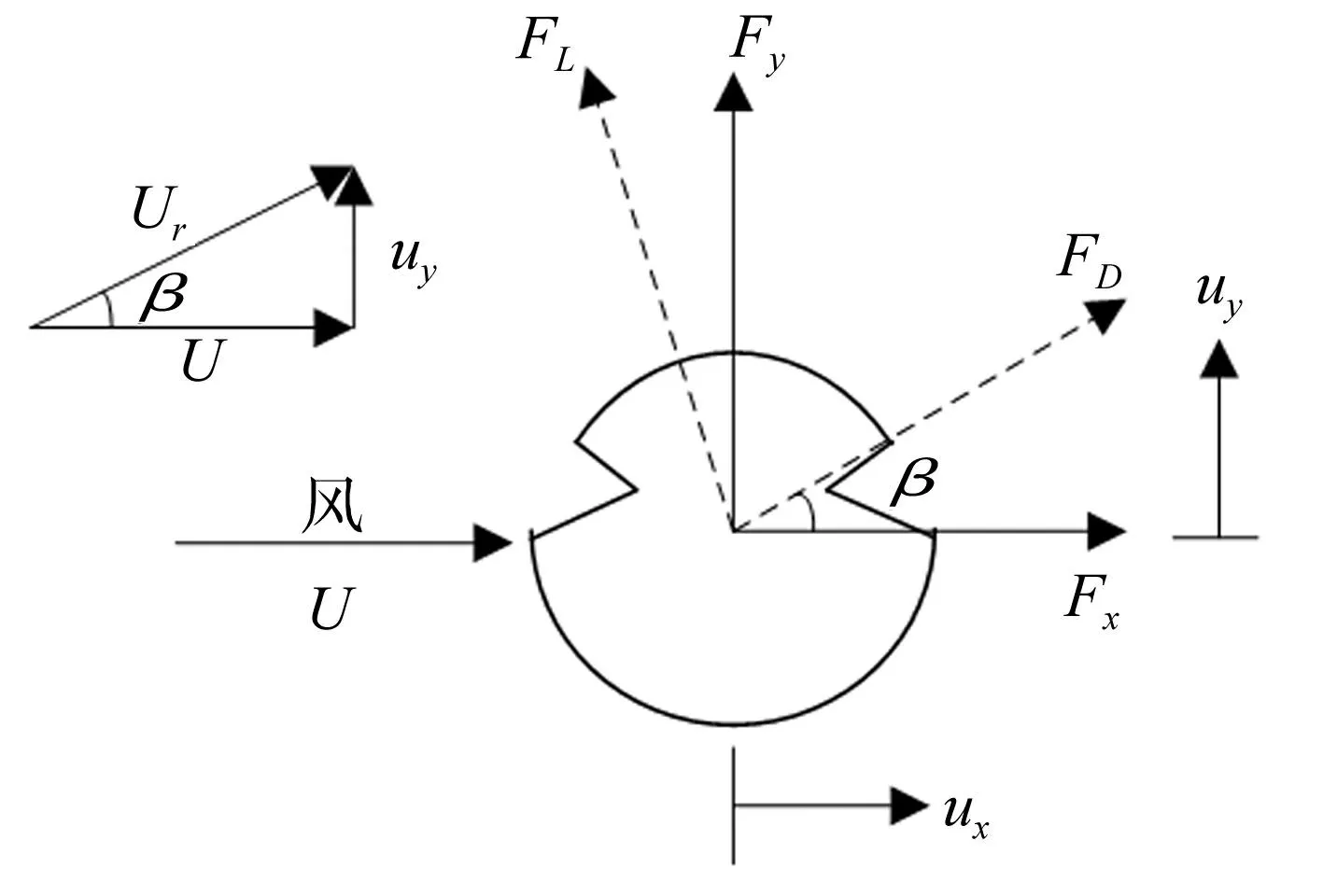
圖6　接觸線截面迎風示意圖 Fig.6 Schematic diagram of the contact line section windward

由于承力索截面為標準圓形，取阻力、升力系數分別為1與0，按同樣推導過程，作用在承力索的風載荷可表示為

(11)

式中：FAD，FAL為承力索所受阻力、升力；FAx，FAy為承力索在絕對風軸坐標系中所受水平、豎直方向力；βA為承力索動態迎風角，由承力索節點處豎直方向運動速度uAy及風速U決定。

2.2風載荷動態輸入

由于式(7)、(8)、(11)的接觸線、承力索所受風載荷均隨接觸線或承力索自身扭轉角度Δα及動態迎風角β變化而變化，故進行有限元分析時需實現動態變化的風載荷實時更新、輸入。用Marc用戶子程序功能提取Marc中每一增量步的計算結果，按式(4)~式(11)更新作用在接觸線的風載荷大小。具體流程見圖7。

圖7　風載荷施加流程圖 Fig.7 The flow chart of the apply of wind load

2.3接觸網有限元模型

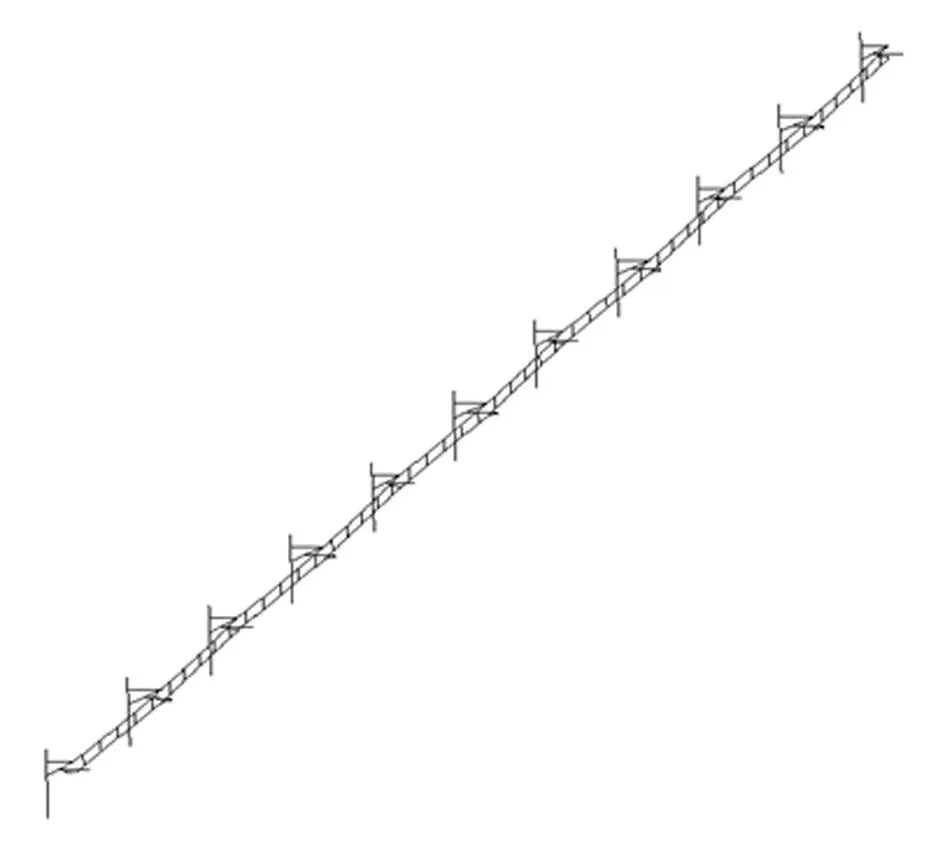
圖8　接觸網有限元模型 Fig.8 The FEM of catenary system

采用有限元分析軟件MSC-Marc建立接觸網的有限元模型，以京津城際鐵路實際參數為例建立一個錨段的接觸網模型，具體參數見表3。京津線所用接觸線型號為CTMH120，與氣動力參數仿真模型所用接觸線參數一致。接觸線、承力索采用歐拉—伯努力梁單元，正反定位器及支撐桿簡化為梁單元，通過鉸鏈與碗臂連接。考慮重力對接觸網影響，接觸線、承力索及吊弦等考慮為分布質量，錨段兩端固定約束，接觸網整體有限元模型見圖8。用本文建模方法建立EN50318標準參數模型。該模型仿真結果符合EN50318要求，由此表明本文接觸網模型可信度較高。

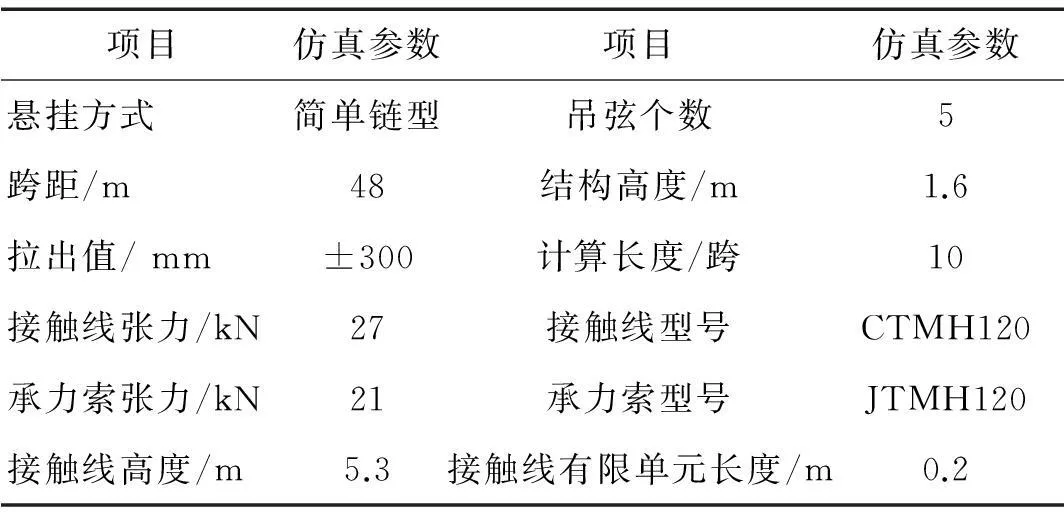
表3　接觸網有限元模型參數

3接觸線風振響應計算結果分析

在接觸網有限元模型中施加風載荷需在接觸線及承力索上選取合適特征點。選每個定位點及跨中點對應的接觸線及承力索節點作為施加風載荷特征點，即接觸線及承力索相鄰特征點間距為24 m，對應模擬平均風速為5 m/s，10 m/s，20 m/s，30 m/s計42個特征點風速時程，用諧波疊加法進行風場模擬，具體參數見表4。圖9為由上至下平均風速為10 m/s時特征點1、20、40的風速時程。

據所得風速時程及接觸線阻力、升力系數用有限元模型仿真初始風攻角分別為-70°，-40°，-10°，0°，10°，40°，70°時接觸網在風載荷作用下的接觸線振動。采樣間隔0.1 s，仿真增量步總數1 000與風場模擬數據對應。

表4　風場模擬參數

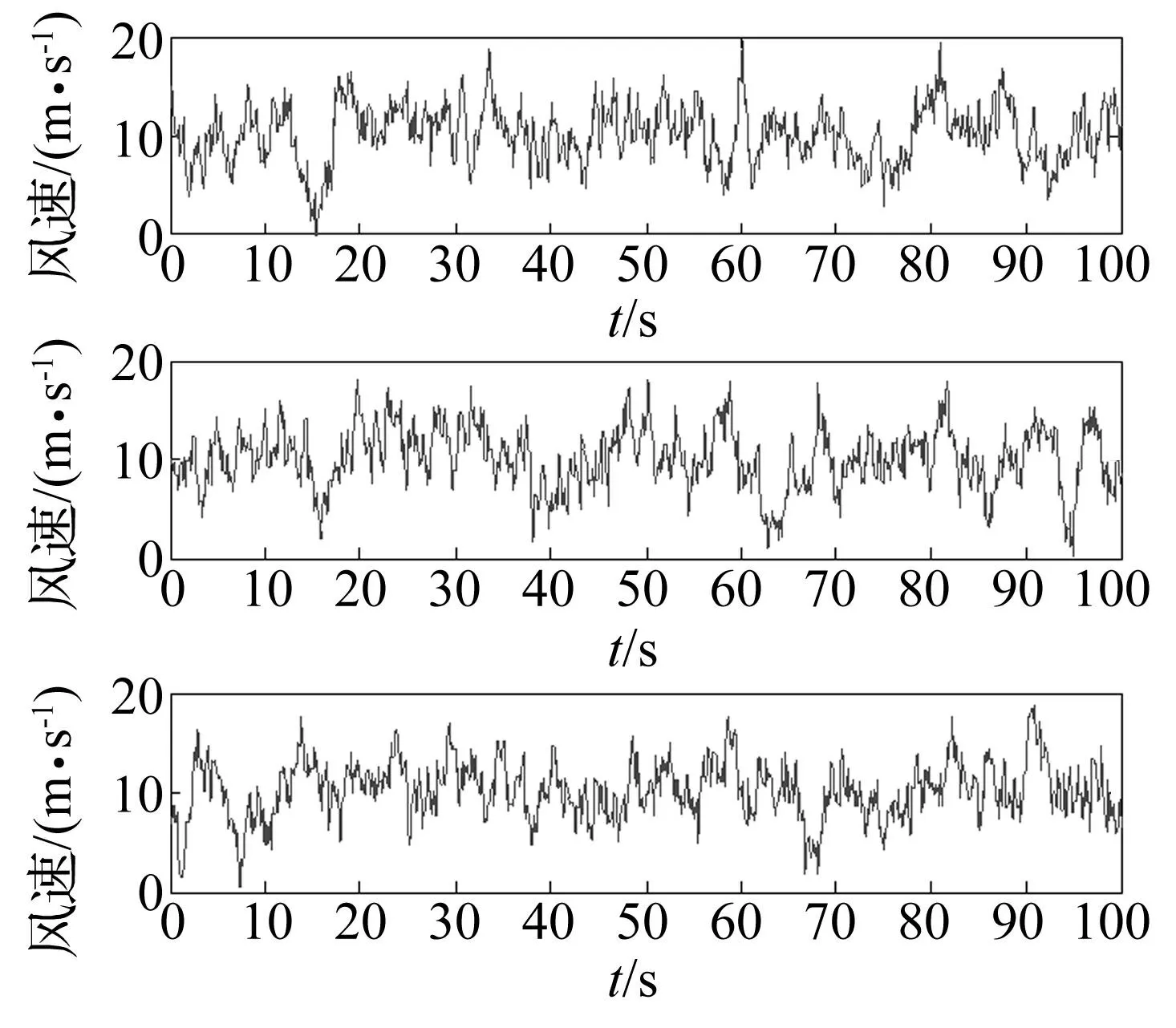
圖9　平均風速10 m/s時特征點1、20、40風速時程 Fig.9 The time series of wind velocity of feature points 1,20 and 40

3.1接觸線風振響應

接觸線振動幅度必隨風速增大而增大，一般在每跨中點振幅最大。圖10為部分風速、攻角下接觸線特征點相對無風時初始位置位移時程，特征點為錨段內第五跨接觸線中點。由圖10(a)、(b)看出，風攻角變化明顯影響接觸線豎向位移大小，但對水平向位移影響較小。10 m/s風速、攻角10°及40°的水平位移均值只相差約0.4 mm，此處若不考慮接觸線氣動參數影響，在相同平均風速下水平位移均值之比應近似于cos10°/cos40°，但事實上(圖4(b))攻角40°時，接觸線升力系數近似達負方向最大值，即該氣動參數值使40°攻角下接觸線水平向風載荷變大，因此本文計算結果更準確。由圖10(b)、(c)看出，平均風速大小決定接觸線水平與豎直方向整體偏移幅度及振幅，接觸線振動主要由脈動風引起。攻角40°時由于升力系數為負，接觸線豎向位移均值為負，由此驗證本文分析的正確性。

風攻角為40°時不同風速下特征點位移時程統計量見表5，表中x，y分別表示水平、豎直方向位移。由表5看出，對大張力小跨距的接觸網系統而言，接觸線的平均位移及振幅隨風速增大而增大，出現刮弓概率隨之增大。平均風速為20 m/s時，不同風攻角下特征點平均位移見圖11。由圖11看出，考慮氣動特性時接觸線平均位移隨攻角呈規律變化，在攻角40°處水平、豎直位移均較大，因而對接觸線影響較大。綜合表5、圖11及圖4(b)的升力系數曲線知，接觸線升力系數在攻角0°~90°時均為負數，而攻角-90°~0°時使接觸線豎向位移均值為負，因此在任意風攻角風載荷作用下，接觸線的豎向偏移均值為負值，吊弦、承力索及定位器的作用會減弱該偏移量，但仍會加劇受電弓與接觸線間相互作用，影響受流質量。

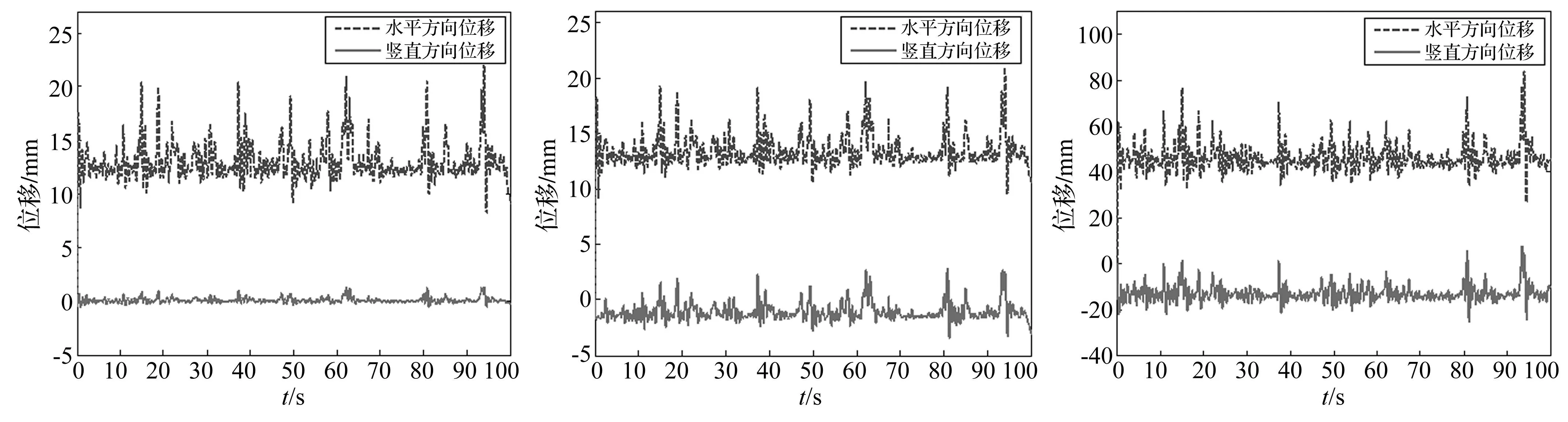
(a) 風速10m/s攻角10°時特征點位移時程(b) 風速10m/s攻角40°時特征點位移時程(c) 風速20m/s攻角40°時特征點位移時程圖10 不同風速、攻角下特征點位移時程Fig.10Thetimeseriesofdisplacementoffeaturepointunderdifferentwindspeedandattackangle

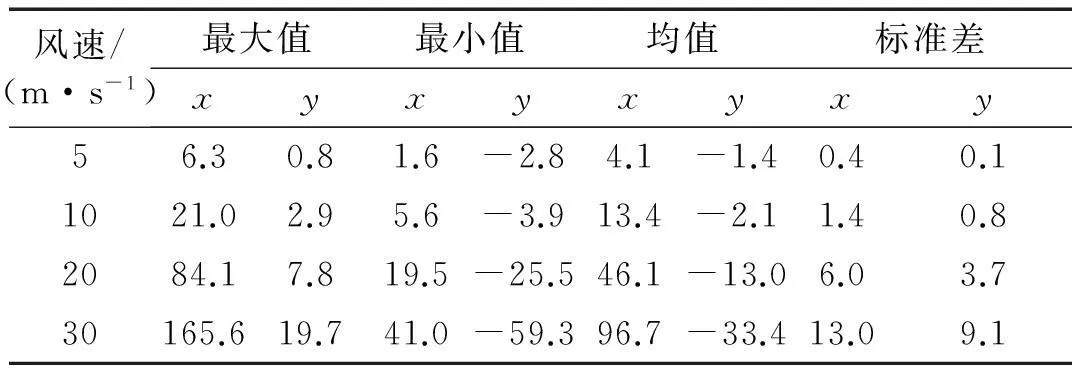
表5　不同風速下接觸線振動響應位移統計量(單位：mm)

對一個錨段內10跨接觸網結構，接觸線的平均偏移量與距錨段兩端距離及正反定位相關。圖12為風攻角0°時不同風速下接觸線各跨中點歸一化平均水平位移。由圖12看出，位于錨段兩端的第一跨、第十跨接觸線振幅最小，且由外向內變大的同時又因正反定位器交替出現振蕩現象,振幅在位于錨段中間第五、第六處達到平衡值。風速越大該變化趨勢越不明顯。

3.2接觸線馳振初探

氣動力參數仿真結果表明，接觸線在不同風速下的扭轉力矩系數均較小，風對接觸線的扭轉作用可忽略不計；而接觸線升力系數變化較大，可用鄧哈托垂直振動理論判別其馳振穩定性。據該理論，結構發生馳振的必要條件為橫風向鄧哈托系數小于0，即

(12)

式中：δD為橫風向鄧哈托系數。

實際的接觸線發生馳振風速約8~15 m/s。據仿真所得氣動力參數，計算10 m/s風速下接觸線橫風向鄧哈托系數，見圖13。由圖13看出，接觸線在風攻角15°~30°間橫風向鄧哈托系數為負，可能發生馳振，其中在風攻角25°處最易發生馳振。

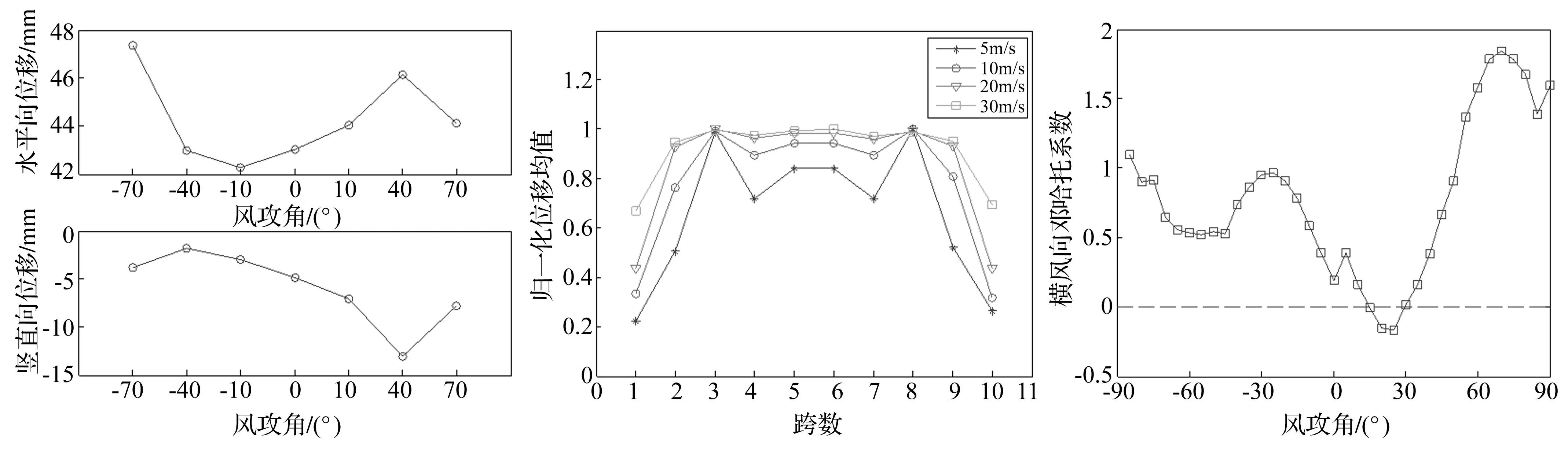
圖11 不同風攻角下接觸線振動響應位移均值Fig.11Themeandisplacementofcontactwirevibrationresponseunderdifferentwindattackangles圖12 錨段內各跨接觸線中點水平位移均值Fig.12Themeanhorizontaldisplacementofeveryspanmidpointinananchorsection圖13 10m/s風速下接觸線橫風向鄧哈托系數Fig.13TheDenHartogcoefficientsofcontactwireunderwindspeedof10m/s

以風速10 m/s、風攻角25°為條件按本文方法進行有限元仿真，所得特征點處水平、豎直方向位移見圖14。由圖14看出，接觸線未發生馳振現象，原因為接觸線并非獨立結構，在考慮馳振時不可忽視承力索、吊弦、定位器等裝置對其約束作用以及覆冰、空氣濕度等環境因素，因此接觸線馳振形成原因復雜，有待進一步研究。

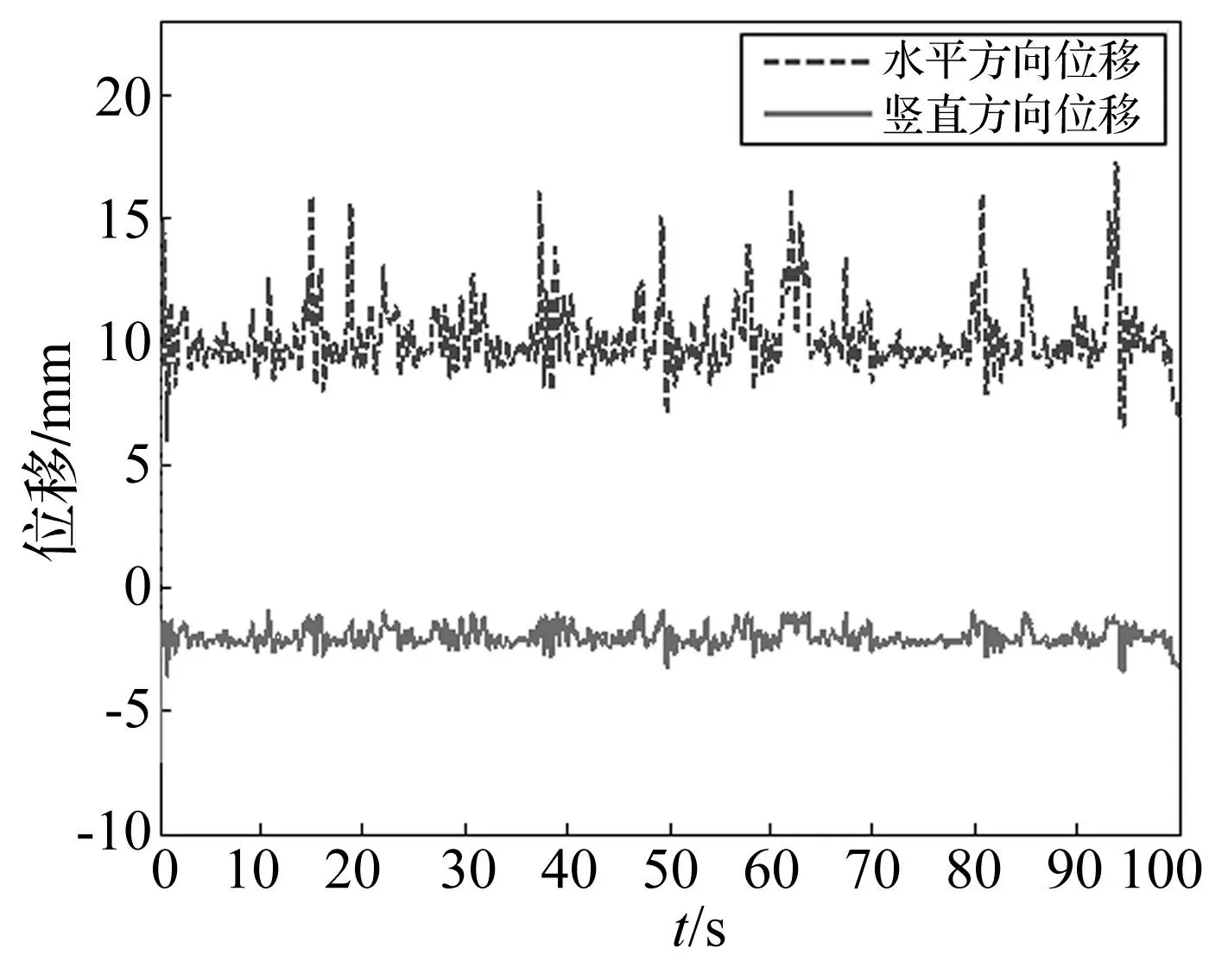
圖14　風速10 m/s、風攻角25°下接觸線位移時程 Fig.14 The time series of displacement of contact wire under wind speed of 10m/s and attack angle of 25°

4結論

(1)由于接觸線截面存在夾持溝槽，其阻力系數、升力系數隨風攻角及風速變化呈不同大小，而扭轉力矩系數可忽略。

(2)考慮氣動力參數時接觸線所受風載荷隨有效風攻角變化。在任意風攻角風載荷作用下，接觸線豎直方向位移均值為負值，會加劇弓網的相互作用。其中風攻角為40°時接觸線水平、豎直方向位移均較大。

(3)接觸線發生馳振原因之一為升力系數隨攻角變化。25°風攻角時最可能發生馳振現象，但只考慮升力系數變化單一因素時接觸線不易發生馳振現象。

參考文獻

[1]吳積欽. 受電弓與接觸網系統[M]. 成都：西南交通大學出版社，2010.

[2]曹樹森，柯堅，鄧斌，等．強風地區接觸網動力穩定性分析[J]．中國鐵道科學，2010, 31(4): 79-84.

CAO Shu-sen, KE Jian, DENG Bin,et al. The dynamic stability analysis of the catenary systems in strong wind area[J].China Railway Science, 2010,31(4): 79-84.

[3]趙飛，劉志剛，韓志偉．隨機風場對弓網系統動態性能影響研究[J]．鐵道學報，2012, 34(10): 36-42.

ZHAO Fei，LIU Zhi-gang，HAN Zhi-wei．Simulation study on influence of stochastic wind field to dynamic behavior of pantograph-catenary system[J]．Journal of the China Railway Society, 2012, 34(10): 36-42.

[4]潘洪海. 基于ANSYS的接觸線風偏計算[J]. 電氣化鐵道，2009, 5: 33-39.

PAN Hong-hai. Calculation of wind deviation of contact wire based on ANSYS[J]. Electric Railway, 2009,5: 33-39.

[5]韓佳棟,曹樹森,劉曉紅,等. 強風地區接觸網風振響應分析[J]. 鐵道建筑技術，2010(S): 207-210.

HAN Jia-dong, CAO Shu-sen,LIU Xiao-hong,et al. Wind vibration response analysis of contact wire in the strong wind area[J]. Railway construction technology, 2010 (S): 207-210.

[6]王少華. 基于Fluent的覆冰導線氣動特性分析[J]. 高壓電器,2012,48(1): 36-42.

WANG Shao-hua. Analysis of aerodynamic characteristics of iced conductor based on fluent[J]. High Voltage Apparatus, 2012,48(1): 36-42.

[7]謝強,王巍,李海若. 高速鐵路接觸線氣動力特性的風洞試驗研究[J]. 中國鐵道科學,2012,33(6): 75-82.

XIE Qiang, WANG Wei, LI Hai-ruo. Wind tunnel test on the aerodynamic characteristics of contact wire for high-speed railway[J]. China Railway Science, 2012, 33(6): 75-82.

[8]曹化錦,李黎,姜維,等. 輸電塔-線體系舞動仿真及控制研究[J]. 振動與沖擊,2011,30(12): 245-249.

CAO Hua-jin, LI Lin, JIANG Wei, et al. Simulation and control for galloping of a transmission tower-line system[J]. Journal of Vibration and Shock, 2011,30(12): 245-249.

[9]孫振. 建筑結構風載荷的計算機模擬與分析[D]. 南京：南京航空航天大學, 2007.

[10]周坤濤,郝淑英,劉君,等. 覆冰輸電線結構及載荷對舞動的影響[J]. 振動與沖擊,2012,31(1): 116-120.

ZHOU Kun-tao, HAO Shu-ying, LIU Jun, et al. Influence of conductor structure and loads on galloping of a transmission line[J]. Journal of Vibration and Shock, 2012, 31(1): 116-120.

[11]趙莉,嚴波,蔡萌琦,等. 輸電塔線體系中覆冰導線舞動數值模擬研究[J]. 振動與沖擊,2013, 32(18): 113-120.

ZHAO Li, YAN Bo, CAI Meng-qi, et al. Numerical simulation for galloping of iced conductors in a transmission tower-line system[J]. Journal of Vibration and Shock, 2013, 32(18): 113-120.

[12]孫珍茂，樓文娟. 覆冰輸電導線舞動及防舞效果分析[J]. 振動與沖擊,2010,29(5): 141-146.

SUN Zhen-mao, LOU Wen-juan. Analysis of iced transmission line galloping and effect of anti-galloping[J]. Journal of Vibration and Shock, 2010,29(5): 141-146.

[13]Desai Y M, Shan A H, Popplewell N. Perturbation based finite element analyses of transmission line galloping[J]. Journal of Sound and Vibration, 1996, 191(4): 469-489.

[14]吳燕,吳俊勇,鄭積浩．高速受電弓-接觸網系統動態受流性能的仿真分析[J].北京交通大學學報,2009,33(5):60- 63.

WU Yan, WU Jun-yong, ZHENG Ji-hao. A simulation study on current collection of high-speed pantograph-catenary[J].Journal of Beijing Jiaotong University, 2009, 33(5): 60-63.

[15]孫珍茂,樓文娟．覆冰輸電導線舞動非線性有限元分析[J]. 電網技術,2010, 34(12): 214-218.

SUN Zhen-mao, LOU Wen-juan. Nonlinear finite element analysis on galloping of ice-coated transmission line[J]. Power System Technology, 2010, 34(12): 214-218.