鋼筋混凝土梁動態試驗與數值模擬

第一作者李敏女，博士，講師，1981年生

郵箱:cnlm225@126.com

鋼筋混凝土梁動態試驗與數值模擬

李敏1，李宏男2

(1.大連海洋大學海洋與土木工程學院，遼寧大連116023； 2.大連理工大學 建設工程學部，遼寧大連116024)

摘要：試驗研究、數值模擬地震作用范圍內加載速率對鋼筋混凝土梁影響。試驗研究混凝土強度、鋼筋強度、剪跨比、加載速率及加載模式等對鋼筋混凝土梁力學及變形性能影響；基于ABAQUS有限元軟件建立鋼筋混凝土梁計算模型，考慮鋼筋、混凝土的率敏感性，對梁試件在不同工況下動態性能進行數值模擬；模擬結果與試驗結果吻合較好。

關鍵詞：加載速率；鋼筋混凝土梁；地震作用；試驗研究；數值模擬

收稿日期：2014-01-08修改稿收到日期：2014-03-12

中圖分類號:TU375文獻標志碼：A

Dynamic tests and numerical simulation of reinforced concrete beams

LIMin1,LIHong-nan2(1. School of Marine and Civil Engineering, Dalian Ocean University, Dalian 116023, China； 2. Faculty of infrastructure Engineering, Dalian University of Technology, Dalian 116024, China)

Abstract:The effects of loading rate that might be experienced during earthquakes on reinforced concrete beams were experimentally and numerically studied here. Firstly, the effects of loading rate on mechanical properties and deformation of reinforced concrete beams were experimentally studied with the variation of several parameters including concrete strength, steel strength, shear span ratio, loading rate and loading mode. Then, based on the finite element software ABAQUS, considering the strain rate sensitivity of concrete and steel, the dynamic performances of reinforced concrete beams under different loading conditions were simulated, and the simulation results agreed well with the test ones.

Key words:loading rate; reinforced concrete beam; seismic loading; experimental study; numerical simulation

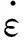
本文試驗研究、數值模擬加載速率對鋼筋混凝土梁的影響。考慮混凝土強度、鋼筋強度、剪跨比及加載模式等參數，試驗研究加載速率對鋼筋混凝土梁力學及變形性能影響；并基于ABAQUS有限元軟件建立鋼筋混凝土梁計算模型，考慮鋼筋、混凝土的率敏感性對梁試件在不同工況下的動態性能進行有限元數值模擬。

1試驗內容

1.1試驗概況

本試驗所用鋼筋混凝土梁共16根，長度均2 500 mm, 截面為矩形150 mm×250 mm，保護層厚30 mm。縱筋直徑18 mm，配筋率1.6%；箍筋直徑6.5 mm, 間距200 mm，配筋率0.22%。試件設計考慮混凝土強度等級(C30，C50)、縱筋強度等級(HRB335，HRB400)、剪跨比(λ=5.5，λ=3.0)、加載方式(單調及循環加載)、加載速率(0.05 mm/s，30 mm/s)。試驗梁尺寸及配筋見圖1。試件參數及不同工況下模擬與試驗結果承載力見表1，其中試件編號含義為：B代表梁試件，30代表C30混凝土，50代表C50混凝土，S代表準靜態加載，D代表快速加載，M代表單調加載，C代表循環加載，1代表剪跨比5.5，2代表剪跨比3。C30及C50混凝土試件(邊長100 mm)立方體抗壓強度實測值分別為36.94 MPa及49.22 MPa，HRB335及HRB400鋼筋屈服強度實測值分別為381.62 MPa及428.25 MPa，箍筋屈服強度實測值為388.9 MPa。

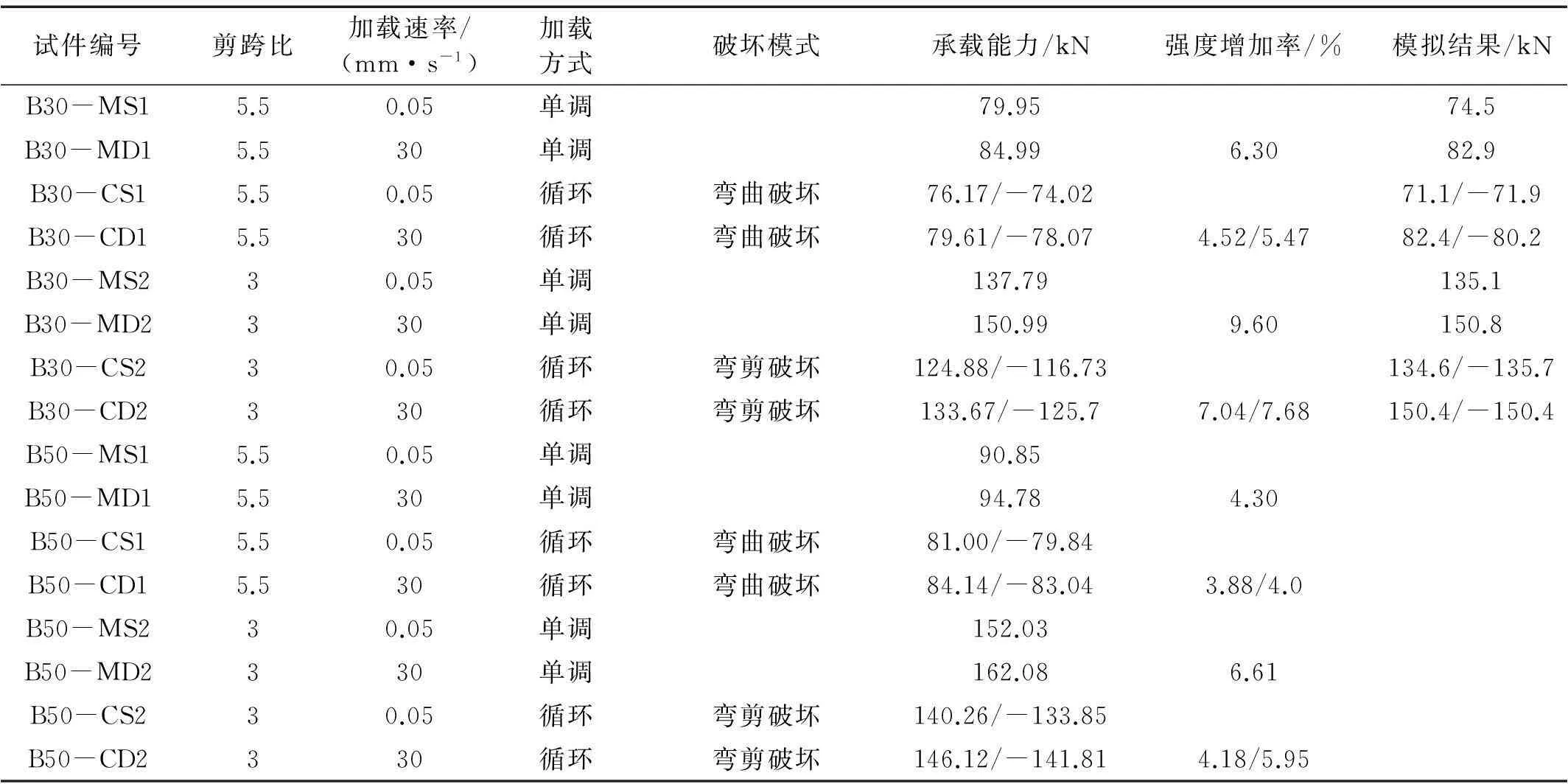
表1　試件參數及試驗、模擬結果

注：表中承載能力為屈服段(上升段)最大承載力。

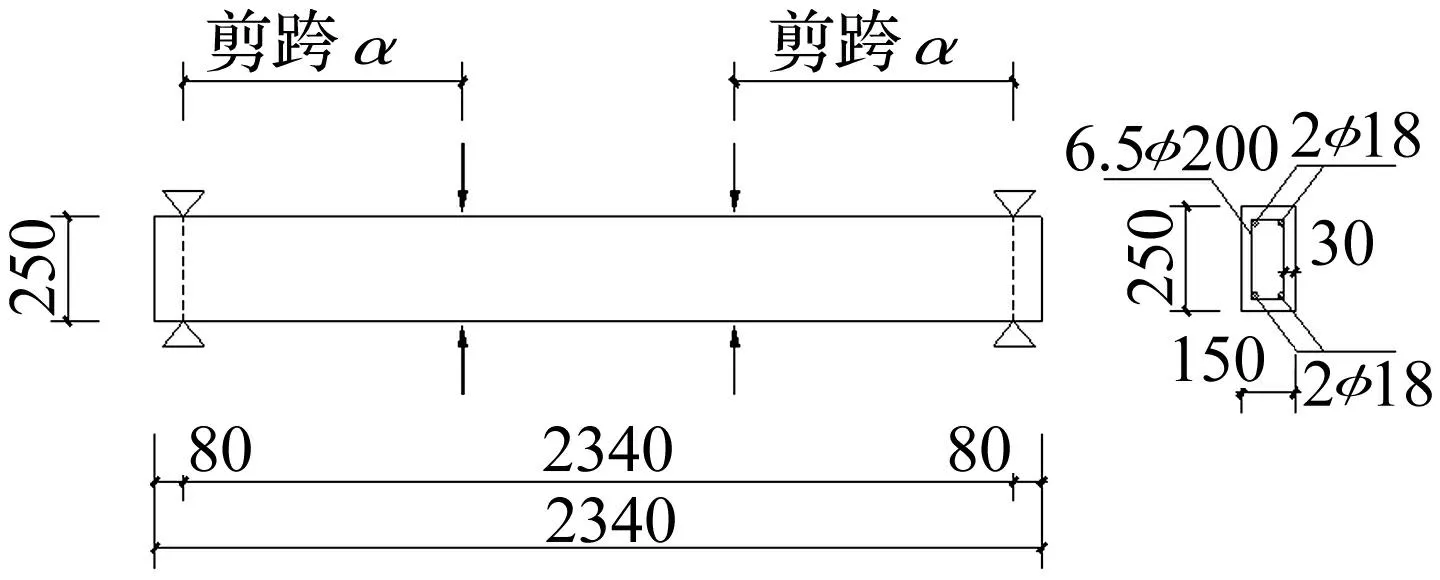
圖1　試驗梁尺寸、配筋示意圖(單位：mm) Fig.1 Dimension and reinforcement of the beam

試驗在大型靜動三軸電液伺服試驗機上進行，采用單調加載及三角波循環加載，見圖2。循環加載幅值取屈服位移的整數倍(屈服位移定義為縱筋首次屈服時梁跨中位移)，每個幅值循環一次，采用位移控制模式加載，速率保持不變，慢速加載速率為0.05 mm/s,并與準靜態加載對應；快速加載速率為30 mm/s，與地震作用時快速加載對應。

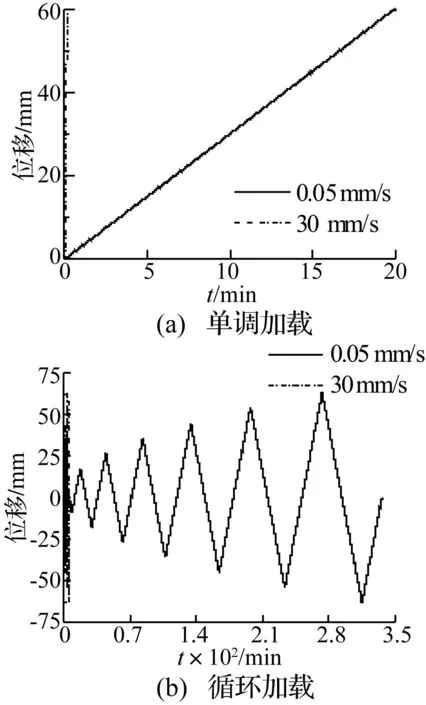
圖2　兩種加載方式 Fig.2 Two kinds of loading modes

1.2試驗結果

據采集的數據，慢速加載時梁跨中受拉鋼筋最大應變率量級為10-5/s, 快速加載時梁跨中受拉鋼筋最大應變率量級為10-3/s, 剪跨段箍筋最大應變率量級為10-3/s。本文加載應變率量級在地震應變率范圍(10-5/ s～10-1/s)，因此試驗結果對研究地震作用下鋼筋混凝土結構、構件響應有一定意義。

由試驗所得各工況下鋼筋混凝土梁跨中荷載-撓度曲線見圖3。每種工況下梁的極限承載力見表1。由試驗結果知：隨加載速率提高各工況下梁的承載力均得到提高,組成梁的材料強度越高承載力提高越少。原因為混凝土、鋼筋均為率敏感性材料，且應變率敏感性大小與強度成反比。對具有相同材料強度的梁，剪跨比越大，承載力提高越小。此因加載速率相對于加載點，剪跨比為5.5時加載點在跨中，而剪跨比為3時加載點與跨中距離為537 mm。因此對整根梁而言，剪跨比為3的梁實際加載速率較剪跨比為5.5的梁快，承載力提高的也多。

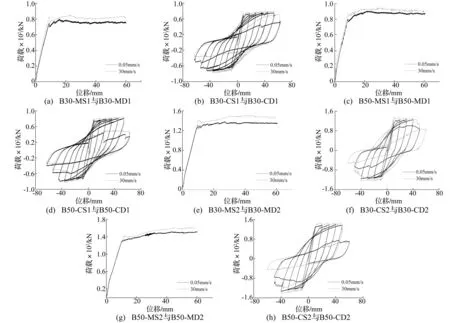
圖3　不同加載速率下鋼筋混凝土梁跨中荷載-撓度曲線 Fig.3 Load-displacement curves in the midspan of beams at different loading rates

對具有相同材料強度及剪跨比的梁，隨加載速率提高循環加載較單調加載時強度增加少。此現象可能因在動態循環轉折點位置鋼筋、混凝土應變率幾乎為零，而單調加載時鋼筋、混凝土應變率大于零，因此循環加載對加載速率的敏感性較單調加載時小。

2數值模擬

2.1計算模型

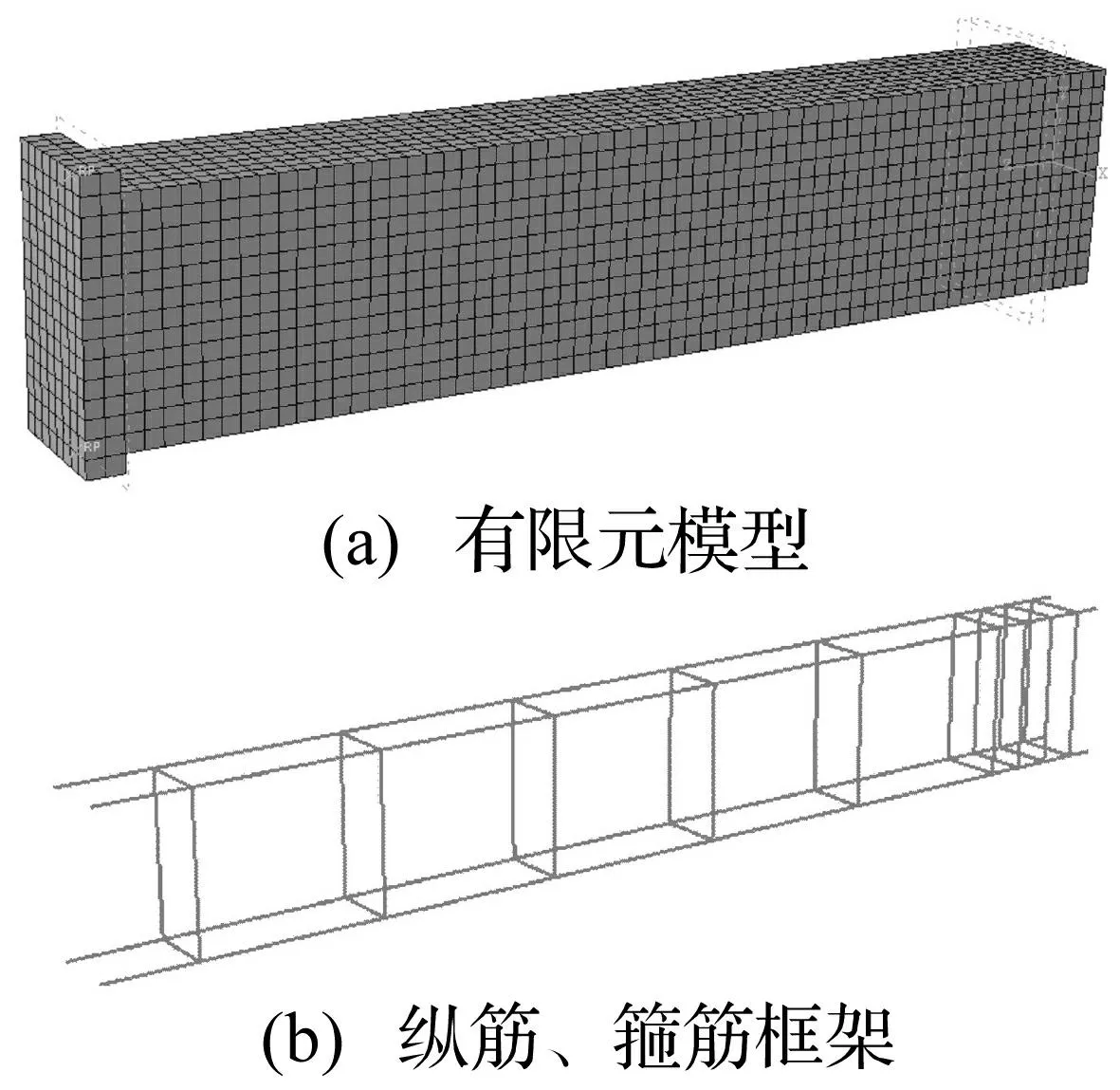
圖4　鋼筋混凝土梁有限元模型 Fig.4 Finite element model of reinforced concrete beam

用ABAQUS有限元軟件對試驗鋼筋混凝土梁建模，由于梁試件具有對稱性，為提高計算效率，取一半梁建模。混凝土采用8節點六面體減縮積分單元C3D8R，縱筋、箍筋采用2節點空間桁架單元T3D2，通過Embeded方式嵌入混凝土中，鋼筋、混凝土間粘結滑移及裂縫間應力傳遞通過*tension stiffening命令近似模擬。混凝土單元尺寸20 mm×20 mm×20 mm,鋼筋單元尺寸20 mm。用位移控制模式加載，為避免應力集中,在加載點放置剛性塊，通過控制剛性塊位移間接對梁試件加載。該梁有限元模型及縱筋、箍筋框架見圖4。由于模擬主要關心加載速率對鋼筋混凝土梁性能影響，故采用Dynamic,Explicit求解器顯式求解。

2.2材料模型

2.2.1鋼筋模型

鋼筋模型應能模擬屈服面形狀大小變化及Baushinger效應，且可考慮快速加載時鋼筋的應變率效應；但由于試驗所得最大鋼筋應變基本處于屈服階段或剛進入強化階段，因此本文不考慮鋼筋的強化，采用Mises模型模擬鋼筋的本構關系，即用公式[11]模擬鋼筋屈服強度的應變率效應。鋼筋的動態與準靜態屈服強度關系為

(1)

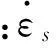
2.2.2混凝土模型

采用ABAQUS中混凝土損傷塑性模型模擬混凝土[12]。定義混凝土損傷塑性模型，需提供混凝土單軸拉、壓率相關本構方程。

(1)混凝土單軸受壓率相關本構方程

據已有研究成果，混凝土單軸名義受壓應力-應變曲線形狀與應變率無關。本文對不同應變率下混凝土單軸名義受壓應力-應變曲線取相同表達形式。采用混凝土單軸受壓本構關系[13]，其單軸受壓率相關本構方程為

y=aax+(3-2aa)x2+(aa-2)x3， (x≤1 )

(2)

(3)

(4)

(5)

式中：aa、ad分別為上升、下降段參數；fcu為混凝土準靜態立方體抗壓強度(MPa)；DIF為混凝土單軸動態立方體與準靜態立方體抗壓強度比值，表達式[14]為

C30混凝土：

(6)

C50混凝土：

(7)

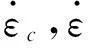
(2)混凝土單軸受拉率相關本構方程

(8)

式中：ftd，ft分別為當前應變率及準靜態應變率下抗拉強度；εtfd為當前應變率下受拉峰值應變；E為彈性模量，本文設其與應變率無關。

動態與準靜態抗拉強度關系采用Comité Euro-International du Béton (CEB)[15]模型，即

(9)

(10)

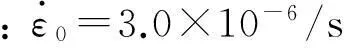
按彈性余能等效原理：在損傷狀態下真實應力與應變對應的彈性余能及未損傷狀態下有效應力與有效應變對應的彈性余能相等，得混凝土拉壓損傷定義為

(11)

式中：Es為拉、壓割線彈性模量；E0為拉、壓初始彈性模量。

用本文試驗所得邊長100 mm混凝土立方體試塊的抗壓強度除以轉換系數1.05，得混凝土立方體(邊長150 mm)抗壓強度fcu。混凝土棱柱體抗壓強度fc計算式為

fc=0.8fcu

(12)

混凝土棱柱體抗拉強度ft計算式為

ft=0.26fcu2/3

(13)

混凝土模型所用材料參數見表2。其中fb0/fc0為雙軸與單軸極限抗壓應力之比；K為拉伸與壓縮子午面第二應力不變量之比，本文取ABAQUS中默認值；aa，ad分別為混凝土單軸抗壓應力應變曲線中上升及下降段參數，可由規范[13]獲得。剪脹角為用于表示材料在剪切過程中體積變化率的物理量，據經驗[9]及本文試驗數據，本文取剪脹角為30。

2.3結果分析

計算獲得鋼筋混凝土梁最大自振頻率為87.079 Hz,遠大于本文加載的最大頻率0.83 Hz，因此可忽略慣性作用對構件受力特性影響。對表1中前8種工況下梁試件進行數值模擬，所得跨中荷載-位移曲線見圖5。由圖5看出，加載速率越大梁的承載力越高；材料強度越低，應變率敏感性越大。不同加載工況下模擬與試驗結果承載力差別不大。加載后期，模擬結果承載力下降偏快。滯回曲線形狀與試驗結果相差較大，模擬曲線較飽滿，而試驗曲線有捏攏現象。主要因計算模型未單獨考慮鋼筋與混凝土間粘結滑移及材料本構模型不夠準確。總體而言，采用本文材料率相關本構模型、計算模型可模擬梁試件在不同加載速率下的主要特征。

表2　混凝土模型的參數

圖5　鋼筋混凝土梁數值模擬結果 Fig.5 Simulated results of reinforced concrete beams

3結論

本文對16根鋼筋混凝土梁在不同加載速率下的受力、變形特性進行試驗研究，考慮材料強度、剪跨比、加載方式及加載速率對鋼筋混凝土梁特性影響，同時基于ABAQUS有限元軟件對8種工況鋼筋混凝土梁的動力特性進行數值模擬，結論如下：

(1)加載速率提高，鋼筋混凝土梁的承載能力亦提高，其大小與梁材料強度、剪跨比及加載方式有關。強度越高承載能力提高的越少。相同材料強度的鋼筋混凝土梁，剪跨比越大承載能力提高越小。梁的材料強度及剪跨比相同時，加載速率提高，循環加載較單調加載時強度提高的少。

(2)試驗中材料應變率效應是快速加載下鋼筋混凝土梁承載力提高的主要原因，慣性作用較小可忽略。

(3)基于ABAQUS有限元軟件建立的計算模型可較好模擬鋼筋混凝土梁的主要動力特性。

參考文獻

[1]林峰,顧祥林,匡昕昕,等.高應變率下建筑鋼筋的本構模型[J].建筑材料學報,2008,11(1):14-20.

LIN Feng, GU Xiang-lin, KUANG Xin-xin, et al.Constitutive models for reinforcing steel bars under high strain rates[J] Journal of Building Materials, 2008,11(1):14-20.

[2]梁磊，顧強康，原璐.AFRP約束混凝土多次沖擊試驗研究[J].振動與沖擊,2013,32(5):90-95.

LIANG Lei, GU Qiang-kang, YUAN lu. Experimental research on AFRP confined concrete under repeated impact [J]. Journal of Vibration and Shock,2013,32(5):90-95.

[3]Bertero V V，Rea D, Mahin S, et al.Rate of loading effects on uncracked and repaired reinforced concrete members[C]. Proceeding of Fifth World Conference on Earthquake Engineering, Rome,1973(1):1461-1471.

[4]Kulkarni S M, Shah S P. Response of reinforced concrete beams at high strain rates[J].ACI Structural Journal, 1998, 95(6): 705-715.

[5]Fu H C, Erki M A, Seckin M. Review of effects of loading rate on reinforced concrete[J]. Journal of Structural Engineering, 1991,117(12):3660-3679.

[6]Pankaj P, Lin E. Material modeling in the seismic response analysis for the design of RC framed structures[J].Engineering Structures,2005,27:1014-1023.

[7]閻石,張亮,王丹.鋼筋混凝土板在爆炸荷載作用下的破壞模式分析[J].沈陽建筑大學學報,2005,21(3):177-180.

YAN Shi, ZHANG Liang, WANG Dan.Failure mode analysis for rc slab under explosive loads[J]. Journal of Shenyang Architectural and Civil Engineering Institute, 2005,21(3): 177-180.

[8]Wei J, Quintero R, Galati N, et al.Failure modeling of bridge components subjected to blast loading. part1:strain rate-dependent damage model for concrete[J]. International Journal of Concrete Structures and Materials, 2007,1(1):19-28.

[9]Chen L,Fang Q, Zhang Y, et al.Rate-sensitive numerical analysis of dynamic responses of arched blast doors subjected to blast loading[J].Transactions of TianJin University,2008,14:348-352.

[10]Shimazaki K, Wada A. Dynamic analysis of a reinforced concrete shear wall with strain rate effect[J].ACI Structural Journal,1998,95(5):488-497.

[11]李敏,李宏男.建筑鋼筋動態試驗及本構模型[J].土木工程學報, 2010,43(4):70-75.

LI Min, LI Hong-nan.Dynamic test and constitutive model for reinforcing steel[J].China Civil Engineering Journal, 2010, 43(4): 70-75.

[12]Lee J, Fenves G L. Plastic-damage model for cyclic loading of concrete structure[J]. Journal of Engineering Mechanics, 1998, 124(8): 892-900.

[13]GB50010-2002,混凝土結構設計規范[S]. 北京：中國建筑工業出版社，2001.

[14]李敏,李宏男,張皓,等.中強混凝土應變率效應的試驗研究與數值模擬[J].混凝土,2014(4):34-37.

LI Min, LI Hong-nan, ZHANG Hao,et al. Experimental and numerical study on the effects of strain rate of middle strength concrete[J].Concrete,2014(4):34-37.

[15]Eibl J. Concrete structures under impact and impulsive loading(CEB-bulletin d’information, NO.187) [R]. Dubrovnik: Comite Euro-International du Beton,1988.