土石壩極限抗震能力的上限有限元法①

土石壩極限抗震能力的上限有限元法①

E-mail: yyfreshman@163.com。

楊昕光1，2， 遲世春3， 饒錫保1， 張偉1， 潘家軍1， 周欣華1， 徐晗1

(1.長江科學院水利部巖土力學與工程重點實驗室，湖北 武漢 430010；

2.水利部土石壩破壞機理與防控技術重點實驗室，江蘇 南京 210029；

3. 大連理工大學海岸與近海工程國家重點實驗室，遼寧 大連 116024)

摘要：基于極限分析上限定理，考慮堆石料內摩擦角較大以及抗剪強度具有非線性的特性，提出一個用于求解土石壩極限抗震能力的有限元計算方法。該方法通過功能平衡條件、位移協調條件、邊界條件、屈服條件以及所求極限荷載，形成標準的二階錐規劃數學模型，并用內點法進行優化迭代求解，得到土石壩坡極限抗震能力的上限值。運用該方法對一個典型面板堆石壩進行抗震極限分析。結果表明：按規范設計的土石壩具有較強的抗震能力，且豎向地震力對大壩的極限抗震能力存在一定影響；此外上限有限元法具有較高的計算精度及工程實用價值。

關鍵詞：土石壩； 極限抗震能力； 極限分析； 上限定理

收稿日期：①2015-04-01

基金項目：國家自然科學基金(51309029)；水利部公益性行業專項(201201039)；水利部土石壩破壞機理與防控技術重點實驗室開放研究基金(YK914017)

作者簡介：楊昕光(1983-)，男，內蒙古赤峰人，博士、工程師，主要從事土石壩地震工程、土工數值計算與分析等方面研究。

中圖分類號:TV641； TV312文獻標志碼：A

DOI:10.3969/j.issn.1000-0844.2015.03.0667

Upper Bound FEM to Analyze the Ultimate Aseismic

Capability of Earth-rock Dams

YANG Xin-guang1, 2, CHI Shi-chun3, RAO Xi-bao1, ZHANG Wei1,

PAN Jia-jun1, ZHOU Xin-hua1, XU Han1

(1.KeyLaboratoryofGeotechnicalMechanicsandEngineeringofMinistryofWaterResources,YangtzeRiverScientificResearch

Institute,Wuhan430010,Hubei，China; 2.KeyLaboratoryofFailureMechanismandSafetyControlTechniques

ofEarth-rockDamoftheMinistryofWaterResources,Nanjing210029,Jiangsu，China;

3.StateKeyLaboratoryofCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian116024,Liaoning，China)

Abstract：An upper bound limit analysis finite element method is developed to study the ultimate aseismic capacity of earth-rock dams. Considering the large value of the internal friction angle and the non-linear shear strength parameters of earth-rock materials, a static form, which is the corresponding dual problem of the second-order cone programming for upper bound limit analysis, is formulated with constraints based on the yield criterion, flow rule, boundary conditions, and the energy-work balance equation. The upper bound solution of ultimate aseismic capacity is then iteratively obtained by a state-of-the-art interior-point algorithm. The proposed method is applied to the seismic stability problem of a typical earth-rock dam. The results indicate that the earth-rock dams designed according to code have strong seismic capabilities, as the influence of vertical earthquake load is considered. These results also demonstrate the high calculation accuracy and practical value of the proposed method.

Key words： earth-rock dam; ultimate aseismic capacity; limit analysis; upper bound theorem

0引言

我國西部地區水力資源豐富，但同時也是地震高烈度區，地震頻發且強度較大。我國已建和在建的土石壩大多位于這一地區。汶川地震發生后，國家加強了水電工程抗震防震工作，規定對特別重要的擋水建筑物，要研究其極限抗震能力和地震破壞模式。

土石壩的極限抗震能力，即為壩坡在地震作用下達到極限狀態時所能承受的地面絕對加速度的最大值。根據現有的研究，壩體滑坡不僅是土石壩常見的震害形式，而且易引起潰壩等嚴重災害，從而危及整個水壩的安全，是大壩極限抗震能力的控制因素[1-3]。因此對土石壩壩坡的極限抗震能力分析是研究的重點問題之一。

極限分析是塑性力學的重要內容，它通過直接分析結構的極限狀態，從上限和下限兩個方向計算與之相對應的極限荷載，不僅與問題的嚴密解大小關系明確，且具有嚴格的理論基礎和物理意義。近年來有些學者[4-6]將有限元法與極限分析方法相結合，通過線數學規劃的方法尋求問題的嚴格上限解和下限解，從而使極限分析方法在求解地基承載力、土坡穩定性等巖土工程領域中得到了廣泛的研究和發展。若將塑性極限分析方法應用于土石壩的抗震分析中，從壩坡穩定的角度求得土石壩的極限抗震能力，不失為解決上述問題的有效途徑。

本文應用上限極限分析有限元方法對土石壩的極限抗震能力進行求解。大量實驗結果[7-9]表明，堆石料的抗剪強度一般與應力相關聯，具有明顯的非線性特性。在以往的塑性極限分析研究中，一般只考慮材料的線性強度，并且為了求解方便，通常將屈服準則表達為線性的形式[4-5]，并利用線性規劃的方法求解極限荷載。這種簡化雖然可以使問題的求解變得簡單、快速，但是由于將屈服準則線性化，使得對于像堆石料這種內摩擦角較大的材料，易產生較大的誤差。此外在上限分析有限元法中，一般采用常應變三角形單元將結構進行離散。Makrodimopoulos等[6]的研究表明，應用六節點三角形高階單元對結構進行離散，假設材料嚴格滿足Mohr-Coulomb屈服準則，并將上限分析形成二階錐規劃進行求解，具有更高的計算精度及求解效率。因此，在此二人的研究基礎之上，本文擬發展土石壩極限抗震能力的上限有限元法，以減小因堆石料內摩擦角較大而引起的計算誤差。同時將上限分析轉化為對偶問題的靜力形式進行求解，以期迭代確定壩體材料的非線性強度參數，進而考慮堆石料的非線性強度特性。

1極限抗震有限元計算方法

1.1極限分析上限定理

塑性極限分析包括兩個方面，即上限定理和下限定理。上限定理從構筑一個塑性區內的允許速度場出發，認定凡是滿足屈服條件及邊界條件下，通過功能平衡條件確定的外荷載一定比真實的極限荷載大。根據Makrodimopoulos和Martin的研究[6]，極限分析上限法可以選用六節點三角形單元，并假設單元之間不存在速度間斷，當結構滿足屈服條件、邊界條件及功能平衡條件時，同樣獲得極為嚴格的上限解。設存在一個完全剛塑性結構V，則根據極限分析上限定理，當結構達到極限狀態時，必定存在一個運動許可速度場u，使得內能耗散不大于外力做功，即：

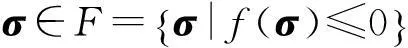
由于假設單元間不存在速度間斷面，所以內能耗散只發生在單元內部。定義內能耗散函數如下：

則式(1)可以寫成：

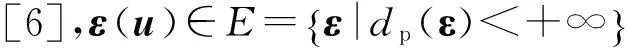
1.2結構的離散

根據Makrodimopoulos和Martin[6]的研究，采用如圖1所示的六節點三角形對結構進行離散，并且假定三角形三個邊均為直邊，且三角形單元之間不存在速度間斷。

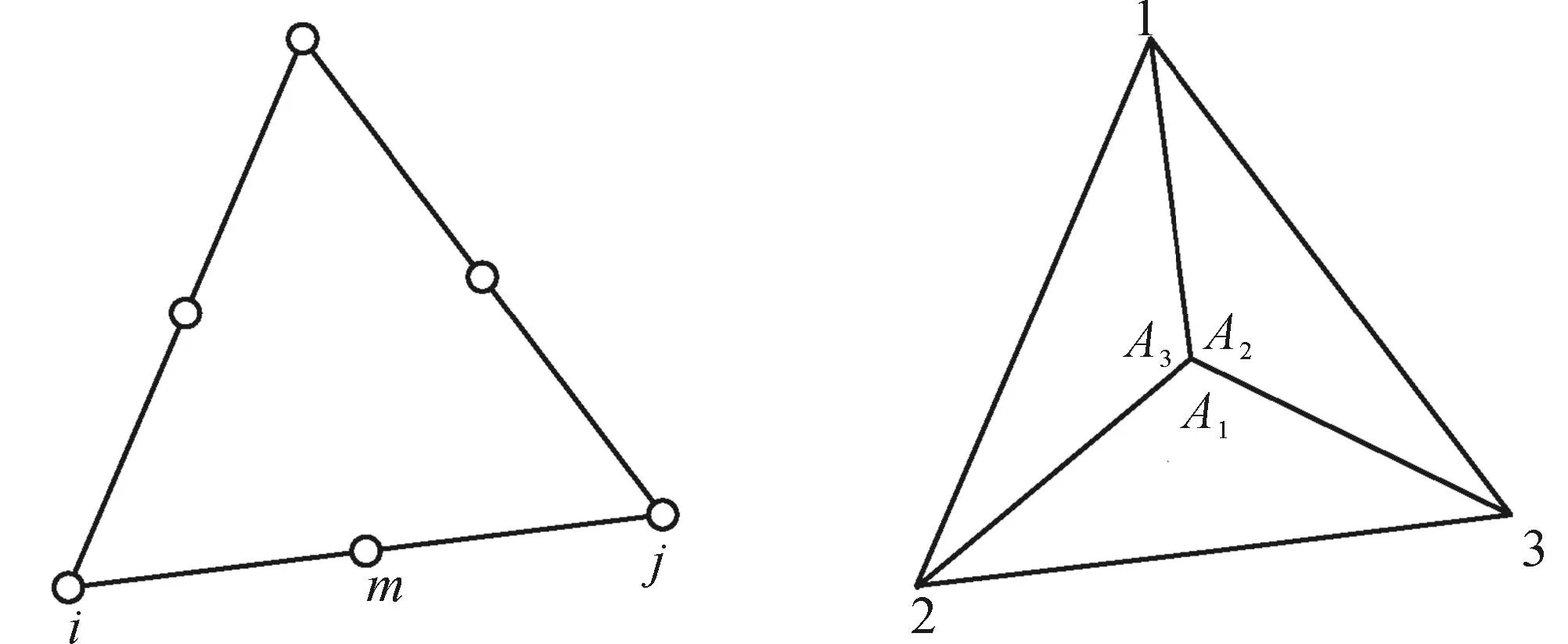
圖1　上限分析的六節點線性應變單元 Fig.1　Six-node linear strain element for upper bound analysis

由于采用的是六節點三角形單元，因此在單元內部的應變分布是線性的。當三角形單元三個邊均為直邊時，單元內的任意一點應變分量可以表示為：

其中：Li=Ai/A為面積坐標；εi為三角形頂點的應變分量(圖1)。由式(5)可知，單元內任意一點的應變均可由三角形三個頂點的應變分量表示。因此，只要三角形三個頂點屬于塑性允許應變場，則單元內任意一點的應變均屬于塑性允許應變場，即ε(u)∈E。由此可知，塑性變量應設置在三角形的三個頂點上。因此，對于六節點三角形單元，除每個節點的速度變量(ui，υi)以外，在三個頂點處還包括塑性變量λi。

1.3屈服準則

在平面應變條件下，Mohr-Coulomb屈服準則可以表示成如下形式：

其中，

式中：δ為Kronecker符號；a、k為材料參數，a=sinφ，k=ccosφ；c、φ分別為材料的黏聚力及內摩擦角。

根據文獻[6]可知，當a≥0時，根據式(2)定義的內能耗散函數可以轉化為以下形式：

其中λ為塑性乘子；θ為體積膨脹系數，即

1.4上限分析的有限元形式

如重力、地震擬靜力荷載以及其他形式的體力、面力均轉化為相應的等效節點荷載，進而計算其所做功。將等效節點荷載分為超載部分q1和非超載部分q0，設超載系數為β，則外力做功Wext可以用下式計算：

則式(4)可以寫成：

其中：ε(u)∈E。

假設一平面應變結構劃分成NE個單元，則根據上限定理以及式(10)及(15)，求超載系數β的上限解，即為求解如下優化問題：

其中：矩陣Bm，i、Bd，i可根據變形協調關系確定，θi=Bm，iu ，[2e112e12]T=Bd，iu。在巖土工程中，位移邊界條件一般為在邊界上滿足u=0，設這一邊界條件已經隱含在式(16)中。根據第二節的分析，為使單元內任意一點均滿足屈服條件，塑性點應設在三角形單元的三個頂點上。由此，如一結構離散成NE個單元，則塑性點個數為NP=3NE個。內能耗散用下式計算：

其中：

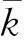
其中：

zi∈為二階錐約束，其中集為：

式中，zi∈即相當于λi≥‖eredi‖。同上，設位移邊界條件為u=0，結構的自由度為NZ，則Bi∈R3×NZ。

由此可知，式(19)是一個標準的二階錐規劃，其對偶形式經過轉換后為：

1.5優化算法

目前，大型稀疏二階錐規劃問題一般均采用內點法求解。內點法具有高效、穩定等優點。實際計算中發現，內點法的迭代次數與問題的規模無關，對于大型問題的求解，一般在迭代20～40次后就能收斂。

在眾多類型內點算法中，原始-對偶內點算法在求解二階錐規劃問題時表現出更好的適應性與求解效率。由Kim-ChuanToh以及MichaelJ.Todd等[11]共同開發的一種基于原始-對偶、路徑跟蹤內點算法是目前最為優秀的優化算法之一。本文即利用該優化算法對二階錐規劃數學模型進行優化求解。

1.6基于材料非線性強度的上限分析

以往極限分析方法應用的前提是材料的強度參數為線性強度。但大量實驗結果表明，堆石料的抗剪強度具有明顯的非線性，在較大應力范圍內τf-σ的關系通常不成直線，而是向下彎曲的曲線。為了更好地反映抗剪強度的非線性，許多學者根據強度試驗結果提出了強度非線性表達式。其中Duncan等[7]在建立雙曲線應力-應變模型時，用對數關系描述強度參數的非線性，即堆石料的內摩擦角服從以下關系：

式中：φ為材料的內摩擦角；φ0為一個大氣壓下的內摩擦角；σ3為小主應力；Δφ為內摩擦角σ3降低的幅度；Pa為大氣壓強。

可見，堆石料的非線性強度參數與應力存在相關性。而極限分析上限定理尋求的是運動許可速度場，并不能直接給出壩體的應力分布情況，從而導致不能準確描述材料強度的非線性特性。為了得到問題精確的上限解，需要已知壩體的應力分布情況。當把上限分析二階錐規劃轉化為其對偶問題的靜力形式進行求解時，就可以通過迭代的方法得到材料的非線性剪切強度參數。結合第5節，基于材料非線性強度的上限分析的一般計算流程為：

(1) 假設各單元的內摩擦角為一初始值φini。

(2) 對每個塑性點進行循環，根據式(21)求解Gm，i，Gd，i，q0，q1等子矩陣。

(3) 把子矩陣按照組合成總體約束矩陣，形成二階錐規劃模型，并對其進行優化求解，得到問題的上限解及靜力形式的應力場。

(4) 根據各單元的應力，通過式(22)求解φ，并設為φsec。

(5) 當99%以上的單元均滿足|φsec-φini|≤ζ，則認為滿足工程精度需求，此時得到的解即為極限分析上限解。否則令φini=φsec，重復步驟(2)～(5)。ζ為精度要求，取任意一小正數。一般迭代幾次即可得到滿意的結果。

(6) 利用互補松弛定理求得原問題的最優解及運動許可速度場u，輸出計算結果。

綜上，基于以上計算原理，采用MATLAB編制了求解土石壩極限抗震能力的上限有限元計算程序。

2算例與分析

采用上述方法對一典型面板堆石壩進行極限抗震能力研究。設大壩壩高100 m，壩頂寬度8 m，上、下游壩坡坡比均為1∶1.4。取堆石料為非線性強度參數，其中γ=20 kN/m3，φ0=52.3°，Δφ=11.0°(取自文獻[9])。

我國《水工建筑物抗震設計規范》[12]規定采用擬靜力法進行土石壩抗震穩定分析，即將地震力看成類似于重力的靜荷載施加在結構上，并考慮土石壩地震加速度反應沿壩高呈上大下小分布這一實際情況，用壩體動態分布系數αi來反映這一調整的概念。

因此，作用在單元體上的水平地震力的計算公式為：

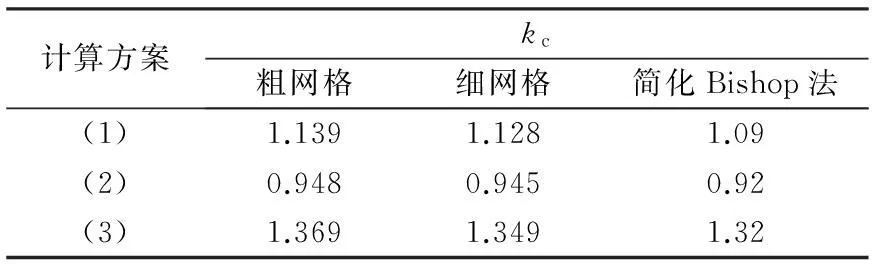
式中:αi為動態分布系數，根據規范按不同高度進行選取；ξ為地震作用效應的折減系數，一般情況下取為0.25；W為土體單元的重力；kh為地震加速度系數，是地面水平最大加速度αh與重力加速度g的比值：kh=ah/g。為了考慮豎向地震力對大壩極限抗震能力的影響，計算中采取以下三種方案：(1)僅考慮水平向地震慣性力；(2)同時考慮水平、豎直向地震慣性力，且豎直向地震慣性力方向為豎直向上；(3)同時考慮水平、豎直向地震慣性力，且豎直向地震慣性力方向為豎直向下。其中豎向地震力的大小可近似地取水平向地震力的2/3。為了考慮有限元網格尺寸對上限有限元極限分析計算結果的影響，分別以粗網格、細網格為例進行計算分析，并與簡化Bishop法的結果進行對比。其中，粗網格共剖分800個單元，1 681個結點；細網格共剖分5 000個單元，10 201個結點。細網格有限元剖分圖見圖2。

圖2　堆石壩有限元剖分圖(細網格) Fig.2　 Finite element mesh of the rockfill dam(fine mesh)

計算方案kc粗網格細網格簡化Bishop法(1)1.1391.1281.09(2)0.9480.9450.92(3)1.3691.3491.32

由計算結果可知，豎向地震力對大壩極限抗震存在一定影響。同時，隨著單元網格密度的增加，大壩極限抗震能力的上限解略有降低。對于三種不同計算方案，細網格條件下的計算結果比粗網格下的結果平均降低了1.7%，說明上限有限元法的計算結果并不明顯依賴于網格的密度。圖3為壩坡處于極限狀態時的位移矢量圖，由此可以確定壩坡最危險滑動面的位置和形狀。與簡化Bishop法的計算結果比較可知，無論是大壩極限抗震能力還是最危險滑動面，其他兩種方法均具有較好的一致性。但由于本文方法所得結果是極限抗震能力的上限值，因此比極限平衡法的計算結果略大。

圖3　大壩處于極限狀態時的位移矢量圖 Fig.3　Displacement vector map for the dam in limit state

3結論與展望

本文基于極限分析上限定理，提出了一個用于求解土石壩極限抗震能力的有限元計算方法，并通過實際工程算例分析得到如下主要結論：

(1) 由于借助極限分析上限定理及有限元技術，并在計算中考慮了堆石料強度的非線性特性，使本文所提上限有限元法在土石壩極限抗震能力分析中具有較高的計算精度及較強的適應性。

(2) 算例分析表明，豎向地震力對大壩極限抗震能力存在一定影響。此外，通過大壩位移矢量圖可確定最危險滑動面的位置和形狀，符合土石壩在地震作用下的一般破壞規律。

(3) 與極限平衡法計算結果對比可知，兩種方法具有較好的一致性。

(4) 由于有限元極限分析方法不需要預先對滑動破壞模式進行假定，且在復雜計算條件下具有較強的適應能力，因此可將該方法擴展至三維條件下的土石壩極限抗震能力分析。

參考文獻(References)

[1] 趙劍明，劉小生，陳寧，等. 高心墻堆石壩的極限抗震能力研究[J].水力發電學報，2009，28(5)：97-102.

ZHAO Jian-ming,LIU Xiao-sheng,CHEN Ning,et al.Research on the Maximum Anti-seismic Capability of High Earth Core Rock-fill Dam[J].Journal of Hydroelectric Engineering,2009,28(5): 97-102. (in Chinese)

[2] 李國英，沈婷，趙魁芝.高心墻堆石壩地震動力特性及抗震極限分析[J].水利水運工程學報，2010(1)：1-8.

LI Guo-ying,SHEN Ting,ZHAO Kui-zhi.Seismic Dynamic Behavior and Limit Aseismic Analysis on High Earth Core Rockfill Dams[J].Hydro-science and Engineering,2010(1):1-8.(in Chinese)

[3] 陳生水，李國英，傅中志.高土石壩地震安全控制標準與極限抗震能力研究[J].巖土工程學報，2013，35(1)：59-65.

CHEN Sheng-shui,LI Guo-ying,FU Zhong-zhi.Safety Criteria and Limit Resistance Capacity of High Earth-rock Dams Subjected to Earthquakes[J].Chinese Journal of Geotechnical Engineering, 2013,35(1):59-65.(in Chinese)

[4] Sloan S W.Lower Bound Limit Analysis Using Finite Elements and Linear Programming[J].International Journal Analytical Method in Geomechanics，1988，12(1)：61-77.

[5] Sloan S W.Upper Bound Limit Analysis using Finite Elements and Linear Programming[J].International Journal Analytical Method in Geomechanics，1989，13(3)：263-282.

[6] Makrodimopoulos A，Martin C M.Upper Bound Limit Analysis Using Simplex Strain Elements and Second-order Cone Programming[J].International Journal for Numerical and Analytical Methods in Geomechanics，2007，31(6)：835-865.

[7] Duncan J M，Byrne P M，Wong K S.Strength，Stress-strain and Bulk Modulus Parameters for Finite Element Analysis of Stress and Movements in Soil Masses[R].Berkeley： Berkeley University of California，1980.

[8] Indraratna B，Wijewardena L S S，Balasubramaniam A S.Large-scale Triaxial Testing of Greywacke Rockfill[J].Géotechnique，1993，43(1)：37-51.

[9] 陳立宏，陳祖煜.堆石非線性強度特性對高土石壩穩定性的影響[J].巖土力學，2007，28(9)：1807-1810.

CHEN Li-hong, CHEN Zu-yu. Effect of Nonlinear Strength of Rockfill on Slope Stability of High Earth-rock Dam[J].Rock and Soil Mechanics,2007,28(9):1807-1810.(in Chinese)

[10] Michalowski R L.Slope Stability Analysis：a Kinematical Approach[J].Géotechnique，1995，45(2)：283-293.

[11] Tütüncü R H，Toh K C，Todd M J.Solving Semidefinite-quadratic-linear Programs Using SDPT3[J].Mathematical Programming，2003，95(2)：189-217.

[12]DL5073-2000,水工建筑物抗震設計規范[S].北京: 中國電力出版社，2000.

DL5073-2000,Specifications for Seismic Design of Hydraulic Structures[S].Beijing:China Electric Power Press,2000.(in Chinese)