基于Gassmann方程的流體替換方法在珊溪水庫地震研究中的應(yīng)用①

基于Gassmann方程的流體替換方法在珊溪水庫地震研究中的應(yīng)用①

鐘羽云, 張帆, 闞寶祥

(浙江省地震局，浙江 杭州 310013)

摘要：引入基于Gassmann方程的流體替換方法，在分析地震波P波速度、波速比與巖石孔隙度和飽和度關(guān)系的基礎(chǔ)上，應(yīng)用于珊溪水庫地震波速比和P波速度變化特征研究，得到：(1)珊溪水庫震中區(qū)巖石始終處于接近水飽和的飽水狀態(tài)，波速比和P波速度“下降-回升”的變化實(shí)質(zhì)上反映了震中區(qū)巖石“孔隙度增大(飽和度減小)-飽和度增大”的變化，每一叢地震的波速比由極小值逐漸增大為極大值是由于巖石從不飽和狀態(tài)變化到飽和狀態(tài)；(2)根據(jù)每一叢地震波速比的變化，計(jì)算得到珊溪水庫流體擴(kuò)散率αs=1.06×104 cm2 s-1，該數(shù)值與美國南卡羅萊納水庫、巴西Acu水庫、廣東新豐江水庫的流體擴(kuò)散率基本一致；(3)震源區(qū)巖石孔隙度上限值為8.7%～2.0%，該數(shù)值與華東勘測設(shè)計(jì)研究院通過室內(nèi)巖石物理力學(xué)性質(zhì)試驗(yàn)測定的珊溪水庫壩址區(qū)新鮮流紋斑巖的孔隙度平均值一致。

關(guān)鍵詞：Gassmann方程； 孔隙度； 飽和度； 珊溪水庫

收稿日期：①2014-12-25

基金項(xiàng)目：浙江省公益技術(shù)應(yīng)用研究項(xiàng)目(2012C23035)

作者簡介：鐘羽云(1966-)，男，碩士，研究員，主要從事地震預(yù)測方法、水庫地震等研究。 E-mail:hzyuyun@126.com。

中圖分類號(hào):P631.4文獻(xiàn)標(biāo)志碼：A

DOI:10.3969/j.issn.1000-0844.2015.03.0678

Application of Gassmann Equation-based Fluid Substitution

Method to the Research of Reservoir-induced

Earthquakes at Shanxi Reservoir

ZHONG Yu-yun, ZHANG Fan, KAN Bao-xiang

(EarthquakeAdministrationofZhejiangProvince,Hangzhou310013,Zhejiang，China)

Abstract：By analyzing the relationship between seismic P-wave velocity, velocity ratio, and rock porosity and saturation in the Shanxi reservoir, the fluid substitution equation method based on the Gassmann equation was used to estimate the rock porosity and fluid diffusion rate in the reservoir’s earthquake source region. The results show that the rock of the epicentral area is always close to the water-saturated state. The changes in P-wave velocity and the velocity ratio from decreasing to increasing reflect that the rock in the epicentral area changes from increasing porosity (decreasing saturation) to increasing saturation. The velocity ratio gradually increases from the minimum value to the maximum value because of the changes in rock conditions from unsaturated to saturated. Moreover, the fluid diffusivity of the Shanxi reservoir is 1.44 × 104 cm2 s-1 to 0.84 × 104 cm2 s-1, which is consistent with that of the South Carolina reservoir in the United States, the Acu reservoir in Brazil, and the Xinfengjiang reservoir in Guangdong, China. Further, the maximum rock porosity in the source area is 8.7%～2.0%, which is consistent with the average value of porosity of new rhyolite porphyries in the Shanxi reservoir dam site measured by the East China Investigation and Design Institute by lab testing of the physical and mechanical properties of the rock.

Key words： Gassmann equation; porosity; saturation; Shanxi reservoir

0引言

水庫地震誘發(fā)機(jī)理研究表明，水庫蓄水后將導(dǎo)致庫水向下滲透，改變庫基巖體的應(yīng)力狀態(tài)和介質(zhì)性質(zhì)，誘發(fā)地震活動(dòng)。因此水庫地震與庫水向地下滲透運(yùn)移有著不可分割的聯(lián)系[1-2]，水在水庫誘發(fā)地震中起著重要作用。由于水的作用，介質(zhì)的物理性狀將產(chǎn)生一系列變化，如出現(xiàn)微破裂、擴(kuò)容、塑性硬化及相變等。地震波通過地殼介質(zhì)時(shí)，地震波速、波速比、地震波Q值等與震源區(qū)介質(zhì)有關(guān)的參數(shù)均將發(fā)生變化。近幾年來，有關(guān)水庫區(qū)域地震波速異常、波速比異常、地震波Q值變化的震例越來越多[3-7]。巖石力學(xué)實(shí)驗(yàn)也表明，巖石中流體的存在將會(huì)影響巖石介質(zhì)的地震波傳播特性。例如，施行覺等[8]通過實(shí)驗(yàn)測量和理論計(jì)算認(rèn)為當(dāng)飽和度高于某值時(shí)，含水量的增加可使縱波波速增加30%左右。史謌等[9]實(shí)驗(yàn)表明，地震波速度不僅與巖石飽和度有關(guān)，還與不同飽和階段的孔隙流體分布有關(guān)，并且進(jìn)水和失水過程中縱、橫波速度與飽和度關(guān)系顯示出不同規(guī)律。

地震巖石物理學(xué)研究表明，巖石的壓力、溫度、飽和度、流體類型、孔隙度、孔隙類型等因素都將影響到巖石的地震特性(密度、速度、體積模量等)，即當(dāng)這些因素中的一個(gè)或多個(gè)發(fā)生變化時(shí)，巖石的地震特性也將隨之發(fā)生變化[10]。巖石物理研究的主要方法是通過一定的假設(shè)條件把實(shí)際的巖石理想化，通過內(nèi)在的物理學(xué)原理建立理論模型。經(jīng)過幾十年的發(fā)展，根據(jù)不同的假設(shè)條件，科學(xué)家們提出了不同的巖石物理理論模型[10]。Gassmann建立了反映地震波速度、介質(zhì)孔隙度以及孔隙流體模量相互關(guān)系的Gassmann方程[11]，成為巖石物理理論模型建立的里程碑。該模型屬于球形孔隙模型，即假設(shè)巖石是由顆粒和球狀孔隙組成的集合體。近年來，巖石物理技術(shù)廣泛用于估算巖石的孔隙度和飽和度，預(yù)測儲(chǔ)層條件下油氣層的縱、橫波速度等，在油田勘探開發(fā)中發(fā)揮了重要作用[12]。

本文首先從Gassmann方程出發(fā)，分析地震波P波速度、波速比分別與巖石孔隙度和飽和度的關(guān)系；其次分別使用重復(fù)地震方法、和達(dá)法計(jì)算珊溪水庫地震P波速度和波速比的變化，給出水庫地震波速異常的物理解釋，估算珊溪水庫流體擴(kuò)散率和震源區(qū)巖石孔隙度；最后探討珊溪水庫誘發(fā)地震的機(jī)理。

1Gassmann方程和流體替換

Gassmann假設(shè)：(1)巖石(固體和骨架)宏觀上是均勻的；(2)所有空隙都是連通的；(3)所有空隙都充滿流體；(4)研究中的巖石-流體系統(tǒng)是封閉的；(5)孔隙流體不對(duì)固體骨架產(chǎn)生軟化或硬化相互作用等條件下，推導(dǎo)出Gassmann方程[11]。

式(1)中，k是以有效體積模量為kf的孔隙流體所飽和巖石的有效體積模量；kb是干巖石(骨架) 有效體積模量；ks是基質(zhì)礦物(顆粒)體積模量；φ是孔隙度；kf為孔隙流體體積模量。式(2)、(3)中，vP為縱波速度;vS為橫波速度;μb為巖石剪切模量;ρ為巖石的等效密度。式(4)、(5)中，ρs為巖石基質(zhì)密度;ρf為孔隙流體密度;ρw為地層水的密度;ρg為氣體密度;sw為含水飽和度。

在剪切模量保持一致的條件下，利用式(2)、(3)可以求取縱波速度和橫波速度。

2地震波速度、波速比與巖石孔隙度和飽和度的關(guān)系

利用Gassmann方程進(jìn)行波速計(jì)算時(shí)，需先確定方程組中的各項(xiàng)參數(shù)。各參數(shù)確定方法為：

(1) 巖石基質(zhì)模量與密度的確定

當(dāng)已知巖石的礦物組成和各種礦物組成的百分含量以及相應(yīng)彈性模量和密度時(shí)，利用Vogit-Russ-Hill平均方法可確定基質(zhì)的彈性模量，利用加權(quán)算術(shù)平均即可確定基質(zhì)的密度[10，13]。馬中高[14]通過砂巖樣品試驗(yàn)測試結(jié)果，得到干燥巖石體積模量與孔隙度間關(guān)系：

式中，n的取值范圍為0～1;ks、kf、φ含義與前面相同；φc為臨界孔隙度。

珊溪水庫庫區(qū)在太古代的結(jié)晶基底上沉積了巨厚的中生代火山碎屑及河湖相沉積，庫區(qū)巖性主要為侏羅系上統(tǒng)火山碎屑巖和白堊系下統(tǒng)河湖相沉積巖夾火山巖[15]。華東勘測設(shè)計(jì)研究院在工程地質(zhì)勘測中通過室內(nèi)巖石物理力學(xué)性質(zhì)試驗(yàn)，得到珊溪水庫壩址區(qū)侏羅系上統(tǒng)磨石山群d段新鮮流紋斑巖比重平均值為2.64 g/cm3，干巖石抗壓強(qiáng)度平均值為207.00 MPa，孔隙度平均值為3.41%。通過現(xiàn)場巖體彈性波(地震法)測試，得到新鮮流紋斑巖的動(dòng)泊松比為0.22～0.28*華東勘測設(shè)計(jì)研究院.浙江省飛云江珊溪水庫工程可行性研究工程地質(zhì)勘察報(bào)告.1994.。劉素梅等[16]根據(jù)丹江口水庫庫區(qū)6種巖樣在干燥狀態(tài)下共108個(gè)試件的實(shí)測數(shù)據(jù)，通過擬合得到彈性模量E和抗壓強(qiáng)度R之間的關(guān)系為：

R=0.004 3E+31.949

根據(jù)華東勘測設(shè)計(jì)研究院對(duì)珊溪水庫壩址區(qū)的測試結(jié)果，取ρs=2.64 g/cm3，干巖石抗壓強(qiáng)度R=207.00 MPa，泊松比ν=0.26；參考馬中高[14]的砂巖樣品試驗(yàn)研究結(jié)果，取n=2/3，φc=0.5;然后通過式(6)、(7)、(8)計(jì)算得到μ=16.2 GPa，ks=30.5 GPa。

(2) 孔隙流體特性的計(jì)算

在Gassmann方程中，孔隙流體的影響是通過孔隙流體體積模量kf體現(xiàn)出來的。當(dāng)其為多種流體的混合物時(shí)，kf可利用著名的Wood方程，由構(gòu)成混合物的各種流體的體積模量與相應(yīng)的體積百分比計(jì)算得到。水庫區(qū)巖石孔隙內(nèi)的流體主要為氣、水混合物，其體積模量kf可由下式給出。

式中各符號(hào)的含義與前面相同。

確定式(1)、(2)、(3)中的各項(xiàng)參數(shù)后，就可以根據(jù)式(2)和式(3)計(jì)算出地震波縱、橫波速度，進(jìn)而計(jì)算出地震波波速比。式(1)表明，巖石的有效體積模量與巖石基質(zhì)體積模量、干巖石體積模量、巖石孔隙度、飽和度有關(guān)。巖石基質(zhì)體積模量與組成巖石各礦物組分的體積模量有關(guān)，對(duì)于某一特定區(qū)域來說巖石基質(zhì)體積模量不隨時(shí)間變化。因此，巖石的有效體積模量主要與孔隙度和飽和度有關(guān)。本文主要研究巖石縱波速度、波速比(vP/vS)與巖石孔隙度和飽和度的關(guān)系。圖1給出了水飽和度一定時(shí)波速比和P波速度隨孔隙度的變化曲線。曲線顯示，隨著孔隙度增大，波速比和P波速度均逐漸變小。

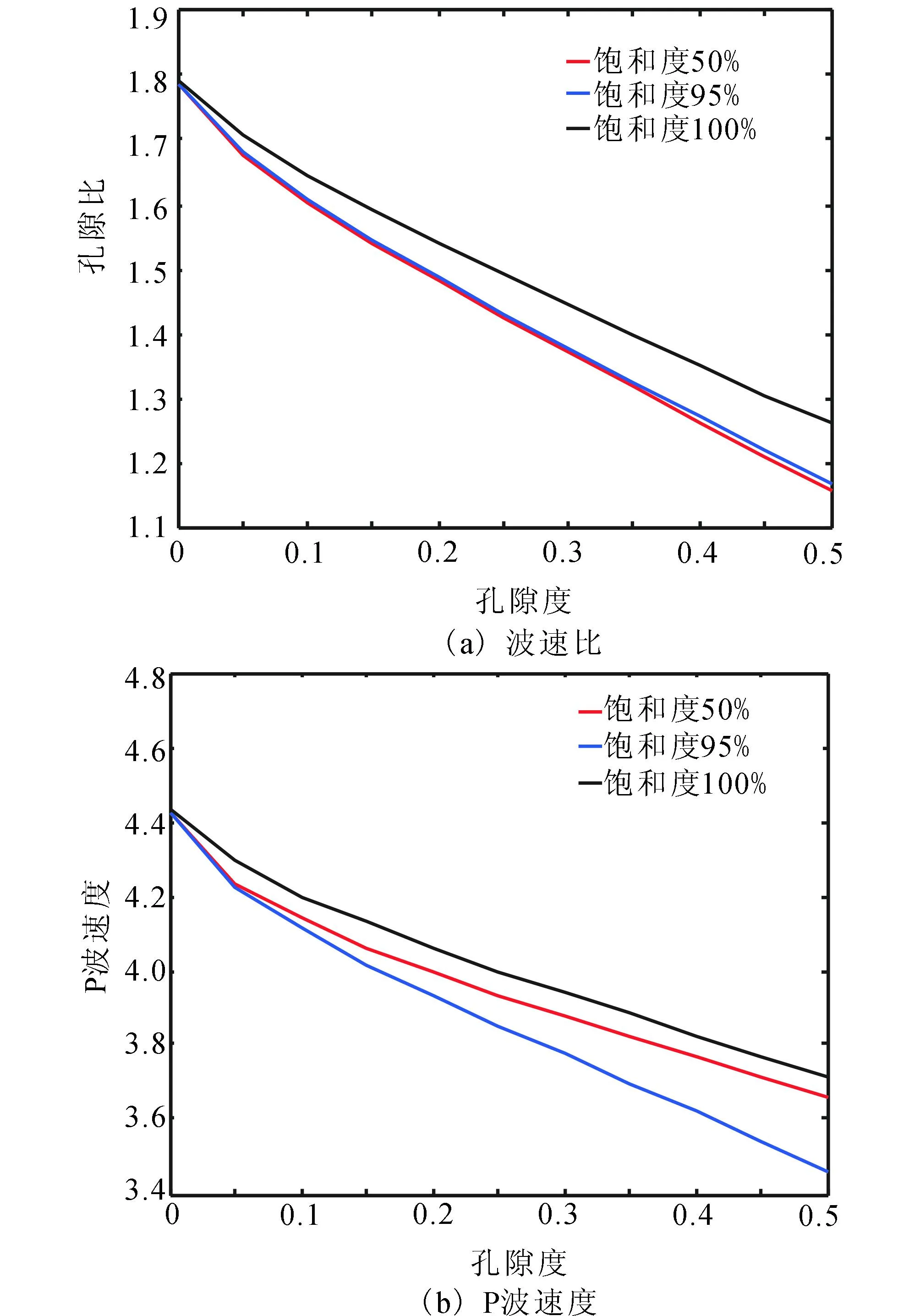
圖1　飽和度一定時(shí)波速比及P波速度隨孔隙度的變化 Fig.1　Wave velocity ratio and P wave velocity change 　　　with the porosity when the saturation is constant

圖2(a)給出了孔隙度一定時(shí)波速比隨水飽和度的變化曲線。曲線顯示，當(dāng)飽和度較小時(shí)(約小于95%)，飽和度的變化對(duì)波速比的影響很小;當(dāng)巖石接近飽和時(shí)(約大于95%)，波速比隨著飽和度增大迅速增大。圖2(b)給出了孔隙度一定時(shí)P波速度隨水飽和度的變化曲線，曲線的變化趨勢(shì)不是單調(diào)的，隨著巖石的飽和度增大P波速度先減小而后增大。

圖2　孔隙度一定時(shí)波速比和P波速度隨飽和度的變化 Fig.2　Wave velocity ratio and P wave velocity change with 　　　 the saturation when the porosity is constant

巖石所處的飽水狀態(tài)不同，波速比和P波速度隨飽和度的變化趨勢(shì)也不同。當(dāng)巖石接近飽和時(shí)(如飽和度大于90%)，波速比和P波速度均隨飽和度的增加而迅速增大;當(dāng)巖石飽和度較小時(shí)(如飽和度小于90%)，波速比隨飽和度增加而增大，P波速度隨著飽和度的增加而減小，兩者的變化趨勢(shì)不同(表1)。因此，可以根據(jù)波速比、P波速度隨水飽和度的變化趨勢(shì)是否相同，判定巖石的飽水狀態(tài)。

如果已知波速比，根據(jù)式(1)、(2)、(3)可以得到某一飽和度下的孔隙度，也可以得到某一孔隙度下的飽和度，并在一定的假設(shè)條件下計(jì)算和分析震源區(qū)巖石的滲透和孔隙變化。

表 1　P波速度、波速比的影響因素

3珊溪水庫地震波速比與P波速度

珊溪水庫于2000年5月下閘蓄水，2002年7月開始發(fā)生地震，其地震具有成叢、成組分布的特點(diǎn)(圖3)。對(duì)地震進(jìn)行重新定位后顯示[15,17]:2002年地震主要發(fā)生在水庫淹沒區(qū)，震中比較集中(圖4);2004—2005年地震開始向水庫南岸遷移，震中變得分散;2006年后地震震中的優(yōu)勢(shì)分布方向?yàn)镹W，與穿過水庫區(qū)的一條NW向斷層走向一致[18]。

3.1地震波速比

上世紀(jì)50年代初已開展了波速比方面的研究，共計(jì)算方法已經(jīng)非常成熟。采用多臺(tái)和達(dá)法計(jì)算珊溪水庫地震波速比[19]，即根據(jù)P波走時(shí)和P、S波到時(shí)差的線性關(guān)系得到vP/vS波速比值、線性相關(guān)系數(shù)R和波速比的計(jì)算誤差γ:

圖3　珊溪水庫地震分布 Fig.3　Earthquake distribution in Shanxi reservoir area

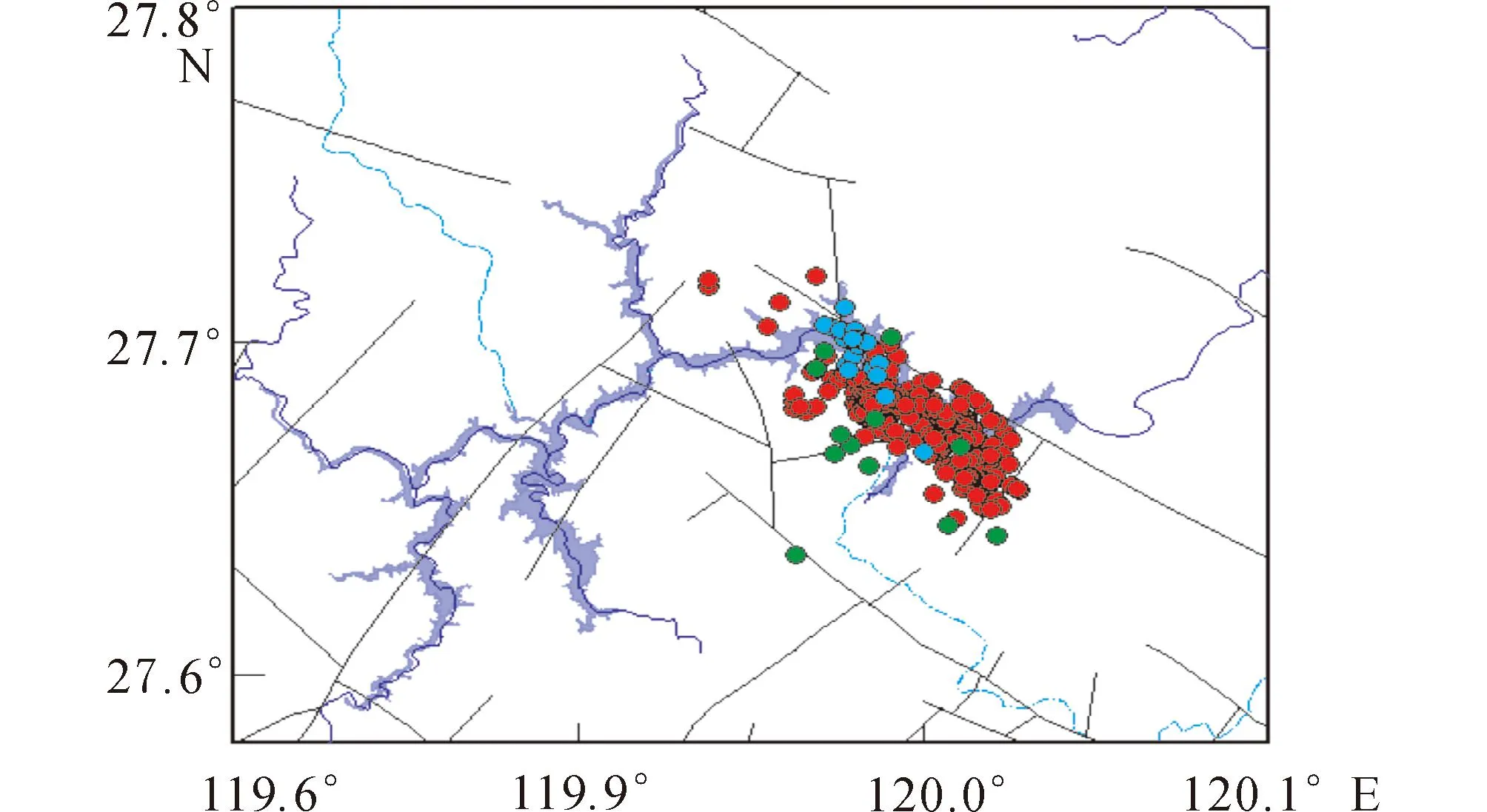
圖4　珊溪水庫震中分布(藍(lán)：2002—2003年； 　　　綠：2004—2005年；紅：2006年以后) Fig.4　Epicenter distribution in Shanxi reservoir area (blue: 　　　 2002— 2003;green:2004 —2005;red:after 2006)

式(10)、(11)、(12)中，tPi為P波走時(shí);tSi為S波走時(shí);Δti=tSi-tPi；n為每個(gè)地震到時(shí)數(shù)據(jù)個(gè)數(shù)；γ為波速比的計(jì)算誤差；δtPi=(tPi-t0 )-Δti(vP/vS-1)[9]。

地震波速比計(jì)算的關(guān)鍵是震相判讀的精度和可靠性，影響波速比計(jì)算精度的主要因素有：直達(dá)P波和S波的到時(shí)判讀精度、參與擬合的臺(tái)站個(gè)數(shù)、地震定位精度等。為了將上述因素的影響盡可能降低到最小，選擇P、S波到時(shí)差△t≤14 s的臺(tái)站數(shù)據(jù)，即距離震中約小于120 km的臺(tái)站直達(dá)波到時(shí)資料進(jìn)行計(jì)算。珊溪水庫地震集中分布在一個(gè)由NW走向和NE走向斷裂圍限的小菱形塊體(約6 km×8 km)內(nèi)[20]。由于震中非常集中，減少了地震分布過于分散而導(dǎo)致路徑差異增大的影響，提高了波速比計(jì)算的穩(wěn)定性。珊溪水庫地震震中120 km范圍內(nèi)有18個(gè)臺(tái)站，震中20 km范圍內(nèi)有7個(gè)臺(tái)站。參與計(jì)算每次地震波速比的臺(tái)站到時(shí)數(shù)據(jù)(一律采用Pg和Sg震相數(shù)據(jù))至少在4個(gè)臺(tái)站以上的數(shù)據(jù)，最多達(dá)到18個(gè)臺(tái)站數(shù)據(jù)。地震震相的判讀精度將直接反映在相關(guān)系數(shù)和計(jì)算誤差中，如果震相的判讀精度較低，則將導(dǎo)致波速比計(jì)算誤差過大，淹沒波速比的異常信息。本文使用重新定位后的發(fā)震時(shí)刻數(shù)據(jù)進(jìn)行波速比計(jì)算，選取相關(guān)系數(shù)R≥0.95,計(jì)算誤差γ≤0.085(即大于5%的波速比異常是可信的)的結(jié)果，得到768次地震波速比計(jì)算結(jié)果。珊溪水庫90%的地震波速比集中分布在1.66～1.75，波速比平均值為1.70(圖5(a)),并隨時(shí)間經(jīng)歷了多個(gè)“下降-回升”的變化過程(圖5(b))。

圖5　珊溪水庫波速比分布及波速比隨時(shí)間變化 Fig.5　Wave velocity ratio distribution and wave velocity ratio changes over time in Shanxi reservoir area

3.2地震P波速度變化

采用同一臺(tái)站記錄的重復(fù)地震的P波走時(shí)變化來研究P波速度變化。由于天然重復(fù)地震并不是完全意義上的重復(fù)，震源之間存在一定的位置差異，因此同一臺(tái)站接受重復(fù)地震時(shí)具有射線路徑偏移，從而引起走時(shí)差變化。周龍泉等[21]提出采用射線追蹤技術(shù)以及波形互相關(guān)方法來消除由于射線路徑不同以及走時(shí)讀取引起的誤差。對(duì)于一叢重復(fù)地震，地震事件1、2在同一臺(tái)站的P波走時(shí)差δt主要受地震的相對(duì)位置、P波到時(shí)讀取精度、地震波傳播路徑介質(zhì)物性變化、地震定位精度等因素的影響。由于地殼介質(zhì)物性的變化，同一個(gè)臺(tái)站接收到不同時(shí)期的重復(fù)地震，其走時(shí)具有差異。重復(fù)地震之間的走時(shí)差可以寫成：

式中，δt表示由于地震和臺(tái)站之間射線路徑上的介質(zhì)變化引起的走時(shí)差；Δt表示兩個(gè)重復(fù)地震在同一臺(tái)站的觀測走時(shí)差；Δt1 表示由于重復(fù)地震位置差異導(dǎo)致的射線路徑不同引起的走時(shí)差；Δt2表示由于走時(shí)讀取誤差引起的走時(shí)差；ε表示現(xiàn)有地震定位條件下的定位誤差。

珊溪水庫地震全部為數(shù)字地震記錄，通過剔除震相不清晰地震事件、重新校核走時(shí)等工作，可以減小走時(shí)讀取誤差引起的走時(shí)差Δt2，使數(shù)字化波形走時(shí)誤差在0.02 s左右。對(duì)于一個(gè)重復(fù)地震序列，選取第一個(gè)重復(fù)地震作為參考地震，將研究區(qū)域的速度結(jié)構(gòu)模型視為介質(zhì)未擾動(dòng)時(shí)的速度模型，通過射線追蹤計(jì)算所有地震到達(dá)同一臺(tái)站的理論走時(shí)，然后將該理論走時(shí)減去參考地震到達(dá)臺(tái)站的理論走時(shí)，就可以消除由于地震位置不同引起的走時(shí)差Δt1。如果不考慮定位誤差，根據(jù)式(13)消除射線路徑不同引起的走時(shí)差Δt1和走時(shí)讀取誤差引起的走時(shí)差Δt2后，就可以得到由地殼介質(zhì)變化引起的實(shí)際走時(shí)差。計(jì)算所有重復(fù)地震相對(duì)參考地震的走時(shí)差，可以得到P波走時(shí)差隨時(shí)間變化的特征，分析P波速度隨時(shí)間的變化。

2002年7月珊溪水庫發(fā)生地震時(shí)，水庫區(qū)沒有地震臺(tái)，距離震中區(qū)最近的溫州地震臺(tái)距震中約73 km。珊溪水庫地震震中位置集中(圖4)，選取2002年7月28日ML3.5地震為參考地震，選擇屯溪—溫州剖面地殼速度模型[22]，計(jì)算參考地震5 km半徑范圍內(nèi)所有地震與參考地震的走時(shí)差(圖6)。P波走時(shí)差的變化反映了P波速度的變化，即走時(shí)差增大、速度減小，走時(shí)差減小、速度增大。圖6顯示，溫州臺(tái)P波走時(shí)差經(jīng)歷了多個(gè)“增大-減小”的變化過程，即P波速度經(jīng)歷了多個(gè)“減小-增大”的變化過程。

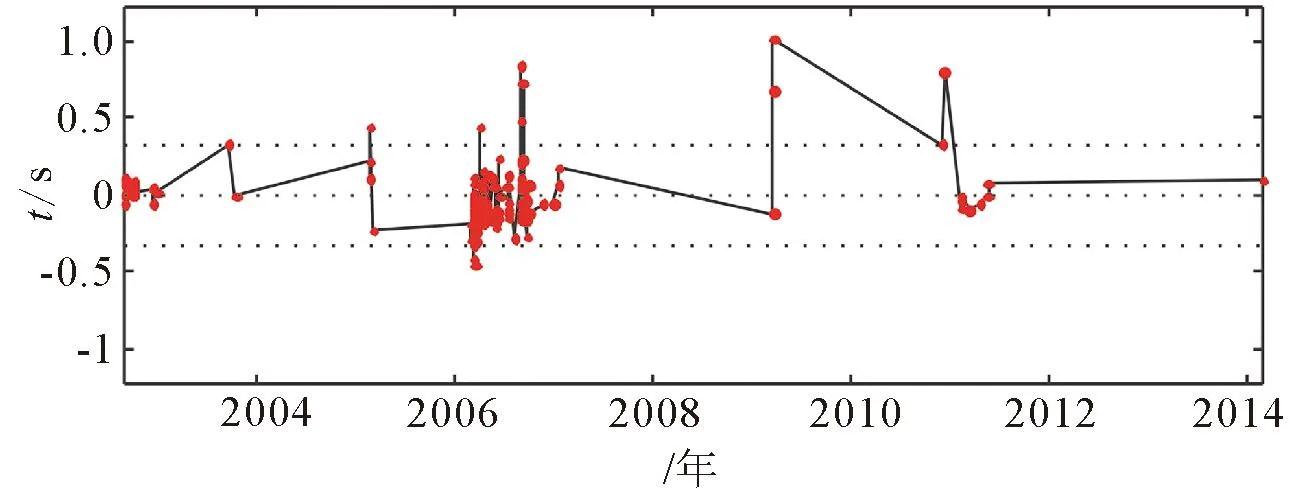
圖6　珊溪水庫地震在溫州臺(tái)的P波走時(shí)差變化 Fig.6　Variation of P wave’s travel time of Shanxi reservoir 　　　 earthquake at in Wenzhou station

3.3波速比與P波速度變化特征

珊溪水庫地震波速比與P波速度具有相似的變化特征，且與地震時(shí)空分布的階段性特征有一定關(guān)系。例如，2002—2003年震中主要位于水庫淹沒區(qū)，這一叢地震的波速比和P波速度經(jīng)歷了一個(gè)“快速下降-緩慢回升”的過程:至2002年8月30日ML2.6地震的波速比下降為這一叢的極小值1.66后，波速比逐漸增大，到2003年8月21日ML1.8地震的波速比增大到這一叢的極大值1.74。此次地震至2005年的一叢地震震中開始向水庫南岸遷移，相應(yīng)的波速比和P波速度經(jīng)歷了“緩慢下降-快速回升”的變化過程。圖5(b)和圖6還顯示，每一叢地震發(fā)生初期波速比和P波速度較大，隨后有一個(gè)逐漸減小的過程，例如，2002年、2006年發(fā)生兩叢地震，其波速比均有一個(gè)逐漸變小的過程。

一次地震就是一次巖體破裂或一次原有斷裂的重新活動(dòng)。小震的發(fā)生形成了良好的滲水通道，導(dǎo)致庫水滲入較深部位或在周邊其他地方引發(fā)后續(xù)地震。按照地震的時(shí)空分布，珊溪水庫每一叢地震可以劃分成2個(gè)階段，開始階段地震間的時(shí)間間隔短、頻度高、震中位置集中，后一階段地震之間的時(shí)間間隔逐漸增長、頻度逐漸降低、震中開始向周邊遷移。因此，每一叢地震的開始階段由于地震密集發(fā)生，巖體破裂后水的滲透速率未能使巖石達(dá)到水飽和狀態(tài)，巖體主要表現(xiàn)為孔隙度增加、飽和度減小，從而導(dǎo)致波速比和P波速度的下降。后一階段由于地震間的時(shí)間間隔增加，水在巖體中的滲透更加充分，巖石的水飽和度逐漸增加，最終處于飽和狀態(tài)，波速比和P波速度也緩慢回升。隨著巖石的水飽和度增加，孔隙壓力增大，斷層面的有效剪應(yīng)力減小，斷層滑動(dòng)的危險(xiǎn)性增加，新的一叢地震又將開始。因此，每一叢地震的開始階段，波速比和P波速度較大，隨后逐漸減小。

3.4流體擴(kuò)散率和巖石孔隙度

假設(shè)水庫誘發(fā)地震的物理機(jī)制是流體作用，那么上述波速比和P波速度“下降-回升”變化的實(shí)質(zhì)就是“孔隙度增大(飽和度減小)-飽和度增大”變化，即波速比由極小值逐漸增大為極大值，就是巖石從不飽和狀態(tài)變化到飽和狀態(tài)的過程。Talwani 等[23]認(rèn)為水庫誘發(fā)地震是由于流體孔隙壓力前鋒傳遞到震源位置所致，并且定義了流體擴(kuò)散率αs=L2/T，其中L為孔隙壓力前鋒與震中的特征距離，T為延遲時(shí)間。根據(jù)這一假設(shè)，可以根據(jù)每一叢地震的波速比極小值和極大值，估算珊溪水庫的水力擴(kuò)散率。

“九五”數(shù)字化地震臺(tái)網(wǎng)建設(shè)項(xiàng)目完成以后，我國地震監(jiān)測能力有了很大的提高。珊溪水庫ML≥2.0地震能夠被浙江南部和福建北部的地震臺(tái)站記錄到，并在其中4個(gè)臺(tái)站中有清晰地震記錄，而2003年4月—2007年7月水庫區(qū)先后新建了8個(gè)測震臺(tái)，大大提高地震監(jiān)測能力，從而可以對(duì)珊溪水庫ML≥2.0地震進(jìn)行重新定位。鐘羽云等[15]使用速度結(jié)構(gòu)與震源參數(shù)聯(lián)合反演方法，進(jìn)行珊溪水庫地震重新定位，定位偏差在緯度方向上平均為0.37 km，經(jīng)度方向上平均為0.34 km，垂直方向上平均為0.39 km。本文使用鐘羽云等[15]的定位結(jié)果，估算珊溪水庫巖體水力擴(kuò)散率。

如上所述，每一叢地震的開始階段波速比和P波速度逐漸減小，后一階段則緩慢增大。表2給出了每一叢地震的后一階段。例如，2002—2003年發(fā)生的一叢地震，波速比由2002年8月30日的極小值1.66增大到2003年8月21日的極大值1.74，巖石從不飽和狀態(tài)變?yōu)轱柡蜖顟B(tài)，歷時(shí)T=356天。2002年8月30日ML2.6地震震中位于27.7037° N、119.9793° E，震源深度5 km， 2003年8月21日ML1.8地震震中位于27.6667° N、119.9667° E，震源深度9 km，兩次地震的距離L=5.7 km，計(jì)算得到珊溪水庫巖體水力擴(kuò)散率αs=1.06×104cm2s-1。考慮到定位誤差，地震位置不是一個(gè)確定性的點(diǎn)，而是一個(gè)橢球體內(nèi)的任何可能的點(diǎn)。計(jì)算時(shí)為了簡單起見，認(rèn)為地震位置是以震源坐標(biāo)為球心、定位誤差為半徑的球體內(nèi)的任何一點(diǎn)。本文選取定位誤差為0.39 km[15]，計(jì)算得到的珊溪水庫巖體流體擴(kuò)散率αs見表2。表2中流體擴(kuò)散率αs與Talwani 等[23]得到的美國南卡羅萊納水庫巖體水力擴(kuò)散率αs=5×103～5×105cm2s-1、Nascimento等[23]得到的巴西Acu水庫水力擴(kuò)散率αs=3.4×103～1.0×104cm2s-1、以及龔鋼延等[25]得到的廣東新豐江水庫水力擴(kuò)散率αs=6.2×104cm2s-1基本一致。

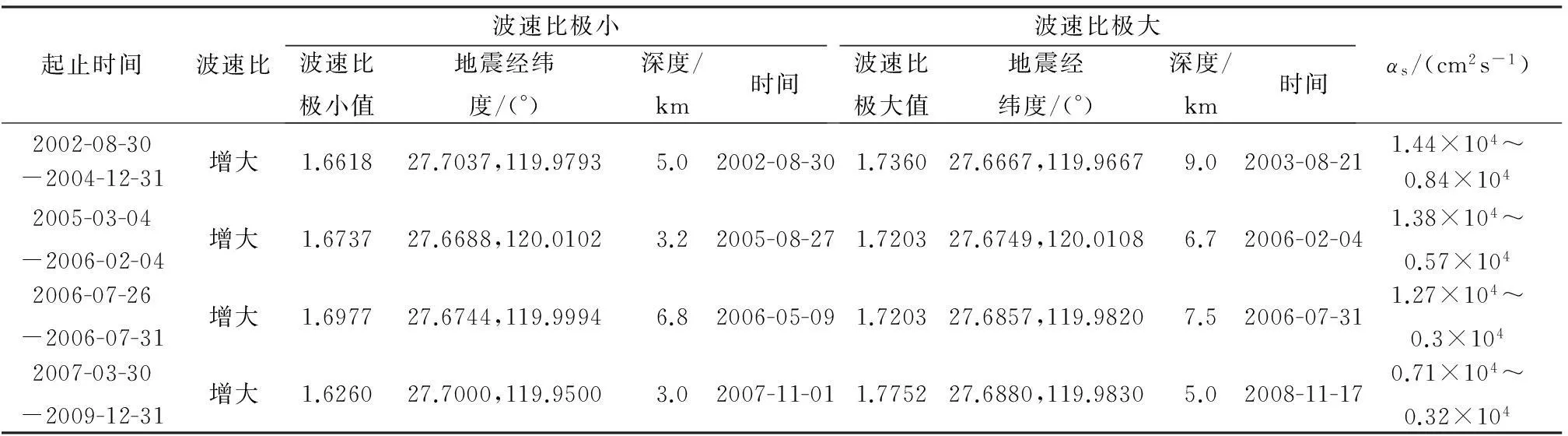
表 2　珊溪水庫巖體流體擴(kuò)散率估算值

假設(shè)地震時(shí)巖石處于水飽和狀態(tài)，即飽和度為100%，那么根據(jù)式(1)、(2)、(3)可以得到巖石孔隙度。珊溪水庫90%的地震波速比分布在1.66～1.75，根據(jù)式(1)～(3)得到珊溪水庫震中區(qū)巖石孔隙度分布在8.7%～2.0%。事實(shí)上，波速比與飽和度和孔隙度都有關(guān)，如果飽和度小于100%，那么波速比相同情況下計(jì)算得到的孔隙度會(huì)更小一些。因此8.7%～2.0%是珊溪水庫巖石孔隙度的上限值分布范圍。華東勘測設(shè)計(jì)研究院在工程地震勘察中，通過室內(nèi)巖石物理力學(xué)性質(zhì)試驗(yàn)測定了珊溪水庫壩址區(qū)侏羅系上統(tǒng)磨石山群d段新鮮流紋斑巖的孔隙度平均值為3.41%，與本文計(jì)算得到的數(shù)值一致。

4結(jié)論

水庫誘發(fā)地震的物理機(jī)制研究表明，水在水庫地震中起著重要作用，主要表現(xiàn)在兩個(gè)方面：一是水庫蓄水后水體載荷作用；二是流體滲流作用。假設(shè)珊溪水庫誘發(fā)地震的物理機(jī)制是流體作用，引入基于Gassmann方程的流體替換方法，根據(jù)珊溪水庫地震波速比和P波速度的變化特征， 分析討論珊溪水庫震中區(qū)巖石孔隙度和飽和度的變化，估算珊溪水庫水力擴(kuò)散率以及地震過程中巖石孔隙度的變化范圍，得到如下結(jié)論：

(1) 飽和度對(duì)波速比和P波速度的影響與巖石的飽水狀態(tài)有關(guān)。當(dāng)巖石接近飽和狀態(tài)時(shí)，波速比和P波速度均隨飽和度的增大而增大，兩者呈現(xiàn)出相同的變化趨勢(shì);當(dāng)巖石的飽和度較小時(shí)，波速比隨飽和度的增大而增大，P波速度則隨飽和度的增大而減小，兩者呈現(xiàn)出不同的變化趨勢(shì)。珊溪水庫地震波速比和P波速度的變化趨勢(shì)相同，說明珊溪水庫震中區(qū)巖石始終處于接近水飽和的飽水狀態(tài)。

(2) 假設(shè)珊溪水庫誘發(fā)地震的物理機(jī)制是流體作用，那么波速比和P波速度“下降-回升”的變化實(shí)質(zhì)上反映了震中區(qū)巖石“孔隙度增大(飽和度減小)-飽和度增大”的變化，每一叢地震的波速比由極小值逐漸增大為極大值是由于巖石從不飽和狀態(tài)變化到了飽和狀態(tài)。根據(jù)每一叢地震波速比的變化，可以得到珊溪水庫巖體的流體擴(kuò)散率αs=1.44×104～0.84×104cm2s-1，該數(shù)值與美國南卡羅萊納水庫、巴西Acu水庫、廣東新豐江水庫的流體擴(kuò)散率基本一致。

(3) 假設(shè)地震時(shí)巖石處于水飽和狀態(tài)，可以根據(jù)Gassmann方程計(jì)算得到珊溪水庫巖石孔隙度的上限值范圍為8.7%～2.0%，該數(shù)值與華東勘測設(shè)計(jì)研究院在工程地震勘察中通過室內(nèi)巖石物理力學(xué)性質(zhì)試驗(yàn)測定的孔隙度平均值結(jié)果一致。

參考文獻(xiàn)(References)

[1]劉遠(yuǎn)征，馬瑾，姜彤,等.庫水滲流與荷載對(duì)水庫地震形成的影響分析[J].地震地質(zhì)，2010,32(4):570-585.

LIU Yuan-zheng,MA Jin,JIANG Tong,et al.Analysis of Effect of Reservoir Water Seepage and Loading on the ccurrence of Earthquakes[J].Seismology and Geology,2010,32(4):570-585.(in Chinese)

[2]焦姣，郭安寧，高思如,等.水庫區(qū)地震前兆在地震預(yù)報(bào)中的意義[J].西北地震學(xué)報(bào)，2012，34(3):294-298

JIAO Jiao，GUO An-ning，GAO Si-ru,et al.Significance of the Earthquake Precursor in Reservoir Area for Earthquake Prediction[J].Northwestern Seismological Journal，2012，34(3):294-298.(in Chinese)

[3]馮德益,虞雪君，盛國英.波速異常的進(jìn)一步研究和問題討論(三)——水庫誘發(fā)地震前的vP/vS異常[J].西北地震學(xué)報(bào)，1993,15(3):38-43.

FENG De-yi,YU Xue-jun,SHENG Guo-ying.Further Study and Discussion on the Anomalies of Seismic Wave Velocity(Ⅲ)——vP/vSVariations before Reservoir Induced Seismic Events[J].Northwestern Seismological Journal,1993,15(3):38-43.(in Chinese)

[4]周連慶，趙翠萍，陳章立.紫坪鋪水庫地區(qū)尾波Qc值研究[J].地震,2009,29(4):44-51.

ZHOU Lian-qing，ZHAO Cui-ping，CHEN Zhang-li.Coda WaveQcValues in the Zipingpu Reservoir Area,Sichuan Province[J].Earthquake,2009,29(4):44-51.(in Chinese)

[5]王惠琳,張曉東，周龍泉,等.紫坪鋪水庫區(qū)域地殼Qs動(dòng)態(tài)變化及其與水庫蓄水關(guān)系的研究[J].地震學(xué)報(bào)，2012,34(5):676-688.

WANG Hui-lin， ZHANG Xiao-dong，ZHOU Long-quan，et al.Relationship between the Reservoir Storage and CrustalQs Dynamic Variation in Zipingpu Reservoir Area[J].Acta Seismologica Sinica，2012,34(5)：676-688.(in Chinese)

[6]盧顯,張曉東,周龍泉,等.紫坪鋪水庫區(qū)域地震波速比計(jì)算及研究[J].中國地震,2013,29(2):236-245.

LU Xian,ZHANG Xiao-dong,ZHOU Long-quan,et al.Calculation and Research onvP/vSRatio in the Zipingpu Reservoir Area[J].Earthquake Research in China, 2013,29(2):236-245.(in Chinese)

[7]張小濤，韓麗萍，張新東,等.河北邯鄲—邢臺(tái)地區(qū)波速比和泊松比分布特征研究[J].西北地震學(xué)報(bào)，2012，34(1):84-87.

ZHANG Xiao-tao,HAN Li-ping，ZHANG Xin-dong,et al.Distribution Characteristics of Wave Velocity Ratio and Poisson’s Ratio in Handan-Xingtai Areas，Hebei Province[J].Northwestern Seismological Journal,2012，34(1):84-87.(in Chinese)

[8]施行覺，徐果明，靳平,等.巖石的含水飽和度對(duì)縱、橫波速及衰減影響的實(shí)驗(yàn)研究[J].地球物理學(xué)報(bào)，1995，38：281-28.

SHI Xing-jue,XU Guo-ming,JIN Ping，et al.The Laboratory Study of Influence of Watersaturation on Rocks Velocity and Attenuation[J].Acta Geophysica Sinica，1995，38：281-28.(in Chinese)

[9]史謌，沈聯(lián)蒂.巖石含水飽和度、頻率、流體類型對(duì)聲波振幅影響規(guī)律的探討[J].北京大學(xué)學(xué)報(bào):自然科學(xué)版，1993，29(4):458-465.

SHI Ge,SHEN Lian-di.The Investigation of the Influence of the Degree of Saturation,Frequency and Fluid Type on the Sonic Wave Amplitude in Sandstones,Aeta Scientiarum Naturalium Universitatis Pekinensis[J].,993，29(4):458-465.(in Chinese)

[10]馬淑芳，韓大匡，甘利燈，等.地震巖石物理模型綜述[J].地球物理學(xué)進(jìn)展，2010，25(2)：460-471.

MA Shu-fang,HAN Da-kuang,GAN Li-deng,et al.A Review of Seismic Rock Physics Models[J].Progress in Geophys,2010,25(2):460-471.(in Chinese)

[11]Gassmann F.Elastic Waves through a Packing of Spheres[J].GeoPhysics，1951，(16)：673-682.

[12]云美厚,丁偉,楊長春.油藏水驅(qū)開采時(shí)移地震監(jiān)測巖石物理基礎(chǔ)測量[J].地球物理學(xué)報(bào)，2006，49(6)：1813-1818

YUN Mei-hou，DING Wei，YANG Chang-chun.Petrephysical Measurements for Time-lapse Seismic Monitoring of Reservoir Waterllooding Recovery[J].Chinese Journal of Geophysics，2006，49(6)：1813-1818.(in Chinese)

[13]云美厚 ，管志寧.儲(chǔ)層條件下砂巖縱波和橫波速度的理論計(jì)算[J].石油物探， 2002,41(3):289-298.

YUN Mei-hou，GUANG Zhi-ning,The Estim Ation of P and S-wave Velocities in Sandstone under In-situ Conditions[J].Geophysical Prospecting for Petroleum,2002,41(3):289-298.(in Chinese)

[14]馬中高.Biot系數(shù)和巖石彈性模量的實(shí)驗(yàn)研究[J].石油與天然氣地質(zhì)，2008,29(1):135-140.

MA Zhong-gao.Experimental Investigation into Biot’s Coefficient and Rock Elastic Moduli[J].Oil&Gas Geology,2008,29(1):135-140.(in Chinese)

[15]鐘羽云，張帆，趙冬.珊溪水庫ML4.6震群精確定位與發(fā)震構(gòu)造研究[J].地震研究,2011,34(2):158-165.

ZHONG Yu-yun，ZHANG Fan，ZHAO Dong.Precise Relocation and Seismogenic Structure of the Shanxi Reservoir Earthquake Sequence in Wenzhou，Zhejiang Provinc[J].Journal of Seism Ological Research,2011,34(2):158-165.(in Chinese)

[16]劉素梅,徐禮華，李彥強(qiáng).丹江口水庫巖石物理力學(xué)性能試研究[J].華中科技大學(xué)學(xué)：城市科學(xué)版.2007，24(4)：54-58.

LIU Su-mei,XU Li-hua,LI Yan-qian.Exper imental Study on Rock Physical and Mechanical Properties in Danjiangkou Reservoir Area[J].J of HU ST:Urban Science Edition,2007,24(4):54-58.(in Chinese)

[17]蔣海昆,張曉東，單新建，等.中國大陸水庫地震統(tǒng)計(jì)特征及預(yù)測方法研究[M].北京：地震出版社，2014：115-119.

JIANG Hai-kun,ZHANG Xiao-dong,SHAN Xin-jian,et al.Research on Statistical Characteristics and Prediction Methods of Reservoir Earthquake in Chinese Mainland[M].Beijing:Seismological Press,2014:115-119.(in Chinese)

[18]鐘羽云,張震峰,闞寶祥.溫州珊溪水庫地震重新定位與速度結(jié)構(gòu)聯(lián)合反演[J].中國地震,2010,26(3):265-272.

ZHONG Yu-yun，ZHANG Zhen-feng，KAN Bao-xiang.Simultaneous Inversion of Earthquake Relocation and Velocity Structure in the Shanxi-reservoir,Wenzhou[J].Earthquake Research in China,2010,26(3):265-272.(in Chinese)

[19]馮德益.地震波速異常[M].北京：地震出版社，1981:1-14.

FENG De-yi.Seismic Velocity Anomalies[M].Beijing:Seismological Press,1981:1-14.(in Chinese)

[20]鐘羽云，周昕，張帆,等.2006年溫州珊溪水庫地震序列特征[J].華南地震，2007,27(1):21-30.

ZHONG Yu-yun，ZHOU Xin，ZHANG Fan,et al.Seismic Sequence Characteristics of the 2006 Shanxi Reservoir Earthquake in Wenzhou[J].South China Journal of Selsmology,2007,27(1):21-30.(in Chinese)

[21]周龍泉，劉桂萍，馬宏生，等.利用重復(fù)地奪觀測地殼介質(zhì)變化[J].地震，2007，27(3)：1-9.

ZHOU Long-quan,LIU Gui-ping,MA Hong-sheng,et al.Monitoring Crustal Media Variation by Using Repeating Earthquakes[J].Earthquake,2007,27(3):1-9.(in Chinese)

[22]熊紹柏，劉宏兵，王有學(xué)，等.華南上地殼速度分布與基度、蓋層構(gòu)造研究[J].地球物理學(xué)報(bào)，2002，45(6)：784-791.

XIONG Shao-bai,LIU Hong-bing,WANG You-xue,et al.A Study on Velocity Distributton in Uppercrustand Tectonics of Basem ent and Cover in South China[J].Chinese Journal of Geophysics,2002,45(6):784-791.(in Chinese)

[23]Talwani P，Acre S.Pore Pressure Difusion and the Mechanism of Reservoir Induced Seismicity[J].PAGEOPH，1985,122(1984/85):947-965.(in Chinese)

[24]Nascimento A F, Lunn R J,Cowie P A.M ondeling the Heterogeneous Hydraulic Properties of Faults Using Constraints from Reservoir-induced Seismicity[J].J Geophys Res,2004,110(B09201):1-17.

[25]龔鋼延,謝原定.新豐江水庫地震區(qū)內(nèi)孔隙流體擴(kuò)散與原地水力擴(kuò)散率的研究[J].地震學(xué)報(bào)，1991, 13(3):364-371.

GONG Gang-yan XIE Yuan-ding,Research on the Diffusion of Pore Fluid and In-situ Hydraulic Diffusivity in the Epicentral Region of Xinfengjiang Reservoir Earthquakes[J].Acta Seismologica Sinica,1991,13(3):364-371.(in Chinese)

[26]馮銳.新豐江6.1級(jí)水庫地震前后的波速比變化[J].地球物理學(xué)報(bào),1977,20(3):211-221.

FENG Rui.On the Variations of the Velocity Ratio Before and After the Xinfengjiang Reservoir Impounding Earthquake ofM6.1[J].Acta Geophysica Sinica,1977,20(3):211-221.(in Chinese)

[27]林凱，賀振華，熊曉軍,等.基于Gassmann方程的流體替換流程[J].長江大學(xué)學(xué)報(bào)：自然科學(xué)版，2009， 6(1)：180-181.

LIN Kai,HE Zhen-hua,XIONG Xiao-jun,et al.Fluid Replacement Process Based on Gassmann Equation[J].Journal of Yangtze University:Nat Sci Edit,2009，6(1)：180-181.(in Chinese)