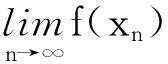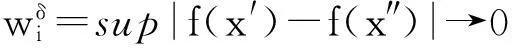有界函數(shù)可積條件的推廣

張　輝，余桂東

(安慶師范學院 數(shù)學與計算科學學院, 安徽 安慶 246133)

?

有界函數(shù)可積條件的推廣

張輝，余桂東

(安慶師范學院 數(shù)學與計算科學學院, 安徽 安慶 246133)

摘要：對數(shù)學分析教材中關于有界函數(shù)可積性的條件進行了推廣，并且從測度的角度進一步解釋了可以推廣的原因。

關鍵詞：有界函數(shù)；可積條件；測度

在《數(shù)學分析》[1]教材中關于函數(shù)的可積性有如下兩個結論：

定理1[1]若f在[a,b]上連續(xù)，則f在[a,b]上可積。

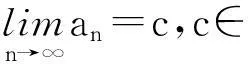
從教學的角度考慮，定理1與定理2都有推廣的必要，因為可以提出下面兩個問題：(1)定理1的閉區(qū)間[a,b]上連續(xù)能否改成開區(qū)間(a,b)上連續(xù)， (2)定理2中結論能否推廣到有限極限的情形。對于問題(1)一般的回答是否定的，例如

對于問題(2)，從《實變函數(shù)論》[2]中的測度論角度知道回答是肯定的。本文主要目的是利用定積分的定義證明下面兩個定理：

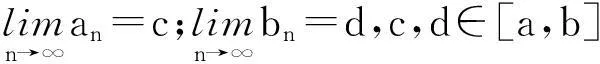
由定理3，很容易得到如下的推論。

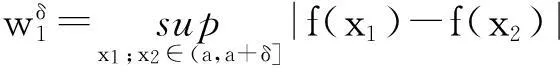
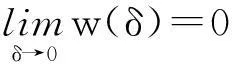
利用歸結原理以及函數(shù)極限的Cauchy收斂準則，得到了下面一個有趣的結論：

1.1.1 秸稈機械還田 秸稈直接還田是當前揚州市乃至江蘇省秸稈綜合利用最主要的途徑。2016年，揚州市實現(xiàn)稻麥秸稈還田206.59萬t，還田面積30.1萬hm2，還田率達66.57%。秸稈還田區(qū)域主要集中在寶應、江都、高郵3縣(市、區(qū))，還田量分別達總量的39.96%、21.2%和20.49%。

1定理的證明

引理1[1]若f為[a,b]上的有界函數(shù)，則f在[a,b]上可積的充要條件是對于任意的ε>0，存在[a,b]上的某個分割T，使得

wi=Mi-mi表示f在Δi上的振幅。

引理2[1]若f是[a,b]上只有有限個間斷點的有界函數(shù)，則f在[a,b]上可積。

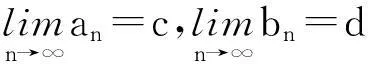
則在閉區(qū)間H=[a,b]-{(c-ε,c+ε)∪(d-ε,d+ε)}上至多只有有限個間斷點。結合引理(1)，(2)可知，存在H上某個分割T使得

結合引理1得證。

注1《實變函數(shù)論》中函數(shù)Riemann黎曼可積的充要條件是幾乎處處連續(xù)，即不連續(xù)點的測度為零。 因此定理3的條件可以進一步放寬到可數(shù)個間斷點，一個重要的例子是黎曼函數(shù)

R(x)在[0,1]中的間斷點為Q∩[0,1]，它是可數(shù)集，因而在[0,1]上黎曼可積，但是卻不能用定理3來判斷。

m

(1)若ε<δ，則分割T結合閉區(qū)間[a,a+ε][a+ε,a+δ]以及[b-ε,b][b-δ,b-ε]構成[a,b]的一個分割T′，則

其中K=2[(M-m)+(b-a)]+1。

(2)若ε≥δ, 則分割T結合閉區(qū)間[a,a+δ]以及[b-δ,b]構成[a,b]的一個分割T′，則

其中L=2(M-m)+1。綜上，由有界可積函數(shù)的充要條件知f(x)在[a,b]上可積。

|f(xn1)-f(xn2)|<ε

參考文獻:

[1] 葉淼林等.數(shù)學分析(上) [M]. 合肥：中國科學技術大學出版社，2012.

[2] 周民強.實變函數(shù)論[M]. 北京： 北京大學出版社，2001.

Extension about Bounded Integrable Function

ZHANG Hui，YU Gui-dong

(School of Mathematics and Computation Science，Anqing Teachers College，Anqing 246133，China)

Abstract:This paper extends the integrability conditions about bounded function in mathematical analysis textbook, and further explains the reason from the perspective of measure theory.

Key words:bounded function, integrability conditions, perspective of measure theory

中圖分類號：O231.9

文獻標識碼：A

文章編號：1007-4260(2015)01-0099-02

DOI：10.13757/j.cnki.cn34-1150/n.2015.01.027

作者簡介：張輝，男，安徽桐城人，博士，安慶師范學院數(shù)學與計算科學學院講師， 研究方向為偏微分方程及其應用。

收稿日期：2014-04-15