關(guān)于施密特正交化的一點(diǎn)注釋與應(yīng)用

蔡 改 香

(安慶師范學(xué)院 數(shù)學(xué)與計(jì)算科學(xué)學(xué)院，安徽 安慶 246133)

?

關(guān)于施密特正交化的一點(diǎn)注釋與應(yīng)用

蔡 改 香

(安慶師范學(xué)院 數(shù)學(xué)與計(jì)算科學(xué)學(xué)院，安徽 安慶 246133)

摘要：高等代數(shù)中求標(biāo)準(zhǔn)正交基、求正交陣都要用到施密特正交化。歐式空間的基中向量的位置不同，經(jīng)過施密特正交化所得到的標(biāo)準(zhǔn)正交基的結(jié)果也不同，并且計(jì)算量的大小也不同。用施密特正交化法求實(shí)對稱矩陣的逆矩陣是一種新的方法。

關(guān)鍵詞：基，標(biāo)準(zhǔn)正交基，施密特正交化

高等代數(shù)中，歐式空間的一組線性無關(guān)的向量張成一個子空間[1]，那么這一組向量就稱為這個子空間的一個基。施密特正交化提供了一種方法，能夠通過這一子空間上的一個基得出子空間的一個正交基，并可進(jìn)一步求出對應(yīng)的標(biāo)準(zhǔn)正交基。從幾何上說，正交基就像一個歐式空間的直角坐標(biāo)系，比如三維空間的x軸，y軸，z軸，沒有正交化的就是非歐幾何，如用(1,0,0)，(1,1,0)，(1,1,1)也可以作為一組基，但別的向量用這組基表示不方便。其實(shí)用正交基的好處在于數(shù)值計(jì)算上，不用正交基的話計(jì)算不穩(wěn)定，會隨著計(jì)算過程逐步積累誤差，可能會使得誤差過大而使計(jì)算結(jié)果根本不可用，而正交基則不會發(fā)生這種問題。

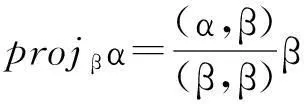
是正交于子空間Vm[4]，即β正交于Vm的正交基α1,α2,…,αm，因此只要將β單位化，即

那么α1,α2,…,αm,αm+1就是Vm在α上擴(kuò)展的子空間span{α,α1,α2,…,αm}的標(biāo)準(zhǔn)正交基。根據(jù)上面的分析，對于向量組α1,α2,…,αm張成的空間span{α1,α2,…,αm}，只要從其中的一個向量，不妨設(shè)為α1，所張成的一維子空間span{α1}開始(注意到{α1}就是span{α1}的正交基)，重復(fù)上述擴(kuò)展構(gòu)造正交基的過程，就能夠得到Vm的一組正交基。這就是施密特正交化的思想。首先需要確定擴(kuò)展正交基的順序，不妨設(shè)為α1,α2,…,αm，施密特正交化的過程如下[1]，

第一步：正交化

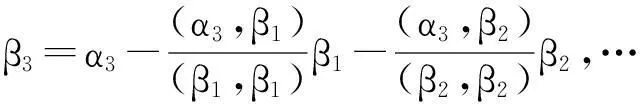
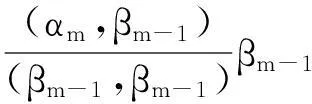
第二步：單位化

這樣就得到span{α1,α2,…,αm}上的一組正交基β1,β2,…,βm以及標(biāo)準(zhǔn)正交基η1,η2,…,ηm。

定理1設(shè)α1,α2,…,αn是歐氏空間V(n)的一組基，則一定存在V的一組標(biāo)準(zhǔn)正交基η1,η2,…,ηn，使由基α1,α2,…,αn到η1,η2,…,ηn的過渡矩陣為上三角形且主對角線上元素均大于0。

證明由施密特正交化的過程，由基α1,α2,…,αn到標(biāo)準(zhǔn)正交基η1,η2,…,ηn的過渡矩陣是上三角陣

顯然T的主對角線上元素均大于0。

對一組線性無關(guān)的向量施行施密特正交化時，從理論上來說，β1的選取是隨意的，由定理1，β1的選取不同導(dǎo)致施密特正交化所得的標(biāo)準(zhǔn)正交基也是不同的。并且選取β1不同使得計(jì)算過程中的計(jì)算量也是不同的，下面舉例說明。

例1用施密特正交化方法，將R3中基α1=(1,1,1),α2=(0,1,1),α3=(0,0,1)化為標(biāo)準(zhǔn)正交基。

第二步單位化：

得η1,η2,η3為標(biāo)準(zhǔn)正交基。顯然這兩組標(biāo)準(zhǔn)正交基是不一樣的，且前面這種β1的選取方法為我們的計(jì)算帶來了方便。

歐式空間的標(biāo)準(zhǔn)正交基一定存在，但不一定唯一，由同一組基出發(fā)變成標(biāo)準(zhǔn)正交基的結(jié)果也可以不唯一，它和向量的排序有關(guān)系。顯然向量按前面這種排序，計(jì)算量要小些。從上解法我們發(fā)現(xiàn)將簡單的向量如分量中零元素比較多的向量視為施密特正交化的第一個向量β1，依此類推。這樣可以簡化計(jì)算。

逆矩陣的求法有待定系數(shù)法、伴隨矩陣法、初等變換法[5]等，下面就實(shí)對稱矩陣給出其逆矩陣的一種新的求法：施密特正交化法。

定理2[1]任意一個n階實(shí)對稱矩陣A，都存在一個n階正交矩陣P，使得

其中λ1,λ2,…,λn為A的特征值。由定理2，實(shí)對稱矩陣A的逆矩陣A-1=PΛ-1P-1=PΛ-1PT，由于正交矩陣的逆矩陣很容易求，為其轉(zhuǎn)置矩陣，這樣求A的逆矩陣關(guān)鍵是求正交矩陣。

解|λE-A|=(λ+7)(λ-2)2，A的特征值為λ1=-7,λ2=λ3=2。相應(yīng)的特征向量為

α1=(1,2,-2),α2=(-2,1,0),α3=(2,0,1)

正交化，得β1=(1,2,-2),β2=(-2,1,0),

參考文獻(xiàn):

[1]北京大學(xué)數(shù)學(xué)系幾何與代數(shù)教研室前代數(shù)小組.高等代數(shù)[M].北京:高等教育出版社, 2003.

[2]胡萬寶.高等代數(shù)[M].合肥:中國科學(xué)技術(shù)大學(xué)出版社,2013.

[3]呂林根.解析幾何(第四版)[M]. 北京:高等教育出版社, 2010.

[4]李麗. 線性代數(shù)教學(xué)中兩個問題的幾何解釋[J].赤峰學(xué)院學(xué)報(bào)(自然科學(xué)版)，2013(21):3-4.

[5]高明.逆矩陣的求法[J].陰山學(xué)刊(自然科學(xué)版),2006(2):14-16.

A Note and Application of the Schmidt Orthogonalization

CAI Gai-xiang

(School of Mathematics & Computational Science, Anqing Teacher College，Anqing 246133, China)

Abstract:In higher algebra, we have used the Schmidt orthogonalization to solve standard orthogonal basis and the orthogonal array. This paper mainly introduces if positions of vectors are different in the base of Euclidean space, then the standard orthogonal basis obtained through the Schmidt orthogonalization is different, and the amount of calculation is different. This paper also introduces the method of solving the inverse matrix of real symmetric matrix by using Schmidt orthogonalization.

Key words:basis, standard orthogonal basis, Schmidt orthogonalization

中圖分類號：O151.21

文獻(xiàn)標(biāo)識碼：A

文章編號：1007-4260(2015)01-0106-03

DOI：10.13757/j.cnki.cn34-1150/n.2015.01.030

作者簡介：蔡改香，女，安徽廬江人，碩士，安慶師范學(xué)院數(shù)學(xué)與計(jì)算科學(xué)學(xué)院講師， 研究方向?yàn)樽V圖理論及其應(yīng)用。

基金項(xiàng)目：安慶師范學(xué)院青年科研基金項(xiàng)目(KJ201307)。

收稿日期：2014-06-28