基于最小二乘法的單擺實驗數據處理

王　鵬，刁山菊，張季謙

(1. 江蘇省句容市第三中學，江蘇 句容 212400 ;2. 安徽師范大學 物理與電子信息學院，安徽 蕪湖 241000)

?

基于最小二乘法的單擺實驗數據處理

王鵬1，刁山菊1，張季謙2

(1. 江蘇省句容市第三中學，江蘇 句容 212400 ;2. 安徽師范大學 物理與電子信息學院，安徽 蕪湖 241000)

摘要：結合單擺實驗實測數據，運用origin作圖軟件建立數學模型和相關系數檢驗，采用最小二乘法計算南京地區的重力加速度，并與平均值法與逐差法進行數據處理比較。實驗計算結果表明，利用最小二乘法計算重力加速度準確可靠，誤差僅為0.028%。上述方法也可很好地應用于基礎物理實驗中其它線性關系變量試驗數據的分析與處理過程。

關鍵詞：最小二乘法；單擺實驗；重力加速度；線性擬合

重力加速度的測量是基礎物理實驗中一個重要的力學實驗[1, 2]。近年來，一些物理實驗教學工作者已經對此實驗進行了深入的研究，包括實驗裝置的改進與智能化[3-8]、實驗方法的優化與創新[9-13]、數據的信息化處理[14, 15]與誤差分析[16,17]等。然而，目前關于利用最小二乘法原理處理單擺實驗數據，計算重力加速度的研究未見報道。基于單擺實驗實測數據，運用Origin作圖軟件建立數學模型和相關系數檢驗[18]，采用最小二乘法的線性擬合計算南京地區的重力加速度，并與平均值法與逐差法進行數據處理比較。

1實驗原理

1.1　單擺模型

一根不可伸長且質量不計的細線下端懸掛一個小球，上端固定。當小球的直徑遠小于細線的長度時，可把小球看作是一個質點。如果把懸掛的小球自平衡位置拉至一邊保持擺角θ<5°，小球可在平衡位置附近作周期性擺動，即簡諧振動。這種裝置稱為單擺，如圖1所示。

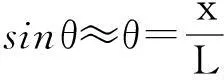
1.2　最小二乘法原理

已知兩變量為線性關系y=kx+b，實驗獲得其n組含有誤差的數據(xi,yi)。若將這n組數據代入方程求解，則k， b 之值無確定解。最小二乘法提供了一個求解的方法，其基本思想是擬合出一條“最接近”這n個點的直線。在這條擬合的直線上，各點相應的y 值與測量值對應縱坐標值之偏差的平方和最小。根據統計理論，參數k和b計算公式[19]

(1)

(2)

1.3　相關系數γ

相關系數γ表示數據(xi,yi)相互聯系的密切程度，以及擬合所得的線性方程的可靠程度。γ的計算公式如下[19]

(3)

其中，γ的值在- 1~ + 1 之間。γ的絕對值越接近1, 表明(xi,yi)相互聯系越密切, 線性方程的可靠程度越高，線性越好。

2最小二乘法擬合單擺實測數據

當單擺的線長L從50cm以10cm為步長增加到120cm時，分別測量出每根擺線長對應的單擺擺動時間t。其中，基于計算簡便，本實驗的有效擺長直接采用擺線長L，沒有再加上小球的半徑D/2。同時，注意保證擺球速度方向和重力方向的共面，防止出現圓錐擺運動。為了減小計時誤差，單擺周期T測量采用平衡位置開始計時，且多周期測量取平均值。每次擺動測量取N=40個周期T，實驗數據如表1所示。

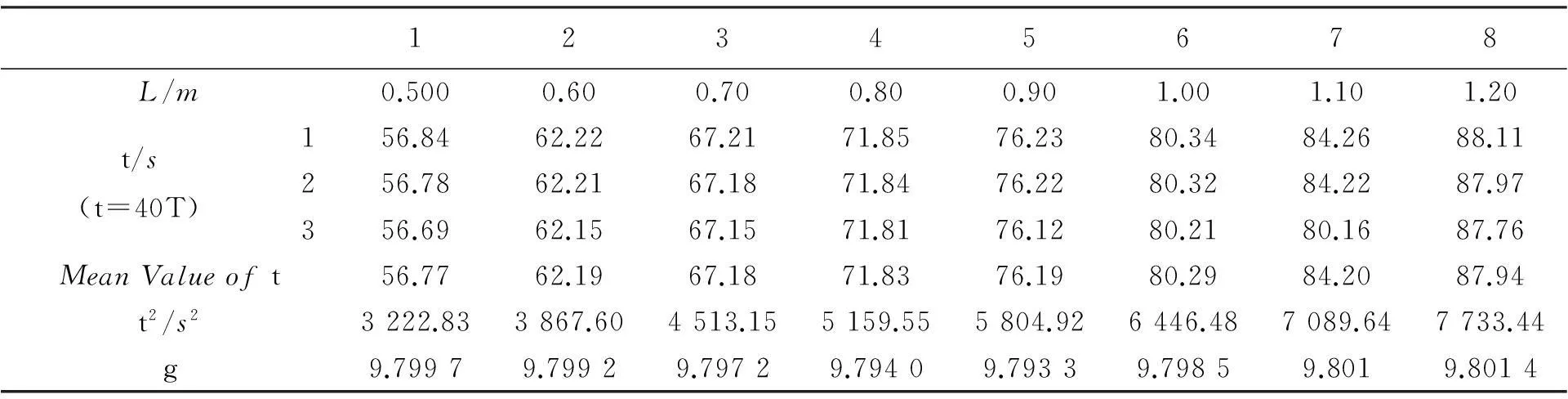
表1　擺角時單擺線長L與單擺擺動時間t

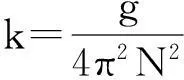
本實驗中有一點值得注意：L與t2的關系滿足正比例函數y=kx，因此如果實驗測量準確，(t2,L)圖像應該是一條通過坐標原點的直線。但最小二乘法線性擬合出的結果存在一個截距，且散點圖左移而不通過坐標原點，原因是我們采用的是單擺的擺線長L，而不是單擺的有效擺長L+D/2。這種處理對斜率計算結果不會造成影響，由斜率求得的重力加速度g仍準確可靠。

3最小二乘法與平均值法、逐差法的數據處理比較

3.1　基于平均值法的g值數據處理

3.2　基于逐差法的g值數據處理

若兩變量滿足線性關系y=kx，通過逐差法分析與處理M組實測數據(xi,yi)擬合出線性函數方程時，無誤差自變量x以等步長d值遞增，即xi+1-xi=d，擬合是在y方向進行，且M=2m是偶數。根據統計理論，直線斜率K值的擬合公式[20]

(4)

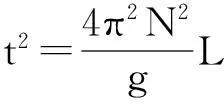
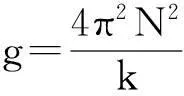
3.3　三種數據處理方法的結果比較

從表2中可以看出，最小二乘法處理實測數據，計算重力加速度g值更加接近理論值g=9.794 9m·s-2，相對誤差較小，具有較高的準確性，且符合嚴格的統計理論。逐差法產生的誤差較大，是因為實驗數據的取樣個數對處理結果會產生極大影響。

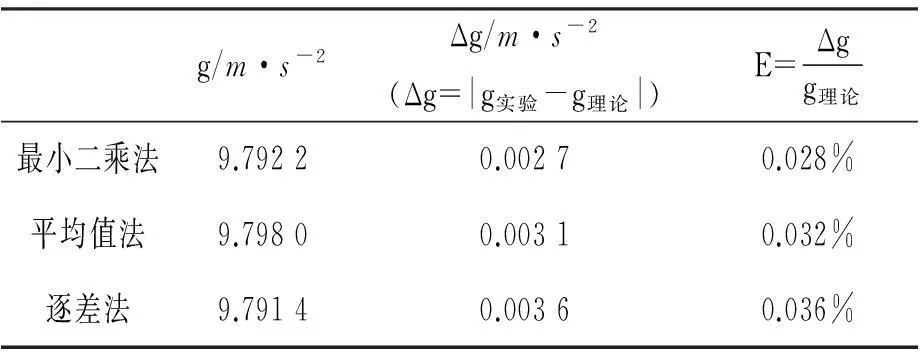
表2　三種數據處理方法的g，Δg及相對誤差E值

然而，從數據處理的過程來看，利用最小二乘法及逐差法進行數據處理，較為繁瑣與費時，手工計算量大。因此，可以結合計算機編程軟件，如FORTRAN 語言與C語言，將最小二乘法編寫出計算機程序，進而實現數據處理信息化，這也是我們下一步工作的方向。

4結束語

在基礎物理實驗的數據處理中，直線擬合是一個極其重要的數據處理手段。采用線性回歸分析與最小二乘法，對單擺實驗的數據進行線性擬合處理，并與教材使用的平均值法和逐差法處理實驗數據進行比較。通過圖像斜率，計算了南京當地的重力加速度，相對誤差約為0.028%。利用這種方法和原理，可以有效地提高數據處理的準確性，在線性關系變量的實際求解中有著極其重要的作用。

參考文獻:

[1] 春寧. 測定重力加速度的幾種方法[J]. 赤峰學院學報(自然科學版), 2007, 23(6): 5-7.

[2] 田勝安，張波. 探究單擺周期與重力加速度關系的實驗改進[J]. 物理教學探討, 2013, 31(6): 67-68.

[3] 韓定安，曾亞光，陳曉龍，梁永根. 基于 Labview平臺的重力加速度測量系統[J]. 實驗室研究與探索，2007, 26(11): 33-35.

[4] 袁樹青.自由落體法測重力加速度的智能系統[J]. 太原師范學院學報(自然科學版)，2009，8(4):81-84.

[5] 郭敏強，郭啟凱，王偉麗，聶士忠. 基于單片機的單擺法智能重力加速度測量裝置的研制[J]. 科學技術與工程, 2012, 12(26): 6766-6771.

[6] 趙武，王新春，祝菲霞，王昆林. 用氣軌系統Spss測定重力加速度[J]. 楚雄師范學院學報，2013, 28(9): 35-39.

[7] 劉建偉，王新春. 用改進的單擺實驗系統與Spss標定重力加速度[J]. 大學物理實驗, 2013, 26(4):56-59.

[8] 高鵬，李得東，孟祥省. 基于PASCO系統的重力加速度測定[J]. 物理實驗，2014, 34(3): 44-47.

[9] 李應發. 測量重力加速度的一種新方法[J]. 貴州師范大學學報(自然科學版)，2012,30(5): 76-79.

[10] 朱道云，龐瑋. 多管落球法測量重力加速度[J]. 實驗技術與管理，2012, 29(4): 59-61.

[11] 雷達，孟根其其格，李淑俠，周曉娟. 基于阿基米德定律測量重力加速度[J]. 大學物理實驗，2013,26(4): 37-39.

[12] 漢澤，西徐岳，甘志強. 利用多普勒效應測定重力加速度[J]. 計量與測試技術，2009,36(8):32-33.

[13]吉明榮，王新春. 用自制圓錐擺與Spss標定重力加速度[J]. 楚雄師范學院學報, 2013, 28(3): 18-23.

[14] 訾振發，于淼. Origin8.0軟件在單擺實驗中的應用[J]. 大學物理實驗，2013, 26(1): 75-77.

[15] 顧芳，張加宏. 用Excel研究單擺測重力加速度實驗中的隨機誤差分布規律[J]. 大學物理實驗，2010,23(4): 72-74.

[16] 王金德. “單擺測重力加速度”的實驗研究與誤差分析[J]. 銅仁學院學報, 2011, 13(3): 126-128.

[17] 古麗賈瑪力·哈那比亞. 利用單擺測量重力加速度及其不確定度的討論[J]. 吉林省教育學院學報, 2012, 28(8): 149-151.

[18]王鵬，刁山菊，張季謙. Origin在中學物理實驗教學中的應用研究[J]. 安慶師范學院學報(自然科學版)，2014，20(2):139-142.

[19] 蘭燕娜. 基于VB語言實現最小二乘法直線擬合[J]. 長江大學學報, 2011, 8(6): 92-94.

中圖分類號：O322

文獻標識碼：A

文章編號：1007-4260(2015)01-0136-04

DOI：10.13757/j.cnki.cn34-1150/n.2015.01.039

通訊作者：張季謙，男，安徽太湖人，博士，安徽師范大學物理與電子信息學院教授，主要從事理論生物物理、復雜體系非線性動力學、理論物理等方面的研究工作。

作者簡介：王鵬，男，安徽六安人，安徽師范大學物理與電子信息學院理學碩士，江蘇省句容市第三中學一級教師，主要從事中學物理教學與研究。