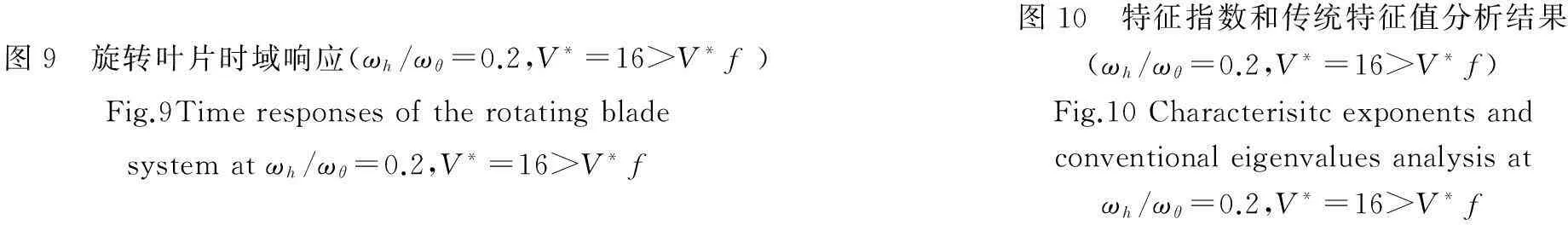基于Floquet理論的旋轉風機葉片動力失速氣彈穩定性研究

李迺璐 ， 穆安樂， Balas M J

(1.揚州大學 水利與能源動力工程學院，江蘇 揚州　225127； 2. 西安理工大學 機械與精密儀器工程學院，西安　710048；3. 美國安柏瑞德航空航天大學 航空學院，美國　32114)

?

基于Floquet理論的旋轉風機葉片動力失速氣彈穩定性研究

李迺璐1， 穆安樂2， Balas M J3

(1.揚州大學 水利與能源動力工程學院，江蘇 揚州225127； 2. 西安理工大學 機械與精密儀器工程學院，西安710048；3. 美國安柏瑞德航空航天大學 航空學院，美國32114)

大型風力發電機在大攻角處容易發生氣流分離狀態，并引發失速顫振。失速顫振會對大型風力機安全穩定的運行造成巨大的危害，不僅嚴重影響發電效率還會造成風機葉片的損壞。因此研究失速顫振問題非常重要。針對風機葉片失速氣彈穩定性的研究問題，需要采用氣動失速模型。目前實用性強的氣動失速模型為ONERA模型[1]和Beddoes-Leishman(B-L)模型[2]。任勇生等[3-4]多次采用ONERA非線性失速模型模擬大攻角處的氣動升力和升力矩，用于動力失速非線性氣彈穩定性研究，但是都是針對靜態氣動特性，即非時變氣彈系統。B-L 模型為半經驗動態失速非定常模型[5]，考慮了附著流，前緣分離和可壓縮性等動態翼型擾流物理特性，可以較好地模擬風機葉片非定常氣動力與動態失速特性。劉廷瑞[6]基于此模型采用擬合氣彈系數法分析了大型風力機葉片的氣彈穩定性，但是分析對象為葉片在每個靜態攻角處的系統氣彈特性，并非針對攻角時刻變化的旋轉葉片進行整體氣彈特性分析。對于靜態點的葉片氣動負載計算無論在公式建模上還是微分方程求解上都相對簡單一些，而針對旋轉葉片的周期時變氣動負載計算就較為困難和復雜，氣動負載不僅需要滿足旋轉葉片的固有周期時變特性，又要能夠描述葉片的動態失速特性及失速全過程。

關于風機葉片氣彈穩定性的研究大多都針對靜態葉片振動系統，即非時變線性氣彈系統，所以特征值法被廣泛應用于氣彈穩定性分析中。文獻[7]采用計算系統狀態矩陣特征值的方法來分析風機葉片經典顫振系統的氣彈穩定性；文獻[4]利用特征值分析結果觀察當風速改變時，葉片從穩定過度到發散的過程。文獻[8]采用特征值技術進行葉片顫振性能的數值求解。特征值法的局限性在于只能分析非時變系統的氣彈穩定性，針對旋轉葉片這類時變氣彈系統，傳統的特征法不再適用。

針對上述問題，本文根據旋轉葉片攻角周期變化的特征利用B-L模型計算出周期時變的動態失速氣動負載，基于時變氣彈系統模型，采用Flqouet理論進行系統的氣彈穩定性分析，并通過時域響應加以驗證。通過分析結果來揭示固有頻率比和結構阻尼對旋轉風機葉片失速顫振邊界的影響。

1旋轉葉片振動模型

1.1時變振動方程

考慮旋轉葉片的翼型為UA97W300-I0，隨著風機的旋轉，葉片上的非定常氣動力也跟著周期性變化，旋轉葉片振動運動系統為揮舞扭轉耦合的周期時變氣彈系統。振動運動位移由揮舞彎曲位移h和扭轉偏移角度θ表示(見圖1)。b為葉片截面的半弦長，重心與彈性軸的距離為xθb, 葉片的振動受制于彎曲力Qh和扭轉力Qθ。兩自由度揮舞-扭轉耦合的結構模型運行方程可表示為[9]：

(1)

式中：m為葉片截面的質量，Iθ為關于彈性軸的質量矩，Ch,Cθ為結構阻尼系數，Kh,Kθ為揮舞，扭轉彈簧常量。彎曲力Qh和扭轉力Qθ表示為：

(2)

式中：ρ為空氣密度，V為相對風度，Cl,θ,Cm,θ為氣動升力和氣動力矩系數,包含Cl,θ,Cm,θ的時變項表示旋轉葉片的周期時變氣動力變化，將由非線性氣動失速模型來模擬，彎曲力和扭轉力的常量項是由UA97W300-I0翼型為非對稱翼型而產生的氣動力。這是由于非對稱翼型葉片的靜態氣動力在攻角為零并非為零。根據UA97W300-I0翼型的靜態氣動升力和氣動力矩求得攻角為零時的氣動系數為0.246 3和-0.145 6。

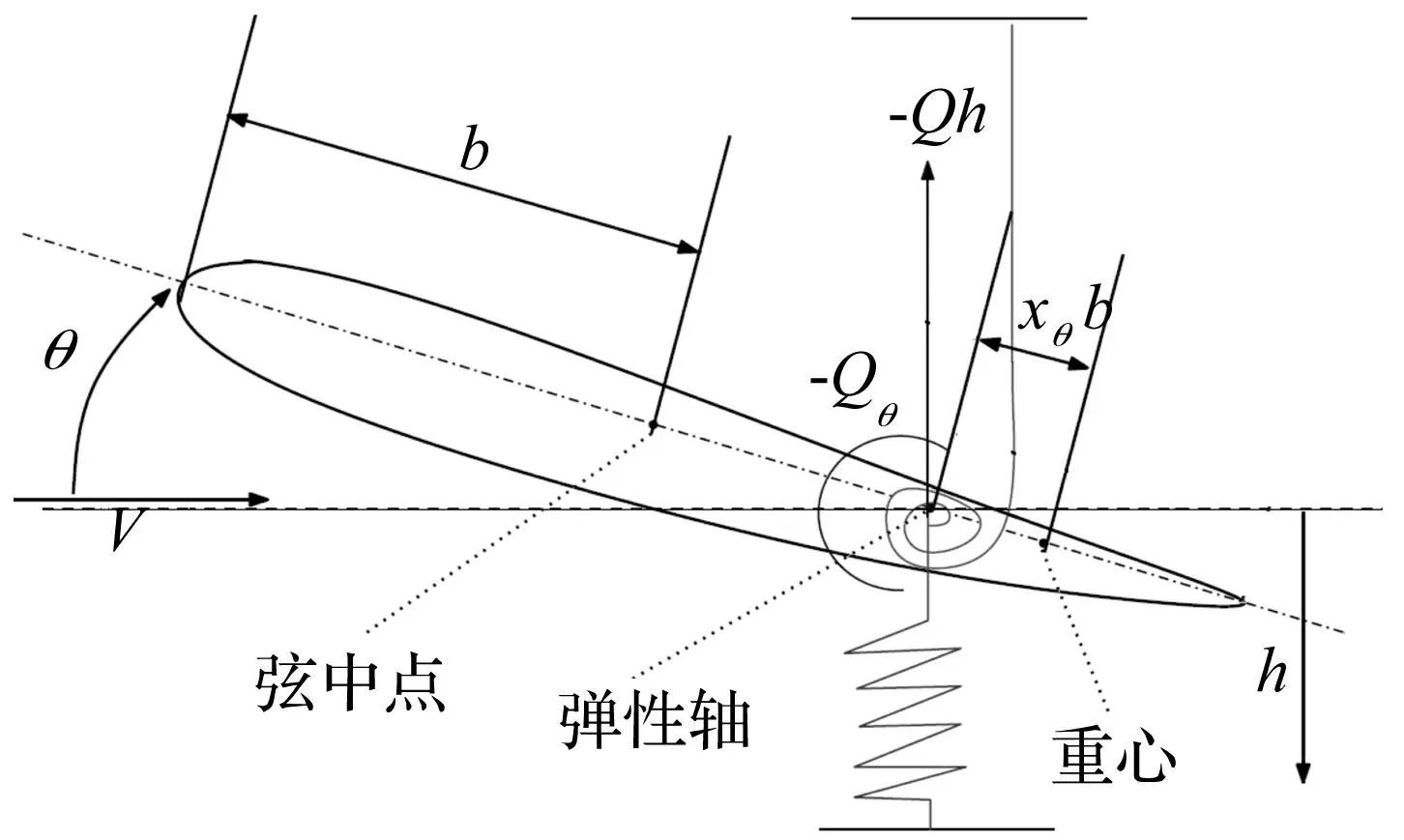
圖1　葉片截面結構模型Fig.1 The structural model of the blade section

1.2標量化振動方程

(3)

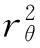
2Beddoes-Leishman氣動失速模型

2.1B-L非線性氣動失速模型

振動模型中的非定常氣動力由Beddoes-Leishman 氣動失速模型來提供。B-L模型可用于計算旋轉葉片氣動失速時的氣動負載。B-L非線性氣動失速模型的方程式為[10]：

(4)

式中前兩個方程式(x1,x2)為動態勢流特性，后兩個方程式(x3,x4)為動態氣流分離特性。x4=1表示完全附著流，x4=0為完全分離流。b1,b2,A1,A2分別為時間遲延和幅值常量。Tu,Tp,Tf為時間常量，有效攻角αE=α3/4(1-A1-A2)+x1+x2。由此為基礎非定常氣動力可表示為：

(5)

式中:CLdy為氣動升力系數，CMdy為氣動力矩系數，為了研究旋轉葉片處于失速狀態的系統氣彈穩定性，使葉片攻角周期性變化在大攻角范圍內，如[7° 13°],對應計算得到的旋轉葉片周期時變氣動升力(見圖2)。圖2可知攻角變化范圍位于深度失速區，發生了強烈的動態失速，渦流分離使得升力顯著上升高于靜態值，在氣流流動完全分離后，需要一定時間恢復到初始狀態。

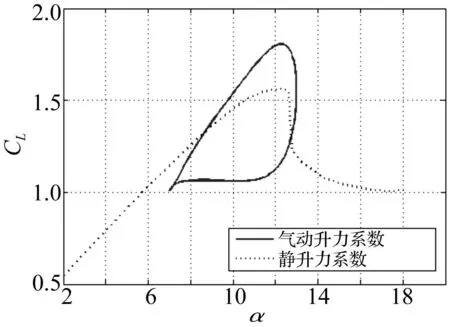
圖2　旋轉失速葉片非定常氣動升力Fig.2 Unsteady aerodynamic lift of the stall rotating blade

2.2氣動模型線性化

為了方便進行系統氣彈穩定性分析，需要將B-L非線性氣動模型線性化。假設氣動模型的狀態量可以表示為一個靜態項和一個動態項之和xi(t)=xi0+εxi1(t),i=1,2,3,4。泰勒級數展開所有的非線性項，得到線性化方程為[11]：

(6)

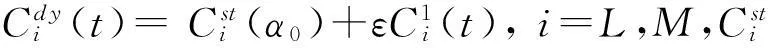
(7)

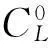
3Floquet理論

3.1旋轉葉片氣彈系統方程

結合振動方程式(3)和氣動方程式(6)、式(7)，可以得到旋轉葉片氣彈系統的方程。定義系統狀態量為：

氣彈系統狀態方程的同質部分可表示為：

(8)

式中：

(As, Bs) 來自振動模型的狀態方程式(3)，分別為振動模型狀態矩陣和輸入矩陣，(Aa(t), Ba(t), Ca(t), Da(t))為氣動失速模型的狀態方程矩陣式6)和式(7)。由于篇幅，就不在這里展開表述。由于風力機葉片周期旋轉，氣動力也跟著周期性變化，氣彈系統為周期時變系統，即A(t)=A(t+T),T為葉片旋轉周期。

3.2Floquet理論

Floquet理論用來分析周期時變系統的穩定性。對于時變系統，每個時間點對應的系統特征值已經不能夠代表系統的穩定性。Floquet理論的基本原理是通過建立Lyaponov-floquet轉換矩陣，將時變系統的狀態變換矩陣轉化為常量矩陣，以此來判定周期時變系統的穩定性。

文本中的旋轉葉片氣彈系統式(8)為周期時變系統，具有周期時間T。線性時變方程式(8)的解可以用狀態變換矩陣Φ(t,0)來表示[12]：

q(t)=Φ(t,0)q(0)

(9)

Floquet理論的本質就是將周期系統的狀態變換矩陣分解為一個周期時變矩陣和一個常量矩陣的指數函數形式：

(10)

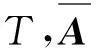
(1) Φ(0,0)=I,

(2) Φ(t2,t1)Φ(t1,t0)=Φ(t2,t0),

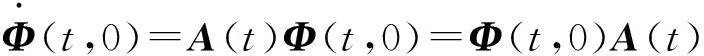
(4) P(0)=P(T)=I,

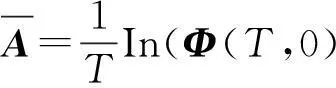
Φ(T,0)=VΣV-1,Σ=diag(σi)

(11)

(12)

由于P(t)是有界限的，系統q(t)的穩定性由A的特征值，即特征指數λi來判定。特征指數和特征乘數之間的關系如下：

(13)

由此可得到一個計算特征指數的方法：

ζi+jωi

(14)

式中：j2= -1，當σi為復數時，λi也為復數且有一對對應的共軛復數值。然而當σi為實數時，λi通常為復數但不一定會有共軛復數值。

3.3模型分析

將Floquet理論應用于系統模型分析包括三個步驟：

(1) 計算一個周期時間的狀態轉換矩陣Φ(T,0)

根據方程式(8)和方程式(9), 可以通過對下式進行積分得到狀態轉換矩陣：

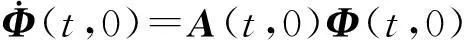
(15)

式中狀態轉換矩陣有線性獨立的初始值為Φ(0,0)=I，單位矩陣。

(2) 計算特征乘數σi

根據式(11), 通過對Φ(T,0)的特征值分析計算可以得到模型矩陣V和特征乘數矩陣∑。

(3) 計算每個特征指數中的實部(阻尼值)和虛部(頻率值)

根據式(14), 阻尼系數值可以表示為：

(16)

頻率值可以表示為：

(17)

系統模型的穩定性由特征指數中的阻尼值來判定：當ζi<0時，系統響應漸進穩定；當ζi=0時，系統響應臨界穩定；當ζi>0時，系統響應不穩定，此時ωi>0時 系統響應為不穩定震蕩，ωi=0時系統響應發散。

4數值分析

4.1特征指數分析和時域響應

本文中采用的結構參數為b=0.190 5 m,m=15.57 kg,xθ=0.192,μ=111.54,M=0.3,rθ=0.42[13]。給定揮舞/扭轉固有頻率ωh/ωθ=0.2, 結構阻尼ζh=ζθ=0, 應用floquet理論采用特征指數來分析系統的氣彈穩定性，并利用系統時域響應進行驗證。

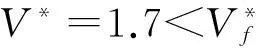
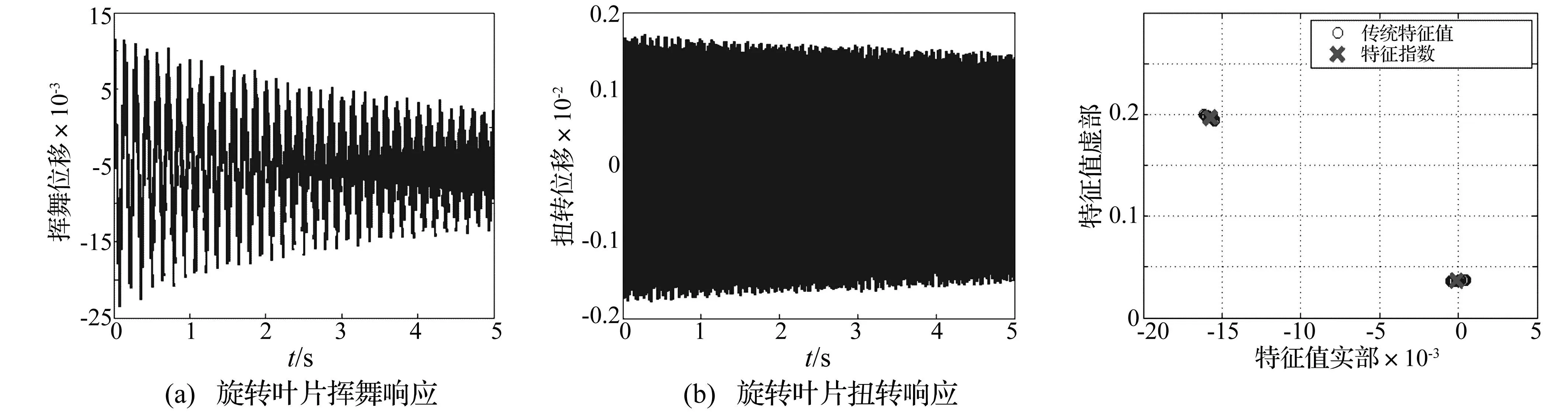
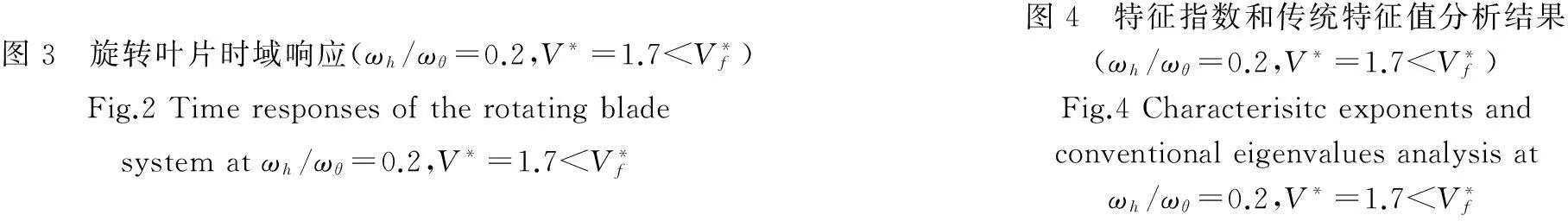
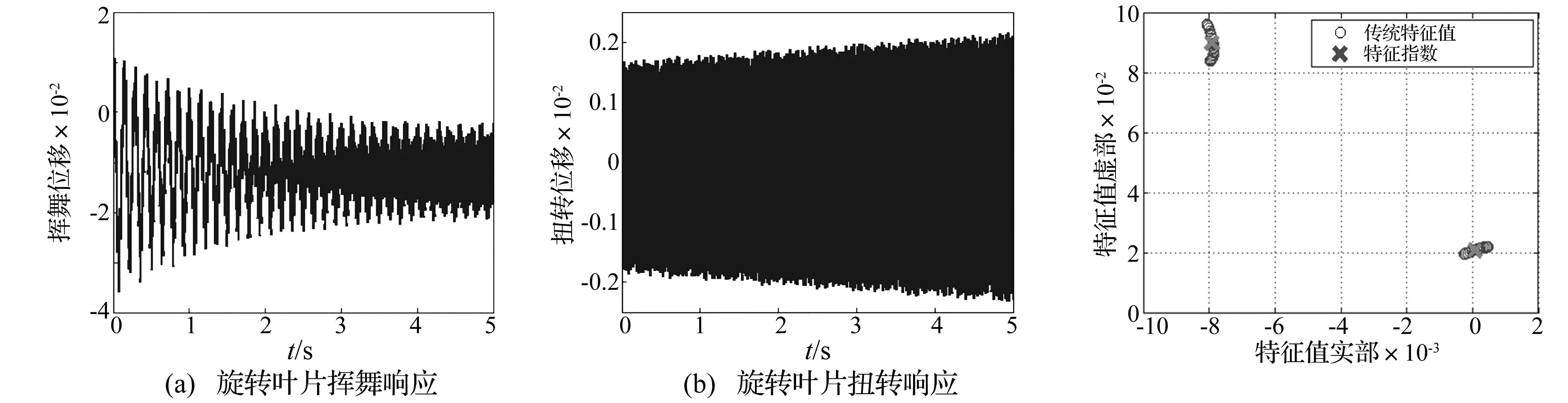
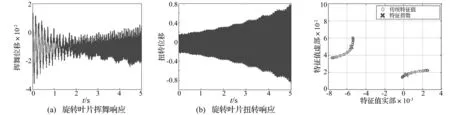
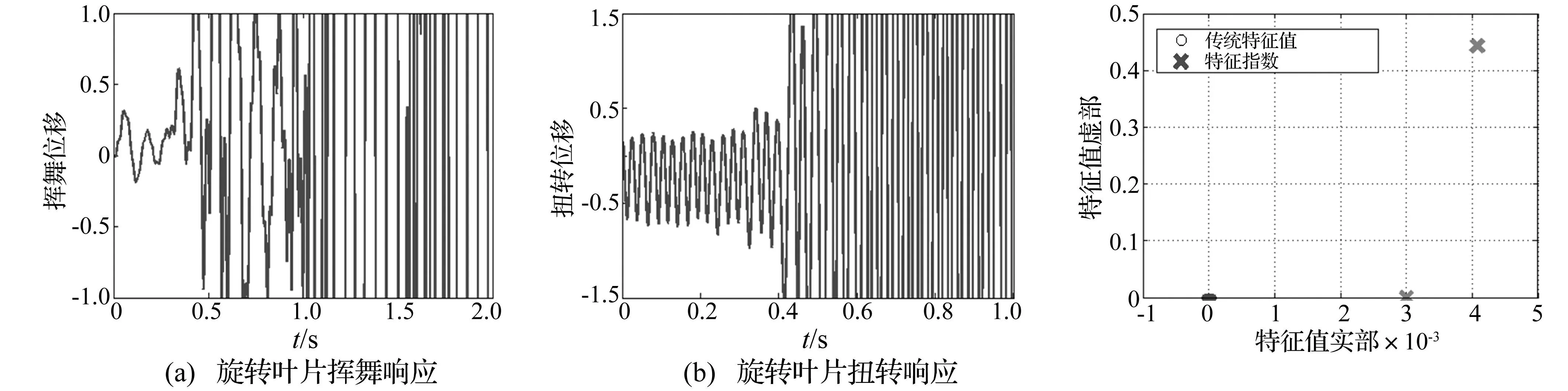
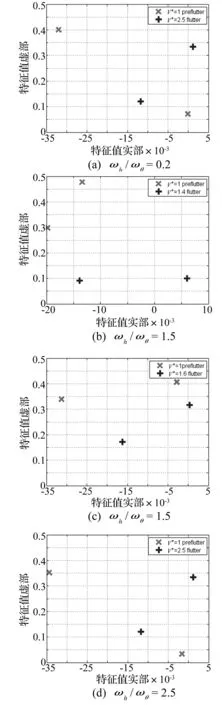
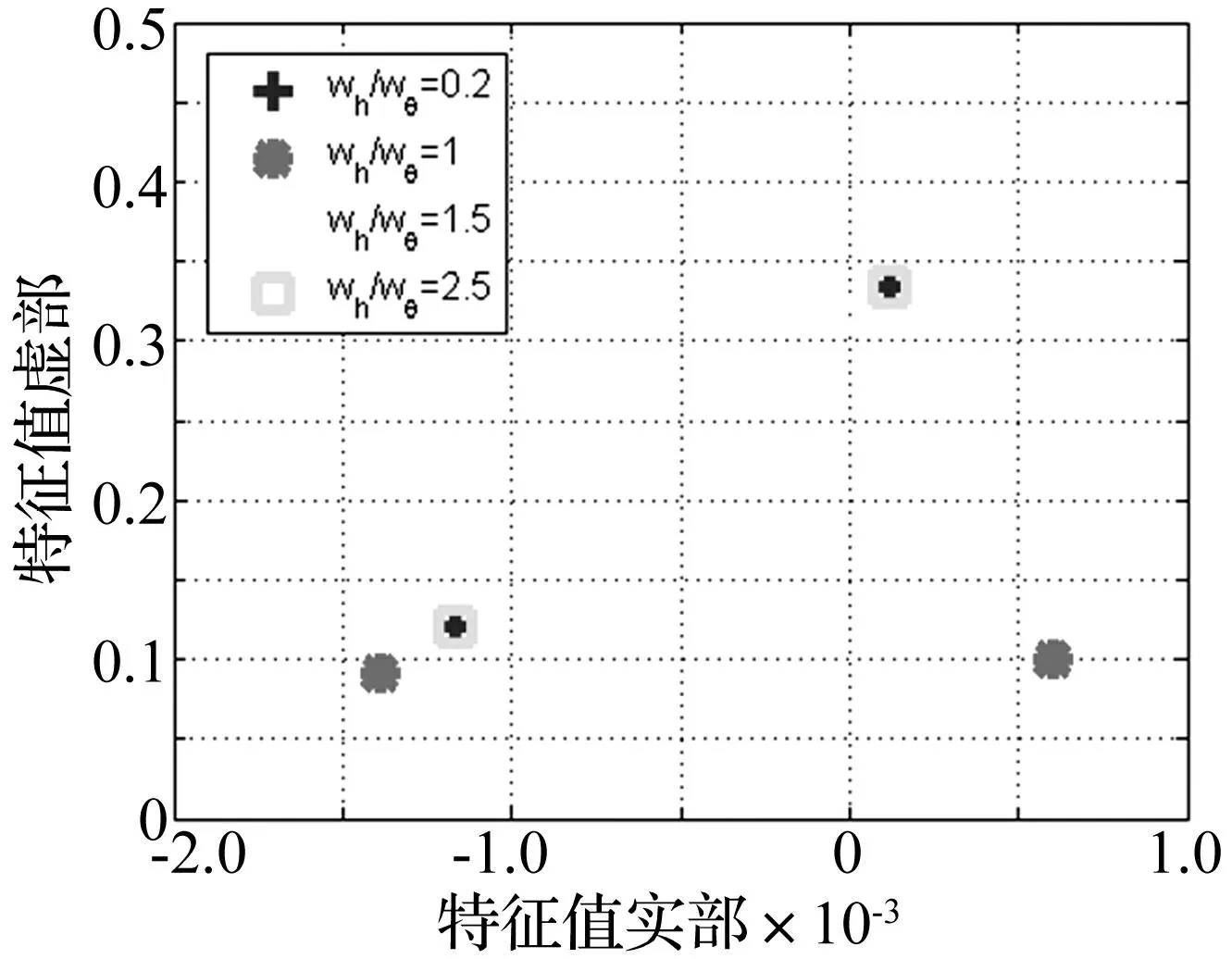
圖3 旋轉葉片時域響應(ωh/ωθ=0.2,V*=1.7

當到達顫振速度時，系統出現了不穩定顫振，此時特征指數出現了正實部如圖6所示。當V*增加到5時，系統時域響應進一步不穩定震蕩，特征指數同時進一步向右平面移動如圖8所示。當振后速度達到V*=16時，揮舞自由度的特征指數都在右半平面水平軸上，扭轉自由度的特征指數在右半平面內，表明系統發散不穩定；此時系統的時域響應在自由度最大變化范圍內發散，而傳統的特征值維持在零附近。

因此，旋轉葉片時變氣彈系統的穩定性無法通過傳統特征值來判定，而Floquet理論的特征指數可以準確地指示出系統的氣彈穩定性，其結果得到系統時域響應結果的驗證。

圖5 旋轉葉片時域響應(ωh/ωθ=0.2,V*=3.3=V*f)Fig.5Timeresponsesoftherotatingbladesystematωh/ωθ=0.2,V*=3.3=V*f圖6 特征指數和傳統特征值分析結果(ωh/ωθ=0.2,V*=3.3=V*f)Fig.6Characterisitcexponentsandconventionaleigenvaluesanalysisatωh/ωθ=0.2,V*=3.3=V*f

圖7 旋轉葉片時域響應(ωh/ωθ=0.2,V*=5>V*f)Fig.7Timeresponsesoftherotatingbladesystematωh/ωθ=0.2,V*=5>V*f圖8 特征指數和傳統特征值分析結果(ωh/ωθ=0.2,V*=5>V*fFig.8Characterisitcexponentsandconventionaleigenvaluesanalysisatωh/ωθ=0.2,V*=5>V*f

圖9 旋轉葉片時域響應(ωh/ωθ=0.2,V*=16>V*f)Fig.9Timeresponsesoftherotatingbladesystematωh/ωθ=0.2,V*=16>V*f圖10 特征指數和傳統特征值分析結果(ωh/ωθ=0.2,V*=16>V*f)Fig.10Characterisitcexponentsandconventionaleigenvaluesanalysisatωh/ωθ=0.2,V*=16>V*f

4.2揮舞/扭轉固有頻率比的影響

當其他參數保持不變，考慮固有頻率比的影響，圖11展示了4個不同揮舞/扭轉固有頻率比(分別為ωh/ωθ=0.2, 1, 1.5, 2.5)時，旋轉葉片的氣彈穩定性隨著標量風速的變化從漸進穩定過渡到顫振不穩定的變化過程。圖中采用特征指數來表示振前速度和顫振速度下的系統穩定性：不同固有頻率下，振前速度時的系統特征指數實部都在左半平面；顫振速度下的系統特征指數均有實部在右半平面。圖12展示了顫振速度下不同固有頻率比時系統的特征指數，表明在固有頻率比較低(ωh/ωθ=0.2)和較高(ωh/ωθ=2.5)時, 旋轉葉片的氣彈穩定性接近，而固有頻率比處于中間值(ωh/ωθ=1)時，系統有較大的正實部值，氣彈穩定性較差。

圖11　不同固有頻率比的特征指數(V*

4.3結構阻尼對顫振邊界的影響

在結構阻尼系數分別為ζh=ζθ=0，ζh=ζθ=0.001的情況下，旋轉葉片的顫振邊界(見圖13)。由圖13可知，在無結構阻尼的情況下，旋轉葉片氣彈系統在固有頻率比較低和較高時候有較高的顫振速度，在中間值1時有最小的顫振速度，表明在揮舞固有頻率和扭轉固有頻率相差較大時系統有較好的氣彈穩定性，在兩者固有頻率接近的時候系統有較差的氣彈穩定性。此結論與圖12的結論一致，得到驗證。在有結構阻尼的情況下，旋轉葉片的結構阻尼可以明顯提高在任意固有頻率比情況下的顫振速度，大大增強旋轉葉片的氣彈穩定性。

圖12　顫振速度下不同固有頻率比時的特征指數Fig.12 Characterisitc exponents at flutter speed for different ratio between flapwise and torsional natural frequency

圖13　不同結構阻尼下的顫振邊界Fig.13 Flutter boundary at different structure stiffness

5結論

本文將揮舞扭轉耦合的標量化葉片振動模型與非線性動力失速B-L模型相結合，提出了一個旋轉葉片時變氣彈系統，用以旋轉葉片的氣彈穩定性研究。B-L模型能夠較好的描述旋轉葉片的周期時變動態失速特性，采用Floquet理論分析旋轉葉片氣彈系統漸進穩定、顫振和發散等特性，并通過時域響應進行了驗證，表明了Floquet理論的可靠性和準確性。通過Floquet理論的特征指數計算結果揭示了旋轉葉片失速顫振邊界的特性以及結構阻尼對顫振邊界的影響。

參 考 文 獻

[1] Chaviaropoulos P K. Flap/lead lag aeroelastic stability of wind turbine blade section[J].Wind Energy,1999(2):99-112.

[2] Galvanetto U, Peiro J. An assessment of some effects of the nonsmoothness of the Leishman-Beddoes dynamic stall model on the nonlinear dynamics of a typical aerofoil section [J]. Journal of Fluids and Structures, 2008(24):151-163.

[3] 任勇生，林學海. 風力機葉片揮舞/擺振的動力失速非線性氣彈穩定性研究[J]. 振動與沖擊，2010，29(1):121-124.

REN Yong-sheng, LIN Xue-hai. Flap/lead-lag nonlinear aeroelastic stability of a wind turbine blade system during dynamic stall[J].Journal of Vibration and Shock,2010,29(1):121-124.

[4] 任勇生，劉廷瑞, 楊樹蓮. 風力機復合材料葉片的動力失速氣彈穩定性研究[J]. 機械工程學報，2011，47(12): 113-125．

REN Yong-sheng，LIU Ting-rui，YANG Shu-lian． Aeroelastic stability analysis of composite wind turbine blade dynamic stall[J]．Chinese Journal of Mechanical Engineering，2011，47(12): 113 -125．

[5] Leishman J G, Beddoes T S. A semi-empirical model for dynamic stall[J]. J. Am Helicopter Soc 1989, 34(3): 3-17.

[6] 劉廷瑞，任勇生，楊興華. 基于擬合氣彈系數的氣彈穩定性分析[J]. 太陽能學報，2010, 31(4):153-516.

LIU Ting-rui, REN Yong-sheng, YANG Xing-hua. Aeroelastic stability analysis based on fitted aerodynamic coefficients[J]. Acta Energiae Solaris Sinica, 2010, 31(4):153-516.

[7] 任勇生，張明輝. 水平軸風力機葉片的彎扭耦合氣彈穩定性研究[J]. 振動與沖擊，2010, 29(7): 196-200.

REN Yong-sheng, ZHANG Ming-hui. Aeroelastic stability of a horizontal axis wind turbine blade with bending-torsion coupled [J]. Journal of Vibration and Shock, 2010, 29(7): 196-200.

[8] 任勇生，杜向紅，楊樹蓮. 風力機復合材料柔性葉片的顫振分析[J]. 振動與沖擊，2011, 30(9):64-69.

REN Yong-sheng，DU Xiang-hong，YANG Shu-lian． Flutter analysis of composite flexible wind turbine blades[J]． Journal of Vibration and Shock，2011，30(9): 64-69．

[9] Mahajan A J, Kaza K R V. Semi-empirical model for prediction of unsteady forces on an airfoil with application to flutter [J], Journal of Fluids and Structures,1993(7):87-103.

[10] Hansen M H, Gaunaa M,Madsen H A. A Beddoes-Leishman Type dynamic stall model in state-space and indicial formulations [R]. Riso National Laboratory, Denmark, 2004.

[11] Kallesoe B S. A low-order model for analysing effects of blade fatigue load control [J]. Wind Energy, 2006(9):421-436.

[12] Balas, M J, Lee Y J. Controller design of linear periodic time-varying system[C]// Presented on Proceddings of the American Control Conference, Albuquerque, NM, USA, 1997(5): 2667-2671.

[13] Li N, Balas M J. Aeroelastic control of a wind turbine blade using microtabs based on UA97W300-I0 Airfoil[J]. Wind Engineering, 2013, 37(5): 501-516.

第一作者 李迺璐 女，博士，副教授，1985年9月生

摘要：研究旋轉風力機葉片動力失速氣彈穩定性問題。葉片結構采用標量化的揮舞和扭轉自由度耦合的振動運動模型，旋轉風機葉片的氣動力由Beddoes-Leishman失速模型來模擬，通過攻角在深度失速區域內的變化來計算出周期時變的非線性氣動失速負載。在系統靜平衡點附近對非線性氣彈系統進行線性化，采用Floquet理論分析旋轉葉片動力失速氣彈穩定性，其結果得到系統時域響的驗證。通過數值分析，揭示了揮舞扭轉固有頻率比和結構阻尼對顫振邊界的影響。

關鍵詞：旋轉風機葉片；氣動失速；Floquet理論；Beddoes-Leishman模型

Aeroelastic stability analysis on rotating stall blade of wind turbine based on floquet theory

LINai-lu1,MUAn-le2,BALASMJ2(1. Yangzhou University, Yangzhou 225127, China; 2. Xi’an Technology University, Xi’an 200215, China;3. Embry-Riddle Aeronautical University, FL 32114, USA)

Abstract:The aeroelastic stability of a rotating wind turbine blade under stall-induced vibration was studied. The blade structure was modelled as a normalized vibration system with a coupled motion between the two degrees of freedom of flapwise and torsional deflections. The periodic time-varying aerodynamic force on the rotating blade was determined by using the Beddoes-Leishman dynamic model via the computation of nonlinear aerodynamic stall load according to the variation of angle of attack in deep-stall range. Based on a linearized aeroelastic system, the aeroelastic stability of the rotating stall blade was analyzed in according with the Floquet theory, and the results were verified by comparing the system responses in time domain. It also reveals the effect of the ratio of flapwise to torsional natural frequencies and the structural damping on the flutter boundary.

Key words:rotating wind turbine blade; stall-induced vibration; Floquet theory; Beddoes-Leishman model

中圖分類號:TK83

文獻標志碼：A DOI:10.13465/j.cnki.jvs.2015.24.014

收稿日期：2014-08-12修改稿收到日期：2014-11-06

基金項目：江蘇省高校自然科學研究面上項目(14KJB480006);教育部留學回國人員科研啟動基金資助項目；揚州大學科技創新培育基金(2014CXJ028);國家自然科學基金(51075326);美國能源部項目(DESC0001261)