載荷辨識方法用于脈沖風洞模型阻力測量研究

王　鋒， 任　虎， 周　正， 賀　偉

(1.中國空氣動力研究與發展中心 吸氣式高超聲速技術研究中心，四川 綿陽　621000;2.中國空氣動力研究與發展中心 高超聲速沖壓發動機技術重點實驗室，四川 綿陽　621000)

?

載荷辨識方法用于脈沖風洞模型阻力測量研究

王鋒1,2， 任虎1,2， 周正1， 賀偉1

(1.中國空氣動力研究與發展中心 吸氣式高超聲速技術研究中心，四川 綿陽621000;2.中國空氣動力研究與發展中心 高超聲速沖壓發動機技術重點實驗室，四川 綿陽621000)

脈沖設備是進行高超聲速氣動問題研究的常用試驗設備，如激波風洞，其特點是有效試驗時間很短，在毫秒量級，為了在如此短的時間內對試驗模型的氣動力進行測量，澳大利亞昆士蘭大學的Sanderson等[1-4]設計了應力波天平，基于事先獲得的試驗系統脈沖響應函數和試驗中天平輸出信號，用反卷積方法辨識試驗模型在極短時間內所受氣動載荷，是最早將載荷辨識用于脈沖風洞模型測力的研究工作。本文所針對的風洞是一種特殊的脈沖式設備[5-6]，其有效試驗時間遠大于激波風洞，可達300 ms左右。此類設備由于試驗成本較低、試驗段口徑較大(目前最大直徑為2.4 m)，是目前國內開展超燃沖壓發動機和高超聲速飛行器性能研究的主力設備。對于質量不太大的試驗模型，通過適當提高天平的剛度，在300 ms左右的時間內，可以獲得有效的輸出信號，經低通濾波后，按照常規連續式風洞靜態測量的處理方法得到模型的氣動力[7- 8]。但隨著飛行器試驗模型的尺度和重量越來越大，為了在很短時間內得到有效的輸出信號，必須進一步提高天平力敏元件的剛度，以保證試驗系統的響應速度，這會降低天平的靈敏度和精度。未來的全尺寸試驗飛行器可能重達數噸，用現在的方法可能難以獲得滿意的測力結果，有必要研究將載荷辨識的方法用于此類風洞的模型測力。辨識的方法在理論上不需要系統響應達到穩態，因此可以適當降低天平力敏元件的剛度，提高其靈敏度和精度。不過，針對300 ms左右的時間，應力波天平是不適用的，而仍使用常規的應變天平，前者測量的是應力桿中的應力波引起的應變信號，后者測量的是系統結構振動在天平力敏元件上引起的應變。本文以簡單的鈍頭錐模型為對象，僅考慮單分量——阻力的測量，開展初步的方法研究，并進行試驗驗證，探索載荷辨識方法應用于脈沖燃燒風洞中模型測力的可行性。

1試驗系統設計

試驗模型是鋁制的鈍頭錐，半錐角22.5°，底部半徑125 mm，頭部半徑10 mm。

試驗所用天平是單分量測力天平，由超硬鋁整體加工而成，位于浮動框與固定框兩端的兩個薄板即為天平的力敏元件，其上下邊緣的中部粘貼4個應變片，構成惠斯通電橋。天平結構如圖1所示，(a)為俯視圖，(b)為對稱剖面圖。

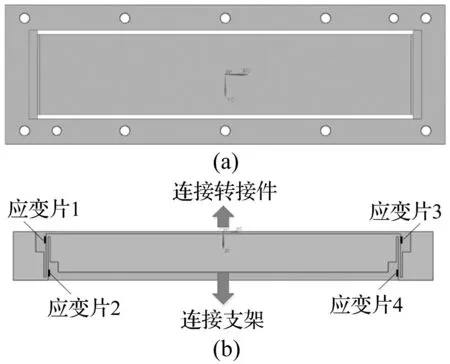
圖1　天平結構Fig.1 Structure of the balance

鈍頭錐模型通過一個鋼制的轉接件與天平的浮動框連接，天平的固定框與鋼制支座相連，支座下部固定于風洞內的地面。當鈍頭錐受到軸向載荷后，通過轉接件帶動天平浮動框產生位移，使力敏元件變形，通過應變片構成的電橋產生電壓輸出，實現測量。為了避免氣流作用于轉接件和天平，在模型后面用等直徑的圓筒作外罩來包覆轉接件和天平，外罩通過肋條固定于支座，外罩前端與鈍頭錐之間留有3 mm間隙，避免鈍頭錐在氣流作用下與外罩相碰。此外，為了使運動部分的質心位于天平的幾何中心，在轉接件后面加了配重塊。整個結構如圖2所示，(a)為側視圖，(b)為外罩內部結構。

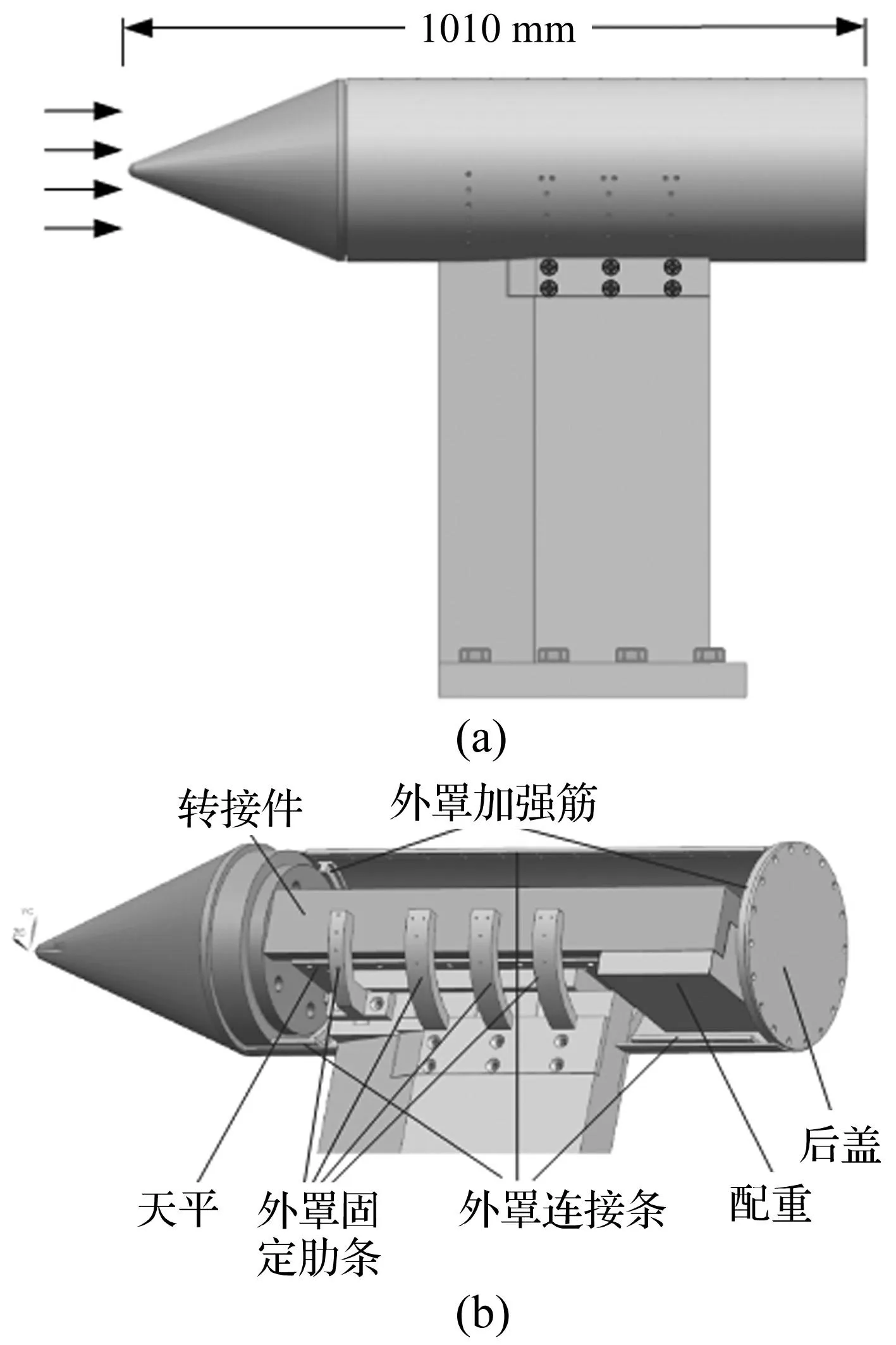
圖2　試驗系統組成Fig.2 Configuration of the test system

2試驗系統動力學模型

載荷辨識需要知道系統動力學特性，可以由微分方程、系統脈沖響應函數或傳遞函數來描述。

從系統結構可以看到，相對于天平的力敏元件(兩個薄板)，其它部分基本可看作剛性體。而作為力敏元件的矩形薄板在法向(面內拉伸)和側向(面內剪切)的剛度也遠高于軸向(彎曲變形)的剛度，因此，在僅受軸向載荷作用的情況下，試驗系統可近似建模為沿軸向的單自由度振動系統，其振動方程為

(1)

式中:x是模型沿軸向的位移，k是天平的等效剛度，f是軸向載荷，ξ為阻尼比，ωn為無阻尼圓頻率。在試驗中直接測量的系統響應是天平的輸出電壓v，其與模型的位移存在如下對應關系

v/Ks=kx

(2)

式中:Ks為天平的軸向靈敏度，單位mV/N，于是可將式(1)變為以天平輸出為變量的方程

(3)

式中：確定系統特性的參數就是ωn、ξ和Ks，下面通過動態標定來得到。

3試驗系統動態標定

動態標定是通過給系統施加已知的激勵，測量其動態輸出，據此辨識得到系統的動力學特性參數，實現系統的動力學建模，用于后續的載荷辨識。

系統的激勵通常采用階躍載荷或脈沖載荷[3]，在此采用前者。動態標定在脈沖燃燒風洞試驗現場進行，用細繩懸掛砝碼給系統施加軸向載荷，待穩定后突然剪斷細繩卸載，相當于給系統施加了一個反向的階躍載荷。試驗現場如圖3所示。

圖3　標定試驗現場Fig.3 Dynamic calibration setup

細繩的斷開過程需要一定的時間，假設在斷裂過程中繩子的拉力是線性變化的，則卸載過程近似為一個反向的斜坡階躍載荷。單位斜坡階躍函數如圖4所示，它本身含有一個參數，即上升時間τ，對應繩索的斷開過程。

圖4　單位斜坡階躍函數Fig.4 Unit ramp-step function

式(3)描述的系統在斜率為f/τ的斜坡載荷作用下的理論輸出[9]為

(4)

(5)

式(5)是加載過程的響應，對于卸載過程，相當于給加載后已處于穩態的系統施加一個反向的斜坡階躍載荷，其響應為

v(t)=vRstp(∞)-vRstp(t)

(6)

系統參數的辨識通過使理論輸出與動態標定的測量輸出之間的誤差平方和最小化得到，即求如下最小化問題的解

(7)

標定試驗共進行了3次，所加砝碼質量分別是10 kg、20 kg和40 kg，用三次試驗數據得到的參數辨識結果列于表1，系統參數ωn、ξ和Ks一致性很好，而第三次試驗的繩子斷開時間τ明顯大于前兩次，這是因為加載40 kg砝碼時用的繩子比前兩次的粗，所以其斷開時間更長。

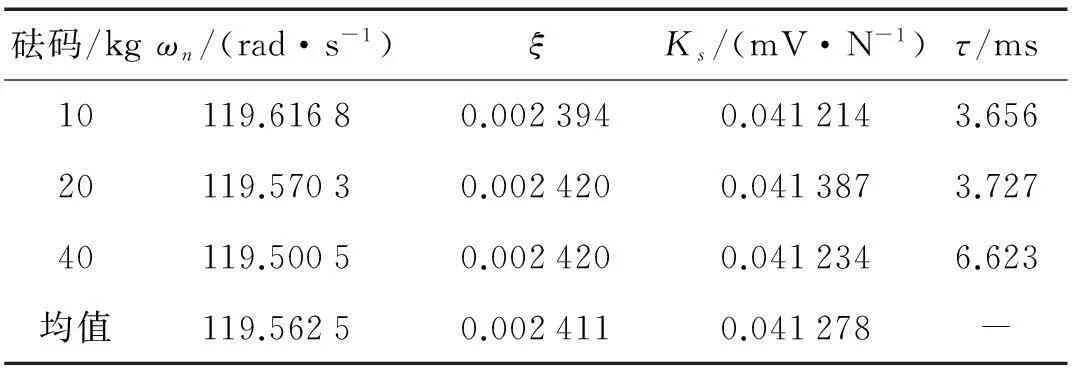
表1　系統參數辨識結果

用辨識得到的系統參數計算得到的理論響應與實測響應的對比如圖5，二者吻合很好，說明：第一，參數辨識結果是可靠的；第二，單自由度模型可以比較準確的描述系統。

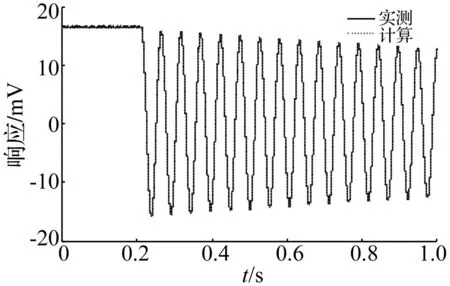
圖5　理論計算與實測響應對比Fig.5 Comparison between computed and measured responses

4模型阻力辨識

4.1載荷辨識方法

時域內的載荷辨識方法，通常首先將系統的動力學微分方程或卷積方程進行離散，建立待辨識時段上輸入輸出之間的線性關系方程[10]來求解。該方程一般是病態的，必須采取正則化處理，但在測量噪聲和模型誤差的影響下，獲得好的解并不容易。在此，我們采用載荷分解的方法，將問題轉化為一個函數參數辨識問題和一個低維的線性最小二乘問題。

根據脈沖燃燒風洞的工作特點[5-6]，在有效試驗時間內，模型所受載荷總體上應比較接近一個形狀如圖4所示斜坡階躍載荷，因此，用如下形式來近似模型的氣動載荷

(8)

即用一個斜坡階躍函數作為主要分量，用傅里葉級數逼近剩余分量。式中Rstp(*)代表斜坡階躍函數，其參數包括上升時間τ、幅值f和開始時刻t0，t0即氣流開始作用于模型的時刻，在此之前載荷為零，式中T為有效試驗時間。之所以不直接用傅里葉級數來近似整個載荷，是因為傅里葉級數逼近階躍型函數收斂較慢，通過用斜坡階躍函數將主分量分離出來，可以減少所需傅里葉級數的項數，避免用到高頻的三角函數，減小測量噪聲的影響。后面還會看到，斜坡階躍分量代表了試驗通常所關心的載荷均值。

根據線性系統的疊加原理，在式(8)所示F(t)作用下的輸出等于各分量載荷單獨作用下的輸出之和，將輸出記作vF(t)，則有

(9)

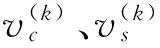
式(9)中τ、f、t0等參數對vF(t)的影響是非線性的，而ak的影響是線性的，在此采用兩步法分別來確定它們。首先令a0和ak、bk(k=1, …,N)取0，即假設模型僅受斜坡階躍載荷，通過求解如下優化問題

(10)

(11)

vr(ti)=a0vStep(ti-t0)+

(12)

對應n個采樣時刻，得n個這樣的方程，將未知系數分離出來，寫成矩陣形式有

ηr=Yα

(13)

(14)

最小二乘解一般不可能使方程精確滿足，因此依然存在逼近誤差，將其記作δ

(15)

用‖δ‖來表征誤差大小，其顯然與所取傅里葉級數的項數N有關，N取得越大，‖δ‖就可以越小。但是，由于測量本身存在噪聲，并且系統模型本身也存在因略去高階模態而引起的建模誤差，令‖δ‖越小所得到的載荷并不一定就越接近真實載荷，需要一個準則來確定最佳的N。

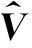
(16)

式中：頻率pL通過觀察輸出信號的頻譜來確定。

4.2仿真驗證

考慮系統的前兩階模態建立虛擬試驗系統，構造一個虛擬的載荷輸入，用計算的系統響應加上一定的噪聲模擬實測輸出，用來辨識輸入載荷，通過與已知輸入進行對比，對上述方法進行驗證。

虛擬載荷歷程取為帶隨機起伏的階躍狀曲線，如圖6中實線所示，其引起的輸出如圖7中的實線所示，其上疊加了方差為σ2=0.52的白噪聲。取截止頻率pL=30 Hz，相對誤差ε=0.001，載荷辨識結果如圖6中的點劃線所示，其中的斜坡階躍分量如其中的虛線所示。辨識載荷產生的輸出如圖7中的虛線所示。可見，斜坡階躍分量的幅值確實反映了載荷的均值，而辨識結果基本能夠復現真實載荷的大幅波動，只是對階躍處的快速變化載荷辨識精度不夠高，要提高該局部的辨識精度，可以通過對式(13)求加權最小二乘解來實現，具體不在此贅述。

現在考察測量噪聲對辨識結果的影響。定義辨識結果的相對誤差為

(17)

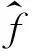
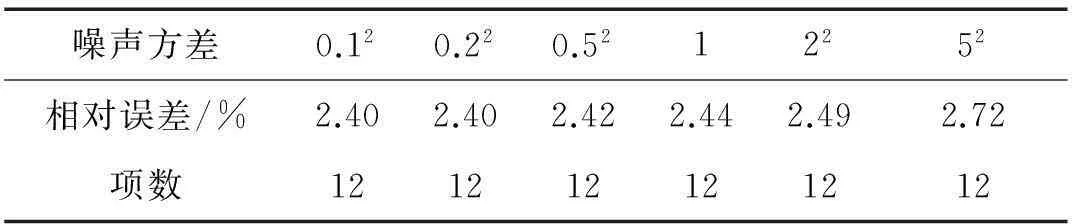
表2　測量噪聲的影響

現在考察系統參數誤差的影響。假設用來進行載荷辨識的系統數學模型的一階頻率和阻尼比與實際系統存在誤差，其定義如下

(18)

式中：x代表系統模型的頻率wn或阻尼比ξ，x0代表實際值。表3給出了頻率和阻尼比的獨立誤差對辨識結果的影響，可見頻率誤差對結果的影響很大，而阻尼比的誤差對辨識結果影響甚微。所以，通過動態標定來比較準確地獲取系統的參數十分必要。

表3　系統參數誤差的影響

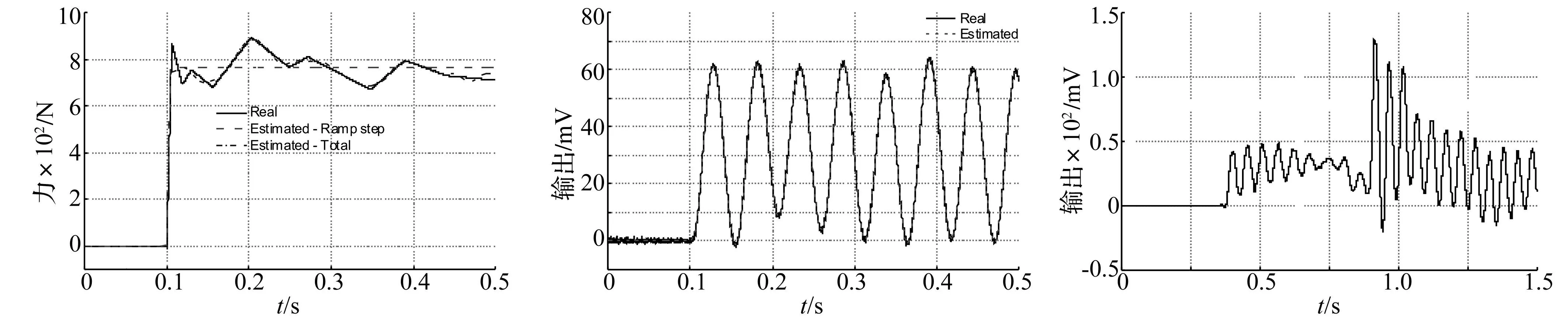
圖6 真實載荷與辨識結果對比Fig.6Comparisonbetweenrealandestimatedloads圖7 真實載荷與辨識載荷引起的輸出Fig.7Outputsbyrealloadandestimatedload圖8 第一車的天平輸出信號Fig.8Balanceoutputofthefirsttest

4.3試驗情況

吹風試驗共進行了兩車，由于實際配氣條件不完全相同以及每車所用膜片存在差異，兩次試驗的來流條件亦有所不同，測得的天平輸出信號分別如圖8、圖9所示。大約在0.75 s后，輸出開始異常，這是由于風洞擴壓段的氣流反射回來作用于模型所致，因此有效試驗段時間是0.75 s之前。

鈍頭錐模型的底部位于外罩之內，不直接受外流作用，但由于不是完全密封的，試驗時在內外壓差作用下會有氣流進入，導致模型底部壓力不斷升高，為了比較準確的計算模型的阻力，在外罩內部靠近模型尾部的地方放置了壓力傳感器來測量實際壓力，兩車的測量結果如圖10所示，取0.36s～0.75s間的數據作平均，分別是3.0 kPa和3.1 kPa，后面用于對CFD計算值作修正。

為了與辨識結果作比較，用CFD計算了鈍頭錐模型迎風面的阻力系數，參考面積取1 m2時，阻力系數CD為0.018 48。于是，在試驗穩定段模型的平均阻力計算如下

X=qCD-PbS

(19)

式中:q是來流動壓，Pb為模型底部平均壓力，S是模型底部面積。即使在有效試驗時段上，來流動壓也是波動的，并非期望的恒定值。但因為無法直接測量動壓的動態過程，只能根據配氣條件、燃燒室平均總壓測量值和風洞噴管參數計算給出試驗段的平均動壓。兩車的計算結果分別是50.118 kPa和51.534 kPa。這樣，式(19)給出兩車試驗中穩定段模型的平均阻力分別是778.92 N和800.18 N，將其視為模型實際阻力，用來考核用載荷辨識方法得到的結果。

4.4試驗載荷辨識結果

取0.3 s～0.75 s時段的數據來進行載荷辨識。首先對該時段上的天平輸出進行傅里葉變換，其幅頻曲線如圖11所示，信號主要能量分布在零頻和20 Hz左右，在此取截止頻率pL為30 Hz，取ε=0.001。

用4.1節的方法進行求解，兩車由式(16)所確定的傅里葉級數的項數N分別是12和13，計算得到的天平輸出與實測輸出的對比如圖12、圖13所示，二者的低頻特征吻合很好。

圖9 第二車的天平輸出信號Fig.9Balanceoutputofthesecondtest圖10 模型底部壓力測量曲線Fig.10Bottompressurevariation圖11 天平輸出的幅頻曲線Fig.11Amplitude-frequencycurveofthebalanceoutputs

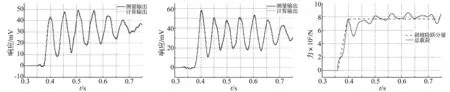
圖12 第一車的計算與實測輸出對比Fig.12Computedandmeasuredoutputsofthe1sttest圖13 第二車的計算與實測輸出對比Fig.13Computedandmeasuredoutputsofthe2ndtest圖14 第一車的載荷辨識結果Fig.14Identifiedforcehistoryof1sttest

兩車的載荷辨識結果分別如圖14、圖15所示，圖中虛線所示為式(8)中的斜坡階躍分量，實線為總載荷，可見，前者確實是載荷的主分量，而總載荷基本圍繞斜坡階躍分量波動，斜坡階躍分量的穩態值代表了模型載荷的平均值，因此用它與式(19)給出的預測值作比較，來評價載荷辨識的精度，結果列于表4，二者的差別在1%左右。從總載荷曲線看，第二車比第一車更平穩一些，這是因為第二車破膜過程快，來流動壓上升時間短，更接近階躍形式。另外發現，兩車載荷的起始時刻都比天平曲線上響應開始大幅上升的時刻要早，特別是第二車，在初始時刻載荷有個負170N的尖峰，這是由于在風洞啟動時有個較重的快速閥門開啟過程，造成較大沖擊，通過風洞基礎傳到支架引起天平輸出，圖12、圖13中3.5s時刻左右天平信號中的小幅波動即源于此，這可能導致初始時刻較大的載荷辨識誤差。

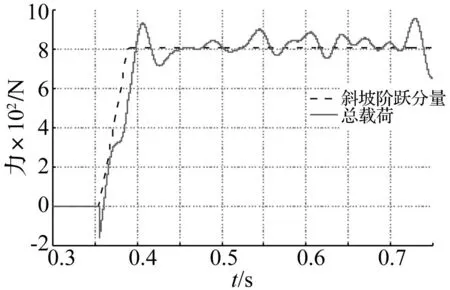
圖15　第二車的載荷辨識結果Fig.15 Identified force history of the 2nd test

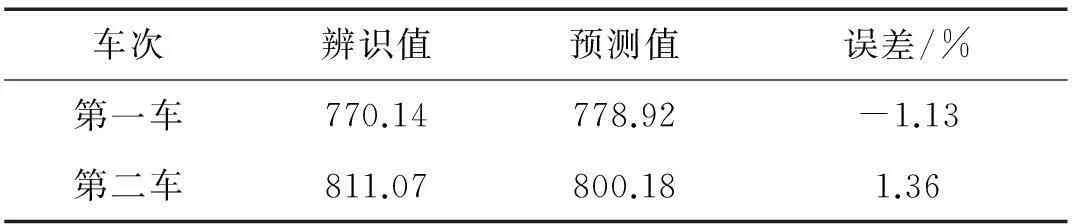
車次辨識值預測值誤差/%第一車770.14778.92-1.13第二車811.07800.181.36

5結論

本文以簡單的鈍頭錐模型為對象，用載荷辨識的方法取代常規的直接測力方法，以解決短時工作的脈沖型風洞中大質量模型的測力問題。用動態標定方法獲得了試驗系統結構動力學參數，建立了系統的簡化動力學模型。用斜坡階躍函數和傅里葉級數之和來近似模型的氣動載荷歷程，將載荷辨識問題轉化為函數參數辨識問題，采用分步求解方法，降低了求解難度，并提出了確定傅里葉級數項數的準則。針對試驗結果，利用此方法辨識得到了模型的阻力隨時間的變化曲線，與基于CFD計算和壓力測量給出的平均阻力預測結果吻合良好，二者偏差在1%左右。

限于風洞現有測量手段，沒有獲得吹風過程中來流動壓的動態變化數據，因此未能對動態載荷的辨識結果進行直接的驗證。將來需要進一步完善測量手段，在模型表面分布一定數量的測壓孔，用高精度的脈動壓力傳感器直接測量模型表面動態壓力，進而獲得模型的動態氣動載荷，而不僅僅是平均載荷，以便對辨識結果進行更細致的精度評估。

辨識方法得到的是隨時間變化的載荷歷程，這對于研究超燃發動機在點火啟動時的推力變化過程非常有用，而常規測力方法僅能通過低通濾波得到點火前后的穩態推阻特性[7-8]，難以較準確地反映啟動的瞬態過程。因此，新方法在吸氣式飛行器帶動力試驗研究中也有較大的應用價值。

參 考 文 獻

[1] Sanderson S R, Simmons J M. Drag balance for hypervelocity impulse facilities[J]. AIAA Journal,1991, 29(12): 2185-2191.

[2] Tuttle S L, Mee D J, Simmons J M. Drag measurements at Mach 5 using a stress wave force balance[J]. Experiments in Fluids,1995, 19: 336-341.

[3] Mee D J. Dynamic calibration of force balances for impulse hypersonic facilities[J]. Shock Waves,2003(12): 443-455.

[4] Robinson M J, Hannemann K, Schramm J M. Design and implementation of an internal stress wave force balance in a shock tunnel[J]. CEAS Space Journal, 2011(1): 45-57.

[5] 樂嘉陵，劉偉雄，賀偉，等. 脈沖燃燒風洞及其在火箭和超燃發動機研究中的應用[J]. 實驗流體力學,2005, 19(1): 1-10.

LE Jia-ling, LIU Wei-xiong, HE Wei, et al. Impulse combustion wind tunnel and its application in rocket and scramjet research[J]. Journal of Experiments in Fluid Mechanics, 2005, 19(1): 1-10.

[6] 劉偉雄，譚宇，毛雄兵，等. 一種新運行方式脈沖燃燒風洞研制及初步應用[J]. 實驗流體力學, 2007, 21(4): 59-64.

LIU Wei-xiong, TAN Yu, MAO Xiong-bing, et al. The development and preliminary application of a pulse combustion wind tunnel with new running way[J]. Journal of Experiments in Fluid Mechanics, 2007, 21(4): 59-64.

[7] 賀偉，童澤潤，李宏斌. 單模塊超燃發動機推力測量天平研制[J]. 航空動力學報,2010, 25(10): 2285-2289.

HE Wei, TONG Ze-run, LI Hong-bin. Investigation of thrust balance for the single module scramjet[J]. Journal of Aerospace Power, 2010, 25(10): 2285-2289.

[8] 賀偉，于時恩，李宏斌. 高超聲速一體化飛行器推阻特性測量研究[J]. 實驗流體力學,2010, 24(2): 65-68.

HE Wei, YU Shi-en, LI Hong-bin. Experimental investigation on thrust drag performance of hyper-sonic integrative vehicle[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(2): 65-68.

[9] Thorby D. Structural dynamics and vibration in practice: an engineering handbook[M]. Burlington: Elsevier Ltd, 2008: 53-55.

[10] 韓旭，劉杰，李偉杰，等. 時域內多源動態載荷的一種計算反求技術[J]. 力學學報,2009, 41(4): 595-602.

第一作者 王鋒 男，博士，副研究員，1976年6月生

摘要：對載荷辨識方法用于脈沖燃燒風洞模型阻力測量的可行性進行了研究。設計了鈍頭錐模型阻力測量試驗系統，通過突然卸載的方式對系統進行了動態標定，辨識得到了系統結構動力學參數，建立了系統動力學模型。基于脈沖風洞的工作特性，采用斜坡階躍函數與傅里葉級數之和描述模型的載荷歷程，將載荷辨識問題轉化為函數參數辨識問題，采取先辨識斜坡階躍函數參數再用最小二乘方法求傅里葉級數系數的求解策略。通過使理論計算輸出在低頻段逼近實測輸出來確定傅里葉級數的項數。首先通過數值仿真檢驗了方法的有效性，然后在脈沖燃燒風洞進行了兩車試驗，基于天平輸出對模型阻力進行了辨識，結果與CFD預測值吻合良好。

關鍵詞：脈沖風洞;阻力測量;動態標定;載荷辨識

Drag force measurement in impulse facilities by using load identification method

WANGFeng1,2,RENHu1,2,ZHOUZheng1,HEWei1(1. Air-breathing Hypersonic Technology Research Center, China Aerodynamics Research and Development Center, Mianyang 621000, China;2. Science and Technology on Scramjet Laboratory, China Aerodynamics Research and Development Center, Mianyang 621000, China)

Abstract:The feasibility of load identification method used in drag measurements on a model in impulse combustion facilities was discussed. A test system was designed to measure the drag force of a blunt cone model. The system was dynamically calibrated by sudden relief of a preload to excite the system. The dynamic parameters were estimated from the balance out, and a dynamic structural model of the system was established. A ramp-step function plus Fourier series were adopted to model the load history, and the force identification was transformed to the estimation of parameters of the function. A two-step solution skill was proposed, which estimates the parameters of the ramp-step function firstly, and then solves the Fourier coefficients by least square method. The term number of the Fourier series was determined by making the theoretical response approximating to the measured response at low frequency band. The method was validated by numerical simulations at first and then by two experiments in the impulse combustion tunnel. The drag forces of the cone model were identified from the measured balance output and the results agree well with the predictions by the CFD tool.

Key words:impulse facilities; drag measurement; dynamic calibration; load identification

中圖分類號:V231;O32

文獻標志碼：A DOI:10.13465/j.cnki.jvs.2015.24.034

收稿日期：2014-09-09修改稿收到日期：2014-11-19

基金項目：國家自然科學基金項目(11372339)；高超聲速沖壓發動機技術重點實驗室基金項目(STSKFKT2012001)