從解題的視角解密“一聽就懂，一做就錯”

張文虎　（河北省邢臺市第五中學　054000）

引導學生，通過已知結論尋求所要滿足的條件，通過逆向思維，證明這道幾何題目。

學生敘述時，教師可板書。

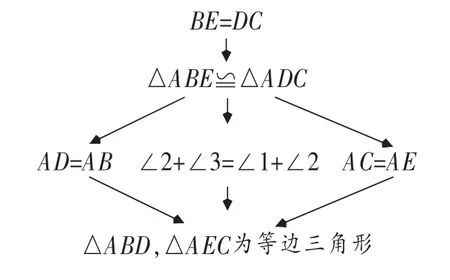
由此，學生便更加清晰地理解了此題的證明方法。

五、反證法

反證法是逆向思維在數學證明方法中的具體反應，反證法的實質是通過原命題的逆否命題的真實性來體現原命題的真實性，即通過提出假設后通過推理得到矛盾，從而證明結論的一種方法。這一方法擴展了學生的證明思路，并對培養學生的逆向思維能力有很大幫助。在反證法教學中，教師還應提醒學生注意反證法的適用情況及反證法在假設與推理過程中應該注意的問題，使學生形成縝密的數學思維習慣。

綜上所述，逆向思維的培養是一個長期的過程。在初中數學的教學過程中，教師應善于應用初中數學教材中的相關材料，注重在教學中培養學生的逆向思維能力。通過逆向思維能力的訓練，使學生獲得對數學知識更加全面的理解，完善學生的數學思維，并在今后的學習和生活中更加靈活地應用知識解決問題。

參考文獻：

楊昭（1991-），女，漢族，陜西咸陽人，陜西師范大學碩士研究生在讀,研究方向：課程與教學論。

[4]關文信.初中數學創新性教學指導[M].長春：吉林大學出版社，2001.

師：我們要證明BE=DC，需要怎樣考慮？先證明什么？

生：證明，△ABE=△ADC。

師：那么要證△ABE=△ADC，首先需要哪些條件？

生：AD=AB，∠2+∠3=∠1+∠2，AC=AE。

師：要證明AD=AB，∠2+∠3=∠1+∠2，AC=AE還需要什么條件？

生：△ABD，△AEC為等邊三角形（已知條件）

[1]王俊琴.數學教育……