對概念表述不規范的案例分析和思考

李偉

[摘 要]課堂教學中，如果教師對概念的理解不到位，導致表述不規范，甚至出現錯誤，會嚴重影響學生的后續學習。所以，教師不僅要加強理論學習，提高自己的素養，還要提高自身的業務素質，打造過硬的基本功。

[關鍵詞]概念 表述 平移 旋轉 正比例 反比例

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2016）01-023

經過近幾年的調研，我發現課堂教學中，如果教師對知識性概念表述不規范，甚至出現錯誤，會使學生被動接受缺失的知識，從而導致課堂教學效率低下。為了避免這種現象的發生，現我把課堂教學中出現的個別案例進行分析與思考，并采取相應的教學對策，使學生真正理解所學知識。

一、課堂教學中個別案例的分析與思考

案例1：角的概念及畫法的迷茫

【課堂掃描】

（1）對角的初步感知。

師：摸一摸三角板中的角，有什么感覺？

生1：尖尖的、扎扎的。

生2：刺手。

師：這尖尖的、扎扎的就是角。你能舉出生活中看到的角嗎？

生3：紅領巾中有角。

生4：牛角。

生5：墻角。

生6：桌角。

……

（2）角的畫法。

（師示范角的畫法，如下圖）

……

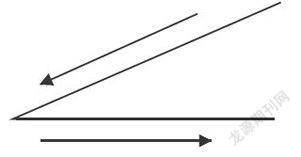
分析與思考：

數學知識具有高度的抽象性，而小學生往往只有通過操作獲得直接的經驗，才能在此基礎上進行正確的抽象和概括，形成數學的概念和法則。因此，教師可根據學生學習的這一特點，通過實際操作活動來幫助學生認識角，即從實物中抽象出所學的角，使學生經歷抽象的過程，感受到數學知識的現實性，學會從數學的角度去觀察，然后讓學生說說這些都是什么，初步感知角。這一教學環節符合課程改革的要求，教師引導學生建立角的直觀認識的過程也清楚，但學生對角的概念認識不到位，認為桌角、牛角、墻角等都是角。其實，這些角是生活中的角，與數學上的角不是同一概念，因為我們研究的角是從無數實物中抽象出共性后形成的概念，即物體上的角是指物體面上的角，我們研究的是平面圖形，是二維空間的角，而桌角、墻角等屬于三維空間。所以，教師應該及時從物體上抽象出平面圖形，告訴學生角是平面圖形，角有一個頂點、兩條邊，且邊是直直的，不能說成角是尖尖的、扎扎的、刺手的。

客觀世界中并不存在平面圖形，只有立體圖形，因此兩千多年前的泰勒斯、歐幾里得確定了角的概念和表示方法，時至今日我們后人理應用知識繼承的方式來學習角的知識。如角的畫法，教師應告訴學生：“從一個點起，用尺子向不同的方向畫兩條線，就畫成一個角。”而有個別教師如上圖所示畫角，錯因是畫了一條射線，但另一條邊不是按射線的定義畫的，這和角的概念“從一點引出兩條射線就組成一個角”不符，給以后的教學帶來不便。建議教師在教學中示范角的畫法時必須是科學的、規范的，因為概念學習先入為主，一旦形成思維定式，再進行糾正就難上加難了。所以，教師對概念內涵和外延的理解要準確無誤，這樣才能傳授給學生正確的知識。

案例2：對平移和旋轉的認識不到位

【課堂掃描】

師：除了課本上介紹的平移外，生活中你還見過哪些平移現象？

生1：算珠的移動。

生2：雜技運動員在舞臺上騎自行車時的表演。

生3：火車的運動。

……

師：同學們舉的例子都很好。

……

師：除了課本上介紹的旋轉外，你還能舉出生活中哪些旋轉現象？

生4：風扇的轉動。

生5：雜技運動員在舞臺上騎自行車時的表演。

生6：繩子的一端系著小球，另一端用手旋轉。

生7：“神舟七號”的發射和地球的自轉。

……

分析與思考：

平移和旋轉都是物體運動的方式，教師教學時從生活實例引入，通過直觀形象的圖示，引導學生了解什么樣的現象是平移、什么樣的現象是旋轉，使學生從中感知和體會到這兩種運動方式的不同，從而形成比較清晰的知識表象。教學中，學生對平移和旋轉這兩個概念說得不到位的地方，教師要注意及時給予點撥、引導。如果教師不進行引導和評價，會給學生的后續學習帶來錯誤，甚至出現知識缺失的遺憾。

課堂教學中，對于物體進行平移運動，教師要引導學生注意兩個參量：一是物體本身的方向不能改變，即要沿直線運動;二是移動的距離，即圖形中每個點的平移距離要相等。如雜技運動員在舞臺上騎自行車時的表演是轉圈，雖然是按順時針或逆時針轉，但沒沿直線運動，故不能視為平移;現實生活中火車的行駛是拐彎的，顯然也不能說是平移，建議教師教學時以圖片的形式呈現火車行駛的路線（軌道是直的），或說明火車在某一時間段沿直線運動，這樣表述火車運動時車身的移動是平移的才準確無誤。

對于物體進行旋轉運動，教師同樣要引導學生注意兩個參量：一是要圍繞一個點或一條軸運動;二是作等角度的圓周運動。根據這兩個參量，雜技運動員在舞臺上表演騎自行車的運動顯然不是每一圈的大小都相等，轉的角度也有差別，故不能視為旋轉。這時，教師可加以點撥：“假設雜技運動員在同一個圓周上轉圈的話，則可以看做是旋轉;繩子的一端系上小球，另一端用手旋轉，這一例子在現實中由于手不固定，即沒有固定點，也不能視為旋轉。同樣，‘神舟七號’的發射，它的運動分為幾個階段，開始從地面直線上升是平移，經過一段時間后進入軌道運動，進入軌道后是等圓周運動，則為旋轉，而直線運動后到進入軌道前這一段的運動則既不是平移也不是旋轉，因為它既不是沿直線運動，也不是進行等角度運動。”這里，建議教師強調“神舟七號”進入軌道后才是旋轉。另外，地球的自傳是旋轉的表述也不規范，因為地球是橢圓體，沒作等角度運動。以上例子中的平移和旋轉，實際意義上都不符合概念，且描述不規范，甚至出現知識性錯誤，所以我們要引起高度重視，因為數學講究的是嚴謹。

案例3：正反比例的判斷有誤

【課堂掃描】

師：判斷下列說法是否正確，并說明理由。

出示題目：買《小學生數學報》的總價錢一定，所以買《小學生數學報》的份數和單價成反比例。

生1：正確。因為買《小學生數學報》的總價錢一定，買《小學生數學報》的份數和單價的積就一定，根據積一定，所以買《小學生數學報》的份數和單價成反比例。

師：回答得很好。

（此時，還有不同意見的學生聽到老師的評價后，盡管滿臉疑惑，但還是慢慢地把手放了下去）

……

分析與思考：

正反比例的意義比較抽象，它們都表示兩個相關聯變量之間的一種數學模型。無論是正比例還是反比例，它們都有三種參量，即兩種量相關聯、一種量隨著另一種量變化、比值或積一定。這三種參量要同時具備，才能判定兩種量是否成正比例還是成反比例，但這里要特別注意的是必須有兩種變量才行。如上述教學，學生的判斷雖然符合兩種量（買《小學生數學報》的份數和單價）相關聯且積一定的條件，但這里隱含著一種不易被發現的常量——《小學生數學報》的單價。現實生活中，《小學生數學報》的價錢已定，短時間內不會改變，這是不爭的事實。既然《小學生數學報》的單價一定，總價錢又一定，可推斷出《小學生數學報》的份數也一定，這樣三種量都不變，都成了常量。這和反比例中必須有兩個變量和一個常量相違背，顯然不符合反比例的意義，故此命題不成立。也許教師的出發點是想讓其成反比例，但忽略了《小學生數學報》的單價是定值。課后和這位教師交談時，她仍然堅持自己的意見，對此我征求了十幾位教師的意見，他們都給出了相似的回答。如下：

師1：這個命題不嚴謹，不應該出，因為《小學生數學報》的單價一定，這樣三個量都沒有變量了，也就不成反比例了。

師2：這個命題不嚴密，考慮問題不全面，判斷成反比例不合適。

師3：考慮問題不全面，可能成反比例，也可能不成比例，有爭議的題不應該出。

師4：這個命題作為判斷題不合適，最好不出。

師5：這個命題不嚴密，甚至是錯誤的。

……

最后，我又請教了中央教科所的李嘉駿老師，李老師說：“現實中《小學生數學報》的單價已定，故此種命題的設計欠嚴謹，甚至有誤。”

二、教學對策

經過調查了解得知：課堂教學中出現知識性問題的教師，有的是剛畢業的教師，有的是農村教師。針對現狀，為了避免今后在課堂教學中出現類似知識性的問題，建議教師們：第一，不僅要加強理論學習，提高自己的素養，還要提高自身的業務素質，打造過硬的基本功，做終身學習的教師。第二，要吃透教材，活用教材。教師要掌握教材、用活教材，因為教材是教學的載體，所以我們要用教材教，而不是教教材，要將教材為自己所用，而不是被教材所束縛。因此，教師備課時，首先要理解知識，明確教材的重、難點及關鍵處;其次，要掌握教材各部分知識的來龍去脈，以及教材中主題圖、情景圖、例題和習題等的編寫意圖。只有細心鉆研，做到胸中有書，才能解決“教什么”的問題。同時，教師只有在吃透教材的前提下才能統觀全局，掌握知識的系統性;只有在教的基礎上才更注重研究，思維才更嚴謹、完整，知識的內涵和外延才能理解得深刻和透徹，才能避免知識性問題的發生。

（責編 藍 天）